PM2.5的相关因素时间序列分析模型

王来斌

一、引言

我国华北的部分城市每年冬天都会遭遇雾霾的多次袭击。许多人的日常上班，学习都受到影响，当雾霾天气中细微颗粒物浓度很高时，环境污染会对人体造成严重的不良影响，比如呼吸道感染，心脑血管疾病，心肺疾病等发生比率上升。PM2.5也被称为细微颗粒物，是指大气中直径小于等于2.5微米的悬浮颗粒物。PM2.5粒子直徑小，易于富集空气中的有毒有害物质。

由上文所述背景，本文就是对PM2.5浓度的气象影响因素进行分析建模，并预测未来一段时间的PM2.5浓度，尽可能准确地做出预报，为人们的日常工作学习提供参考和依据，降低PM2.5带来的空气污染所造成的损失。本文基于UCI上记载的北京市2010-2015年每日12时的PM2.5监测值，运用机器学习相关算法预测未来一段时间的PM2.5预测值。

二、ARIMA模型的建立

（一）建立ARIMA模型

1.时间序列图

时间序列图分析模型能进行精度比较高的短期预测，因此针对北京市东四2015.1.1-2015.12.21共355天的数据用R软件进行建模预测。由结果图可知，北京东四在2015.1.1-2015.12.21的PM2.5值并不平稳，故要进行变换或者差分处理。

对原始数据进行一阶差分，差分后的值显示平稳但是还需要进行单位根检验。一阶差分图如图1

2.单位根检验

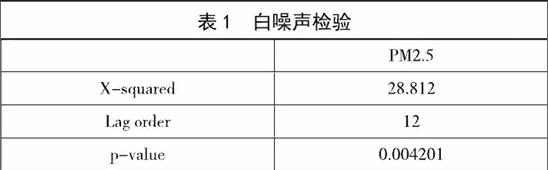
单位根检验的P值小于0.05，故拒绝原假设，为平稳序列。接下来进行一阶差分后的白噪声检验

滞后12阶指标相关统计量如下表所示。

我们可以看出，两个指标取对之后进行差分过后均显著，是非白噪声序列，我们可以进行接下来的模型识别和模型选择。

3.模型识别及定阶

通过R软件中的自动定阶，得出最合适的模型是ARMA（1，4），因为进行了一阶差分，故最终模型为ARIMA（1，1，4），如下：

ARIMA（1，0，4） with zero mean ： 4052.331

Best model： ARIMA（1，0，4） with zero mean

Series： X3

ARIMA（1，0，4） with zero mean

Coefficients：

ar1 ma1 ma2 ma3 ma4

-0.1322 -0.3429 -0.3689 -0.1963 -0.0667

s.e. 0.5663 0.5635 0.2787 0.1864 0.1110

sigma^2 estimated as 5687： log likelihood=-2020.04

AIC=4052.09 AICc=4052.33 BIC=4075.27

5.模型的诊断

Q-Q图来检验残差的正态性：

Q—Q图是一种有效平谷正态性的工具，由图可知整体趋势接近一条直线，但是也存在异常值。但总体上是正态的。

6.模型的预测

建立好模型之后，我们需要对于模型进行预测，R软件的时间序列功能能帮助我们针对有效的模型进行良好预测。根据PM2.5初始值，我们对于2015.12.22.-2015.12.31共10天数据预测，预测值分别是：168.3501 126.8469 110.9921 109.3322 110.1681 109.7472 109.9591 109.8524 109.9061 109.8791 而实际值分别为：138.00 127.00 106.00 102.63 106.00 116.00 111.00 102.00 115.00 110.00

可以看出与实际值差别不大，说明预测的较为准确。

五、总结

本文综合运用了多元回归分析、主成分分析对PM2.5的相关因素进行了统计上的分析，又利用ARIMA时间序列分析对PM2.5质量浓度进行预测。ARIMA模型较好的解决了大气中PM2.5的时间分布问题，具有良好的预测效果。endprint