基于TQWT的癫痫脑电信号的识别*

贺王鹏，杨琳，王芳，黄绍平

（1.西安电子科技大学空间科学与技术学院，西安 710071；2.西安交通大学第二附属医院，西安 710004）

1 引 言

癫痫是大脑神经元突发性异常放电，导致短暂的大脑功能障碍的一种慢性疾病，其反复发作，严重影响了患者的日常生活和工作［1］。利用脑电图（EEG）可以记录到癫痫发作时的异常电活动，具体表现为高幅同步节律波，主要包括棘波、尖波、棘-慢复合波、尖-慢复合波和多棘波等癫痫特征波形［2］。然而，长时间的EEG记录会产生大量的数据，医生人为的视觉检测效率较低且非常耗时，并且长时间的观察EEG会增加医生的疲劳度进而影响其判断力和诊断结果的准确性。因此，研究癫痫脑电信号的自动检测与识别技术具有重要的意义［3］。

EEG信号具有非平稳的特点，并且在采集过程中受到多种噪声成分的干扰，对其进行分析需要利用先进的信号处理方法。近年来，研究人员提出了多种不同的癫痫EEG信号特征提取和分类的方法，主要包括：时域统计方法、频域分析方法、短时傅里叶变换、小波变换、经验模式分解、人工神经网络、支持向量机（support vector machine，SVM）等［4］。其中，小波变换具有良好的多分辨特性并拥有丰富的基函数，使得其在非平稳信号处理、动态信号降噪等应用方面展现出明显的优势，并在EEG信号处理中取得了显著的成就［5］。然而，传统离散小波变换的小波基函数的品质因子Q（中心频率和带宽的比值）是固定的，难以根据待分析信号的振荡特征进行灵活的匹配。2011年，纽约大学的Selesnick教授提出了一种在频域中构造新的过完备小波变换，即可调品质因子小波变换（tunable q-factor wavelet transform，TQWT）。TQWT理论的出现解决了小波的Q不能调节的问题［6］。该小波可灵活的调节小波基函数的Q，使小波的振荡特性与特征波形的振荡特性相匹配［7］。

本研究针对癫痫EEG信号的自动检测与识别难题，提出了一种基于TQWT的癫痫EEG信号自适应分析与识别方法。首先，利用灵活的TQWT对EEG信号进行分解，得到各个小波子波带；然后，根据癫痫异常波对应的频率范围自适应的选择相应小波子波带进行重构，并提取有效值和峰峰值构成特征分量；最后，采用SVM进行癫痫EEG信号的分类识别。将所提出方法应用于癫痫EEG信号的自动识别中，以德国伯恩大学癫痫研究中心采集的典型脑电数据进行验证。实验分析结果表明，所提出的特征提取方法对正常和癫痫发作期EEG信号的分类准确率可达98%，验证了方法的有效性。

2 癫痫EEG信号提取与分类方法

2.1 可调品质因子小波变换（TQWT）

为克服传统离散小波变换存在的不足，Selesnick于2011年提出了可调品质因子小波变换（TQWT）。TQWT是在频域进行构造，在频域上完成小波基的设计及其张成多尺度空间的划分网格，能够有效地解决小波基时域振荡特性的调节问题。TQWT是一种结构化的设计方法，通过参数化设置可以决定小波基的全部性质。TQWT的执行滤波器组与离散小波变换相似，采用迭代的双通道滤波器结构，其滤波器组原型见图1。其中LPS和HPS分别代表低通尺度伸缩和高通尺度伸缩，尺度参数分别为α和β。

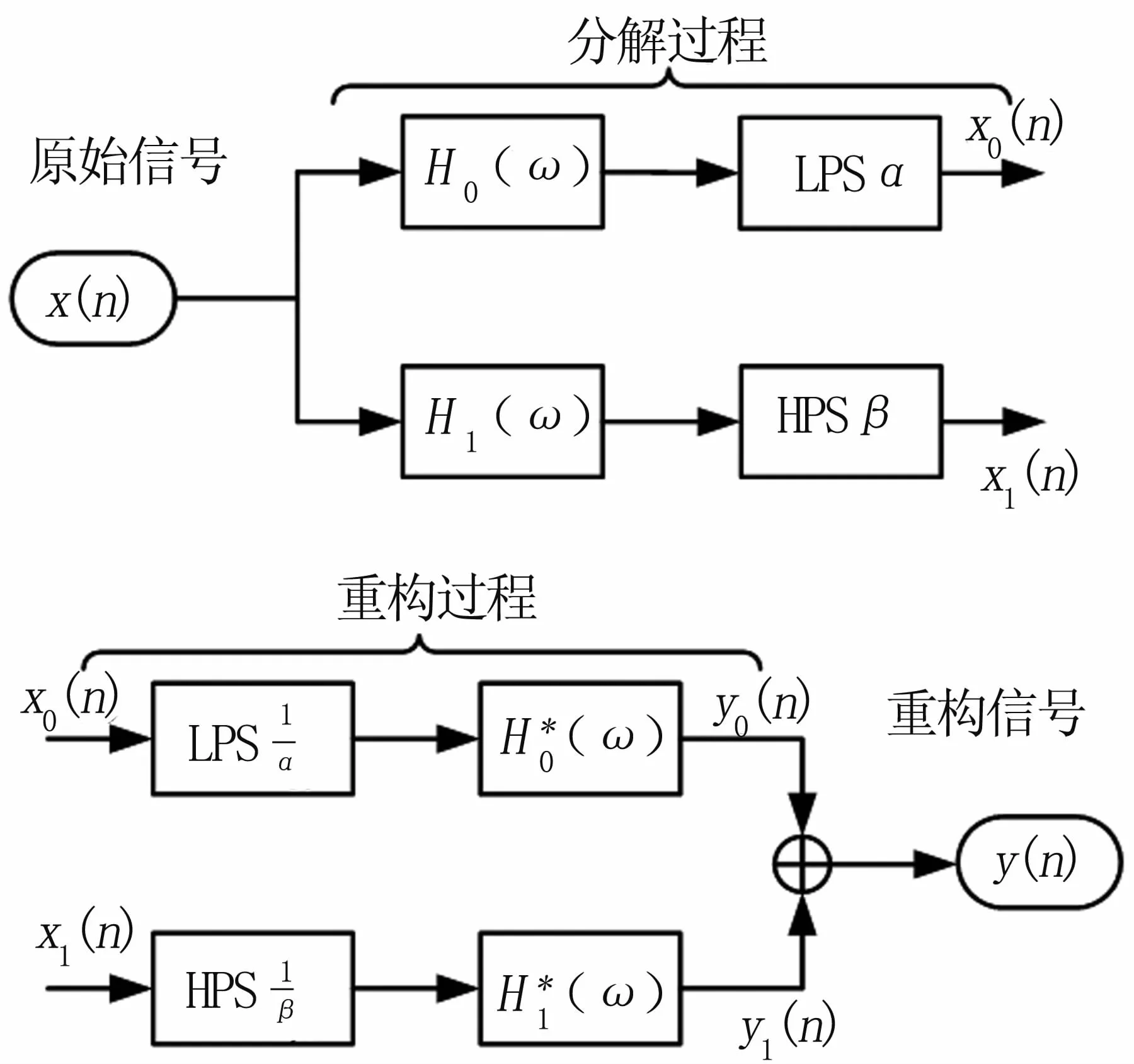
图1 TQWT分解与重构过程示意图Fig 1 Block diagram of decomposition and reconstruction for the implementation of the TQWT

为实现TQWT的完美重构，TQWT中低通滤波器和高通滤波器的频率响应H0（ω）和H1（ω）分别设计为：

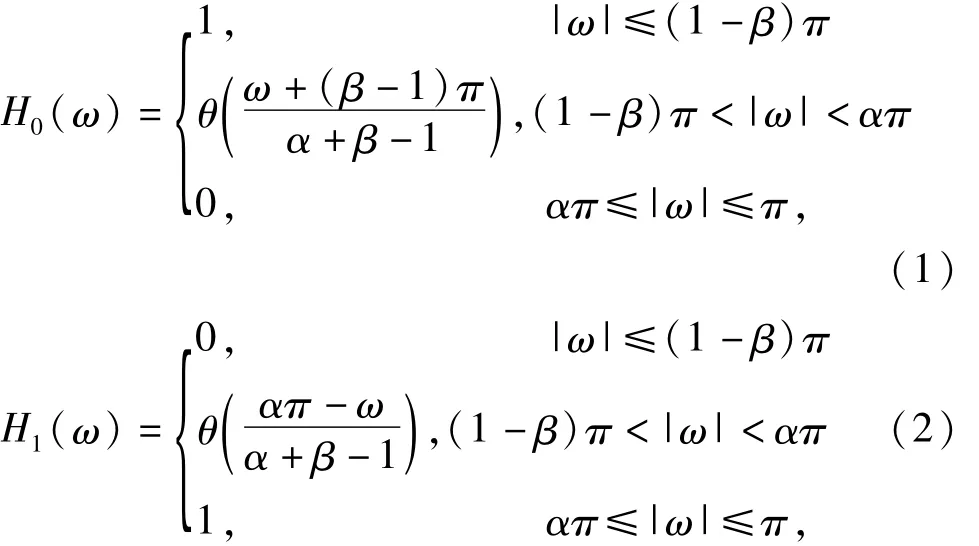
其中，函数θ（ω）表达式如下：

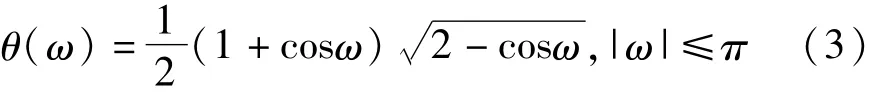
数 θ（ω）源于具有2阶消失矩的Daubechies规范正交基，用于构造低通滤波器H0（ω）和高通滤波器H1（ω）的过渡带，并满足完美的重构条件｜H0（ω）｜2＋｜H1（ω）｜2＝1。

TQWT概念简单、操作灵活，其主要有三个控制参数：品质因子Q，冗余度r和分解层数J。品质因子Q反映了小波基的振荡特性，其值的设定需要满足Q≥1。对于高的Q值，小波具有更多的振荡次数，即包含了更多的振荡周期。这些特性使高Q值TQWT适合分析振荡信号。对于低Q值的TQWT，小波基则具有较少的振荡次数，包含了较少的振荡周期，更适合提取信号中的瞬态冲击成分。在频率分辨率上，TQWT遵循小波变换的分解思想，即对低频尺度不断细化分割而保留高频尺度不变。冗余度r为TQWT小波系数长度与待分析信号长度的比值。冗余度r的值必须严格大于1。为了能够使得小波具有较好的时域局部化能力，推荐r≥3。在本研究中，设置r＝3。

两组不同参数的TQWT小波函数及其频率响应见图2。通过观察，可以总结得到TQWT的一些重要性质。当品质因子Q增大时，小波函数的振荡特性增强。同时，品质因子Q还决定了TQWT带通滤波器的宽度。由图2可知，对于Q＝1（Q值较低）的TQWT，其带通滤波器较宽，此时只需较少的分解层数即可覆盖待分析信号的频谱。反之，对于Q＝4（Q值较高）的TQWT，其带通滤波器较窄，此时则需要较多的分解层数才能覆盖信号的整个频谱。同时，TQWT能够通过基2快速傅里叶变换实现，计算效率高。

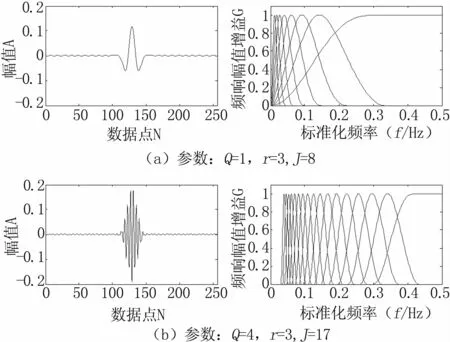
图2 两组不同控制参数的TQWT小波函数及其频率响应图Fig 2 TQWT wavelets and frequency responses for two sets different parameters

2.2 支持向量机（SVM）

支持向量机（SVM）是一种基于统计学习理论的通用机器学习算法，是由Vapnik等于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出特有的优势，已经成为机器学习界的研究热点之一［8］。SVM是一种二类分类模型，构造SVM的过程就是通过解一个凸二次规划问题，找到能分开两类训练数据的最优超平面过程.此处，最优分类超平面，是指此分类面不仅能正确地分开两类样本集，且能使这两类间的间隔最大，其基本思想可以用图3来说明。平面上有两种不同颜色的形状分别代表两类样本，在本研究癫痫EEG信号的分类应用中，一种对应为健康人在清醒状态下的EEG样本，另一种则为癫痫患者在发作时的EEG样本，直线H表示最优分类超平面，H1和H2分别表示各类样本中距离最优超平面最近的样本点且与最优超平面平行的直线，它们之间的距离称为分类间隔。位于H1和H2上距离超平面最近的样本点被称为“支持向量”。与传统的人工神经网络相比，SVM不仅结构简单，而且泛化能力明显提高［9］。

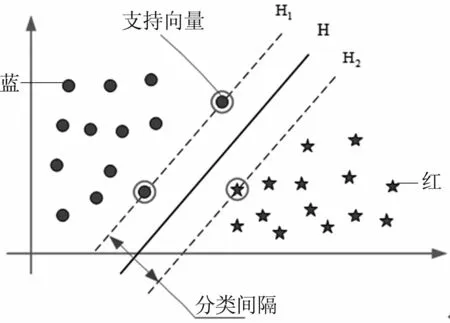
图3 SVM最优分类面示意图Fig 3 Illustration of the SVM optimal classification

在实际分类应用中，对于给定训练样本集D＝｛（x1，y1），（x2，y2），…，（xm，ym）｝，yi∈｛-1，＋1｝，SVM的核心内容为建构出最好的分类超平面。在样本空间中，超平面的划分可通过公式（4）来描述：

其中ω为法向量，b为位移项。样本空间中任意点x到超平面（ω，b）的距离可表示为：

为了找到具有最大分类间隔的划分超平面，SVM分类器可以归纳为求解如下所示的约束优化问题［9］：

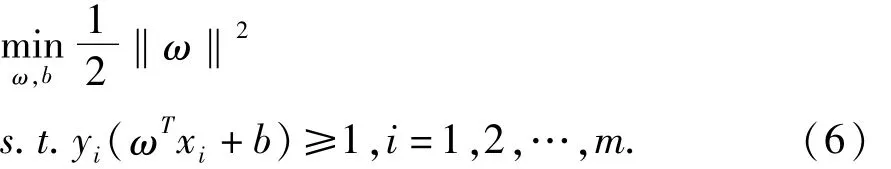
因此，SVM是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即SVM的学习策略是间隔最大化，最终可转化为一个凸二次规划问题的求解。

3 基于TQWT的癫痫EEG信号自动识别方法

本研究提出了基于TQWT的癫痫EEG信号自适应分析与识别方法，其具体的分析流程见图4。该方法在特征提取一步中采用特征提取效果更好的TQWT，而在分类识别中选用SVM分类器，这样构成的新方法可以充分发挥TQWT的特征提取能力与SVM的分类效果。此外，由于癫痫发作时采集得到的EEG信号中会有异常特征波，且信号的波动较为剧烈，幅度高于未发作时EEG信号的波幅［1］。因此，我们提取TQWT处理过的重构EEG信号中的有效值和峰峰值指标用于构成特征分量。有效值和峰峰值指标计算公式分别如下：

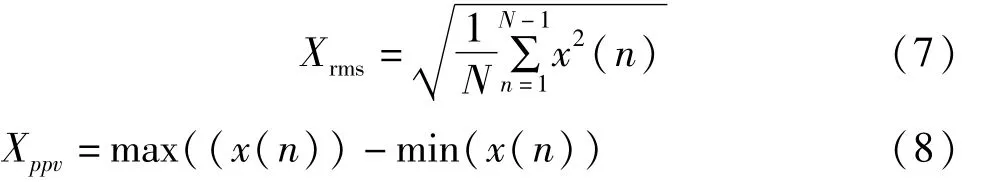
基于TQWT的癫痫EEG信号自适应分析与识别方法可归纳为以下四个步骤：

（1）对原始采样EEG信号进行J层TQWT小波分解，得到J＋1层TQWT小波系数；

（2）根据癫痫异常波对应的频率范围自适应的选择相应TQWT小波子波带进行重构；

（3）对重构EEG信号提取有效值和峰峰值构成特征分量；

（4）采用SVM进行癫痫EEG信号的分类识别。

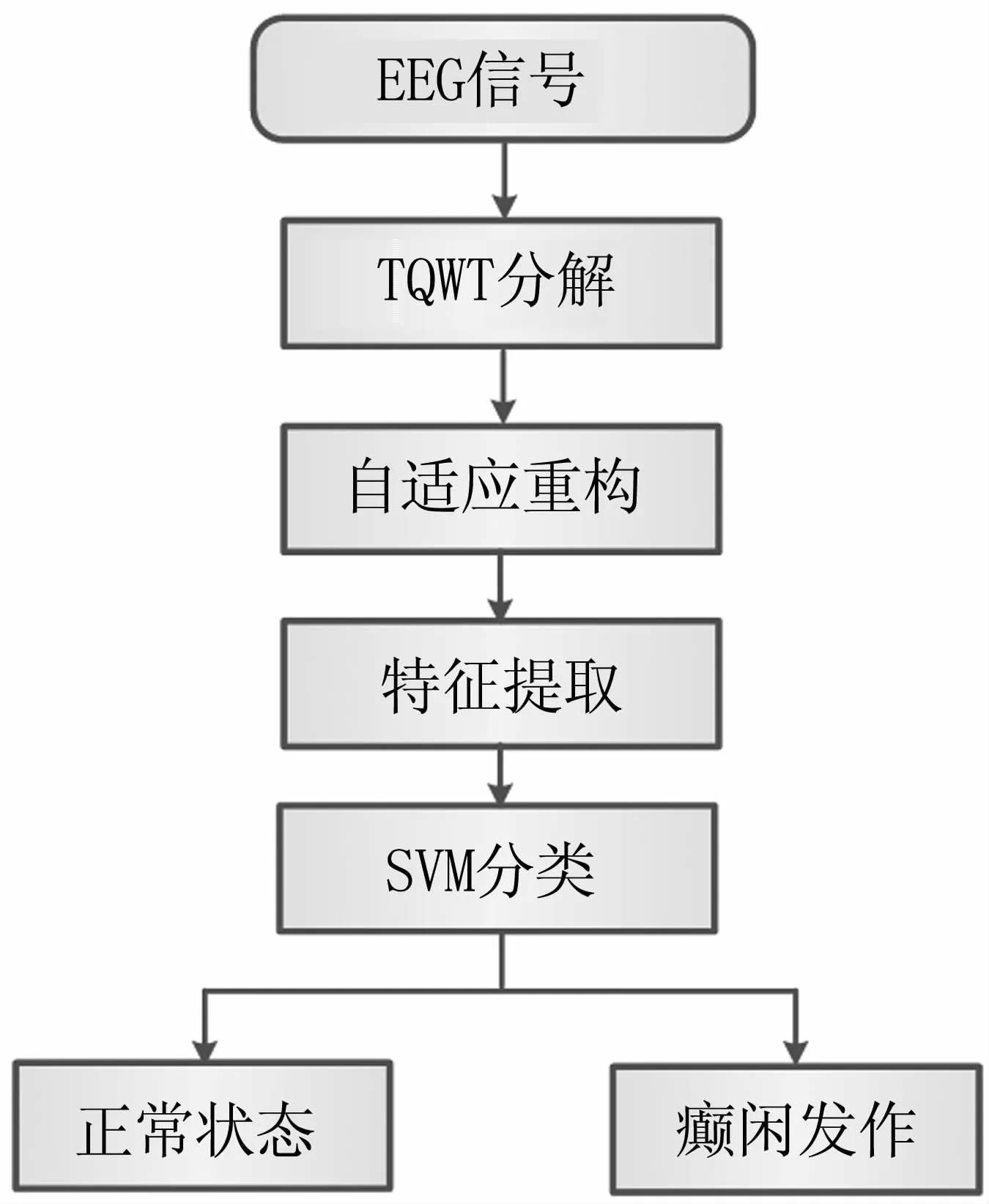
图4 基于TQWT的癫痫EEG信号自适应分析与识别流程Fig 4 Procedure of the proposed method for of identifying and classifying epileptic EEG signals based on the TQWT

4 实验验证及结果分析

本研究将所提出方法应用于癫痫EEG信号的自动识别中，以德国伯恩大学癫痫研究中心采集的典型脑电数据进行验证（数据下载网址：http：//epileptologie-bonn.de/cms/front＿content.php？idcat＝193）。该EEG数据库中的每个样本长度为23.6 s，采样频率为173.6 Hz，每种状态下采集的数据样本数为100。本研究从该癫痫数据库中选取健康人在清醒状态下眼睛张开时以及癫痫患者在发作时的EEG数据进行分析，其中每种测试状态下各选取100组数据样本，利用50组EEG数据进行训练，剩余EEG信号用于测试所提出方法的准确性。

图5为采用TQWT对正常状态下的EEG信号的分解结果。图6为采用 TQWT对癫痫发作时EEG信号的分解结果，可以观察到反应癫痫发作时的棘波、尖波和棘-慢复合波等特征波形被分解到各个小波子波带中。将本研究所提出的基于TQWT的癫痫EEG信号自适应分析与识别方法用于分析该典型数据库中的EEG信号。首先，在对原始采样EEG信号进行TQWT小波分解时，TQWT的参数设置为Q＝1.5，r＝3，J＝6。TQWT分解第 j层对应的中心频率fc可由下式计算得到［6］：

式中：fs为采样频率，α和β分别为低通和高通尺度参数，这两个参数与TQWT的品质因子Q和冗余度r之间的关系如下式所示：

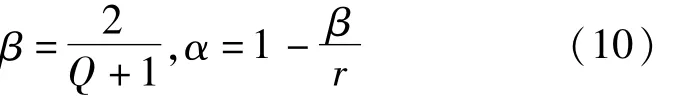
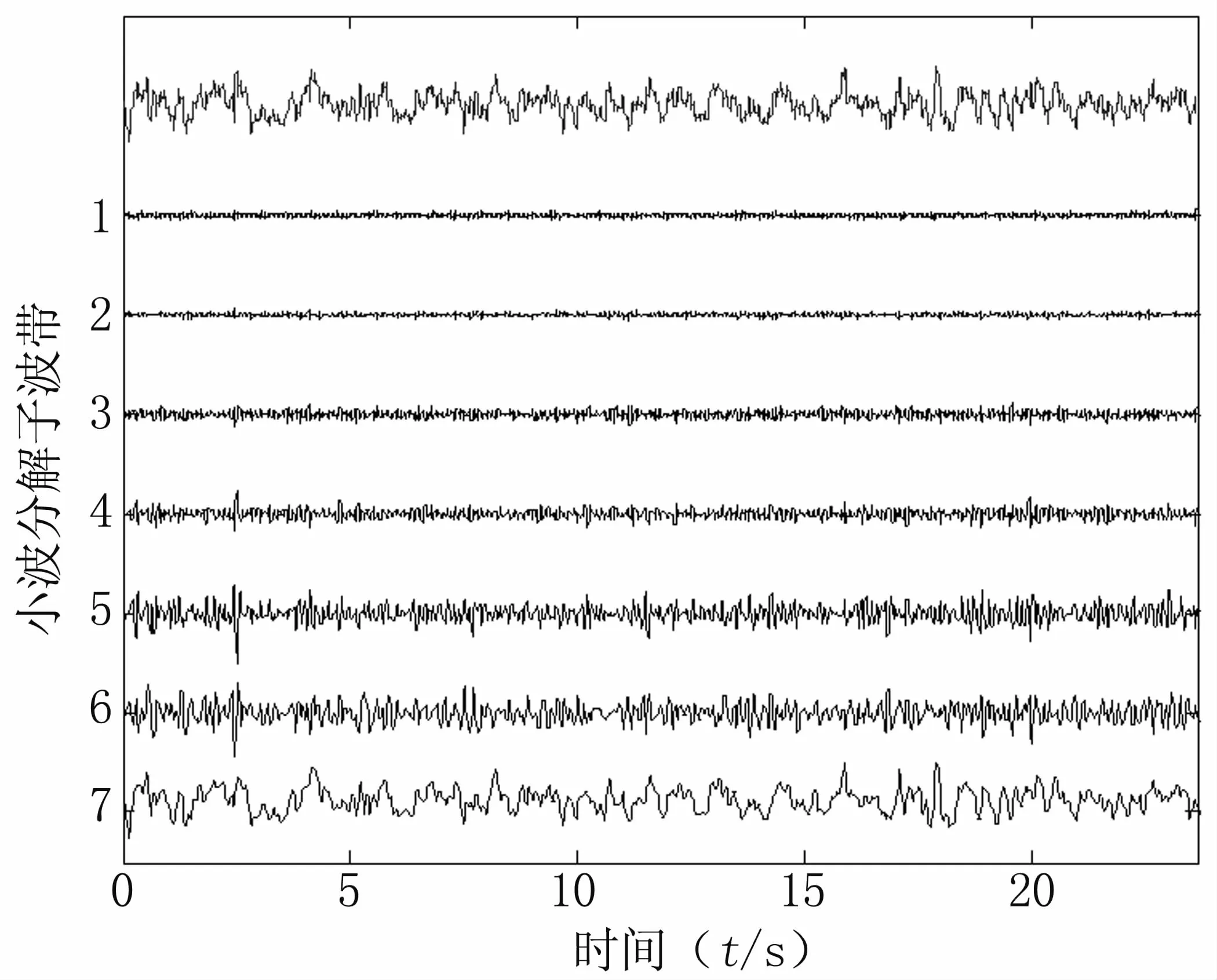
图5 采用TQWT对正常状态下EEG信号的分解结果Fig 5 TQWT decomposed results of EEG signal under healthy status

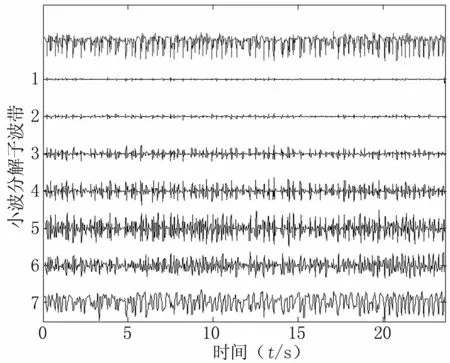
图6 采用TQWT对癫痫发作时EEG信号的分解结果Fig 6 TQWT decomposed results of epileptic abnormal EEG signal

因此，根据TQWT所选择的相应参数值及癫痫EEG信号采样频率173.6 Hz可以计算得到每层小波子波带对应的中心频率分别为：86.81、38.19、28、20.54、15.06和11.05 Hz。由于癫痫EEG异常波对应的频率范围大致在3～25 Hz［4］，这一频率范围大致包含在TQWT分解后的3～6小波子波带中，所以选择3至6层TQWT小波子波带自适应地对EEG信号进行重构。对重构信号提取有效值和峰峰值指标构成特征分量。然后采用SVM进行癫痫EEG信号的分类识别。实验测试结果为：所提出的自适应识别方法对正常和癫痫发作期EEG信号的分类准确率可达98%。

5 结论

本研究针对癫痫EEG信号的识别难题，提出了一种基于TQWT的癫痫EEG信号自适应分析与识别方法，该方法可以有效地实现癫痫EEG信号的自动检测与识别。

引入灵活的TQWT对EEG信号进行分解，进而根据癫痫异常波对应的频率范围自适应的选择相应小波子波带进行重构，并提取有效值和峰峰值指标构成特征分量。最后，采用SVM进行癫痫EEG信号的分类识别。

将本研究所提出的癫痫EEG信号自适应分析与识别方法以德国伯恩大学癫痫研究中心采集的EEG数据为验证对象，分析了健康人在清醒状态下眼睛睁开时以及癫痫患者在发作时的EEG实际数据，对正常和癫痫发作期EEG信号的分类准确率可达98%，验证了方法的有效性。

本研究采用TQWT对EEG信号进行分解，可以实现与EEG特征波形的灵活匹配。然而，TQWT的控制参数仍然需要人为的进行设置，因此，在实际应用中依然依赖专业技术人员和诊断专家。针对具体的待分析EEG信号，如何实现TQWT的自动分解是后续研究的主要工作。