fMRI血液动力学响应模型的参数敏感性分析及优化*
杨增宇,蒋文涛,陈宇
(四川大学工程力学系,成都610065)
1 引 言
近年来,功能磁共振成像(fMRI)已经成为研究大脑动作方式的首要选择方法[1-3]。其原理主要是,BOLD-FMRI图像以体素为单位把神经元活动引起的生理活动记录下来,针对每个体素,我们观测得到的FMRI数据相当于一个时间序列,如果将神经元的活动引起的生理活动的变化统称为神经活动的血液动力学响应,那么可以采用如下的方式来描述:观测到的体素时间序列=血液动力学响应+漂移+噪声[4]。因此,要探究fMRI数据与神经活动的关系,研究血液动力学响应是关键。如果用X(t)表示血流动力学响应,u(t)表示神经活动,h(t)表示相应的血液动力学响应函数,那么在线性时不变系统模型[5-6]中 X(t),u(t),h(t)之间的关系可以表示为:X(t)=u(t)×h(t),即血流动力学响应等于神经活动与血液动力学响应函数的卷积。因此一旦对血液动力学响应函数有了相当的认识就可以预测由某种神经活动模式所导致的血流动力学响应进而得到体素时间序列,实现fMRI成像功能。
2 标准血液动力学响应模型
由于血液动力学响应函数直接影响观测的体素时间序列,所以对于血液动力学响应函数的研究具有重要意义。目前三参数gamma函数形式是fMRI数据处理的研究中应用最为广泛的血液动力学响应函数之一。1994年Friston等[7]提出可以用gamma函数的形式来表征血液动力学响应函数,在此基础上Cohen[8]于1996年提出了三参数形式的血液动力学响应函数模型:

众多研究[9]已经表明上述标准的血液动力学响应函数模型在描述和预测血液动力学响应时具有一定的合理性和有效性,然而由于在实验数据拟合时未考虑参数间的耦合作用,导致得到的函数模型在求解精度和拟合效果上都并非最优,迄今国内外针对血液动力学响应函数的研究几乎没有对该三参数模型进行相应的优化处理工作。本研究将以此模型为基本框架,通过拟合实验数据值对其进行优化。
3 参数敏感性分析
由3参数控制的血液动力学响应模型,由于各参数对最终信号响应值的影响程度是不同的:影响大的参数即使有微小摄动,都会引起流动应力的较大波动,甚至吞没了其他相对不敏感参数的作用。因此,有必要对由实验数据确定的血液动力学响应模型的参数进行敏感度分析。
3.1 参数敏感度分析方法
拉丁超立方抽样(LHS)是一种均匀空间抽样方法,最早于1979年由simpson等提出,具有抽样次数较少、可有效避免重复抽样等特点,适用于对复杂的多维参数空间抽样[10]。抽样过程如下:
(1)设变量X的取值范围为[a,b],所需抽取的样本个数为n。
(2)将X的取值范围[a,b]等概率的分为 n个区间,并在每个区间中随机的抽取一个数作为Xi的一个样本值,将所取的值进行随机排列,由此可得到关于Xi的样本容量为n的样本序列:{x1,x2,x3……xn}。
(3)对于m维参数空间(即含有m个变量)的抽样,则是对 m个变量(X1,X2,X3……Xm)均进行步骤1和步骤2,得到m个样本序列。
(4)对m个样本序列各取一个值即可获得一个m维的样本参数集,共可得到n个m维的样本参数集,见表1,此即完成了拉丁超立方抽样的全过程。

表1 多参数LHS抽样样本参数集Table 1 Sample parameter set of Multi parameter LHS sampling
Spearman秩相关系数是一个非参数性质(与分布无关)的秩统计参数[11],由 Spearman在1904年提出,用于度量两个随机变量之间的相关方向与密切程度,在统计学中,Spearman秩相关系数一般由希腊字母ρs表示。设变量X的样本集为{x1,x2,x3……xn},将其按照从大到小的顺序进行排列,得到一个有序序列{x1′,x2′,x3′……xn′}。定义原始 xi在新的有序序列{x1′,x2′,x3′……xn′}中所占的位置Ki为 xi在样本集{x1,x2,x3……xn}中的秩。设与 X对应的变量Y的样本参数集为{y1,y2,y3……yn}。设 xk在{x1,x2,x3……xn}中的秩为 αk,yk在{y1,y2,y3……yn}中的秩为 βk,则相应的 spearman秩相关系数的计算公式为:
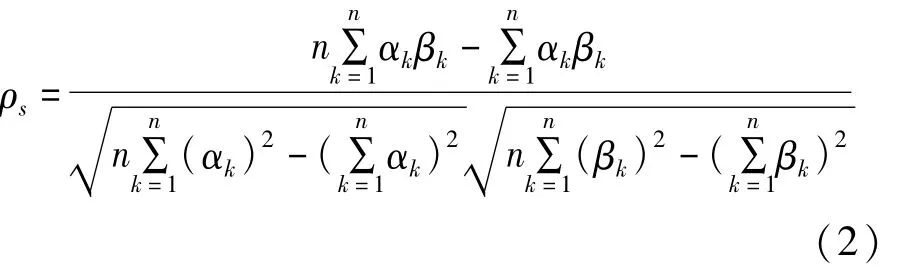
Spearman秩相关系数即反映了该参数的敏感度[8]。
3.2 参数敏感度分析结果
对模型参数(k、n、m)进行超立方抽样,形成 p个3维的样本参数集,见表2,每个参数集对应一个具体血液动力学响应函数模型。
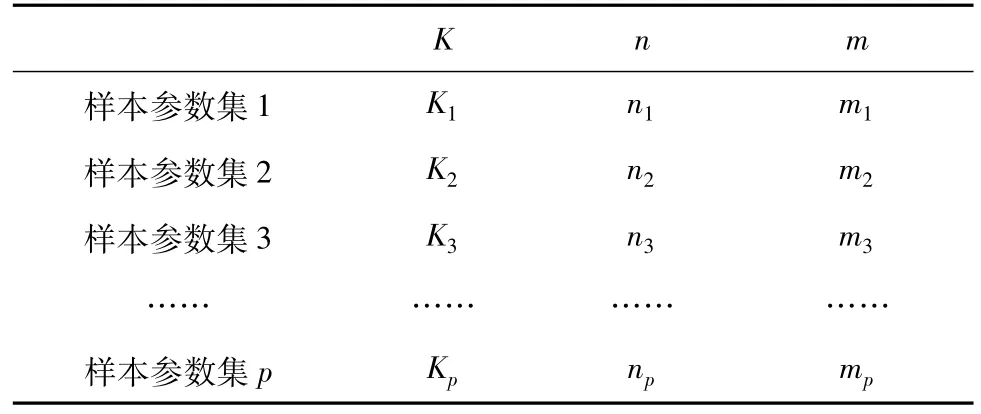
表2 血液动力学响应模型的LHS抽样样本参数集Table 2 LHS sampling parameter set of hemodynamic response model
将所得到的各个样本参数集的参数带入模型中,依据文献[8]中实验的时间节点值计算出相应的信号强度h*,而文献[8]中实验测得的信号强度为h,根据最小二乘拟合的原理,计算目标函数值W,依据spearman秩的定义和式(1),利用所得的 W值分别和相应的 k、n、m值计算spearman秩相关系数,从而得到参数敏感度,见表3。

表3 模型参数敏感度统计表Table 3 Statistics of model parameter sensitivity
由表3中数据可知:(1)当各参数的取值范围一定时,响应函数的参数敏感性估计受抽样次数的影响,并且抽样次数越大,各参数的敏感度越趋于稳定。所以为了取得较真实、较准确的模型参数敏感度,应将抽样次数取得足够大,以保证所得到的敏感性分析结果有效性及合理性。当抽样次数由500次增加至1 000次时参数敏感度波动很小,故可认为500次抽样结果已经足够稳定,能够代表样本特征,此时的数据具有分析和应用价值。(2)当保持参数k、m取值范围以及抽样次数一定(均为500次),只改变参数n的取值范围时,各参数敏感度均存在较大的波动,故各参数敏感度不仅与其自身的取值范围有关,还与其他参数的取值范围相关,即模型参数间的耦合作用对分析结果的影响很大。(3)三个参数k、m、n中,m和 n的参数敏感度相当,而 k的参数敏感度较小,与m、n相比有很大差异。即m、n对目标函数的影响较大,为了使各个参数都有相当的参数敏感度,应该使各个参数对目标函数的spearman秩相关系数都接近0.333,然而这样又会将k值的取值区间设置得过小,不利于后续的优化搜索工作,故我们取表中k、m、n参数敏感度最接近的情况,即取初始取值区间为:k:[0,10]m:[0,40]n:[-20,20]
4 优化与分析
4.1 模型优化算法—遗传算法
遗传算法是一种模仿生物的遗传进化原理,通过选择、交叉与变异等操作机制,使种群中个体的适应性不断提高,从而找到问题的满意解或最优解的仿生全局优化算法[12]。
遗传算法基本流程框见图1。在参数的初始取值区间范围内随机取值,作为一个个体,将所有初始个体组成的群体称为初始种群,对初始种群中每个个体进行二进制编码,所得到的二进制字符串通常称为该个体的“染色体”;设置合理的适应度函数,计算初始种群的适应度值,并进行是否终止进化的判断;对于种群需要多次进化才能满足求解要求的问题,对上一代种群进行选择(轮盘赌方法选择新一代进化种群)、交叉(两两个体之间按照交叉概率交换他们的部分染色体片段)、变异(每个个体按照变异概率改变某一个或某些基因座上的基因值为其它的等位基因)等运算得到新一代种群,并判断是否满足终止进化条件。
4.2 模型优化分析
根据参数敏感性分析结果,对模型中的3个参数给定初始取值区间:k:[0,10],m:[0,40],n:[-20,20],利用matlab平台编写遗传算法程序,以文献[8]中实验值为基础,分别取遗传代数为50、100、500、1 000对模型参数进行最优值求解,最终,求得使目标函数W(x)最小时所对应的参数即响应模型:

图1 遗传算法基本流程框图Fig 1 Basic flow diagram of genetic algorithm
50代:[k,m,n]=[21.654,1.878,-0.891]h(t)=21.654t1.878e-0.891t
100代:[k,m,n]=[17.017,7.393,-2.358]h(t)=17.017t7.393e-2.358t
500代:[k,m,n]=[2.095,6.699,-1.538]h(t)=2.095t6.699e-1.538t
1000代:[k,m,n]=[0.518,7.780,-1.601]h(t)=0.518t7.780e-1.601t
2000代:[k,m,n]=[0.457,8.460,-1.804]h(t)=0.457t8.460e-1.804t
将所得模型与文献[8]中实验值进行拟合效果比较:

图2 不同遗传代数拟合效果比较Fig 2 Comparison of fitting effect inthe different genetic algebra
由图2可知随着遗传代数的增加,通过优化搜索所得的模型的拟合效果越来越好;算法显示出较快的收敛性,当遗传代数为100代时所得模型已经初步具有实验值曲线的轮廓;当遗传代数多于1 000代时,代与代之间差距较小,已经接近最优的模型曲线。
4.3 模型优化结果
取遗传代数为2500代(可以认为此时目标函数已收敛到最小值),进行遗传算法最优搜索,得到优化的模型为:
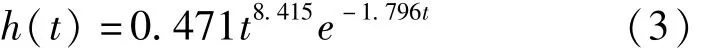
而根据文献[8]中实验值,由Cohen利用最小二乘法确定的三参数形式的血液动力学响应函数模型为:
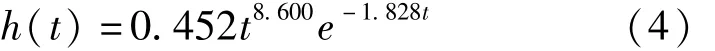
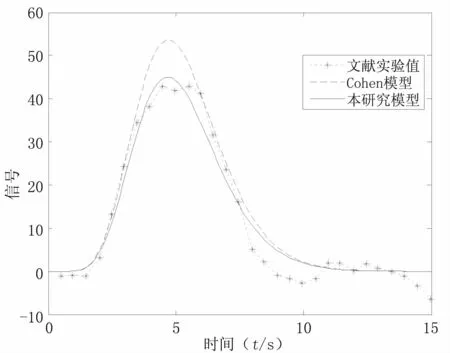
图3 Cohen模型与本研究模型的比较Fig 3 Comparison of the Cohen model with the model presented in this study
由图3可知Cohen模型与本研究所建立的模型都能够描述相应的血流动力学响应,但是本研究所建立的模型能够更加贴合实验曲线,具有更高的求解精度与更好的拟合效果。
5 经典算例分析
为了说明优化的响应模型能够较好的描述与预测由神经活动(u)所引起的血液动力学响应(X),本研究以一个OFF-ON任务为例,任务数据取自文献[13]Savoy及其学生做的视觉闪光实验,实验采用方波刺激,有交替的45 s的刺激和休息时间,实验记录下fMRI信号随时间的变化过程。利用Cohen模型以及所得到的优化后的响应模型式(4)来进行比较与验证,可以得到图4的血液动力学响应,图中灰色区域表示刺激期,白色区域表示休息期,连续曲线为神经活动(此处为δ(t)阶跃函数)和响应函数的卷积的形成的响应预测曲线。可以看到,(1)响应信号相对任务的开始时间有一定的延迟,在任务结束后也需要一定的时间回到基线水平,这与通常观测到的fMRI信号特点是吻合的。(2)与传统的Cohen模型相比较,本研究所得优化模型能够更好描述和预测由神经活动所引起的血液动力学响应,所得结果更加接近真实值。
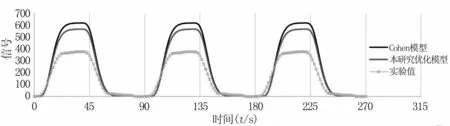
图4 OFF-ON任务响应图Fig 4 OFF-ON task response diagram
6 结论
血液动力学响应函数模型参数的敏感度受其他参数的取值范围的影响,故不能单独研究某一材料参数的敏感度,表明本研究的LHS和spearman秩相关结合的整体分析方法对于该问题是适合的。本研究采用参数敏感度估计搜索区域和遗传算法结合的方法能够很好的实现血液动力学响应函数模型的参数识别。所用于最优化处理的遗传算法具有较好的收敛性与普适性。建立的优化模型能够很好的描述和预测由神经活动引起的血流动力学响应,所得到的预测曲线与通常观测到的fMRI数据特点吻合。此外,本研究建立的优化模型在求解精度和拟合效果上较传统的Cohen模型有一定的提高。

