知其然还要知其所以然

王飞

前段时间我上了一次三角形的内角和的教研课。在试教过程中，我发现很多学生已经知道三角形的内角和是180度这一结论，并且对这一结论深信不疑。在用量一量的方法验证的过程中，别的学生在汇报测量数据时，其他学生就会插嘴，报出最后一个角的度数，问他没有测量怎么知道别人测量的度数呢？他答道：“我是算出来的，因为三角形的内角和是180度。”还有的学生只是为了迎合结论，在测量的过程中会反复调整数据，将测量的结果凑成180度，导致课堂上的探究活动流于形式，达不到应有的教学目的。学生的表现让我反思：如果学生已经知道这个结论，我们的教学该如何设计，才能激发学生的学习兴趣，从而引导他们由质疑走向真探究，切实发展思维呢？

我和数学组的同事一起讨论，形成了如下的教学对策：准确把握学生的学习起点，通过数学家的探索精神激发学生的学习兴趣，引导学生进行一次科学的验证之旅，让学生的思维经历由直观到抽象、由浅入深的过程，更好地满足学生“数学家”的科学探索愿望，感受数学的魅力。

教学片段

师：你们知道三角形的内角和是多少度吗？

生（齐答）：180度。

师：你们都认为是180度，（所有学生点头）现在大家都知道了这个结论，是不是这节课我们就不用上了，老师直接给点题目让你们做就可以？（大部分学生点头，有学生提出测量可能会有误差，不准确）是的，老师怀疑这个结论，那我们这节课还要干点什么？

生：那就要想办法验证这个结论，说服老师。

师：这个孩子具有数学家的天赋。对于这样一个结论，有的同学愿意相信结论再做些习题，有的同学有数学家的天赋，为什么呢？因为他还想知道来历，用科学的方法验证三角形的内角和到底是不是180度，设法让老师相信这个结论。今天让我们当回一数学家，大家有没有兴趣？

学生纷纷点头，然后开始想点子、找办法验证这个结论，整节课就这样进入到验证结论的重心上来。

学生讨论后，分享自己的想法，得到以下几种思路：量一量、折拼、剪拼等。教师将学生分成几个学习小组，各选一种思路进行活动，提出活动建议：（1）选择合适的材料；（2）做好操作的准备：将要操作的三角形的内角标注好序号；（3）在测量过程中一定要实事求是，不要调整数据；（4）做好汇报准备。

量一量的方法。生1汇报：记录好组内4位同学测量后得到的数据，分别是179毅、181毅、180毅、180毅，得出结论：三角形的内角和接近180度。教师表扬学生具备数学家实事求是的品质，强调这个结论对我们研究三角形的内角和非常有价值。

剪拼的方法。生2上台进行剪拼操作：先将3个内角标注好，再剪下来，拿出直尺，将3个内角沿直尺边进行拼接，最后3个内角拼在一起与直尺边重合。学生自信地说：“通过这样的操作，我们得到的结论是三角形的内角和是180度。”

折拼的方法。生3通过找三角形边的中点，将三角形的3个内角折在一起，近似地拼成一个平角。

生4：我这儿有一种不同的方法：用正方形沿对角线对折，两个部分完全重合，而且是两个完全一样的等腰直角三角形。一个等腰直角三角形的内角和是正方形内角和的一半，正方形的内角和是90毅×4=360毅，所以一个等腰直角三角形内角和是正方形内角和的一半，也就是180度。

师：这位孩子的发现真了不起，能够从不同的方面找到解决问题的方法，尽管在逻辑上还存在不足，但是看起来也有道理，通过我们的观察和直觉能够说明等腰直角三角形的内角和是180度。那我们怎么知道一般直角三角形的内角和呢？现在你们有办法了吗？

学生纷纷点头，拿出学具袋中的学具进行探索。很多学生拿到长方形在思考，寻找验证方法。

生5：一般直角三角形可以通过长方形得到，沿长方形对角线剪开就变成了两个直角三角形，我发现对应的角能够完全重合，是两个完全一样的直角三角形。长方形的内角和是360度，沿对角线剪开后，长方形就被平均分成了两半，所以一个直角三角形的内角和就是180度。（教师用课件辅助说明这一验证过程，如图所示）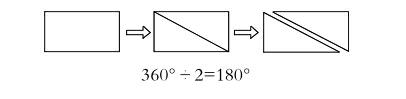

师：在验证直角三角形的内角和是180度的基础上，你能用它来验证其他三角形的内角和是180度吗？

生6：老师，任何一个锐角三角形都可以沿高剪开，分为两个直角三角形。两个直角三角形的和是180度+180度=360度，而其中有两个直角拼在一起成了一条直线，可以看作是一个平角，所以原来锐角三角形的3个内角的和就是360度-180度=180度。（同样的道理可以说明钝角三角形内角和也是180度）

师：你们能化未知为已知，用不同的方法验证三角形的内角和是180度，真会想办法。尽管有些方法还有不足，但你们的大胆思考、勇于表达是数学家最可贵的品质，我们进入中学以后，还会有更加严谨科学的方法来验证它，大家敬请期待吧！

课后反思：三角形的内角和是多少？大部分学生已经知道这一知识点，所以回答起来很容易，但是只知其然而不知其所以然，因此本节课的重点是引导学生知其所以然，用科学的方法验证三角形的内角和是180度，经历一个“相信—质疑—确信”的探究过程。课堂上，学生的操作方法并不单一、测量也不是在凑数据，而是自然而然地出现了操作验证环节中的误差。这一切源于给学生提供了探究的机会，让学生在独立思考和探究的基础上，真正当了一回数学家，独立完成知识的建构。学生的方法是多种多样的，学生的思考也是多方位的。学生从已有的知识经验出发，采用量、剪、拼、折的方法进行验证，这些都是符合学生现阶段认知水平的。在测量和剪拼过程中会有误差，学生难以获得“三角形内角和是180度”的精确感知。正是因为误差的存在，有学生想到了用正方形分成两个等腰直角三角形，根据正方形的内角和是360度，推导出等腰直角三角形的内角和是180度。还有学生想到把长方形沿对角线分成两个直角三角形，通过操作直观感知对应的角完全重合，从而得出其中一个直角三角形的内角和是180度的结论，并由此推导出锐角三角形、钝角三角形的内角和。尽管验证过程存在不足，利用长方形、正方形沿对角线剪开，得到的两个三角形完全重合，是学生在操作层面得到的“看起来是这样”的现实，是基于这一现实基础上的验证与说理。严格地说，这是在已经承认三角形的内角和是180度的基础上进行验证的，从逻辑上来讲是错误的。教师深知这一阶段学生思维的特点，没有直接指出学生具体的逻辑错误（实际上，学生也纠缠不清这中间的邏辑关系与前提），而是对学生这种直觉思维、大胆表达予以肯定和保护，有利于学生积累数学活动经验。最后教师指出在中学里将有一种更科学严谨的逻辑推理方法验证三角形的内角和是180度，为数学的科学与严谨指明了方向。

（作者单位：湘潭市教育科学研究院）endprint