厚度振动模态优化设计

赵慧，王艳，顾亦炜，刘佳



厚度振动模态优化设计

赵慧1，王艳2，顾亦炜1，刘佳1

(1. 上海船舶电子设备研究所，上海201108；2. 水声对抗技术重点实验室，上海201108)

实际工作中，压电陶瓷圆片振子的尺寸是有限的，振子在厚度振动基频处与径向振动高阶模有较强的耦合作用。通过理论计算和有限元仿真分析耦合作用的影响。为优化厚度振动模态，提出在压电圆片振子的中心打孔的方法，用孔径大小来调节径向高阶振动频率。实验证明压电圆片振子在中心打孔对优化厚度振动模态有效。

厚度振动；耦合作用；开孔圆片

0 引言

高频水声换能器在多波束测深系统、反蛙人声呐系统、图像声呐系统等水声系统中有着广泛应用[1]。厚度振动模态是高频水声换能器的主要工作模态[2]。在早期的理论分析中，常用一维振动理论来近似处理厚度极化的压电陶瓷圆片振子的振动问题。当振子的厚度与直径比很小时，这种近似是合理的。但在实际工作中，振子的尺寸是有限的，尤其是当振子的厚度与直径比不是很小时，此时振子的厚度振动基频与径向振动高阶模将出现较强的耦合作用，其振动模式复杂，振动模态不纯[3]。

本文通过解有限尺寸压电圆片振子的多模式耦合振动的频率方程，求得振子的径向及厚度振动的谐振频率，分析耦合作用的影响。为优化厚度振动模态，提出在压电圆片振子的中心打孔的方法，用孔径大小来调节径向高阶振动频率，使得厚度振动基频模态变得纯净。实验证明打孔的方法是有效的，可给高频换能器的设计提供一些参考。

1 压电圆片振子多模耦合振动

耦合振动作用下的实际谐振频率跟圆片振子的尺寸密切相关，厚度振动的谐振基频与常用的一维振动理论有较大的差别。

1.1 频率方程

图1为一沿厚度方向极化的压电陶瓷圆片，直径为2，厚度为2，取轴为极化方向。

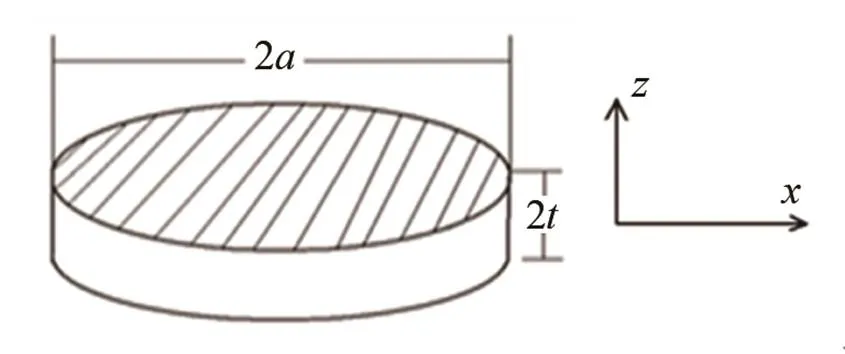
图1 压电圆片振子

根据文献[3]的数值计算结论，分析厚度振动基频和径向振动频率可以忽略压电效应而不会引入大的误差。考虑压电陶瓷的各向异性，得以下力学方程[3]：

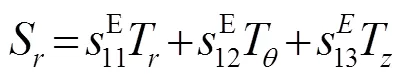
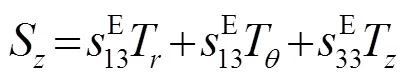
方程(4)、(5)的解为

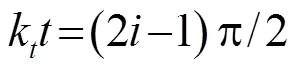
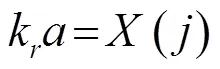
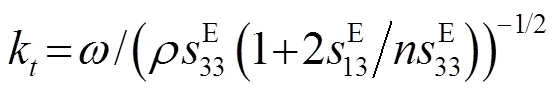
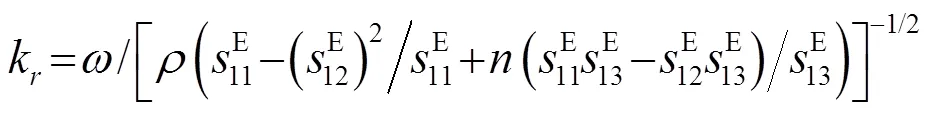
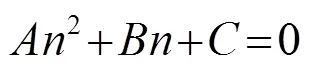
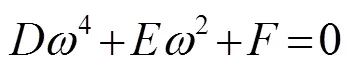
式(10)、(11)中，、、、、、均是常数，其值与圆形陶瓷片的材料以及厚度2和直径2有关。

由此可见，圆形振子的材料和尺寸给定后就可以求得耦合系数及谐振频率，而且振子的谐振频率与振子的厚度和直径尺寸都有关系。这与理想的圆形振子一维振动理论有较大的区别。

1.2 数值计算及结果分析

以直径2=60 mm、厚度2=10 mm的PZT-4压电陶瓷圆片为例计算径向振动和厚度振动的谐振模态。相关的材料参数为

方程(10)中的、、分别为

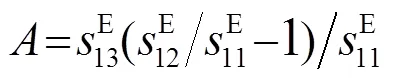
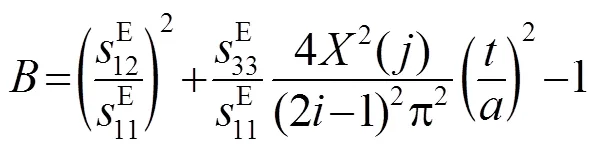
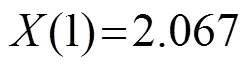
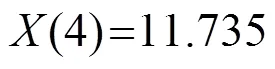
方程(10)中取=1，=1。将材料参数代入、、中，解方程得出耦合系数的值为

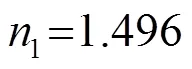
再将耦合系数的值代入到式(8)、(9)中，可以分别得出径向振动和厚度振动的谐振频率值。两个耦合系数的值分别对应着圆形振子的厚度振动和径向振动。表1中的f0、f1、f2、f3分别表示径向振动的基频、一阶、二阶、三阶高次谐波振动频率，0为厚度振动基频。

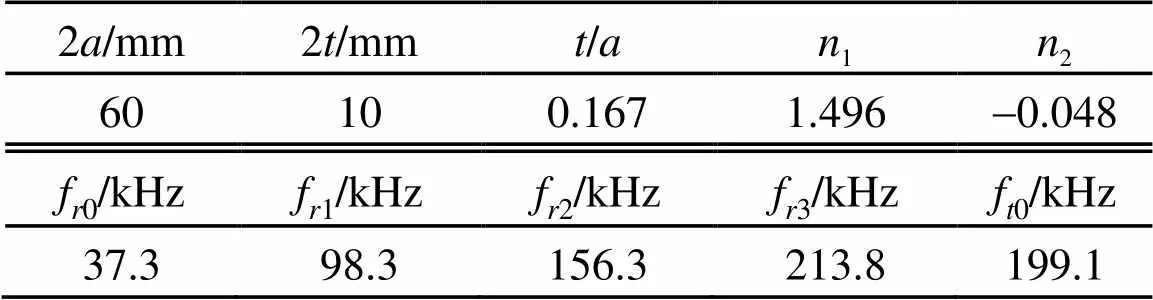
表1 振子厚度振动及径向振动的频率理论计算结果

表1中径向振动的三阶高次谐波振动频率与厚度振动的谐振频率相隔较近，相差只有14.7 kHz。两个耦合系数的数值符号相反，厚度与径向振动之间是反相的，无法耦合到一起。因此厚度振动基频模式会受径向振动的高次谐波振动模式的影响。

1.3 仿真分析耦合振动影响

有限元仿真软件在计算换能器电声性能时会得到很直接明了的结果，但是对于该结果的来源，则需要结合理论计算一起分析。以直径2=60 mm、厚度2=10 mm的PZT-4压电陶瓷圆片为例，计算其厚度振动基频和径向振动的振动模式，结果如表2所示

表2 振子厚度振动及径向振动的频率仿真计算结果

对比表1和表2的计算结果可知，对于径向振动的三阶高次谐波振动频率和厚度振动谐振基频而言，理论模型和有限元仿真结果相差不到1%，吻合较好。说明上文中耦合振动理论计算的方法可行，结果合理。振动模式位移云图如图2、3所示。

图2 200.1 kHz振动模式位移云图

图3 212.4 kHz振动模式位移云图

因为圆形振子具有轴对称特性，所以只需建立轴对称模型，然后在对称轴上施加轴对称边界条件即可[4]。从图2可知，厚度振动基频不是纯净的厚度振动，受到径向振动的高阶振动模式影响。表面的振动幅度是以圆心为轴对称分布的，靠近圆心处振动幅度大，沿径向振动幅度呈波浪状且逐渐减少。

径向振动高阶频率也不是纯净的高阶径向振动，圆形振子表面的振动幅度也不均匀，呈波浪状且逐渐减少。单从振动模式位移云图上分析很难得出哪个频率是厚度振动的基频，只有和理论计算相结合，才能得出结果。

1.4 调节厚度与直径的尺寸对耦合振动的影响

从上述分析可知，厚度振动基频处存在耦合作用的影响，该影响主要来自于径向的高阶模态。虽然厚度振动的基频跟圆形振子的厚度和直径尺寸均有关系，但是从上文的公式推导中可知，调节厚度尺寸对厚度振动的谐振频率影响更大。

以直径2=50 mm、厚度2=10 mm的PZT-4压电陶瓷圆片为例，并以该圆形晶片的谐振频率为基准，计算调节厚度与直径尺寸的谐振频率变化，结果如表3所示。

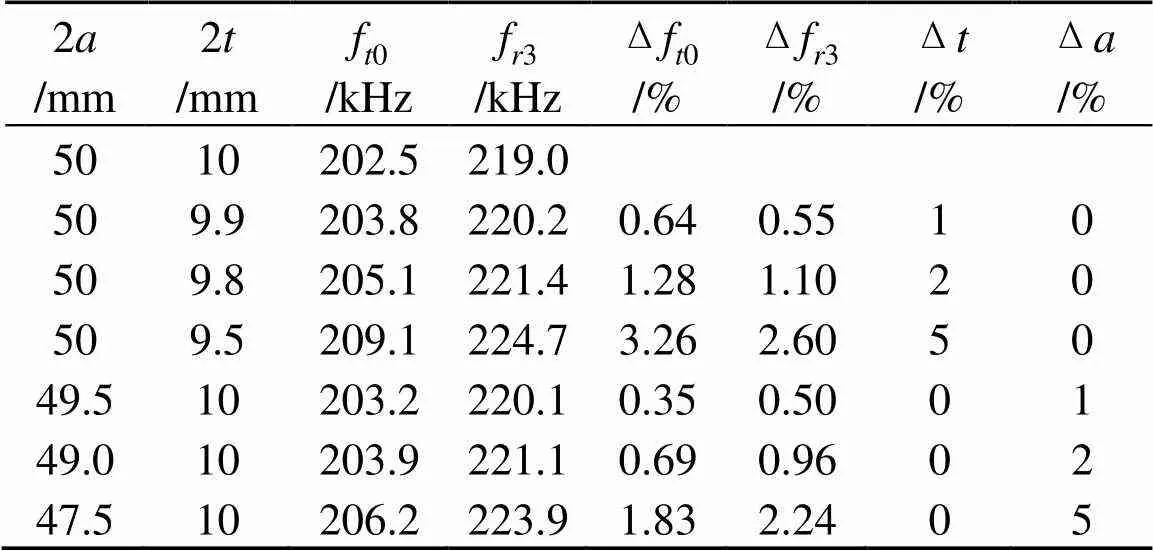
表3 调节厚度与直径尺寸频率变化表

表3计算的结果表明：(1) 直径或者厚度尺寸不变，调节另一个尺寸，厚度谐振基频和径向高阶模频率均会发生变化。(2) 直径不变，调节厚度尺寸，厚度谐振基频的变化率要大于径向高阶模频率变化率；厚度不变，调节直径尺寸，径向高阶模频率变化率要大于厚度谐振基频的变化率。

2 中心开孔法优化圆片换能器厚度振动模态

根据表3的计算结果，圆形振子的直径尺寸固定不变，减少厚度尺寸，振子的厚度谐振频率和径向高阶谐振模频率均增加，只是两者的增加速率不一样。因此若要将两个频率分开得较远，需要将尺寸调节比较多才行。这一点有时在工程应用中是做不到的，因为换能器的工作频率和指向性开角往往是固定的。

本文提出在圆形振子的中心打孔的方法，适当调节外径尺寸，以满足指向性指标。该方法可将径向高阶模和厚度振动基频分开。圆形振子的中心打孔后，径向振动的高阶模将发生变化，整个振动模式也发生改变。

为了有对比性，以直径2=50 mm、厚度2=10 mm的PZT-4压电陶瓷圆片为例，并以该圆形晶片的谐振频率为基准，计算中心挖孔的内径大小为2，对谐振频率的影响结果如表4所示。

表4 调节内径尺寸频率变化表

表4的计算结果表明：(1) 圆形振子的外径和厚度尺寸不变，改变内径大小，厚度谐振基频和径向高阶模频率均会发生变化。(2) 只改变内径大小时，径向高阶模频率的变化率比厚度谐振基频的变化率大得多。(3) 与表3的结果对比，对将厚度振动基频和径向高阶模频率分开，内径大小、厚度尺寸、径向尺寸三个因素中，改变内径大小分开得最快，并且径向高阶模频率对此最敏感。

3 实验

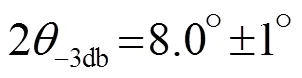
按照厚度振动一维理论和指向性开角公式计算得出，圆形振子的直径尺寸为2=60 mm、厚度尺寸2=10 mm。用该尺寸的压电陶瓷圆形晶片制作的高频活塞换能器的电声性能如图4~6所示。

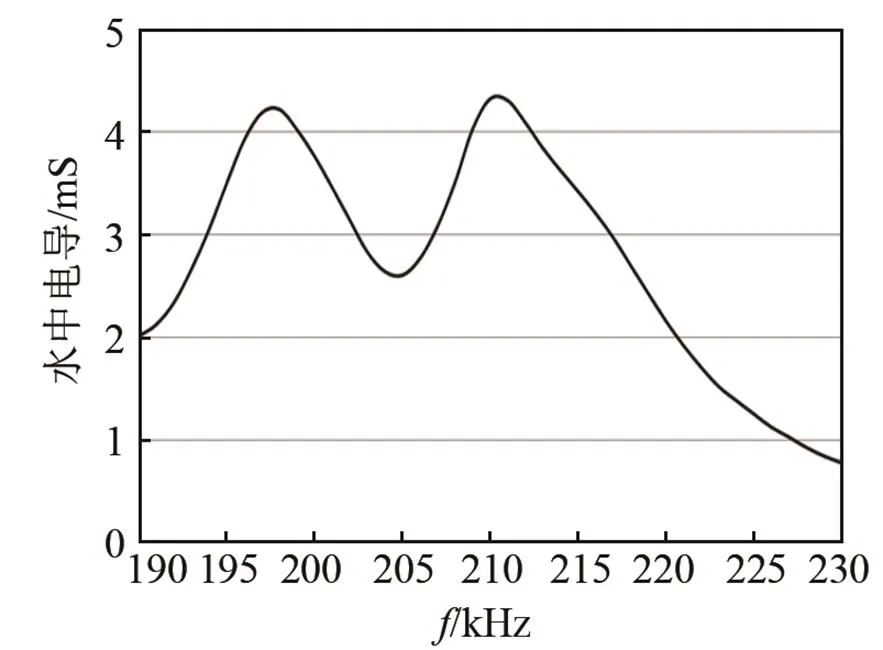
图4 换能器水中电导曲线

图5 换能器发送电压响应级曲线

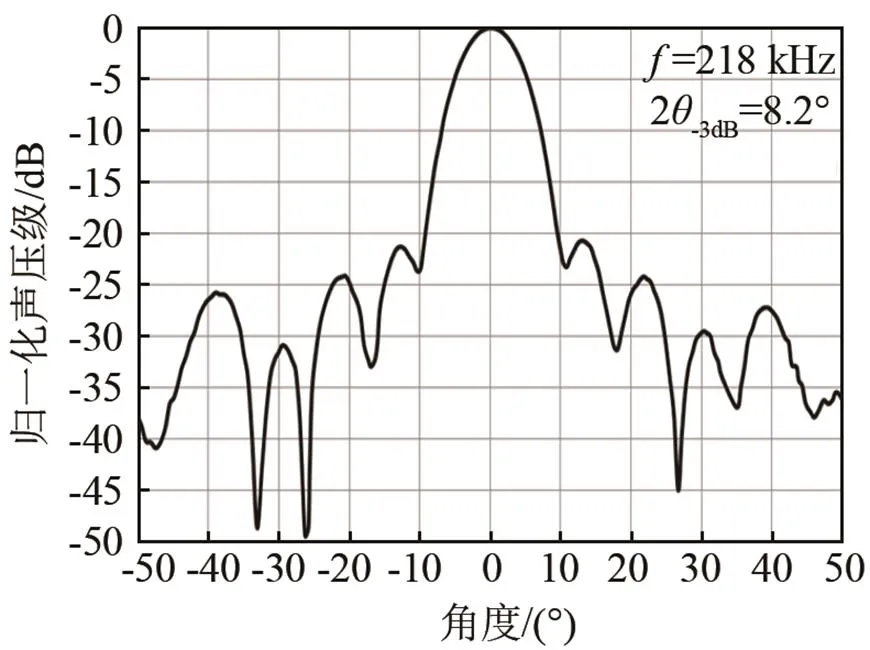
图6 换能器指向性图

为优化厚度振动模态，在圆形振子中心挖孔，设计压电陶瓷晶片尺寸为2=55.8 mm，2=5.1 mm，2=9.1 mm。制作的换能器测试数据如图7~9所示。

两种换能器的测试数据结果对比如表5所示。

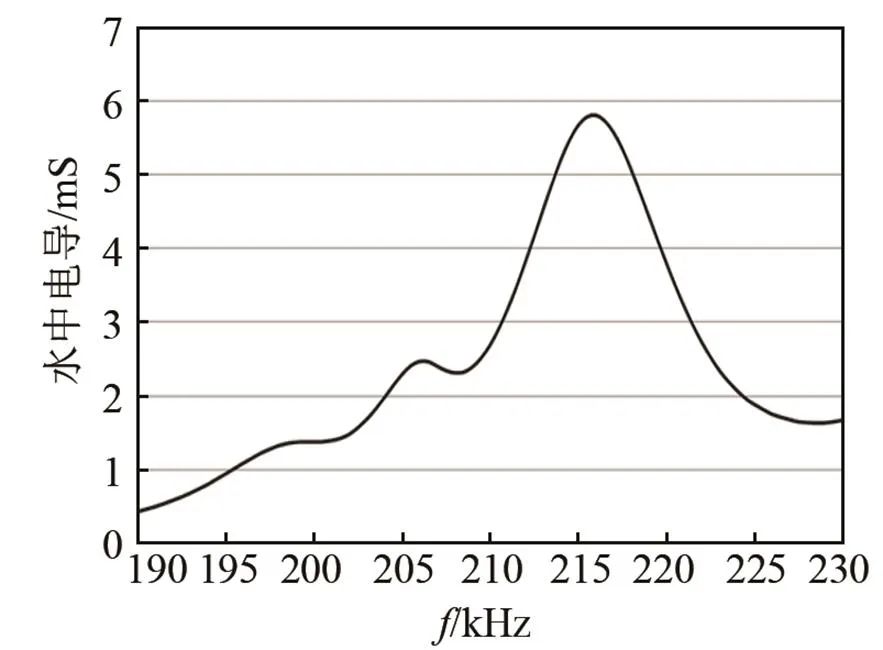
图7 优化设计后换能器水中电导曲线

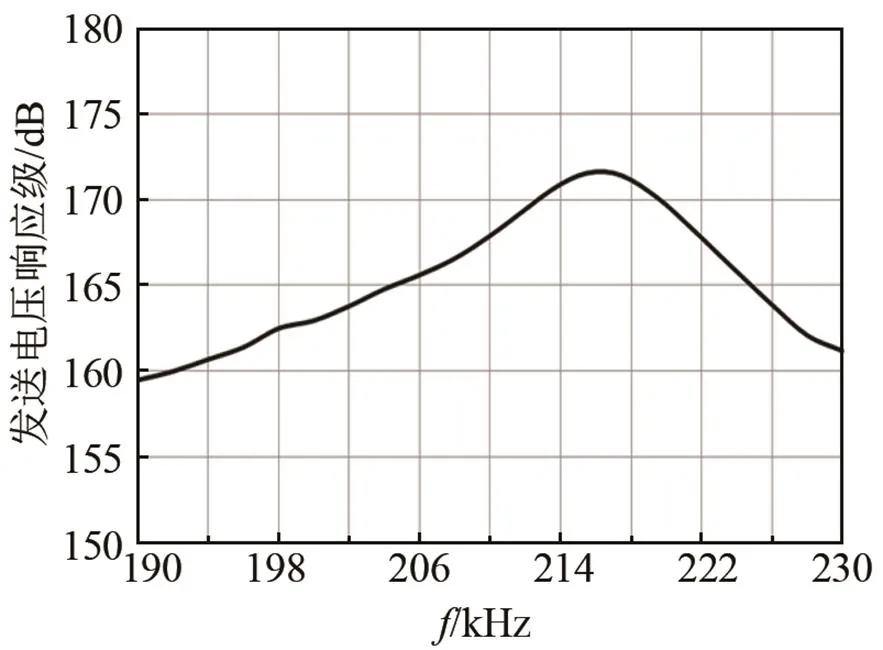
图8 优化设计后换能器发送电压响应级曲线

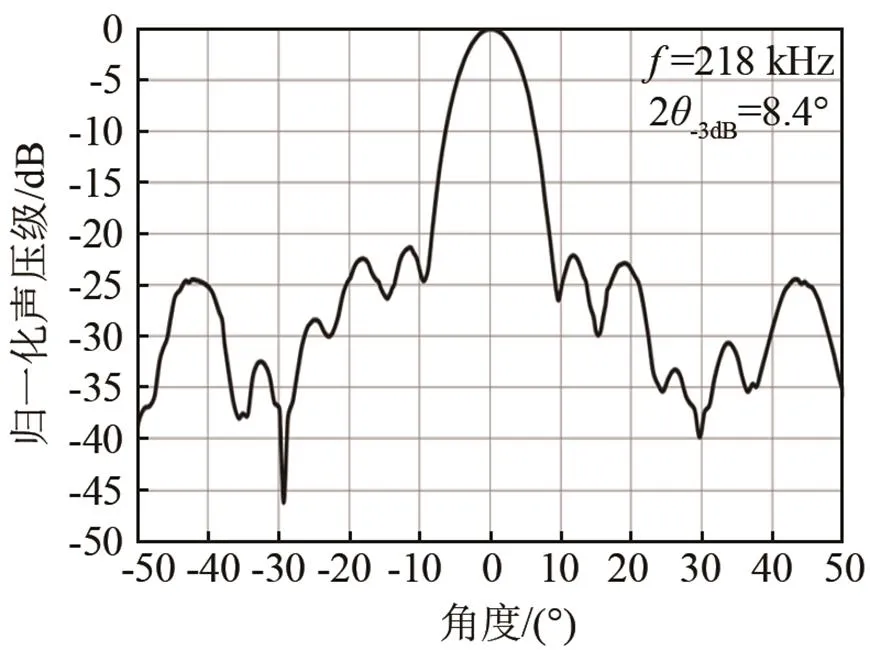
图9 优化设计后换能器指向性图

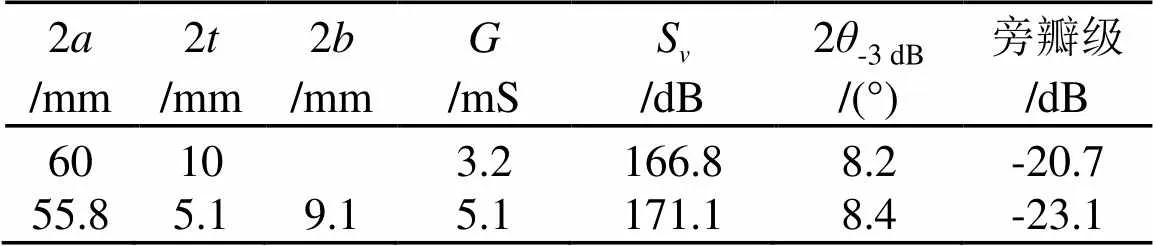
表5 两种规格换能器218 kHz性能对比

对比两种晶片规格的换能器性能可知，通过模态优化，耦合作用的影响明显减少，换能器的发送电压响应得到显著提高，波束宽度和旁瓣级基本保持不变。

4 结论

本文通过理论计算，分析了耦合作用的影响，提出压电陶瓷圆片中心开孔的方法来降低耦合作用的影响。实验证明，中心开孔的振子对优化厚度振动模态有效，为设计高频换能器提供了一个可行的方法。

[1] 吴培荣, 刘振君, 王艳, 等. 一款高频弧形换能器[J]. 声学技术, 2012, 31(6): 628-630. WU Peirong, LIU Zhenjun, WANG Yan, et al. A high frequency underwater transducer curved array[J]. Technical Acoustics, 2012, 31(6): 628-630.

[2] 周利生, 胡青. 水声发射换能器技术研究综述[J]. 哈尔滨工程大学学报, 2010, 31(7): 932-937. ZHOU Lisheng, HU Qing. Summarization of underwater acoustic projector technologies [J]. Journal of Harbin Engineering University, 2010, 31(7): 932-937.

[3] 林书玉, 张福成. 压电陶瓷圆片振子的多模耦合振动[J]. 电子学报, 1994, 12(12): 64-69. LIN Shuyu, ZHANG Fucheng. Multimode coupling vibration in disk plates of piezoelectric ceramics[J]. Acta Electronica Sinica. 1994, 12(12): 64-69.

[4] 莫喜平. 用ANSYS有限元软件模拟分析声学换能器[R]. 中国科学院声学研究所, 2004. MO Xiping. Analyzing the acoustic transducer by ANSYS[R]. In institute of Acoustics, Chinese Academy of Sciences, 2004.

Optimum design of the thickness vibration modal

ZHAO Hui1, WANG Yan2, GU Yi-wei1, LIU Jia1

(1. Shanghai Marine Electronic Equipment Research Institute, Shanghai 201108, China;2. Science and Technology on Underwater Acoustic Antagonizing Laboratory, Shanghai 201108, China)

In actual work, thedimension of PZT piezoelectric ceramics disks is limited.There is a strong coupling between the fundamental frequency of thickness vibration and the higher order modes of radial vibration. In this paper, the impact of coupling is analyzed by theoretical calculation and finite element simulation. In order to optimize the thickness vibration, this paper presents a drilling method at the disk center to adjust the frequency of high order radial vibration by pore size. Experiments show the effectiveness of the drilling method for optimizing the thickness vibration mode.

thickness vibration; coupling effect; holing piezoelectric ceramic disc

TB533

A

1000-3630(2017)-02-0183-05

10.16300/j.cnki.1000-3630.2017.02.015

2016-06-21;

2016-08-20

赵慧(1984－), 男, 湖南衡阳人, 工程师, 研究方向为水声换能器技术。

赵慧, E-mail: zhaohui0094@163.com