基于标准差统计的窄方位角叠前裂缝预测方法

熊晓军 简世凯 李 翔 刘 阳

（油气藏地质及开发工程国家重点实验室（成都理工大学），四川成都610059）

基于标准差统计的窄方位角叠前裂缝预测方法

熊晓军*简世凯 李 翔 刘 阳

（油气藏地质及开发工程国家重点实验室（成都理工大学），四川成都610059）

适用于宽方位角地震数据的常规叠前裂缝检测方法，对大多数窄方位角地震数据难以奏效。为此，本文提出一种基于标准差统计的叠前裂缝预测新方法。该方法的理论基础是地震波在各向异性介质与各向同性介质中传播时会出现一定的AVO差异效应，该差异可细分为两部分：①相同方位角条件下，随入射角变化的AVO曲线间差异；②相同入射角条件下，随方位角变化的AVO曲线间差异。首先利用测井资料和岩石物理模型分析构建研究区背景模型；再对区内窄方位角地震数据进行叠加，得到叠加后的方位角道集数据；然后统计目的层段内各个时间采样点的AVO曲线与背景模型的AVO曲线的差值，并以此差值的标准差表征该时间采样点的裂缝发育强度。渤海M区实际资料的应用效果表明，利用该方法取得的裂缝检测结果与研究区内测井资料解释结果的符合率超过80%。

窄方位角 各向异性 AVO 裂缝预测

1 引言

自20世纪90年代以来，各种裂缝预测技术受到广泛关注。例如：Tsvanskin等［1］研究了HTI介质中动校正速度随方位的变化规律，提出依据纵波在HTI介质中的反射时差预测裂缝参数；Ruger［2］推导了各向异性分界面的反射系数和透射系数随炮检距和方位角变化的公式，为叠前反演奠定了理论基础。近年来，围绕着各向异性介质中AVO梯度、动校正速度、层间旅行时等属性在裂缝预测中的应用日趋火热。Gray［3］基于地震方位角道集数据的AVOZ特征预测裂缝；Bachrach等［4］针对裂缝介质进行了叠前反演，提出通过反演提取裂缝储层参数的方法；Downton等［5］在剖析利用方位角道集预测裂缝的不确定性后，通过改进预测算法提高了裂缝预测的准确性。此外，Feng等［6］根据方位AVO与FVO的交会提高了裂缝检测精度，Perez等［7］利用不同方位速度实现了裂缝预测。因此，利用不同方位角的速度、旅行时、振幅等多种属性都可进行裂缝预测，但这类方法仅适用于宽方位角叠前地震数据。

大多数窄方位角地震数据，尤其是在海洋地震勘探中采集的，对其应用常规的适用于宽方位角的叠前裂缝检测方法，往往不能取得令人满意的效果。截至目前，针对窄方位角地震数据的叠前裂缝检测方法相对较少。田立新等［8］基于远近炮检距属性差异，综合应用叠前弹性参数反演和应力场模拟等技术预测裂缝储层；苏世龙等［9］采取限炮检距接收及一些特殊的数据规则化技术改善窄方位资料特性进而开展叠前裂缝预测。

本文从理论模型的AVO曲线特征分析出发，发现窄方位角采集方式下的各向异性介质模型与各向同性介质模型的AVO曲线具有一定的振幅差异。若能有效地提取该振幅差异，就可用该差异表征裂缝密度发育强度。为此，本文提出了一种适用于窄方位角地震数据的基于标准差统计的叠前裂缝检测新方法，并将其应用于渤海M区的实际资料裂缝检测中，获得了较好的检测效果。

2 理论模型的AVO特征分析

所选研究区位于渤海海域，该区在目的层段普遍发育高角度裂缝。因此，采用HTI介质模型代替实际介质进行窄方位采集的AVO特征分析。

2.1 HTI介质的AVO正演

HTI介质描述的是平行排列的垂直定向裂隙或裂缝模型，它具有水平对称轴，P波在该介质（非裂缝面）中传播时各向异性特征明显。针对该介质模型，Rüger［10］在 Thomsen参数基础上进一步简化，提出了下列纵波反射系数近似计算式

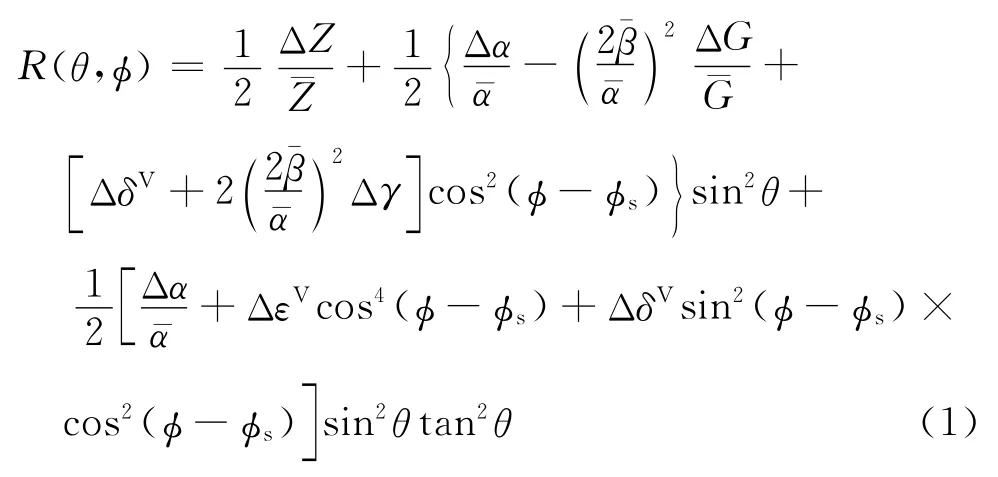
式中：θ为地震波入射角；φ为测线方位角；φs为裂缝走向；为纵波阻抗差与平均纵波阻抗之比；G为横波模量；α为纵波速度；β为横波速度；“Δ”表示界面上、下地层参数之差；上标“V”表示波垂向传播（对应VTI介质）；变量上方的“—”符号表示平均值；ε、δ和γ为Thomsen弱各向异性参数。其中：ε描述纵波速度在垂直与水平方向的差别，表征纵波的各向异性强度；γ描述SH波速度在垂直与水平方向的差别，表征横波的各向异性强度；δ是控制对称轴以外的纵波速度变化，同时也会影响SV波速度，表征纵波的各向异性强度。

在此基础上，当入射角较小（工区内最大炮检距为3701m，目的层最大埋深约为3488m，计算得知其入射角略小于30°）时，式（1）可简化为

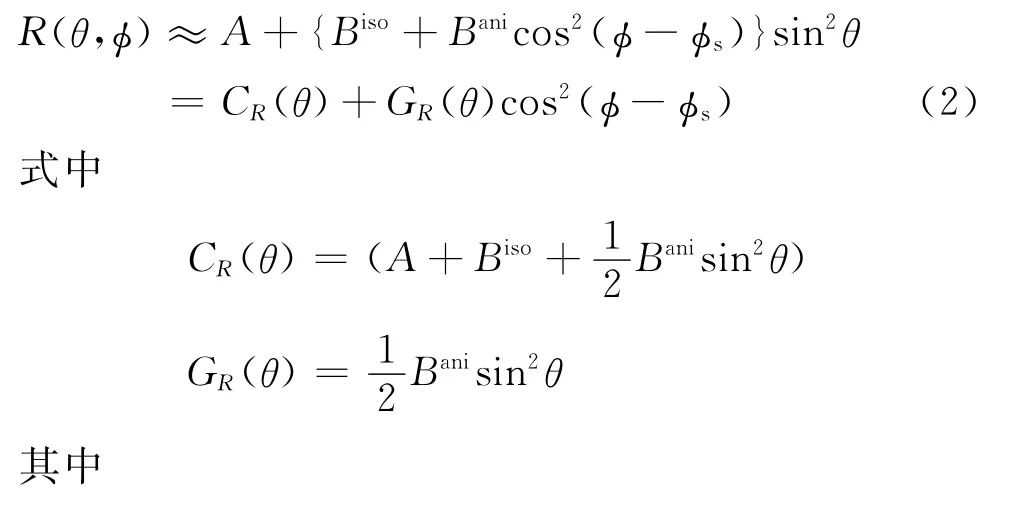
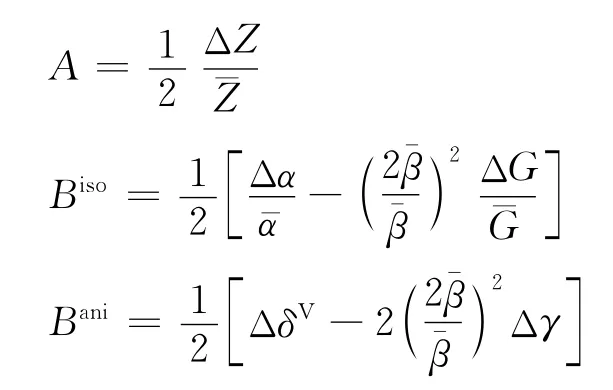
2.2 研究区典型模型AVO模拟

2.2.1 典型裂隙模型的AVO特征模拟

由于AVO模拟是在地层分界面上进行的，而在实际检测过程中，地层内裂缝属性依然有差异，因此笔者在统计区内12口井信息后设计了两类AVO模型：模型1表征由非储层段入射到裂缝储层段情形（表1）；模型2表征由相应的裂缝储层段入射到非储层段情形（表2）。

表1 模型1的参数

表2 模型2的参数

针对上述构建的两类模型及其参数 （表1、表2），在设定方位角为0°时，基于VTI介质模型、常规均匀介质模型及HTI介质模型分别计算纵波在小角度入射时的反射系数，计算结果如图1所示。其中各向异性VTI介质和HTI介质采用Rüger近似式计算，常规均匀介质采用Aki近似式计算。

试算后发现：模型1和模型2在上述三种介质中，反射系数的极性和值域随入射角变化的趋势相反，这与现有理论相符。计算结果显示，HTI介质中的反射系数随入射角的变化最为显著，与VTI介质和常规均匀介质相比，在30°入射角范围内，反射系数极性发生变化的同时其值域也有较大幅度变化。因此，当介质中高陡裂缝发育时，裂缝性质对叠前资料振幅特性的影响不容忽略。

2.2.2 窄方位角HTI介质AVO模拟

地震波在HTI介质中传播，当入射角固定而方位角发生变化时，振幅随方位角变化而呈余弦形态（图2a）。当入射角不同时，纵波反射系数变化也不相同。固定入射角（如设为10°）时，反射系数随方位角的变化较小；当入射角增至40°时，曲线余弦特征明显，变化幅度增大。从图2a可见：当入射角固定时，反射系数随方位角整体变化趋势类似，曲线呈余弦形态。该特征与Rüger［11］的HTI介质模型的实验结果相一致，即在全方位角时也呈现余弦特征，主要与式（1）中的余弦项有关。

图2b说明窄方位叠前地震资料振幅差异虽然较小（黑线表示振幅的平均变化强度），但确实存在。窄方位接收（通常认为有效方位角小于30°）的海上资料，其反射系数随入射角增大而逐渐增大。方位角由0°增至30°时，反射系数随入射角增大的速度有所降低，但反射系数差异明显。

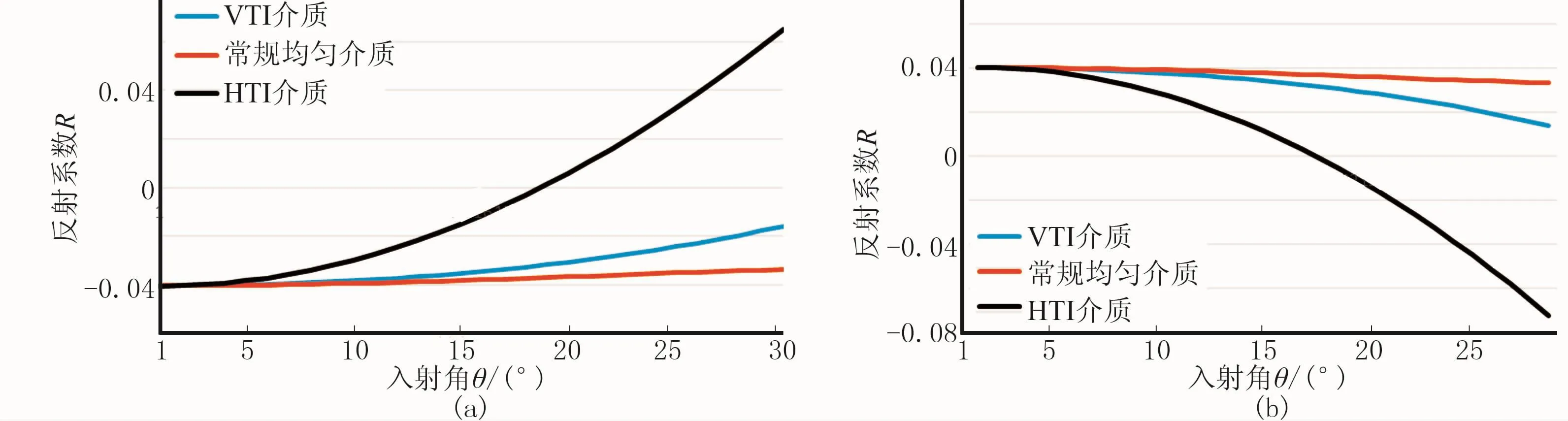
图1 模型1（a）和模型2（b）的 AVO曲线

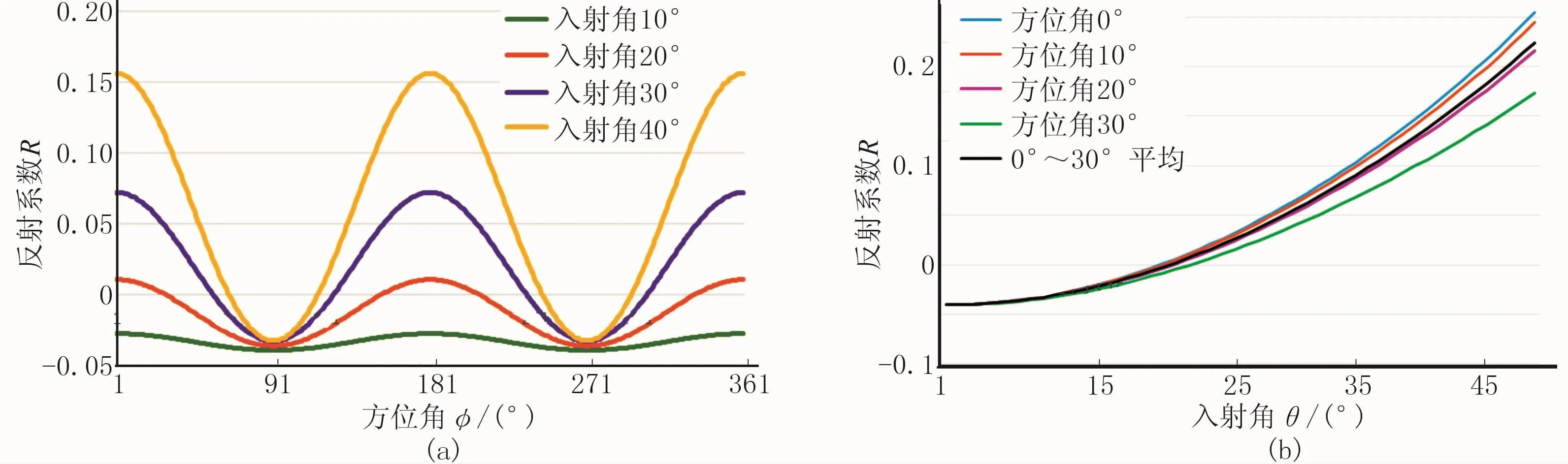
图2 模型1的全方位角（a）和窄方位角（b）的AVO曲线

3 基于标准差统计分析的裂缝检测

上面理论模型的AVO特征分析结果表明，各向异性介质模型与各向同性介质模型具有一定的AVO差异效应，该差异可细分为两部分：①相同方位角条件下，随入射角变化的AVO振幅曲线间差异；②相同入射角条件下，随方位角变化的AVO振幅曲线间差异。基于上述理论分析，本文提出一种针对窄方位角地震数据的叠前裂缝检测新方法。该方法首先基于测井资料和岩石物理模型分析构建研究区背景模型，即各向同性介质模型（不发育裂缝）；接着整理区内窄方位角地震数据，得到多个有效角度道集数据；然后统计目的层段内各个时间采样点的AVO曲线与背景模型的AVO曲线的差值，并以该差值曲线的绝对值之和的标准差表征该时间采样点的裂缝发育强度。包括以下具体计算步骤。

（1）输入叠前地震资料并做预处理。主要包括切除干扰严重的远道集、叠前道集去噪和层拉平处理。

（2）基于三次样条插值对窄方位角资料的振幅特性进行拟合。经此使得实测的振幅曲线在后续计算过程中便于统计，并可在拟合振幅曲线的同时去掉异常值。

（3）基于标准差统计的裂缝密度预测可分为四个步骤。①建立背景振幅曲线：针对常规均匀介质对1类模型和2类模型，据Aki公式分别计算其在30°以内的窄方位角地震AVO特性曲线，统计对应的平均曲线并依据其形态设定为“上升型”（图1a）和“下降型”（图1b）两种典型“样板”曲线。②拟合实测振幅曲线趋势判断：对经样条插值拟合后的实测地震振幅曲线做趋势判断，其中“上升型”曲线反映由非储层向裂缝储层段入射时的AVO特征，“下降型”曲线反映由裂缝储层段向非储层段入射时的AVO特征。③振幅曲线归一化校正：对已做过趋势判断的实测振幅拟合曲线与相应的“样板”曲线做归一化校正，即是将数值较大曲线上各值除以同等倍数，将起点拉至同一位置，使得实测曲线与理论背景曲线在数量级上相同。④振幅异常标准差统计：针对每一个方位角度道集，将某炮检距下拟合后的实测曲线振幅值减去该条件下的背景“样板”曲线在该炮检距下的振幅值，统计其标准差作为该CRP道集处的裂缝密度检测值。统计公式为

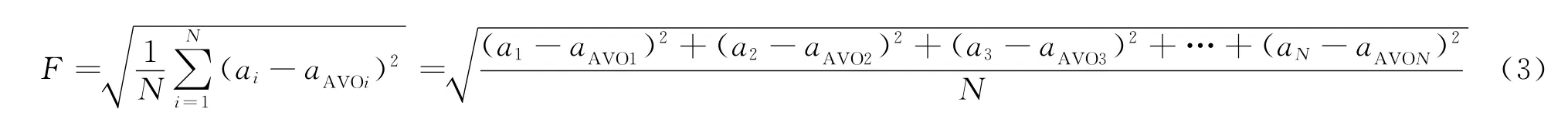
式中：F是振幅差异标准差，可作为裂缝密度参数；ai表示某入射角（炮检距）i下经拟合的实际振幅值；aAVOi表示某入射角（炮检距）i下常规均匀（不含裂缝）介质的AVO特征振幅值（趋势背景值）。

实现过程如图3所示。其中：图3a和图3b是拟合实测振幅曲线在经趋势判断后做同起点校正的示意图，蓝色箭头指示归一化校正方向；图3c和图3d分别是经归一化校正后的图3a和图3b的振幅曲线示意图，图3c表征标准差较大即对应裂缝较发育，图3d表征标准差较小即对应裂缝欠发育。

（4）循环计算三维地震数据体，输出裂缝检测数据体，通过剖面图和平面图汇总、展示检测结果。

图3 基于标准差统计分析的裂缝预测示意图

4 实际资料处理

采用本文提出的基于标准差统计的新方法对渤海M区的潜山裂缝型储层进行裂缝检测。

4.1 叠前道集预处理

基于前面提出的计算流程，针对共反射点叠前道集中常出现的子波一致性、入射角范围、道集不平、信噪比偏低等问题［12-14］，首先对研究区叠前道集数据做预处理，主要是切除干扰严重的远道集、叠前道集去噪及层拉平处理，其目的是为后续裂缝预测提供高品质资料。

图4和图5是区内分别过A5井和A16井的道集预处理分析图，图中蓝色矩形框表示AVO曲线的显示窗口，框内绿色曲线表示拟合AVO曲线，黄色不连续短竖线表示振幅值取样点，红色方点表示以目的层为中心的时窗内拾取的峰值振幅，红色水平线通过目的层位。

从该两图可见，预处理前后拟合曲线变化趋势更符合目的层的AVO变化特征，且图中目的层位（红色水平线处）叠前道集明显被拉平，噪声干扰严重的远道集被剔除。因此，通过预处理，消除了某些非地质影响因素，为后续裂缝预测提供了高质量道集数据。

4.2 裂缝检测及分析

基于预处理后的叠前道集，采用本文提出的新方法在研究区开展裂缝检测，获得了区内裂缝检测数据体——图6和图7分别是过A5井和A16井的裂缝密度检测结果。

图6a是目的层段（目的层及其下延60ms）裂缝检测剖面，图6b是其叠后剖面与目的层段裂缝检测剖面叠加而形成的叠合剖面。从图中可见，A5井在目的层段钻遇裂缝发育区（红色），与实钻中A5井在目的层段钻遇91.3m裂缝型储层的情形相符。

图4 过A5井预处理前（a）、后（b）的道集分析

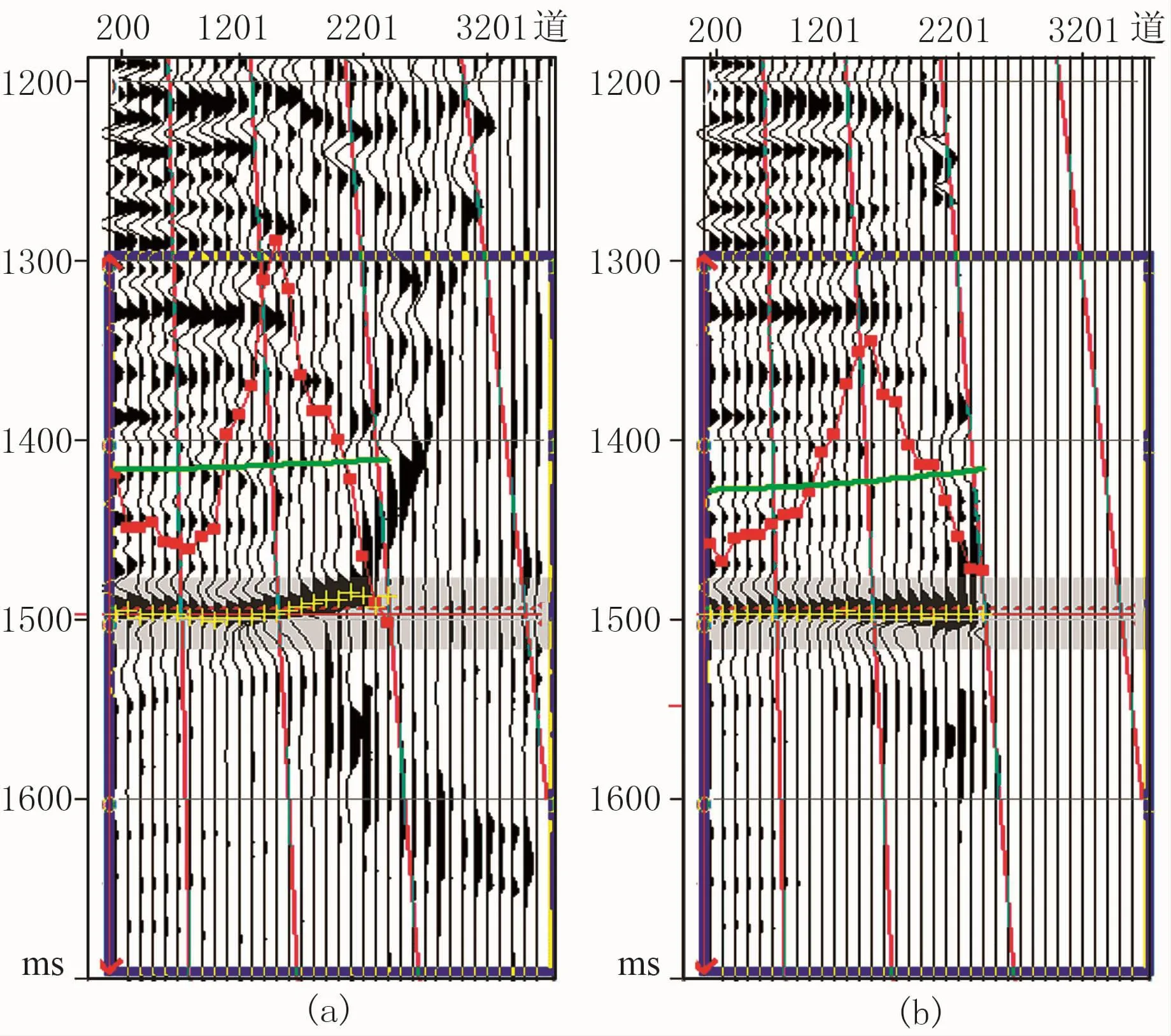
图5 过A16井预处理前（a）、后（b）的道集分析

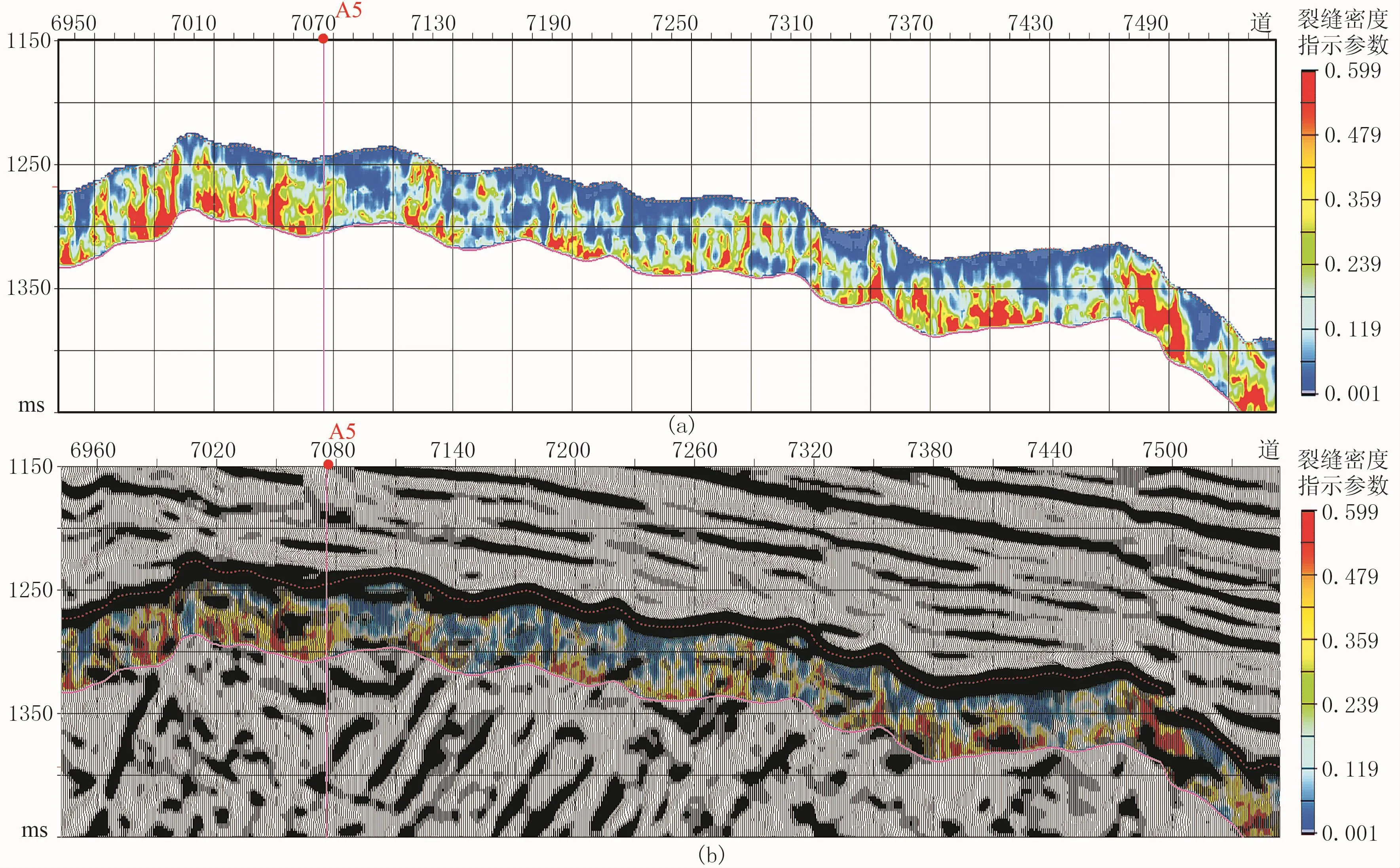
图6 过A5井裂缝检测结果

图7a是目的层段裂缝检测剖面，图7b是其叠合剖面。从该图可见，A16井在目的层段未钻遇裂缝发育区（红色），这与实钻中A16井在目的层段仅钻遇17m裂缝型储层的情形基本相符。

图8是研究区裂缝检测平面图（潜山顶界面至下方60ms范围内的平均值）。从该图可见：工区内共有12口实钻井，其中A3、A6和A12井钻遇变质岩裂缝型储层，且均位于预测平面图的黄色区域（表征裂缝发育）内，故预测结果与实际相符；其余9口井都钻遇花岗岩。在钻遇花岗岩的9口井中：A1、A2、A5、A8、A11、A14和A19等7口井均钻遇裂缝型储层，与预测结果相符的有5口（位于黄色区域）；而A10和A16两井未钻遇裂缝型储层，也与预测结果（位于天蓝色区域）相符合。综上所述，这12口井的预测总符合率为83.3%。

图7 过A16井裂缝检测结果V

图8 研究区三维叠前裂缝检测平面图

5 结论

（1）理论的裂缝模型AVO正演分析结果表明：各向异性介质模型与各向同性介质模型具有一定的AVO差异，该差异可细分为两部分，即方位角恒定时随入射角变化的AVO曲线间差异、入射角不变时随方位角变化的AVO曲线间差异。因此，可利用窄方位角地震数据的AVO特征信息开展裂缝预测。

（2）为了有效地统计分析窄方位角地震资料的AVO振幅特征，对叠前道集数据进行了主要包括切除干扰严重的远道集、叠前道集去噪及层拉平等预处理，这样可为后续的AVO振幅信息的提取与分析提供高信噪比的叠前道集数据。

（3）基于测井资料和岩石物理模型分析引入研究区背景模型，通过均匀介质模型的正演分析，得到窄方位角地震数据的AVO特性曲线，将该曲线幅值作为背景值，与拟合实测振幅曲线进行对比，剔除非裂缝影响因素。

（4）从统计分析窄方位角地震数据AVO特征的角度，提出一种基于标准差统计的窄方位角叠前裂缝检测新方法，即先构建研究区背景模型；再将区内窄方位角地震数据叠加为方位角道集数据；然后统计目的层段内各时间采样点的AVO曲线值与背景模型的AVO曲线值的差，并以该差值的标准差表征该时间采样点的裂缝密度参数。渤海M区实际资料的计算结果验证了该方法的可靠性，其预测符合率超过80%。

［1］ Tsvankin L，Thomsen L.Inversion of reflection travel time for transverse isotropy.Geophysics，1995，60（4）：1095-1107.

［2］ Rüger A.Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media.Gsw Books，2002.

［3］ Gray D，Todorovic-Marinic D.Fracture Detection using 3D Azimuthal AVO.CSEG Recorder，2004.

［4］ Bachrach R，Sengupta M，Salama A et al.Reconstruction of the layer anisotropic elastic parameter and high resolution fracture characterization from P-wave data：A case study using seismic inversion and Bayesian rock physics parameter estimation.Geophysical Prospecting，2009，57（2）：253-262.

［5］ Downton J，Roure R.Azimuthal simultaneous elastic inversion for fracture detection.SEG Technical Program Expanded Abstracts，2010，29：263-267.

［6］ Feng Shen，Jesus S，Dan B et al.Azimuthal offsetdependent attributes （AVO and FVO）applied to fracture detection.SEG Technical Program Expanded Abstracts，1999，18：776-779.

［7］ Perez G，Marfurt K J，Nissen S.Azimuthal binning for improved fracture delineation.SEG Technical Program Expanded Abstracts，2007，26：931-933.

［8］ 田立新，周东红，明君等.窄方位角地震资料在裂缝储层预测中的应用.成都理工大学学报（自然科学版），2010，37（5）：550-553.Tian Lixin，Zhou Donghong，Ming Jun et al.Application of narrow-azimuth seismic data to fractured reservoir prediction.Journal of Chengdu University of Technology（Natural Science Edition），2010，37（5）：550-553.

［9］ 苏世龙，胡丹，黄志等.窄方位角地震数据预测裂缝储层方法.石油地球物理勘探，2015，50（3）：510-515.Su Shilong，Hu Dan，Huang Zhi et al.Fractured reservoir prediction on narrow azimuth seismic data.OGP，2015，50（3）：510-515.

［10］ Rüger A.Using AVO for fracture detection：Analytic basis and practical solutions.The Leading Edge，1997，16（10）：1429-1434.

［11］ Rüger A.Variation of P-wave reflectivity with offset and azimuth in anisotropic media.Geophysics，1998，63（3）：935-947.

［12］ 张津海，张远银，孙赞东.道集品质对叠前AVO／AVA同时反演的影响.石油地球物理勘探，2012，47（1）：68-73.Zhang Jinhai，Zhang Yuanyin，Sun Zandong.The effects of seismic data conditioning on pre-stack AVO／AVA simultaneous inversion.OGP，2012，47（1）：68-73.

［13］ 周鹏，刘志斌，张益明等.一种动态的道集拉平方法研究及应用.断块油气田，2015，22（1）：58-61.Zhou Peng，Liu Zhibin，Zhang Yiming et al.Research and application of a dynamic gather flatten method.Fault-Block Oil＆ Gas Field，2015，22（1）：58-61.

［14］ 赵洲.地震叠前属性及流体识别因子研究［学位论文］.四川成都：成都理工大学，2011.Zhao Zhou.The study of seismic pre-stack attributes and fluid identification factors［D］.Chengdu University of Technology，Chengdu，Sichuan，2011.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.016

熊晓军，简世凯，李翔，刘阳.基于标准差统计的窄方位角叠前裂缝预测方法.石油地球物理勘探，2017，52（1）：114-120.

1000-7210（2017）01-0114-07

*四川省成都市成都理工大学油气藏地质及开发工程国家重点实验室，610059。Email：xiongxiaojun07＠cdut.cn

本文于2016年5月23日收到，最终修改稿于同年12月16日收到。

本项研究受国家自然科学基金项目“Gassmann方程的关键技术研究及其应用”（41274130）资助。

（本文编辑：朱汉东）

熊晓军 教授，1980年生；2002年本科毕业于西南石油大学勘查技术与工程专业，2004年毕业于西南石油大学获地球探测与信息技术专业硕士学位，2007年获成都理工大学地球探测与信息技术专业博士学位；现在成都理工大学主要从事岩石物理分析及油气地震勘探新方法研究。