流注放电低温等离子体中电子输运系数计算的蒙特卡罗模型∗
孙安邦 李晗蔚 许鹏 张冠军
(西安交通大学,电力设备电气绝缘国家重点实验室,西安 710049)
流注放电低温等离子体中电子输运系数计算的蒙特卡罗模型∗
孙安邦†李晗蔚 许鹏 张冠军
(西安交通大学,电力设备电气绝缘国家重点实验室,西安 710049)
流体或者粒子-流体混合数值仿真是研究流注放电基本物理机制的常用手段,而精确的电子输运系数是保证其仿真正确性的必要前提.鉴于现有电子输运系数求解工具存在一定缺陷,本文开发了采用蒙特卡罗方法求解低温等离子体中电子输运系数的仿真工具,测试表明其准确性和精确度均较高.研究了氮氧气体混合比及大气压下三体碰撞吸附对电子输运系数的影响.氮气中流注放电仿真表明,流体仿真中采用本模型改进后的电子输运系数可显著改善流注通道内部的等离子体参数分布.
流注,低温等离子体,电子输运系数,蒙特卡罗模型
1 引 言
流注放电(streamer discharge)通常呈现为明亮的丝状结构,是大气压下气体放电初始阶段的一种常见现象.由于流注头部强烈的电荷聚集效应,使其可以向局部电场低于击穿电场的区域传播[1].在自然界中,流注在闪电的形成阶段起着重要作用,为其产生和传播提供了预电离通道[2].另外,在高空低气压大气层中,流注通常以瞬态发光现象(terrestrial luminescence events,TLEs)的形式存在,比如精灵闪电(sprite)等[3].流注放电在废气/废水净化、生物医学以及辅助燃烧等方面都有着广阔的应用前景[4].
自20世纪40年代流注放电理论被提出以来,科研工作者对流注放电的物理机制进行了大量的数值仿真工作.基于微观描述的粒子模型和基于宏观描述的流体模型是流注放电的两种主要模拟方法.粒子模型可以较为精确地表述流注放电中的随机行为,但是由于需要跟踪百万甚至千万量级的粒子,对计算机的性能要求较高,耗时较长.因此,以往的流注放电数值模以计算效率较高的流体模型为主.近年来,随着计算机性能的提高和数值计算方法的发展,基于空间位置的三维粒子-流体混合模型也逐步建立起来[5,6],其中,流注内部电荷密度高且电场梯度较小的区域采用流体模型,而其外围以及头部电场和电荷密度梯度较高的区域采用粒子模型进行描述,既保证了流注头部敏感区域仿真的可靠性,又很大程度上降低了采用纯粒子方法的计算消耗,是研究流注放电现象的一种高效的仿真手段.
为了保证流体/混合模型的正确性,电子输运系数的精确获取是其中的一个重要因素,包括电子平均能量,漂移、扩散系数以及电离系数等.电子输运系数的获得主要有以下三种手段:1)实验测量;2)求解Boltzmann方程;3)跟踪粒子运动的蒙特卡罗模拟方法.在已有的研究中,BOLSIG+和MAGBOLTZ是两种比较有代表性的电子输运系数求解工具[7,8],长期以来已被广泛采用.然而,两种工具的缺点也较为明显:BOLSIG+基于求解两项近似(“two-term”approximation)的Boltzmann方程,其主要缺点为计算精度较低,特别是强电场下电子的能量分布函数呈现出强烈各向异性的情况下,误差较大[9];MAGBOLTZ采用蒙特卡罗方法求解电子输运系数,其采用内嵌式的粒子碰撞截面,使得用户很难验证其碰撞截面的可靠程度,并无法求解其未内嵌的气体组分.此外,上述两种工具都只能求解电子输运的通量输运系数( fl ux transport coefficient),而无法求解其体输运系数(bulk transport coefficient).近期,Rabie和Franck[10]开发了一套基于MATLAB平台的蒙特卡罗模型METHES,用于计算低温等离子体中电子的输运系数.与MAGBOLTZ比较,METHES可以读取基于‘LXCAT’数据库的电子碰撞截面[11],且可以同时求解电子的通量和体输运系数.然而,METHES在处理电负性气体三体碰撞时存在一定的问题,其一次只能计算某一特定电场的特点使得数据的获取较为繁琐,且采用商业软件Matlab开发,经作者测试发现,其仅适用于Matlab 2014及更新的版本,使用具有一定的局限性.
鉴于上述原因,本文基于Fortran 95平台独立开发了一套用于计算放电低温等离子体中电子输运系数的蒙特卡罗模型,为流注放电的精确数值仿真提供便利.本文开发的工具可以方便地获取任意气体及混合比、任意电场范围内的电子输运系数和能量分布;此外,模型可以方便地采用不同来源的电子碰撞截面,有利于验证数据的正确性,这也是精确模拟流注放电过程的先决条件.
2 蒙特卡罗粒子模拟方法
2.1 电子运动与碰撞处理
电子的运动遵循牛顿-洛伦兹定律,在不考虑磁场作用下,其运动方程为:

式中,me为电子质量,q为电子电荷,v和x分别为电子的速度和位置矢量,E为电场.
模型采用 ‘Velocity Verlet’格式[12]来描述电子的运动,其计算公式为:


其中,vk和xk分别表示电子运动k个时间步长后的速度和位置,∆t为时间步长,ak=qEk/me表示电子在k∆t时刻电子的加速度大小.
由 于 ‘Velocity Verlet’格 式 比 传 统 的 “蛙 跳(leapfrog)”格式对时间步长的要求较低[12],且可较为方便地处理一个时间步长内粒子的多次碰撞问题,因此在流注放电[13,14]以及分子动力学[15]粒子模拟领域被广泛采用.在本文的模型中,空间电荷对电场的影响较小可以忽略,所以可假设电子的加速度为恒定值a0,(3)式可简化为

电子与中性气体之间的碰撞主要包括弹性碰撞、激发以及电离碰撞,若存在电负性气体,需包含电子与中性气体之间的吸附作用.在∆t时间内,电子与中性气体碰撞概率可表示为
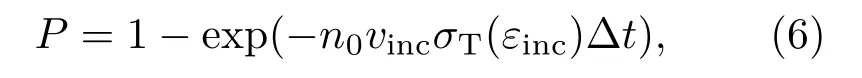
式中,n0表示中性气体数密度,vinc为电子速度,σT(εinc)代表电子与中性气体之间碰撞总截面积,代表电子能量.假设目标粒子总共有N种碰撞,则
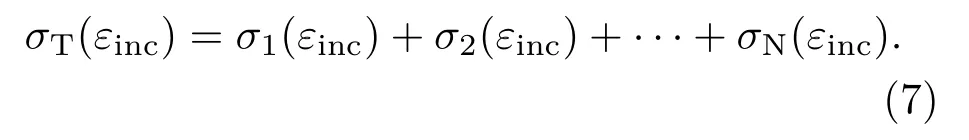
由于在每个时间步长内都要计算所有电子的动能以及碰撞概率,计算量很大.本文采用Birdsall和Vahedi提出的伪碰撞(null collision)方法[16],主要计算步骤如下:
1)计算粒子的最大碰撞频率vc,max,即

2)计算在∆t时间发生碰撞的最大概率,
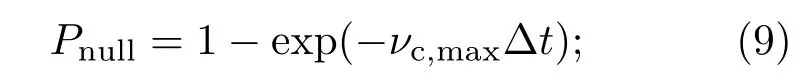
3)计算发生碰撞的最大次数Ncoll,

其中Ntotal为模拟粒子总数;
4)选取介于[0,1]之间的一个随机数RF,若
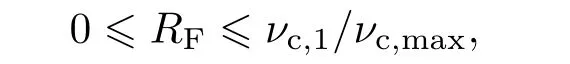
发生第一种碰撞;
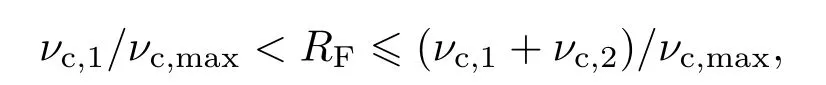
发生第二种碰撞;不做任何处理.

依次循环步骤4),直至发生碰撞的次数达到Ncoll,碰撞循环结束.对于电子发生碰撞后的速度分配,主要采用下述方式处理.
1)若为弹性碰撞,由于电子和中性粒子的质量和速度差异较大,忽略碰撞后电子的能量损失,且碰撞后电子速度服从各向同性分布[17];
2)若为激发碰撞,碰撞后的电子能量为

其中,εex为气体激发阀能,εinc,e和εscat,e分别为碰撞前后电子的动能,且碰撞后的电子速度按照弹性碰撞后相同的方法处理.
3)若为电离碰撞,由能量守恒得到

其中,εscat,e为初始电子碰撞后的能量,εse为电离产生的二次电子能量,εionz为气体电离阀能.对于碰撞后电子的能量分配,一种是采用平均分配的方法,即初始电子和二次电子均分电离后的剩余能量;第二种方法是初始电子碰撞后的能量为

其中,RF为一个介于0到1之间的随机数,B为已知函数(单位:eV).碰撞后的二次电子的能量为

模型对两种不同的能量分配方式进行了测试,其对电子输运系数基本无影响,在本文的计算中均采用第一种即能量平均分配的方法.两个电子的速度均采用与弹性碰撞相同的方法处理.
4)若电子与电负性气体发生吸附作用,则在模型中直接删除该电子的所有信息.
2.2 固定模拟电子数目方法
由于非守恒碰撞(non-conservative collisions)的存在,比如,在电场较高时,电离碰撞引发电子数目呈指数增长,大大减缓了计算收敛的时间,且很容易使得粒子数目超过计算机的能力范围,使得程序中断;相反,在电场较低时,电负性气体的存在使得电子大量吸附在气体分子上,电子数的迅速下降会引起计算误差变大或者出错.图1给出了大气压下纯氧中电子数目在不同约化电场(reduced electric fi eld)下的变化曲线,可以看出,由于电负性氧分子的吸附作用,在电场为20 Td(1 Td=10−21V/m2)时,电子数目从106减少到零的时间约为8 ns,而在1 Td时仅需2 ns.
为了防止计算中电子个数快速增加或者衰减,本文采用以下策略来维持电子数目稳定:首先设定模拟中所期望的电子数目(Ne),若电子数目增长超过(Ne+∆Ne),随机删除∆Ne个电子;若电子数减少至(Ne−∆Ne),则新增加∆Ne个模拟电子,新增电子随机拷贝剩余电子中∆Ne个电子的属性.本文模型可根据需要灵活的设定∆Ne的数值,经测试发现,∆Ne设定为(0.5–1)Ne与不采用固定电子数目模拟相对比,对计算结果的影响基本可以忽略.此外,在本文所采用的电场范围内,电离所引起的电子数目增长基本不会超出计算机的能力范围,因此,此电子数控制策略主要在于解决电负性气体的吸附效应带来的电子数剧减问题,且对输运系数的计算精度影响较小.需要说明的是,以往研究工作者还采用人工电离的方法,即一个电子被吸附则人为添加一个新的电子,以到达类似的控制目的.若模型中取∆Ne=1,则与文献[18]中的处理基本一致.

图1 (网刊彩色)大气压下纯氧中电子数目在不同电场下随时间的变化Fig.1.(color online)Decay of the number of electrons for di ff erent reduced electric fi eld in atmospheric oxygen.
2.3 电子输运系数计算
2.3.1 电子的体输运和通量输运系数
体输运速度表征在外部电场作用下所有电子的质心位置变化,而通量输运速度则表示电子质心位置的变化率[6,18,19].在实际统计中,质心位置不仅仅由电子的漂移决定,非守恒碰撞(电离碰撞或者吸附)所引起的电子能量变化对其影响也较大.相比较而言,体输运系数更易在实验中测得,而通量输运系数在常压下特别是高电场的情况下较难测量.两者的关系可表示为

其中,vb和vf分别表示电子的体以及通量漂移速度,S表示非守恒碰撞效应.很显然,在非守恒碰撞不存在的条件下,vb和vf应具有相同的数值.
在蒙特卡罗模型中,电子的体迁移(µb)和扩散(Db)系数分别表示为:
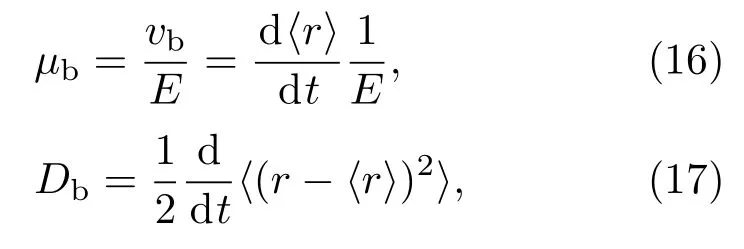
其中,r和〈r〉分别表示电子实时位置和平均位置.
类似地,电子的通量迁移及扩散系数为:

在实际应用中,体输运系数和通量输运系数的适用范围存在差异.如,体输运系数一般可由实验测量直接获得,适用于从实验数据反推粒子的碰撞截面;而通量传输系数则已证明在流注放电以及阻性板室中放电行为的流体以及混合模拟中较为适用[6,18].两种输运系数的异同及其适用范围将在后续的工作中详细探讨,本文中不做赘述.
2.3.2 电离系数
若模型中不采用固定数量的模拟电子个数,电离系数(α)可直接由电子个数的增长率获得,即
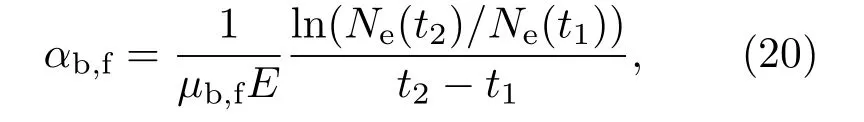
其中,Ne(t2)和Ne(t1)分别表示t2和t1两个时刻的电子总数.
若采用如2.2节介绍的固定模拟电子个数的方法,则通过统计平均电离和吸附频率的方法获得电离系数,可表示为

2.3.3 电子平均能量
电子的平均能量可表示为
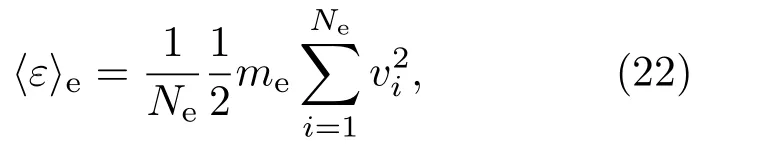
其中,Ne表示电子数目.
2.4 计算流程
本文计算电子输运参数的流程如图2所示.初始时刻设定所需计算的电场范围、气体种类、温度以及混合比等;当前模型可以直接读取来源于‘LXCAT’数据库的电子与任意气体的碰撞截面;电子初始位置设置为0,初始能量假设为0.1 eV且速度服从Maxwell分布.

图2 计算流程图Fig.2.Flow chart of the calculation.
计算过程中,跟踪电子在电场中的运动以更新其速度和位置信息,进而通过蒙特卡罗法处理电子与中性气体之间的弹性以及非弹性碰撞.由于非守恒碰撞的存在,模型设定固定数量的计算粒子以避免电子数的快速增加或者减少.最后,通过模拟足够长的时间(电子的能量分布达到稳态)并比较当前时刻与上一时刻计算参数的差异判断是否达到稳态,若电子输运系数达到稳态,则输出具体信息,否则循环上述步骤.
3 模拟结果与讨论
模拟中所采用的参数如下:气体压强p=105Pa,气体温度T=293 K.模拟开始时采用的电子个数Ne=10000.电场范围取0.1–500 Td.电子的碰撞截面从LXCAT数据库中获得[11].
3.1 模型准确性验证
为了验证模型的准确性,本文与BOLSIG+以及METHES比较了计算得到的氮气及氧气中的通量传输系数.选取氮气和氧气是具有代表性的,分别表征普通和电负性两种不同气体.电子与氮气分子和氧气分子的碰撞截面均来自Biagiv8.9[11].图3给出了电子漂移系数,平均能量,横向、纵向扩散系数以及电离系数随约化电场的变化情况.对比可知,本模型计算得到的电子通量漂移系数(图3(a))、电子平均能量(图3(b))与BOLSIG+及METHES求解所得具有高度的一致性;模型得到的横向以及纵向扩散系数(图3(c)和图3(d))与METHES也较为一致,但是与BOLSIG+有较大差别,特别是在电场大于100 Td后,差别较为突出.这主要是由于BOLSIG+通过求解两项近似的Boltzmann方程获得电子输运系数,其精确度对于分子气体来说较低,且在高电场下电子速度偏离Maxwell分布下其计算误差更大[18].此外,由BOLSOG+得到的电离系数与本模型以及METHES也有细微差别,如图3(e)所示.值得说明的是,在此三类模型中,都忽略或未恰当处理空气中的三体碰撞,其影响将在3.3节中详细讨论.

图3 (网刊彩色)当前模型计算得到的电子通量输运系数与METHES以及BOLSIG+计算结果对比 (a)迁移系数;(b)平均能量;(c),(d)横向及轴向扩散系数;(e)电离系数Fig.3.(color online)Comparison of the electron fl ux transport coefficients between current model,METHES and BOLSIG+:(a)Drift coefficient;(b)mean energy;(c)transverse and longitudinal di ff usion coefficient;(e)ionization rate coefficient.
3.2 氮氧气体混合比对输运系数的影响
不同氮氧混合比气体中流注的放电形态近年来被广泛研究,其中一个重要特征是在含氧量较高的氮氧混合气体中流注呈现出较大的流注直径,而在含氧量较小时则呈现出较多类似于树枝状的放电细丝[20].
本文计算分析了氮氧混合比对电子的输运系数的影响,如图4所示.由图4(a)可以看出,在低电场区,电子迁移系数随含氧量的增加而增大,而在高电场区含氧量对电子迁移率的影响较小;电子能量在电场小于100 Td时呈现出交错变化(见图4(b)),这主要是由于电子的主要碰撞类型由弹性碰撞向非弹性激发碰撞转变造成的,在电场较高时(>200 Td),气体混合比对电子能量的影响基本可忽略;由图4(c)和图4(d)可看出,在电场低于10 Td时,气体混合比例对电子扩散系数的影响较小,且纵向和横向扩散系数基本一致,而在电场大于10 Td后,电子扩散系数含氧量的增加而增大,并且横向扩散系数要显著大于纵向,在流注放电的流体模型中应注意区分;由于氧气的电离能比氮气要小,因此电离系数随着含氧量的增加而增大,见图4(e).

图4 (网刊彩色)氮氧气体混合比对电子通量输运系数的影响Fig.4.(color online)Variation of the electron fl ux transport coefficients with reduced electric fi elds for various N2-O2mixtures.
3.3 三体碰撞吸附对电子输运系数的影响
需要指出的是,当电负性气体存在时,低能电子与其之间的吸附作用是必须要考虑的一个重要因素.以纯氧为例,在BOLSIG+以及METHES中,基本忽略了三体碰撞吸附效应:e−+O2+O2→O−2+O2,其电子的损失主要通过附着解离(dissociative attachment)进行,即e−+O2→O−+O.通常情况下,三体碰撞吸附与气体密度与电场大小有关.对纯氧而言,气体密度增加,三体碰撞吸附增强进而电子损失加剧;电场增加,电子能量增大,而氧气的三体碰撞吸附截面随电子能量增加而减少,因此三体碰撞减弱,电子吸附损失降低.而附着解离与压强无关,氧气中附着解离效应仅随电场的增大而增强[19].图5给出了本模型计算得到的大气压下纯氧中三体碰撞吸附效应对电子通量输运系数的影响.可以看出,在低电场时(E/n0<10 Td),三体碰撞吸附对电子输运系数的影响较大、不可忽略.因此,由METHES和BOLSIG+所计算得到的电子通量传输系数仅仅适用于压强较低或者电场较大,从而附着解离占主导地位的情形,这也是使用METHES和BOLSIG+计算电负性气体中电子输运系数的又一个缺陷.

图5 大气压下纯氧中三体碰撞吸附对电子通量输运系数的影响Fig.5.Variation of the electron fl ux transport coefficients due to the three-body attachment in atmospheric pure O2.

图6 (网刊彩色)大气压下三体碰撞吸附对电子体及通量漂移速度的影响Fig.6.(color online)In fl uence of the three-body attachment on the electron transport coefficients in atmospheric pressure.
另外,若考虑三体碰撞吸附的影响,氧气中电子的体漂移速度和通量漂移速度差别也较大,见图6.通常来说,吸附可引起电子能量以及体漂移速度的增大或者减少,称为吸附加热(attachment heating)或者吸附冷却(attachment cooling).如图6所示,对氧气而言,在E/n0<0.7 Td时,电子的体漂移速度要小于通量漂移速度,因为在此范围内三体碰撞吸附主要为头部能量相对较大的电子,从而降低了整体的电子能量和速度,即吸附冷却;在0.7 Td<E/n0<20 Td范围内,电子体漂移速度要大于通量漂移速度,因为此时发生吸附的主要为尾部能量较低的电子,电子能量和体漂移速度增加,即吸附加热效应发生;在20 Td<E/n0<200 Td范围内,电子体和通量漂移速度基本一致,因为此范围内由电离碰撞消耗的头部高能量电子和三体碰撞吸附消耗的尾部低能量电子基本抵消;而在E/n0>200 Td时,电子体漂移速度又大于通量漂移速度,这主要是由于高电场下高能量电子大量增加,电离碰撞消耗的头部高能量电子比较于尾部被吸附的低能量电子较少造成的.需要说明的是,在非电负性气体中,由于无吸附效应,因此在电场小于击穿电压时体和通量漂移速度是一致的;然而,当电场大于击穿电场并逐渐升高时,其体漂移速度也逐渐高于通量漂移速度.
3.4 流注放电仿真示例
为了进一步说明电子输运系数精确度对模拟结果的影响,采用流体模型对大气压下氮气中流注放电进行了一维仿真,并与一维PIC/MCC模拟结果进行比较.所采用的流体和粒子仿真模型见文献[21].如图7所示,流体模型和粒子模型采用相同的初始条件:初始电子数密度呈高斯分布,最大值为1015m−3;背景电场取6×106V/m,气体压强为105Pa,温度为293 K.

图7 初始电子数数密度分布Fig.7.Initial electron number distribution.
图8给出了电子数密度以及电场在不同时刻随空间位置的变化.流体模型中电子的输运系数分别由BOLSIG+以及本文模型计算获得.比较粒子模拟和流体模拟结果可知:随着时间的增长,最大电子数密度由初始时刻的1015m−3增大到约4 ns时的3×1018m−3,放电逐渐由电子崩发展为负流注放电,且流注通道内部电场逐渐降低;流体模拟和粒子模拟所得到的电子数密度和电场分布曲线变化趋势基本相同,在流注通道内部,使用本文模型计算得到的电子输运系数可以获得和粒子模拟基本一致的电子数密度及电场分布,而采用BOLSIG+中的电子输运系数则结果相差较大,很好地体现了准确电子输运系数的重要性;另外可以看出,粒子模拟中流注传播速度比流体模拟中稍大,且在流注头部区域,流体模拟得到的电子数密度与粒子模拟仍有不小的差异,其原因主要是由于流体模型中电子输运系数为局部区域电场的函数,而在流注头部敏感区域电场变化较小,电子数密度以及能量的变化却较为显著,已有的研究表明,若在流体方程中耦合电子数密度梯度的变化,可显著改善流体仿真的精确度[22,23].

图8 (网刊彩色)电子数密度以及电场强度在不同时刻随空间位置的变化Fig.8.(color online)Temporal evolution of the electron number density and the electric fi eld as a function of the spatial position.
4 结 论
本文采用自主开发的蒙特卡罗模型求解低温等离子体中的电子输运系数,研究了氮氧气体混合比以及三体碰撞吸附对电子输运系数的影响,并在氮气流注放电一维仿真中测试电子输运系数的重要性.主要结论如下:
1)比较本模型以及现有工具BOLSIG+和METHES所得到的电子输运系数和其他参数,验证了本模型的正确性和精确性;而基于两项近似的BOLSIG+则在高电场时误差较大;
2)本模型可以方便获取任意气体混合比中的电子输运数据,且研究表明,氮氧混合比对电子输运系数的影响较大,轴向和横向扩散系数差异显著,在实际流体仿真时应予以区分;
3)在气体压强较高时,电子与电负性气体分子的三体碰撞吸附对电子的体和通量输运系数影响均较大,而BOLSIG+和METHES中未充分考虑此因素,因此其适用范围受限;
4)氮气中流注放电的一维仿真表明,采用本模型改进精度后的电子输运系数可以显著改善流注通道内电子数密度和电场仿真结果与粒子模拟结果的符合度,而在流注头部与粒子仿真还存在差异,分析其原因是由于本模型中电子输运系数仅表示为局部电场的函数,未考虑流注头部的电子数密度梯度造成的,还有待于后期进一步研究.
[1]RaizerYP1991GasDischargePhysics(Berlin:Springer)pp324–343
[2]Ebert U,Sentman D 2008J.Phys.D:Appl.Phys.41 230301
[3]Ebert U,Nijdam S,Li C,Luque A,Briels T,van Veldhuizen E 2010J.Geophys.Res.115 A7
[4]Shao T,Yan P 2015Atmospheric Gas Discharge and Its Plasma Applications(Beijing:Science Press)pp385–611(in Chinese)[邵涛,严萍2015大气压气体放电及其等离子体应用 (北京:科学出版社)第385—611页]
[5]Li C,Teunissen J,Nool M,Hundsdorfer W,Ebert U 2012Plasma Sources Sci.Technol.21 055019
[6]Li C,Ebert U,Hundsdorfer W 2012J.Comput.Phys.231 1020
[7]www.bolsig.laplace.univ-tlse.fr version:07/2015[2017-6-13]
[8]Biagi S F 1999Nucl.Instrum.Methods A421 234
[9]Bankovic A,Dujko S,White R D,Buckman S J,Petrovic A L 2012Eur.Phys.J.D66 174
[10]Rabie M,Franck C M 2016Comput.Phys.Commun.203 268
[11]http://lxcatnet[2017-6-13]
[12]Sun A B,Becker M M,Lo ff hagen D 2016Comput.Phys.Commun.206 35
[13]Sun A B,Teunissen J,Ebert U 2013Geophys.Res.Lett.40 2417
[14]Sun A B,Teunissen J,Ebert U 2014J.Phys.D:Appl.Phys.47 445205
[15]Lippert R A,Bowers K J,Dror R O,Eastwood M P,Gregersen B A,Klepeis J L,Kolossvary I,Shaw D E 2007J.Chem.Phys.126 046101
[16]Birdsall C K 1991IEEE Trans.Plasma Sci.19 65
[17]Yous fiM,Hennad A,Alkaa A 1994Phys.Rev.E9 4
[18]Bošnjaković D,Petrovic Z L,White R D,Dujko S 2014J.Phys.D:Appl.Phys.47 435203
[19]Dujko S,Ebert U,White R D,Petrovic Z L 2011Jpn.J.Appl.Phys.50 08JC01
[20]Wormeester G,Pancheshnyi S,Luque A,Nijdam S,Ebert U 2010J.Phys.D:Appl.Phys.43 505201
[21]Teunissen J,Sun A B,Ebert U 2014J.Phys.D:Appl.Phys.47 365203
[22]Li C,Brok W J M,Ebert U,van der Mullen J J A M 2007J.Appl.Phys.101 123305
[23]Li C,Ebert U,Hundsdorfer W 2010J.Comput.Phys.229 200
Monte Carlo simulations of electron transport coefficients in low temperature streamer discharge plasmas∗
Sun An-Bang†Li Han-WeiXu Peng Zhang Guan-Jun
(State Key Laboratory of Electrical Insulation and Power Equipment,Xi’an Jiaotong University,Xi’an 710049,China)
Streamer is usually present at the initial stage of atmospheric pressure air discharge,which occurs in nature as a precursor to lightning,transient luminous events in upper atmosphere and has much potential applications in industry,such as the treatment of polluted gases/liquids,assisted combustion,plasma enhanced deposition etc.Streamer is a multi-scale problem both in time and in space,which brings much difficulty to the conventional diagnostic approaches.In past decades, fl uid or particle- fl uid hybrid models have been frequently used for understanding the mechanisms of streamer discharges because of their high efficiencies of calculations.Accuracies of the electron transport coefficients(including drift/di ff usion coefficient,ionization/attachment coefficient,electron mean energy and extra)play a key role in ensuring the correctness of the fl uid or hybrid simulations.As far as we know,BOLSIG+and MAGBOLTZ are two typical tools for obtaining the electron transport coefficients and have been widely utilized in previous models.BOLSIG+uses“two-term”approximation which is not sufficient for some molecular gases,MAGBOLTZ cannot calculate the bulk transport coefficients:these data are required for some models.METHES is an additional tool for computing electron transport coefficients,however,speci fi c platform is required which is not very user-friendly.As sorts of drawbacks exist in currently available calculating tools,in the paper,a Monte Carlo model is developed for computing the electron transport coefficients in gases,the model is fl exible to choose any type of gas mixture and its accuracy has been validated by comparing with BOLSIG+and METHES.Furthermore,the in fl uences of N2-O2mixture and three-body attachment process in high gas pressures on the transport coefficient are investigated.It is worth mentioning that three-body attachment process can signi fi cantly change the electron transport properties at a relatively low reduced electric fi eld.Thus,speci fi c attention must be paid to the transport coefficients if simulation is performed at a high pressure.In addition,di ff erences between the bulk and fl ux coefficients are analyzed which are not distinguished in some previous models.Finally,we further validate the present Monte Carlo model by performing simulation of streamer discharge in atmospheric N2,which shows that the improved electron transport coefficient from our Monte Carlo model can improve the simulated plasma properties,in particular at the interior of the streamer channel.The existence of divergence at the tip of the streamer channel might be due to our local fi eld approximation;if a density gradient term is included in the impact ionization term and local electron energy approximation of the electron transport coefficients is used,the accuracy of the fl uid can be improved further.
streamer,low temperature plasma,electron transport coefficient,Monte Carlo model
13 June 2017;revised manuscript
17 July 2017)
(2017年6月13日收到;2017年7月17日收到修改稿)
10.7498/aps.66.195101
∗国家自然科学基金(批准号:51777164)、西安交通大学“青年拔尖人才支持计划”(批准号:DQ1J008)、电力设备电气绝缘国家重点实验室(批准号:EIPE17311)和中央高校基本科研业务费专项资金(批准号:1191329723)资助的课题.
†通信作者.E-mail:anbang.sun@xjtu.edu.cn
©2017中国物理学会Chinese Physical Society
PACS:51.10.+y,51.50.+v,31.15.–p
10.7498/aps.66.195101
*Project supported by the National Natural Science Foundation of China(Grant No.51777164),the “Young Talent Plan”of Xi’an Jiaotong University,China(Grant No.DQ1J008),State Key Laboratory of Electrical Insulation and Power Equipment,China(Grant No.EIPE17311),and the Fundamental Research Funds for the Central Universities,China(Grant No.1191329723).
†Corresponding author.E-mail:anbang.sun@xjtu.edu.cn

