地图比例尺定义及多比例尺地图覆盖的拓扑学原理
张瑞辰,钟业勋,胡宝清,刘雁春,边少锋
(1. 海军工程大学 导航工程系,湖北 武汉 430043; 2. 广西师范学院 北部湾环境演变与资源利用省部共建教育部重点实验室;广西地表过程与智能模拟重点实验室,广西 南宁 530001; 3. 广西测绘地理信息局,广西 南宁 530023;4. 海军大连舰艇学院,辽宁 大连 116018)
地图比例尺定义及多比例尺地图覆盖的拓扑学原理
张瑞辰1,钟业勋1,2,3,胡宝清2,刘雁春4,边少锋1
(1. 海军工程大学 导航工程系,湖北 武汉 430043; 2. 广西师范学院 北部湾环境演变与资源利用省部共建教育部重点实验室;广西地表过程与智能模拟重点实验室,广西 南宁 530001; 3. 广西测绘地理信息局,广西 南宁 530023;4. 海军大连舰艇学院,辽宁 大连 116018)
为了用数学形式表征地图比例尺的本质特征,地图比例尺的概念需要精密的数学表达形式。根据地图比例尺与地球制图半径、可视化点对应点元半径的函数关系,给出两个地图比例尺的数学定义;由函数的定义域推出大、中、小地图比例尺的分类;并从拓扑学覆盖的数学定义,论证制图区域多种地图比例尺覆盖的科学合理性。
地图比例尺;地球半径;可视化点;点元半径;数学定义;覆盖
比较法是不可或缺的认知与描述工具,更是解释性的,是一项控制变异的方法(Smelser,1976)及建立变量间普遍关系或“法则”的方法(Lijphart,1971;Sartori,1970),最终,它是一项归纳推理的方法。有的学者认为,没有比较就没有科学思想(Swanson,1971),且无论何种形态的研究,都不可避免是比较性的(Lasswell,1986;Liebeerson,1985)。比较构成了所有科学解释的核心(Armer,1973;Bailey,1982;Blalock,1961),所有科学本质上都是比较的(Klingman,1980)[1]。地图作为人们空间认知的必要工具,比较法的使用更是比比皆是:地物的结构特征、外在形态、地物的大小、数量、距离远近、分布密度等等,都需要比较才能得出判断结论。地物的定位精度、地物的概括程度也是一种比较,这类比较与比例尺相关,这就涉及地图按比例尺的分类。关于地图按比例尺的分类,传统的教科书中通常分为3类:大比例尺地图:1∶10万及更大比例尺地图;中比例尺地图:介于1∶10万和1∶100万之间的地图;小比例尺地图:1∶100万及更小比例尺的地图[2-3]。关于地图比例尺,普遍认同的定义是:地图上两点之间的距离与实地两对应点之间的距离的比值。然而,由于地球表面是个不可展面,地图投影就是地球表面在平面上的拓扑变换。拓扑变换的双一一函数关系,使得不可展面上的线素投影到平面上也必须是连续的,这就使平面上的线必定有重叠或拉伸,也就是说,从严格的意义上,地图上不同部位的比例尺是不相同的,这就是局部比例尺。地图上不同部位的两点距离的变异性导致以它推出的地图比例尺具有不确定性。确定性是科学思维的一个基本规定,科学思维的精密性在于用数学形式表征事物的本质特征[4]。确定性要求地图比例尺必定是某个有规律的变量的函数,并且存在对所有地图都不变的常数。基于此思路,本文根据制图时采用的地球半径和可视化点对应的点元半径与地图比例尺的函数关系,推导了两个地图比例尺的数学定义。还从拓扑学中的覆盖定义,阐释了多种比例尺地图对制图区域的覆盖原理。
1 基于地球制图半径函数的地图比例尺的数学定义
计算地图投影或制作地图时,必须将地球(椭球或球)按一定的比例缩小并表示在平面上,这个比率称为地图的主比例尺,或称普通比例尺。地图上标注的比例尺就是主比例尺[5-6]。地球制图半径与地图比例尺的密切相关性可以视地图比例尺为地球制图半径的函数,构建地图比例尺的通用公式,并通过制图半径的定义域,给出大、中、小比例尺的数学定义。
1.1 地图比例尺的定义
定义1地图比例尺。设地球的实体半径为R,地图制图采用的球体半径为Rz,Rz与R之比称为地图主比例尺,简称地图比例尺,即
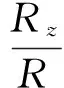
(1)
式中:地球的实体半径R为常数,Rz与地图比例尺M成正比关系。
设D为地图,M∈D,M的大小决定地图比例尺的分类:
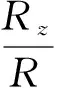
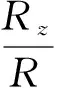
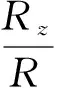
条件1)表明,大比例尺地图的比例尺M的定义域为1和1/100 000的半开区间,但不会等于1,因为不存在比例尺为1的地图;中比例尺地图的比例尺M的定义域为1/100 000到1/1 000 000的开区间;小比例尺地图的比例尺M的定义域为1/1 000 000到0的半开区间,说明没有比例尺为0的地图。
1.2 实例
例1设R为等面积球体半径,试求大、中、小比例尺地图所对应的制图球体半径Rz的定义域。
解:等面积球体半径R用式(2)求得。
(2)
式中:a为地球椭球长半径,e为第一偏心率。采用2000国家大地坐标系时,a=6 378 137 m,e=0.081 819 191,R=6 371 007 m,地球的实体半径R为常数。
1)Rz∈[63.710 07,6 371 007)⟺大比例尺地图;
2)Rz∈(6.371 007,63.710 07)⟺中比例尺地图;
3)Rz∈(0,6.371 007]⟺小比例尺地图。
因63.710 07 m正好是等面积地球的实体半径6 371 007 m的1/100 000,大于此值时为大比例尺地图。Rz的定义域表明,Rz不会与R相等,因为不存在比例尺为1:1的地图;当Rz为6.371 007 m时,正好是等面积地球的实体半径6 371 007 m的1/1 000 000,小于此值时比例尺更小,但不会等于0,不存在比例尺为0的地图,所以这类地图为小比例尺地图;而球体的制图半径处在6.371 007 m与63.710 07 m之间的地图属于中比例尺地图。
2 基于可视化点对应点元半径函数的地图比例尺的数学定义
2.1 地图可视化点的阈值及其对应的点元
F.泰勒在1994年提出的著名地图学概念图解中,把可视化看作地图学的核心。可视化在西方多称为视觉化(Visualization),解释为“不可直接觉察的某种事物的直观表示”。地学空间信息中,有可见的居民地、道路、水系、植被;有深埋地下的矿藏、地质构造,这些事物存在但不可见;有可测不可见的气温、气压,或明或隐的行政界线,以及人口、工农业产值等人文要素;有不可再现的历史事件和消亡现象等。但在地图上,这些不可直接觉察的事物,通过符号化表示使其实现了可视化[7-9]。不同比例尺的地图图式,规定了地图可视化的阈限:线粗为0.1 mm,点大为0.15 mm,符号间的间隔不能小于0.2 mm[10-11]。一个0.15 mm的可视化点,在不同比例尺条件下反演为实地上的点元—一个圆形区域。所谓点元,也就是把这样一个圆形区域仅看作0.15 mm的可视化点的对应物,圆形区域内的所有地物的性质,视为等价类[12-13]。
定义2地图可视化点对应的点元。设S为球面,Y为平面,存在拓扑映射f:S→Y,令P0=0.15 mm,如果C∈S∧C=πr2⟹f(C)=P0∈Y,则称C为可视化点P0=0.15 mm对应的点元。也即f-1(P0)=C=πr2。
2.2 基于点元半径函数的地图比例尺定义
由于任何比例尺地图上的可视化点P0=0.15 mm是不变的,同一比例尺地图上的点元大小相同,不同比例尺地图对应的点元大小不同,比例尺越小可视化点对应的点元越大,因此, 地图比例尺的大小可以用点元大小来度量,它是点元半径r的函数。
定义3地图比例尺。设可视化点P0=0.15 mm,把它视为一个圆点,它的半径r0=0.075 mm,令点元C的半径为rc,则地图D的比例尺M为
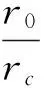
(3)
式中:r0为常数,地图比例尺M与点元C的半径rc成反比,rc愈小则地图比例尺愈大,反之亦然。
设D为地图,M∈D,M的大小决定地图比例尺的分类:
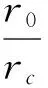
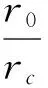
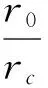
条件1)表明,没有比例尺为1的地图,条件3)表明,没有比例尺为0的地图。定义1和定义3是等价的地图比例尺定义。
3 多种比例尺地图覆盖同一地区的拓扑学原理
3.1 覆盖定义
定义4覆盖。令X表示一个随意的非空集合,又E表示X的一个子集。如果X的一个子集族{Uα}α∈I能使E⊂∪α∈IUα,则{Uα}α∈I叫做集合E的一个覆盖。当{Uα}α∈I是E的一个覆盖时,又说,E被所有的Uα所覆盖,或者说,所有的Uα覆盖着E。
令
u={Uα}α∈I,并令v={Uα}α∈I*,其中,I*∈I.
(4)
如此,称族v为族u的子族,并且可以写成v⊂u或者u⊃v。当E的一个覆盖u的某个子族v也是E的一个覆盖时,称v为u的一个子覆盖[14]。拓扑学中关于覆盖的定义,为测绘工作中对同一地区的不同比例尺地图覆盖提供了理论基础。
3.2 不同比例尺地图覆盖的理论阐释
在测绘工作中,常常在一个国家或一个省区,施测多种比例尺地图。我国的1∶100万、1∶50万、1∶25万、1∶10万地形图已全部覆盖了全国。图1为1∶100万、1∶50万、1∶25万比例尺覆盖原理的示意图,非常简洁地表示了多比例尺地图覆盖的数量和包含关系。
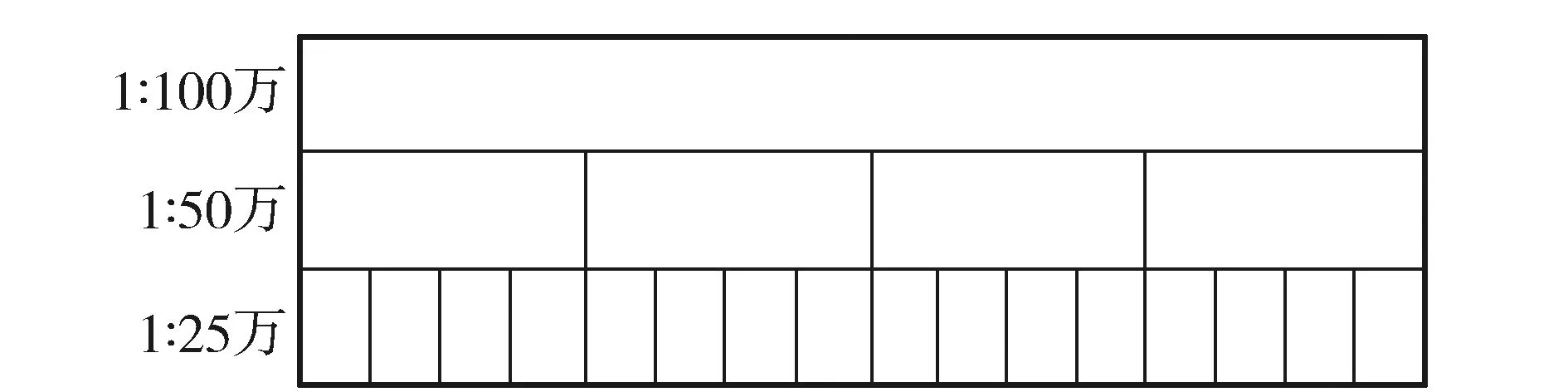
图1 多种比例尺地图覆盖
我国的1∶100万图77幅,1∶50万图257幅,1∶25万图819幅,1∶10万图7 176幅。1:5万覆盖全国图幅数应为24 091幅,已测制19 333幅,占80%。1∶1万地形图已测制14.6万幅,覆盖面积达422万km2。经济发达地区已测制了第三代1∶5万和1∶1万地形图[15]。设X为地球表面,E∈X为中国的陆地面积,在E⊂∪α∈IUα的包含关系中,当I=77⟹Uα⟺1∶100万地形图,此时u={Uα}α∈I⟹v={Uα}α∈I*∧u⊃v,表明1∶100万地形图包含的子集族有v,v可为1∶50万、1∶25万、1∶10万、1∶5万、1∶2.5万、1∶1万和1∶5 000地形图,这些不同比例尺的子集族,全都是中国的陆地面积E∈X的覆盖。
4 结 论
地图比例尺是地图制图中的基本概念,它的产生是比较法应用的结果,而地图比例尺又是反演地物状态的依据和尺度,与比较法密切相关。根据地图比例尺必定是某个有规律的变量的函数的科学思维的确定性要求,提出了地图比例尺的两种数学形式:地球制图半径函数式和点元半径函数式。前者以地球实体半径R为常数,地图比例尺与地球制图半径Rz成正比;后者以可视化点P0=0.15 mm为常数,地图比例尺与点元半径rc成反比。这两个地图比例尺公式是等价的。地图比例尺的点元半径函数式是本文的创新公式。由于社会经济发展的程度、技术条件等因素,我国和各省(区)国家基本比例尺地图覆盖的情况有所差异。总的情况是,经济发达人口较多的东部地区,不但覆盖了各种比例尺地图,有的还测制了第三代1∶5万和1∶1万地形图。本文根据拓扑学中覆盖的定义,对多种比例尺地图覆盖同一地区的现象进行了阐释。
[1] [瑞士]丹尼尔.卡拉曼尼(Daniele Caramani).基于布尔代数的比较法导论[M].蒋勤,译.上海:格致出版社,上海人民出版社,2012.
[2] 祝国瑞.地图学[M].武汉:武汉大学出版社,2004.
[3] 廖克.现代地图学[M]. 北京:科学出版社,2003.
[4] 周昌忠.科学思维学[M]. 上海:上海人民出版社,1988.
[5] 胡毓钜.龚剑文.地图投影[M].2版.北京:测绘出版社,2006.
[6] 胡毓钜.数学制图学[M].北京:中国工业出版社,1964.
[7] 钟业勋.数理地图学[M].北京:测绘出版社,2007.
[8] 钟业勋,童新华.基于可视化的地图学概念的形成逻辑[J].海洋测绘,2012,32(4)∶78-80.
[9] 钟业勋,朱重光,童新华,等.地图可视化与地图学概念的相关性研究 [J].玉林师范学院学报(自然科学版),2012,33(2)∶146-149.
[10] 国家技术监督局.1∶25 000,1∶50 000,1∶100 000地形图图式[S]. 北京:中国标准出版社,1991.
[11] 钟业勋,胡宝清,童新华,等. 地图学概念的数学表述研究[M].北京:科学出版社,2015.
[12] 李占元, 钟业勋.等高线悖论与广义等高线定义的研究[J].测绘科学,2005,3(4):25-26.
[13] 钟业勋,黄仁涛,王龙波.等高线悖论与广义等高线定义的修改[J].黑龙江工程学院学报(自然科学版),2007,21(3):4-6.
[14] 李孝传,陈玉清.一般拓扑学导引[M].北京:高等教育出版社,1982.
[15] 百度知道.国家基本比例尺地图的全中国图幅总数量[DB/OL].Kongfz.com 孔夫子旧书网,[2016-06-01].
[责任编辑:郝丽英]
Coverage in the cartographic region
ZHANG Ruichen1,ZHONG Yexun1,2,3,HU Baoqing2,BIAN Shaofeng1
(1. Dept. of Navigation Engineering, Naval University of Engineering, Hubei 430033,China; 2. Key Laboratory of Beibu Gulf Environment Change and Resources Use, Ministry of Education, Guangxi Teachers Education University, Nanning 530001,China; 3. Guangxi Key Laboratory of Earth Surface Processes and Intelligent Simulation, Guangxi Teachers Education University, Nanning 530001,China; 3. Guangxi Regional Geographical Information Bureau of Surveying and Mapping, Nanning 530023,China; 4. Dalian Naval Academy, Dalian 116018,China)
In order to express the essential features of map scale in mathematical form, the concept of map scale needs a precise mathematical expression form. According to the relationships between map scale and earth mapping radius as well as visualization point’s corresponding point element radius, the paper gives two mathematical definitions of the map scale. From the domain of the function it introduces the classification of large, medium and small scale maps. From the mathematical definition of topology coverage, the paper demonstrates the scientific rationality of various map scale coverage in the cartographic region.
map scale; earth radius; visualization point; radius of point element; mathematical definition; coverage
P22
A
1671-4679(2017)05-0017-04
2017-05-25
国家自然科学基金项目(20154424,41671459,41361022,41571441);广西科技开发项目(2014DD29090);广西北部湾重大基础专项子课题(2012GXNSFEA053001)
张瑞辰(1993-),女,硕士研究生,研究方向:海图投影.
10.19352/j.cnki.issn1671-4679.2017.05.004

