时域衰减信号的复合材料叶片阻尼不确定性测试

梁晓龙，李 晖，牛 义，周正学

(东北大学 机械工程与自动化学院，沈阳 110819)

时域衰减信号的复合材料叶片阻尼不确定性测试

梁晓龙，李 晖，牛 义，周正学

(东北大学 机械工程与自动化学院，沈阳 110819)

基于复合材料叶片的时域衰减信号，对其阻尼的不确定性进行测试研究。首先，组建复合材料叶片的阻尼测试系统，提出具体的阻尼不确定性测试流程，并通过“标准差”指标来量化表征某一阶阻尼的不确定性程度；然后，以三种不同类型的TC500碳纤维/树脂基复合材料直板叶片为研究对象，通过测试获取其在不同衰减时刻的阻尼结果，并证明其阻尼确实存在不确定性现象；最后，讨论激励幅度、边界条件、背景噪声对复合材料叶片某一阶阻尼不确定性的影响程度和影响规律，并提出采用线性平均法来准确获得其阻尼结果。

振动与波；时域衰减信号；复合材料叶片；阻尼；不确定性测试；影响因素分析

复合材料叶片广泛应用于工程实际中，如太阳能帆板、航空发动机风扇叶片以及大型风力机叶片等[1–3],随着它们的结构越来越复杂、工作环境越来越苛刻，其振动问题也越来越突出，由此引发的振动超标、磨损、疲劳失效等故障问题也越来越突出[4–7]。在复合结构系统的振动和噪声控制中，阻尼特性由于可以客观反映结构系统振动过程中能量耗散的快慢程度，因而得到了越来越多工程技术人员的重视。但由于复合材料叶片结构阻尼机理的复杂性[8]，例如，其阻尼参数可能会受到复合材料中增强相与基体的界面强度、边界约束条件、激励幅度、背景噪声及环境温度等因素的影响[9–10]，使阻尼的测量及评价具有很大程度的不确定性。因此，关于复合材料叶片阻尼测试的研究还应进一步深入。

目前，用于描述复合材料叶片阻尼的阻尼参量有很多，包括相位差角、对数衰减系数、品质因子、损耗因子等[11]。人们一般通过时、频域两类阻尼测试方法来获取复合材料叶片阻尼参数。例如，Mahi和Assarar对复合材料悬臂梁的阻尼特性进行了测试，发现复合梁结构在不同的激振频率下表现出不同的阻尼值[12]。Crane和Gillespie搭建脉冲激励实验台，对三类不同材料复合梁试件的损耗因子进行了测试，研究发现90°纤维复合梁的阻尼性能要优于0°纤维复合梁[13]。Berthelot和Sefrani利用锤击法获得芳纶纤维和玻璃纤维两种复合梁结构的频响函数，并获得了模态损耗因子等参数[14]。Botelho等也利用自由振动衰减法测试出碳纤维材料各阶模态的固有频率和阻尼比[15]。Sum Nam Jung等人通过应变能损耗计算出复合材料叶片结构的阻尼比[16]。Kostopoulos和Korontzis通过自由振动衰减法获得了碳纤维/树脂复合悬臂梁的阻尼参数，并发现了该类型复合结构的阻尼与激振频率存在非线性的依赖关系[17]。李典森等人通过时域衰减信号获得了三维编复合材料悬臂梁结构的阻尼比及损耗因子，并得出结论三维编织复合材料的阻尼性能随编织纤维角的增大、纤维体积含量的降低而提高[18]。杨强等人对某航空发动机复合材料叶片进行了模态测试，通过最小二乘复指数法获得复合材料叶片结构的频率、振型及阻尼[19]。杨云昭等人对碳纤维梁结构的阻尼特性也进行了测试，研究发现损耗因子随着铺层角度的增大而增大，且随着振动频率变化，在某一频率下达到最大的损耗因子[20]。倪楠楠和温月芳等人通过实验测试了无纺布/环氧树脂复合材料悬臂梁结构的共振频率及自由振动衰减曲线并计算了其损耗因子[21]。

从当前可掌握的文献资料来看，国内外研究人员针对复合材料叶片结构的阻尼特性开展了大量的研究工作，但许多文献在采用包络线或对数衰减法获取阻尼时，并没有考虑时域衰减信号的不同衰减时刻对阻尼参数的影响。同时，笔者在测试实践中还发现复合材料叶片的阻尼会受到激励幅度、边界条件、环境温度等因素的影响，其振动衰减信号也很容易受到背景噪声的干扰。由此可见，基于时域衰减信号获得复合材料叶片阻尼具有很大的不确定性，因此，有必要对该问题进行更深入的研究。

本文基于复合材料叶片的时域衰减信号，对其阻尼的不确定性进行了测试研究。首先，组建了复合材料叶片的阻尼测试系统，提出了具体的阻尼不确定性测试流程，并通过“标准差”指标来量化表征某1阶阻尼的不确定性程度；然后，以三种不同类型的TC 500碳纤维/树脂基复合材料直板叶片为研究对象，通过测试获取其在不同衰减时刻的阻尼结果，并证明其阻尼确实存在不确定性现象；最后，讨论了激励幅度、边界条件、背景噪声对复合材料叶片某1阶阻尼的不确定性的影响程度和影响规律，并提出了采用线性平均法来准确获得其阻尼结果。

1 复合材料叶片阻尼测试系统

1.1 测试研究对象

本文面向复合材料直板叶片，基于时域衰减信号进行阻尼不确定性测试，实验对象分别为A、B、C三种不同类型的复合材料直板叶片，其实物图如图1所示。

图1 三种不同类型的复合材料直板叶片

A、B、C型复合材料叶片均由TC 500碳纤维/树脂基复合材料制作而成，每个铺层具有相同的厚度和纤维体积分数；它们的长、宽、厚尺寸均为230 mm×130 mm×2.36 mm。其中，A型叶片为对称正交铺设，即[(0°、0°、90°、90°)5、0°]，铺层共有21层；B型叶片为编织铺设，编织角为+45°/-45°，共有12层；C型叶片也为编织铺设，编织角为+90°/0°，铺层共有12层。

1.2 测试系统

为了精确有效地获取复合材料叶片的阻尼参数，笔者采用模态力锤来对其进行脉冲激励，利用金盾电磁振动台对其进行扫频和定频激励，并通过非接触激光测振仪来获取其振动响应信号。同时，使用LMS数据采集仪和移动工作站对激励信号和响应信号进行实时采集和分析处理。图2给出了获取复合材料叶片阻尼时所搭建的测试系统，表1给出了测试系统中各部分仪器及传感器的具体型号。

图2 复合材料叶片阻尼测试系统

2 复合材料叶片阻尼不确定性测试流程

基于时域衰减信号进行复合材料叶片阻尼不确定性测试，首先要获得复合材料叶片的各阶固有频率，此步骤可以通过锤击法获得其各阶固有频率的大致范围，再利用振动台对其进行扫频激励准确获取各阶固有频率。然后，采用定频共振激励待复合材料叶片达到稳态响应后停止激励，并用非接触激光测振仪测量时域衰减信号。最后，通过包络线法获得该信号在不同衰减时刻对应的阻尼比，并对其不确定性进行评价。测试流程共包括以下几个关键步骤：

表1 复合材料叶片阻尼测试相关仪器

（1）确定测试所需的边界条件及测点的位置

为了模拟复合材料直板叶片在叶盘上的装配方式，测试采用悬臂约束边界条件。首先将复合材料叶片通过夹具固定在激振工作台上，并通过力矩扳手来确定其夹具上夹紧螺栓的力矩值，应以统一规定的力矩来拧紧A、B、C型叶片进行测试。约束后的直板叶片的长、宽、厚尺寸均为200 mm×130 mm×2.36 mm。接下来进行测点位置的确定，经过反复测试对比，为了使振动响应较强又不超出激光测振仪的量程，测点位置选取在距离直板叶片约束端190 mm，且距离右侧自由边20 mm处。

（2）通过锤击法初步获得复合材料叶片固有频率

使用模态力锤对复合材料叶片进行脉冲激励并获得力信号，同时使用非接触激光测振仪获得响应信号。通过LMS软件分析出频响函数峰值所对应的频率，初步获得复合材料叶片的固有频率。

（3）通过扫频法精确获得复合材料叶片固有频率

用振动台以基础激励的方式对悬臂复合材料叶片结构进行定幅扫频激励，扫频区间可以选择为锤击获得的某阶固有频率的75%～125%，在此频段内以能够有效消除瞬态振动的扫频速度进行扫频测试（通常小于1 Hz/s）；用激光测振仪进行响应信号的采集，并对时域原始数据进行分时段FFT变换处理，通过辨识响应峰值来精确识别复合材料叶片的各阶固有频率。

（4）获取时域衰减信号

在精确获得复合材料叶片各阶固有频率的基础上，用振动台以某阶固有频率定频、定幅激励复合材料叶片；待结构达到稳态响应后停止激励，同时使用激光测振仪记录该阶固有频率激励下的时域衰减信号。

（5）通过包络线法获得阻尼

由于测试时，复合材料叶片时域衰减信号的总衰减时长并不相同（受到激励幅度、模态阶次、边界条件等因素的影响），为了方便比对阻尼测试结果，分别设定了四个固定的衰减时刻t1、t2、t3、t4，并在上述四个衰减时刻通过包络线法获得复合材料叶片的阻尼结果。图3给出了某次测试获得的不同衰减时刻对应的包络线图，此时t1、t2、t3、t4，分别设定为0.25 s，0.5 s，0.75 s，1 s，不同衰减时刻所对应的包络线分别为l1、l2、l3、l4。

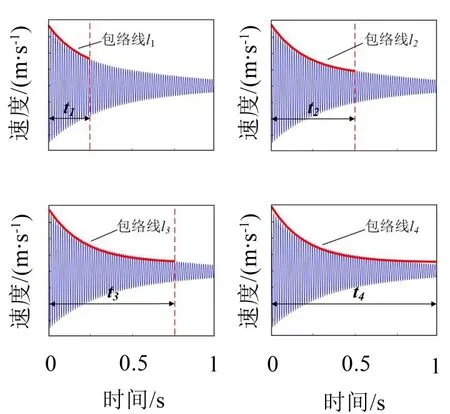
图3 复合材料叶片衰减信号在不同衰减时刻的包络线图

（6）对复合材料叶片的阻尼不确定性进行评价在四个固定的衰减时刻t1、t2、t3、t4，通过包络线法获得了复合材料叶片在某1阶模态的阻尼比ξ1，ξ2，ξ3，ξ4之后，通过线性平均方法，将上述4个阻尼结果的平均值作为最终的某阶模态阻尼结果。进一步，求取上述4个衰减时刻对应阻尼比的标准差，来量化表征某1阶阻尼不确定性的程度，以便可以科学地评价其阻尼的不确定性。其中4个衰减时刻对应阻尼比的标准差s表达式为

式中ξi为在固定衰减时刻ti通过包络线法获得的某1阶模态的阻尼比，ξavg为4个固定衰减时刻对应的阻尼比的平均值。

3 阻尼不确定性测试结果确认

3.1 A型复合材料直板叶片不确定性测试结果

通过1.2部分搭建的测试系统，按照2中所提出的测试流程对A型复合材料直板叶片进行测试，测试所获得的前6阶固有频率如表2所示。

然后，获取A型复合材料直板叶片在不同衰减时刻对应的阻尼参数，其中4个固定的衰减时刻t1、t2、t3、t4分别设定为0.25 s，0.5 s，0.75 s，1 s。为证明A型叶片阻尼的不确定性是客观存在的，对A型叶片进行三次重复测试。

表2 A型复合材料直板叶片前6阶固有频率/Hz

表3、表4、表5给出了三次测试中A型叶片在不同衰减时刻辨识出的阻尼结果及其标准差。图4则给出了A型叶片的前6阶模态在不同衰减时刻所对应的阻尼比（图中的阻尼比为三次测试结果的平均值）。

图4 A型叶片前6阶模态在不同衰减时刻对应的阻尼比

根据A型叶片的三次阻尼测试结果可以看出，其各阶阻尼对应的标准差位于0.48%～10.63%之间。因此，可知由于所选衰减时刻的差异，确实会产生阻尼结果的不确定性。同时，三次测试获得的阻尼结果和标准差都比较接近，更加证明了A型叶片阻尼不确定性的存在不是偶然现象。

3.2 B型和C型叶片阻尼不确定性测试结果

上述的测试说明了A型叶片基于时域衰减信号获得的阻尼具有不确定性。对于其它类型复合材料叶片的阻尼是否也具有这样的不确定性，笔者选取与A型叶片不同类型的B、C型叶片，同样通过1.2部分搭建的测试系统，按照2中所提出的测试流程对其各进行一次测试并比对。表6、表7给出了B型叶片和C型叶片在不同衰减时刻辨识出的阻尼结果及其标准差。

根据B型叶片和C型叶片的测试结果可以看出，他们在不同衰减时刻ti获得的阻尼比不相同，其各阶的阻尼比对应的标准差在0.55%～6.20%之间，进一步说明，基于时域衰减信号所获得的复合材料叶片阻尼均具有不确定性。

4 复合材料叶片阻尼不确定性的影响因素分析

表3 A型叶片第一次阻尼测试结果及其标准差

表4 A型叶片第二次阻尼测试结果及其标准差

表5 A型叶片第三次阻尼测试结果及其标准差

以A型叶片作为实验对象，详细讨论激励幅度、边界约束条件及背景噪声等因素对其阻尼不确定性的影响规律。

表6 B型复合材料叶片的阻尼测试结果及其标准差

表7 C型复合材料叶片的阻尼测试结果及其标准差

4.1 激励幅度

选取1 g、2 g、4 g、6 g四个激励幅度，以A型叶片的第3阶固有频率对其进行定频激励，待达到稳态响应后停止激励，获取其时域衰减信号。表8给出了该信号在不同衰减时刻所对应的第3阶阻尼比及其标准差，图5还给出了不同激励幅度下其阻尼的变化曲线（其中4个不同的衰减时间t1、t2、t3、t4分别设定为0.25 s，0.5 s，0.75 s，1 s）。

表8 不同激励幅度下A型叶片第3阶阻尼比及其标准差

对上述结果进行分析可知，A型叶片第3阶阻尼比的标准差位于1.25%～2.59%之间，且随着激励幅度的增加，其阻尼的不确定性程度在逐渐增大。同时，随着衰减时间的持续和激励幅度的减小，其阻尼结果呈现出逐步增大的趋势，这种现象是由于复合材料叶片的阻尼具有振幅依赖性所造成的。后续有必要针对这种非线性现象，从理论上建立其非线性阻尼模型，进一步解释其非线性变化的能量耗散机理。

4.2 边界条件

首先，使用50 Nm的力矩来拧紧A型叶片夹具上的四个M8螺栓，并通过力矩扳手来调整螺栓的拧紧力矩值，以模拟不同边界条件的变化。然后，分别在螺栓100%、75%、50%、25%拧紧条件下，依次按照2中所提出的测试流程进行阻尼测试。表9则给出了不同边界条件下A型叶片第3阶阻尼结果及其标准差。

图5 A型叶片在不同激励幅度下的第3阶阻尼变化曲线

表9 不同边界条件下A型叶片第3阶阻尼比及其标准差

根据A型叶片在不同边界条件下的测试结果可以看出，其第3阶阻尼比的标准差在1.89%～3.83%之间。且随着边界条件约束能力变差，其标准差也逐渐减小，即阻尼的不确定性程度在逐步减小。这可能是由于边界条件的弱化导致阻尼性能降低，因而在不同的衰减时刻，A型叶片对应的阻尼结果的差别变小。

4.3 背景噪声

在测试中发现复合材料叶片的时域衰减信号很容易受到背景噪声的干扰，因此讨论背景噪声对其阻尼不确定性的影响，在1.2部分搭建的测试系统中，增加了高压空气激励所带来的背景噪声的影响，并分别在正常实验环境和背景噪声环境下，对A型叶片的第3阶阻尼进行测试，表10给出了两种环境下获得的第3阶阻尼结果及其标准差。

表10 有无背景噪声下A型叶片第3阶阻尼比及其标准差

根据表10测试结果可以看出，A型叶片在有背景噪声的环境下，其第3阶阻尼对应的标准差为4.29%，大于正常实验环境下的标准差值，因此可知复合材料叶片的阻尼会受到背景噪声的影响，且其阻尼不确定性的程度会随着背景噪声的增大而增大。

Clouds come together northeastward in summer, several-day rain is coming;clouds come together southeastward in winter, white snow is coming then.

综上所述，通过对复合材料叶片开展的阻尼测试实验可知，其阻尼确实存在着不确定性现象，且其不确定性的程度会受到激励幅度、边界条件、背景噪声的影响。为解决不确定性带来的阻尼参数辨识问题，本文提出了线性平均方法，将自由衰减信号中多个衰减时刻对应的阻尼结果的平均值，作为最终的某阶模态阻尼结果。该方法操作方便、原理简洁易懂，能够快速获取某1阶阻尼参数，并在一定程度上降低了背景噪声信号对测试结果的影响。

5 结语

本文基于时域衰减信号，通过包络线法获得了复合材料叶片在不同衰减时刻下的阻尼结果，研究发现复合材料叶片确实存在阻尼不确定性现象。

同时，对复合材料叶片阻尼不确定性的影响因素进行分析，研究发现：

（1）随着激励幅度的减小，复合材料叶片的阻尼不确定性的程度逐渐减小，其阻尼具有振幅依赖性这一非线性特征；

（2）随着边界条件约束能力变差，复合材料叶片在不同衰减时刻下阻尼比的标准差由3.83%降低到1.89%，其阻尼不确定性的程度逐渐减小；

（4）可以通过线性平均的方法来获得复合材料叶片某阶阻尼的最终结果，进而求取标准差来量化表征其阻尼的不确定性程度。

[1]HASELBACH F,NEWBY A,PARKER R.Concepts&technologies for the next generation of large civil aircraft engines[C].The 29 th congress of the international council of the aeronautical sciences,Petersburg,Russia,2014:1-10.

[2]傅恒志.未来航空发动机材料面临的挑战与发展趋向[J].航空材料学报，1998，18(4)：52-61.

[3]The behavior of structures composed of composite materials[M].Springer Science&Business Media,2006.

[4]齐红宇，温卫东，崔海涛.含孔复合材料层合板疲劳寿命预测研究[J].航空动力学报，2003，18(5)：658-661.

[5]KAW A K.Mechanics of composite materials[M].Boca Raton:The Chemical Rubber Company Press,2005.

[6]LEYENS C,KOCIAN F,HAUSMANN J,et al.Materials and design concepts for high performance compressor components[J].AerospaceScience and Technology,2003,7(3):201-210.

[7]张晓蕾，于开平.热环境下某飞行器振动特性分析与模型修正[J].噪声与振动控制，2013，33(5)：67-71.

[8]VINSON J R,SIERAKOWSKI R L.The behavior of structures composed of composite materials[M].Dordrecht,Netherlands:Springer Science and Business Media,2006.

[9]汤彬，孙志刚，高希光，等.单向陶瓷基复合材料阻尼计算方法[J].航空动力学报，2010，25(10)：2217-2222.

[10]张大义，洪杰，任德新.碳陶双基体复合材料壳结构的振动分析[J].航空动力学报，2011，26(5)：1142-1147.

[11]戴德沛.阻尼技术的工程应用[M].北京：清华大学出版社，1991：40-48.

[12]ABDERRAHIM EL MAHI,MUSTAPHA ASSARAR,YOUSSEF SEFRANI,etal.Dampinganalysisof orthotropic composite materials and laminates[J].Composites:Part B,39(2008):1069-1076.

[13]CRANE R M,GILLESPIE J W.Characterization of the vibration damping loss factor of glass and graphite fiber composites[J].Composites Science and Technology,1991,40(91):355-375.

[14]BERTHELOT J M,SEFRANI Y.Damping analysis of unidirectionalglassand Kevlarfibrecomposites[J].Composites Science and Technology,2004,64(9):1261-1278.

[15]BOTELHO E,CAMPOS A,DE BARROS E,et al.Damping behavior of continuous fiber/metal composite materials by the free vibration method[J].Composites Part B:Engineering,2006,37(2):255-263.

[16]SUM NAM JUNG,SEUNG JO KIM.Aeroelastic response of composite rotor blades considering transverse shear and structural damping[J].AIAA Journal,1994,32(4):820-827.

[17]KOSTOPOULOS V,KORONTZIS D T.A new method forthe determination ofviscoelastic properties of composite laminates:a mixed analytical–experimental approach[J].Composites Science and Technology,2003,63(10):1441-1452.

[18]李典森，卢子兴，李嘉禄，等.三维编织复合材料振动阻尼特性的实验研究[J].机械强度，2009，37(2)：211-214.

[19]杨强，邵闯，张治君.航空发动机复合材料叶片振动特性分析[J].结构强度研究，2013(2)：57-60.

[20]杨云昭，易凯，王建月，等.国产碳纤维增强树脂基复合材料阻尼性能实验研究[J].强度与环境，2014，41(6)：402-428.

[21]倪楠楠，温月芳.PDDF对芳纶无纺布/环氧树脂复合材料力学和阻尼性能的影响[J].复合材料学报，2015，32(6)：1791-1799.

Damping Uncertainty Test of Composite Blades Based on Time-domainAttenuation Signals

LIANG Xiao-long,LI Hui,NIU Yi,ZHOU Zheng-xue
(School of Mechanical Engineering&Automation,Northeastern University,Shenyang 110819,China)

The damping uncertainty of composite blades is tested and studied using time-domain attenuation signals.First of all,the damping test system for composite blades is set up,and the test procedure of damping uncertainty is designed so that the uncertainty level of a certain-order damping can be quantified by the index of standard deviation.Then,with three different types of TC500 carbon fiber/resin composite straight-panel blades as the objects,their damping results at different attenuation time are obtained by the testing.And the damping uncertainty phenomenon is confirmed.Finally,the influence rules of exciting levels,boundary conditions and background noise levels on the damping uncertainty of the composite blades are discussed.Consequently,linear average technique is proposed to accurately obtain the final damping results.

vibration and wave;time-domain attenuation signal;composite blade;damping;uncertainty test;influence factors analysis

TB535

A

10.3969/j.issn.1006-1355.2017.05.042

1006-1355(2017)05-0204-06+213

2017-04-21

梁晓龙（1989－），男，沈阳市人，硕士生，主要研究方向为复合材料振动测试研究。

E-mail:308361550@qq.com