悬臂黏弹性体夹层梁的非线性随机振动抑制性能分析

张 巍，应祖光，张四康

（1.浙江理工大学 经济管理学院实验中心，杭州 310018；2.浙江大学 航空航天学院力学系，杭州 310027）

悬臂黏弹性体夹层梁的非线性随机振动抑制性能分析

张 巍1，应祖光2，张四康2

（1.浙江理工大学 经济管理学院实验中心，杭州 310018；2.浙江大学 航空航天学院力学系，杭州 310027）

悬臂黏弹性夹层梁的随机振动抑制是一个重要的实际问题。采用性能可控黏弹性体的夹层梁具有无需改变结构设计的可优化性与对于较宽频带激励的适应性。关于两端约束可控黏弹性夹层梁的线性振动已有一定研究，而非线性振动仍有待于进一步讨论。悬臂黏弹性夹层梁高阶模态的求解是一个较为复杂的问题。高斯宽带随机激励下黏弹性夹层梁的非线性多模态耦合振动分析是一个较为困难的问题。考虑黏弹性体的物理非线性，首次建立悬臂黏弹性夹层梁的非线性运动微分方程，确定振动模态，根据伽辽金法将该方程离散化为多模态耦合的非线性振动方程；对于高斯平稳随机激励，运用统计线性化法推导等价拟线性系统，计算系统的随机响应，得到悬臂黏弹性夹层梁非线性随机振动的均方位移，及等价的频响函数和功率谱；通过数值分析结果说明，悬臂黏弹性夹层梁对非线性随机振动具有有效的抑制性能。

振动与波；随机振动；悬臂梁；非线性黏弹性体；高斯平稳激励；均方根响应

悬臂梁是工程结构中一类重要的支承构件，它在约束端支座激励下容易产生较大幅度的振动，而不确定环境常常导致支座的随机运动激励，因此悬臂梁的非线性随机振动抑制是重要的实际问题。由于减振器安装限制，采用黏弹性材料构造复合悬臂梁成为振动控制的一个有效措施。关于不可控阻尼夹层梁的振动抑制已有很多研究[1–3]，但其控制效果受环境（例如激励频率）改变而退化。近年来发展了一种性能可控的黏弹性体[4]，其动力学特性（例如刚度与损耗因子）可通过外加磁场调节。该可控黏弹性体已用于构造复合梁以抑制振动，该复合梁具有无需改变结构设计的可优化性、及对于较宽频带激励的适应性等优点。关于两端约束的可控黏弹性夹层梁的频响特性、周期振动响应、随机振动响应等已有一定研究[5–9]，文献[10]研究了悬臂黏弹性夹层梁的随机微振动响应，但所用的动力学模型在几何和物理上都是线性的。然而，随着激励增强，复合梁特别是悬臂梁的振动变形将相应地增大，其中黏弹性体首先表现出物理非线性[11]。因此，较强激励下悬臂黏弹性夹层梁的振动需要考虑非线性因素。

高斯随机激励是较为普遍的环境载荷，这类宽频带随机激励将导致梁包含低阶到高阶的多模态耦合振动，因此高斯随机激励下悬臂黏弹性夹层梁的振动需要考虑多个模态，进行耦合振动分析。然而，高自由度非线性系统的随机振动分析仍是目前一个复杂而困难的问题。对于黏弹性夹层梁的非线性随机外激振动，统计线性化法是目前一个主要而有效的分析方法[12]。此外，伽辽金法是目前将连续体梁离散化为多自由度系统的一个主要而有效的分析方法，但悬臂梁高阶模态的求解比简支梁复杂得多，这极大地增加了伽辽金法应用的难度，因此悬臂梁的高模态耦合非线性随机振动研究相对很少。然而，非线性随机振动响应的分析解是检验数值计算结果可靠性与评估黏弹性夹层梁振动抑制效果的依据。

本文考虑可控黏弹性体的物理非线性，研究该悬臂黏弹性夹层梁在随机支座运动激励下的多模态耦合非线性随机振动响应。先基于黏弹性体的非线性本构关系，按照复合结构理论，建立黏弹性夹层梁关于纵横位移的非线性耦合运动微分方程，确定一端约束与另一端自由的边界条件；再根据伽辽金法将该偏微分方程组转化为常微分方程组，得到关于梁横向位移的多自由度非线性振动方程，及边界约束方程；然后根据随机振动理论，运用统计线性化法推导等价拟线性系统，计算系统的随机响应，得到悬臂黏弹性夹层梁非线性随机振动的均方位移，同时得到等价的频响函数和功率谱；最后给出数值结果，阐明该悬臂黏弹性夹层梁的非线性随机振动抑制性能。

1 悬臂非线性黏弹性夹层梁的方程

考虑悬臂黏弹性夹层梁，它在实际问题中有横、斜、竖等姿态，重力对于振动的影响较小而略去。这里以竖立的悬臂黏弹性夹层梁为例，其结构简图如图1所示。

图1 悬臂黏弹性夹层梁

梁长为L，左右两层是弹性材料，其厚度、弹性模量、密度分别为h1、E1、ρ1，中间层是黏弹性材料，其厚度、密度分别为h2、ρ2，其弹性模量比弹性层小得多故不计，剪切模量为G2。夹层梁受随机支座运动(水平位移w0)激励，设为高斯平稳过程。对于较强振动，考虑黏弹性体的物理非线性，其切应力τ2是切应变γ2及其导数的非线性函数，表示为[11]

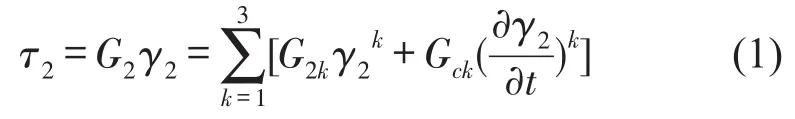
式中G2k和Gck是常数，t是时间。

基于多层复合结构理论与梁的基本假设，由变形几何关系得到夹层梁的左、右边层中任意点的纵向(z轴方向)位移u1与u3分别为[1–3]

式中u10与u30分别是左右层的中性层的纵向位移，w是梁的横向(x轴方向)位移，x与z坐标如图1所示。对位移式(2)求导可得相应层中各点的纵向正应变，再由物理关系得到正应力为

由单元体z方向的平衡得到左右边层中相应点的切应力为

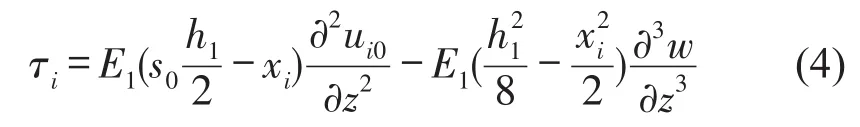
式中i=1,3，当i=1时s0=1，当i=3时s0=-1。设中间黏弹性层的横截面始终保持平面，利用式(2)计算其切应变，再由式(1)得到相应切应力为

式中ha=h1+h2。梁纵向惯性相对较小故不计。根据夹层梁各层界面间切应力的连续性，得到关于纵向位移的微分方程

式中u=u10=-u30。再由夹层梁单元x方向的动平衡得到关于横向位移的运动微分方程

式中ρht=2ρ1h1+ρ2h2。式(6)和(7)组成悬臂黏弹性夹层竖梁关于纵横位移的非线性耦合运动微分方程。该悬臂梁的边界条件为一端约束、另一端自由，约束端(z=0)的横向位移、角位移及纵向位移分别为

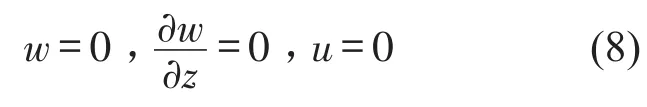
自由端(z=L)弯矩、轴向力及剪力为零分别导致

边界条件式(8)与式(9)表明悬臂梁的振动模态比简支梁复杂得多。由式(6)和式(7)的自由振动方程与边界条件式(8)和式(9)确定振动模态，对于纵向位移为正弦函数，对于横向位移为谐波函数与指数函数的组合。利用该振动模态展开悬臂梁的纵向与横向振动位移，无量纲化的级数形式为

式中n是整数，y=z/L是无量纲坐标，wa是无量纲位移，wa是支座位移幅值，pi、qi是时间的函数，φi、φi是模态函数，λij(j=1，2，3，4)是常数，由边界条件确定。按照伽辽金法，将式(10)代入式(6)和式(7)，利用模态正交性简化，得到关于pi与qi的方程组，再略去高阶小量，消去pi得到关于qi的常微分方程组，表示成矩阵形式为

式中Q=[q1，q2，…，qn]T，M、C、K分别是广义质量、阻尼和刚度矩阵，CN、KN分别是非线性阻尼和刚度矩阵，F是广义激励向量，由支座运动w0确定。方程(12)描述了悬臂黏弹性夹层梁在支座运动激励下的非线性多模态耦合振动，或非线性多自由度系统受随机外激的耦合振动。

2 基于统计线性化的随机振动响应

悬臂黏弹性夹层梁在随机支座运动激励下的振动为随机过程。方程(12)表明多自由度非线性系统式(12)承受随机外部激励，运用统计线性化法可有效地估计系统响应[12]。按照该方法，设非线性系统式(12)的等价拟线性系统为

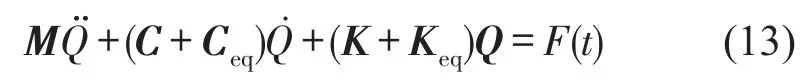
式中Ceq、Keq分别是等价线性阻尼与刚度矩阵。方程式(12)与式(13)左边之差为

由其均方极小，即E[ΔTΔ]→min，得到关于Ceq与Keq的代数方程组为

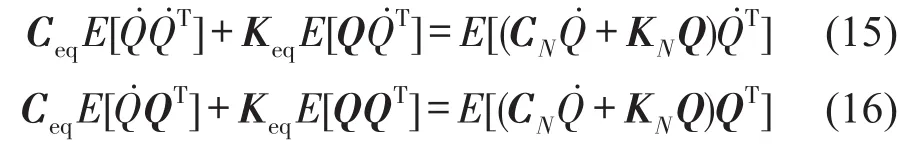
式中E[·]是期望算子。由式(15)和式(16)解得等价线性阻尼与刚度，代入式(13)即确定了等价拟线性系统。对于高斯随机激励，线性系统的响应是高斯过程，则等价线性阻尼和刚度依赖于系统式(13)的均方响应。等价线性系统式(13)的频响函数与响应功率谱密度矩阵分别为

式中ω是振动频率，SF是激励功率谱，j是虚数单位，*表示复共轭。利用式(17)与式(18)，由式(10)可计算悬臂黏弹性夹层梁的等价频响函数与响应功率谱密度，从而进一步计算夹层梁响应统计量，例如无量纲均方位移为

许多环境激励可模拟为滤波高斯白噪声，即由高斯白噪声通过线性微分系统生成。考虑悬臂黏弹性夹层梁承受该随机支座运动激励(无量纲水平位移其平稳功率谱为

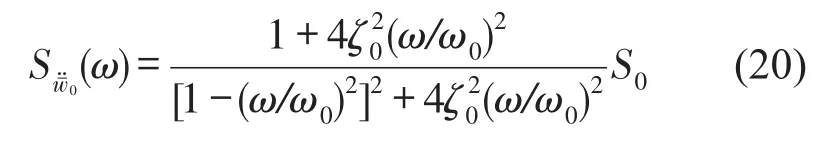
式中ω0、ζ0是常数，S0是激励强度参数。上述悬臂黏弹性夹层梁在支座运动激励下非线性随机振动响应的计算过程如下：首先由式(11)、式(8)和式(9)计算系数λij，确定振动模态；然后选取均方响应初值，由式(15)和式(16)求解等价阻尼与刚度，再由式(17)和式(18)计算等价频响函数与功率谱密度，计算均方响应；检查收敛性，迭代直至达到指定精度，最后计算得到夹层梁的均方位移式(19)。

3 数值结果

考虑悬臂黏弹性夹层梁及随机激励具有基本参数：L=4 m，h1=5 cm，h2=20 cm，ρ1=3 000 kg/m3，ρ2=1 200 kg/m3，E1=10 GPa，G21=2.0 MPa，G22=0.2G21，G23=0.02G21，Gc1=0.2 MPa·s，Gc2=0.2Gc1，Gc3=0.02Gc1，S0=1.0，ω0=23 rad/s，ζ0=0.3，wa=1，y=1。按照上述方法计算梁自由端响应，数值结果如图2－图5所示。图2展示了有与无黏弹性夹层梁自由端的无量纲均方根横向位移响应随无量纲随机支座水平运动激励强度(S0)的变化，其中点线为无中间黏弹性层情形的响应，实线为有中间黏弹性层情形的响应，离散点为数值模拟结果。

图2 有与无黏弹性夹层梁的均方根位移随激励强度变化

可见数值模拟方法验证了本文的分析方法，与无夹层梁相比，黏弹性夹层梁能够大大降低支座运动激励产生的非线性随机振动响应。

图3 线性与非线性黏弹性夹层梁的均方根位移随激励强度变化

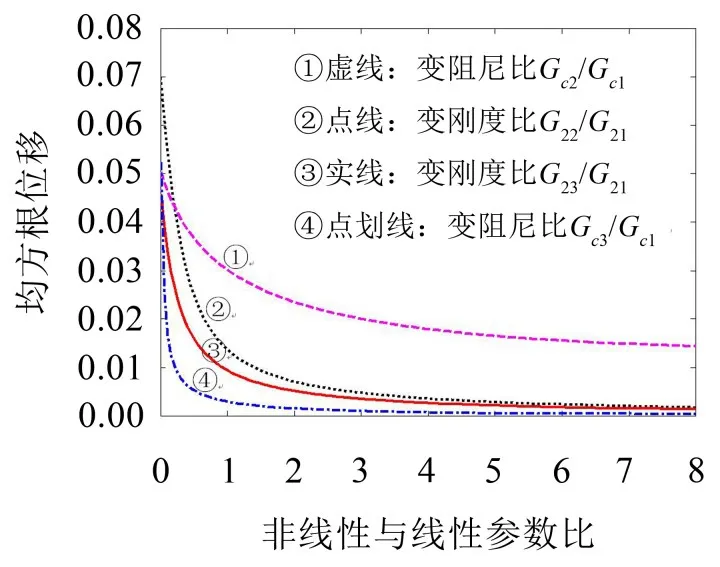
图4 黏弹性夹层梁的均方根位移随非线性与线性参数比值变化

因此对于一定范围内性能可控的黏弹性材料(例如阻尼与刚度可由外部磁场调节)，其夹层梁无需改变结构设计，仅通过性能控制即可实现非线性随机振动响应降低的优化。

图5展示了不同黏弹性层厚度夹层梁自由端的无量纲均方根横向位移响应随无量纲随机支座水平运动激励强度(S0)的变化，其中点线为黏弹性层厚度h2=20 cm时的响应，实线为黏弹性层厚度h2=30 cm时的响应，虚线为黏弹性层厚度h2=40 cm时的响应。可见夹层梁的非线性随机振动响应随黏弹性层厚度的增加而减小。

对于软非线性刚度与阻尼G22=-0.2G21，G23=-0.02G21，Gc2=-0.2Gc1，Gc3=-0.02Gc1(其余参数不变)，图6展示了黏弹性夹层梁自由端的无量纲均方根横向位移响应随无量纲随机支座水平运动激励强度(S0)的变化，其中点线为线性黏弹性(G23=G22=0，Gc3=Gc2=0)时的响应，实线为非线性黏弹性时的响应，离散点为数值模拟结果。

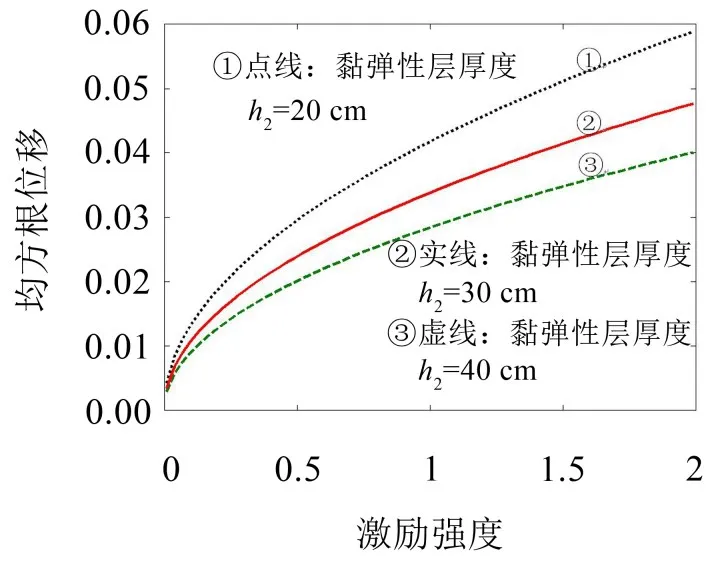
图5 不同黏弹性层厚度夹层梁的均方根位移随激励强度变化

图6 线性与软非线性黏弹性夹层梁的均方根位移随激励强度变化

可见软非线性刚度(G22，G23＜0)与阻尼(Gc2，Gc3＜0)导致黏弹性夹层梁的非线性随机振动响应稍高于线性振动响应，但黏弹性夹层梁的振动响应仍低于无黏弹性夹层梁的结果。

可见夹层梁的非线性随机振动响应总体上随非线性刚度或非线性阻尼减小而减小。对于一定的小非线性负阻尼Gc2，夹层梁的非线性随机振动响应有一个峰值，减振设计时需要避免。

总之，黏弹性夹层设计可用于悬臂梁等结构受基础激励的非线性随机振动抑制，性能可控的黏弹性材料为该夹层结构振动控制提供了不改变结构设计的可优化性、及对于较宽频带环境激励的适应性。

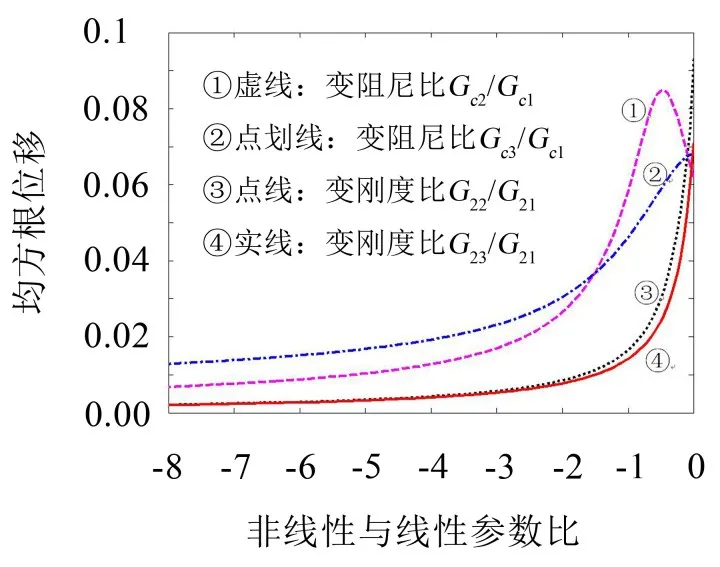
图7 软非线性黏弹性夹层梁的均方根位移随非线性与线性参数比值变化

4 结语

本文研究了悬臂黏弹性夹层梁在支座运动激励下的非线性随机振动响应。考虑黏弹性层的物理非线性，建立了悬臂黏弹性夹层梁关于纵横位移的非线性耦合运动微分方程，利用边界条件确定振动模态，根据伽辽金法导出关于梁横向模态位移的多自由度非线性振动方程。对于高斯随机环境激励，运用统计线性化法推导出了等价拟线性系统，计算系统的随机响应，得到了悬臂黏弹性夹层梁非线性随机振动的均方位移、及等价频响函数和功率谱等。数值结果说明了悬臂可控黏弹性夹层梁的非线性随机响应特性，有效的振动抑制性能，及硬软非线性的影响规律。增加黏弹性层厚度可降低夹层梁的非线性随机振动响应，且响应降低的幅值随激励强度而增加；提高黏弹性层非线性刚度、非线性阻尼的比例(相对线性部分)也可降低夹层梁的非线性随机振动响应，但在该比值较小时影响更加显著；而软非线性阻尼比例对于夹层梁非线性随机振动响应的影响并非单调，需要避免响应峰值情形。

[1]DITARANTO R A.Theory of the vibratory bending for elastic and viscoelastic layered finite-length beams[J].ASME Journal of Applied Mechanics,1965(32):881-886.

[2]MEAD D J,MARKUS S.The forced vibration of a threelayer,damped sandwich beam with arbitrary boundary conditions[J].Journal of Sound and Vibration,1969(10):163-175.

[3]YAN M J,DOWELL E H.Governing equations for vibrating constrained-layer damping sandwich plates and beams[J].ASME Journal of Applied Mechanics,1972(94):1041-1046.

[4]CARLSON J D,JOLLY M R.MR fluid,foam and elastomer devices[J].Mechatronics,2000(10):555-569.

[5]ZHOU G Y,WANG Q.Study on the adjustable rigidity of magnetorheological-elastomer-based sandwich beams[J].Smart Materials and Structures,2006(15):59-74.

[6]CHOI W J,XIONG Y P,SHENOI R A.Vibration characteristics of sandwich beam with steel skins and magnetorheologicalelastomercores[J].Advances in Structural Engineering,2010(13):837-847.

[7]NAYAK B,DWIVEDY S K,MURTHY KSRK.Dynamic analysis of magnetorheological elastomer-based sandwich beam with conductive skins under various boundary conditions[J].Journal of Sound and Vibration,2011(330):1837-1859.

[8]张四康，应祖光.高斯激励黏弹性夹层梁的非线性随机响应特性[J].噪声与振动控制，2017，37(1)：1-4.

[9]张巍，应曌中，应祖光.MRVE夹层梁随机振动的最优跳变参数控制[J].噪声与振动控制，2015，35(4)：121-123.

[10]YING Z G,NI Y Q.Micro-vibration response of a stochastically excited sandwich beam with a magnetorheological elastomer core and mass[J].Smart Materials and Structures,2009(18):095005.

[11]YING Z G,NI Y Q,SAJJADI M.Nonlinear dynamic characteristics of magneto-rheological visco-elastomers[J].Science China,Technological Sciences,2013(56):878-883.

[12]ROBERTS J B,SPANOS P D.Random vibration and statistical linearization[M].Chichester:John Wiley&Sons,1990.

Nonlinear Random Vibration SuppressionAnalysis of Viscoelastic Sandwich Cantilever Beams

ZHANG Wei1,YING Zu-guang2,ZHANG Si-kang2
(1.Laboratory Center,School of Economics and Management,Zhejiang Sci-Tech University,Hangzhou 310018,China;2.Department of Mechanics,School ofAeronautics andAstronautics,Zhejiang University,Hangzhou 310027,China)

Random vibration suppression of viscoelastic sandwich cantilever beams is an important subject in engineering.The sandwich beam with a controllable viscoelastic core can be optimized without structural change and has the suitability to wide-band excitation.The linear vibration of the controllable viscoelastic sandwich beams with both ends constrained has been studied.However,their nonlinear vibration needs to be studied further.The solution for high-order modes of the viscoelastic sandwich cantilever beams is a complicated problem.And the nonlinear multi-mode-coupling vibration analysis of the viscoelastic sandwich beams under Gaussian wide-band random excitation is a challenging problem.In this paper,the nonlinear viscoelastic constitutive relation is considered.The differential equations of motion of a viscoelastic sandwich cantilever beam under support excitations are derived.The vibration modes of the cantilever beam are determined by the constraint conditions at both ends.The partial differential equations are converted into nonlinear multimode-coupling vibration equations by using the Galerkin method.The equivalent quasi-linear system is derived for the Gaussian stationary random excitation by using the statistic linearization method.The random responses such as MS displacement,equivalent frequency response and power spectral density of the nonlinear random vibration of the cantilever beam are obtained.Numerical results illustrate the good suppression effectiveness of the nonlinear random vibration of the viscoelastic sandwich cantilever beams.

vibration and wave;random vibration;cantilever beam;nonlinear viscoelasticity;Gaussian stationary excitation;RMS response

O324；O328

A

10.3969/j.issn.1006-1355.2017.05.004

1006-1355(2017)05-0018-05+49

2017-02-14

国家自然科学基金资助项目（11572279）；浙江省自然科学基金资助项目（LY15A020001）

张巍（1965－），女，江苏省南通市人，高级工程师，主要从事信息系统与控制研究。

E-mail:zhweihz@zstu.edu.cn