适用于MEMS振动陀螺仪的相位读出自校准方法*

许建军，王玮冰，李 佳

(1. 中国科学院微电子研究所，北京 100020； 2. 中国科学院物联网研究发展中心，江苏 无锡 214000；3. 中国科学院大学，北京 100049； 4. 昆山光微电子有限公司，江苏 苏州 215300)

适用于MEMS振动陀螺仪的相位读出自校准方法*

许建军1,2,3，王玮冰1,4，李 佳1

(1. 中国科学院微电子研究所，北京 100020； 2. 中国科学院物联网研究发展中心，江苏 无锡 214000；3. 中国科学院大学，北京 100049； 4. 昆山光微电子有限公司，江苏 苏州 215300)

相比于传统陀螺仪，MEMS振动陀螺仪具有体积小、质量轻、功耗低、价格低廉等优势，但是由于其本身结构的局限性和工艺加工水平的限制，其在性能上还处于低精度陀螺仪的行列。目前已有若干MEMS自校准方案可以应用于MEMS振动陀螺仪以提高其精度指标，然而已有的技术存在着只能消除某一种因素对精度的影响、需要高精度转台系统支撑或者校准的灵敏度不高等不足。为解决上述问题，设计并提出了一种基于相位读出的MEMS振动陀螺仪自校准方案，该方案能消除工艺误差、器件老化、外部环境变化对陀螺仪精度的影响，而且该方案不需要高精度转台系统支撑、能够消除绝大部分因素对精度的影响、校准的灵敏度更高。实验仿真结果表明，该方案能实现MEMS振动陀螺仪的自校准，提高测量精度，扩大MEMS振动陀螺仪的适用范围。

微机械振动陀螺仪；自校准；精度；电信号

0 引言

微电子机械系统(Micro Electro-Mechanical System, MEMS)是在集成电路工艺的基础上发展起来。MEMS陀螺仪是利用微机械加工技术制作的能够检测旋转角速度的惯性传感器。MEMS陀螺仪具有体积小、质量轻、功耗低、抗过载能力强、价格低廉等优点[1]。由于MEMS陀螺仪的本身的局限性和工艺加工水平的限制，现阶段开发的MEMS陀螺仪易受外部环境变化、器件结构老化、电学特性改变、加工工艺等因素的影响，MEMS陀螺仪的精度一直较低，限制了MEMS陀螺仪的应用范围。

1 研究背景

1.1MEMS陀螺仪传统标定校准

MEMS陀螺仪中包含电学、机械模块，结构复杂；陀螺仪的测量精度容易受到外部环境及陀螺仪自身参数的影响。所以要对MEMS陀螺仪进行校准需要考虑的因素很多，实现的难度较大。传统陀螺仪的标定校准主要依靠高精度转台系统测量出不同旋转角速度下陀螺仪的输出大小，绘制输入和输出的关系图，通过直线拟合的方法得到校准后的标度因数和零漂，从而实现陀螺仪的标定校准。但是传统陀螺仪的标定校准需要高精度转台以及其他外部设备做支撑，操作相对复杂，成本较高；而且只进行一次出厂校准，环境因素、器件老化、温度变化等因素还是会在陀螺仪运行过程中影响陀螺仪的精度。

1.2MEMS陀螺仪已有自校准方法

为了提高陀螺仪的精度，国外相关研究团队开发出了多种校准技术。例如，能够补偿陀螺仪系统中电阻、电容、谐振频率对摆幅测量造成误差的边频带检测技术[2]，基于频率的温度补偿技术[3]，用于补偿驱动力不重合误差的双斜坡融合技术[4]等。以上几种方案都能不同程度地改善陀螺仪的精度。但是这些方案都是消除或减弱了某一种因素对精度的影响，都是针对不同的影响因素提出的局部解决方案。2012年佐治亚理工学院的研究团队针对MEMS振动陀螺仪开发出的自校准方案[5]能够实现零漂和标度因素的同时校准。该方案验证了可以采用电激励信号代替高精度转台实现陀螺仪的自校准。但该方案在校准模态下得到的标度因素较小，测量的灵敏度不高。

基于以上因素本文设计出适用于MEMS振动陀螺仪的自校准方案。本方案采用新的输入电信号作用于陀螺仪模型，结合相应信号处理电路能够实现对陀螺仪零漂和标度因素的校准，摆脱了校准对高精度转台的依赖，降低校准成本，同时输出的结果容易测量、灵敏度也更高。

2 相位读出自校准方案

传统标定校准根据检测模态下陀螺仪的摆幅来测量旋转角速度的大小。与传统标定校准不同，自校准方法是在校准模态下根据陀螺仪位移信息中的相位偏移量的大小来测量旋转角速度。

本文设计的相位读出自校准方案主要包括陀螺仪的两个振动模态：校准模态和检测模态。校准模态下通过设计合适的电激励信号模拟高精度转台作用于陀螺仪模型，设计合适的信号处理电路从陀螺仪输出信号中提取出相移分量作为系统的输出，使系统最后输出的电压信号能直接反应旋转角速度的大小，从而得到不同旋转角速度下陀螺仪的输出信号，实现陀螺仪的自校准。在检测模态下可以根据系统输出电压和系统输入与输出之间的关系计算出此时的旋转角速度。

2.1校准模态

本文将MEMS振动陀螺仪等效为两自由度弹簧——质量块模型[5]，陀螺仪校准模态下的动力学方程如式(1)。在校准模态时将陀螺仪固定不动，用正弦驱动信号Fcos(wt)和Fsin(wt)作用于陀螺仪，再外加一个电激励信号cos(Ωt)模拟转台的旋转，将驱动信号和电激励信号经过乘法器、异相器和加法器之后得到Fcos(w+Ω)t和Fsin(w+Ω)t作为陀螺仪系统的输入，如图1所示。

图1 基于相位读出自校准方案的信号产生电路图

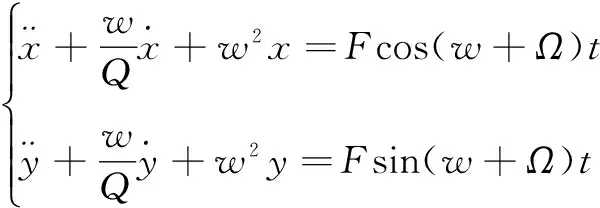
(1)

陀螺仪模型输出的电流信号x(t)、y(t)。w是正弦电激励信号的频率，Q是陀螺仪的品质因数，λ[6]是与陀螺仪类型相关的常量，λ的关系式为λ=2n/n2+1，n为陀螺仪包含的简并谐振模式对的个数。Ω为旋转角速度，F是常量。解上述方程可得到陀螺仪输出端的电流信号：

(2)

其中，相移θ3为：

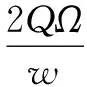
(3)

图2为基于相位读出方案整体系统框图，包含输入信号产生部分、MEMS陀螺仪模型、放大电路、解调电路和低通滤波器电路。

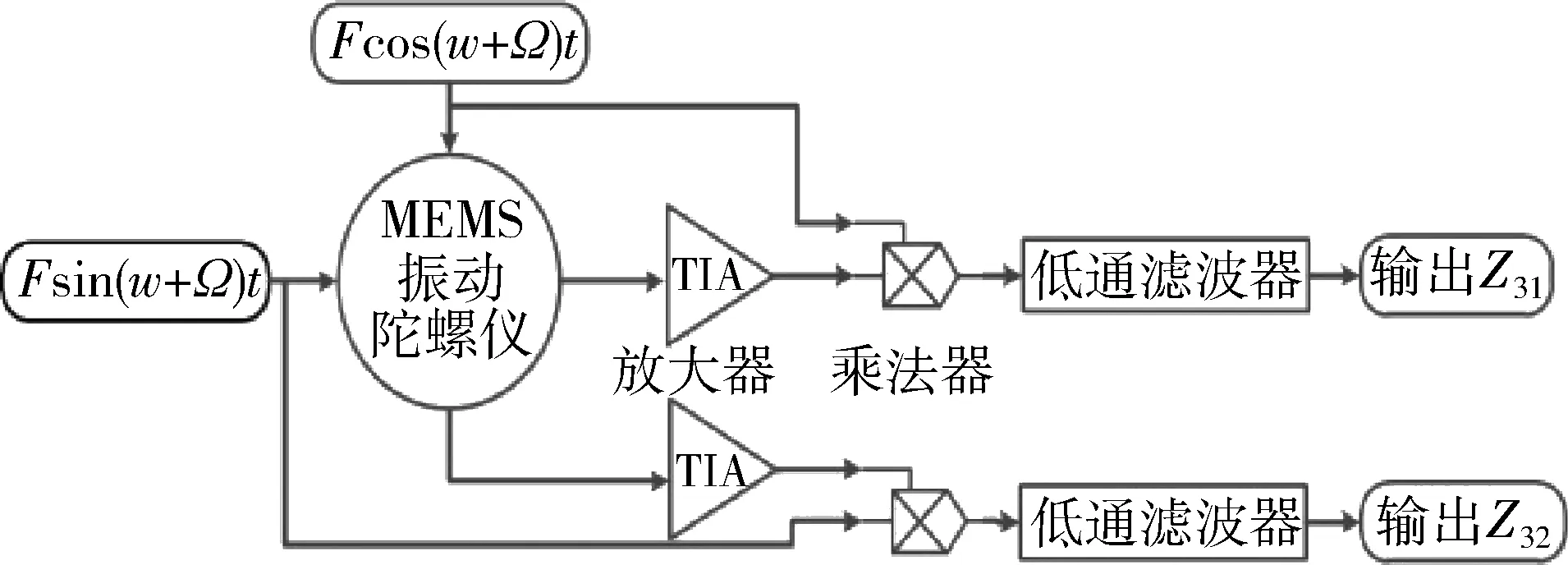
图2 相位读出方案下校准模态的系统框图

将陀螺仪的输出信号放大后分别与Fcos(w+Ω)t、Fsin(w+Ω)t相乘进行解调，然后再经过低通滤波器，得到最后输出直流电压如式(4)，在Ω×Q远小于w的情况下，输出电压的大小与角速度信号Ω近似成线性关系。

(4)

2.2检测模态

检测模态时陀螺仪用于测量所处环境的旋转角速度，这里陀螺仪所处的环境就是高精度转台上，系统的输入是驱动信号Fcos(wt)、Fsin(wt)和高精度转台的旋转角速度Ω。此时陀螺仪工作在检测模态，图3为检测模态系统模型图，则此时MEMS陀螺仪两自由度弹簧-质量块模型的微分方程组如式(5)。

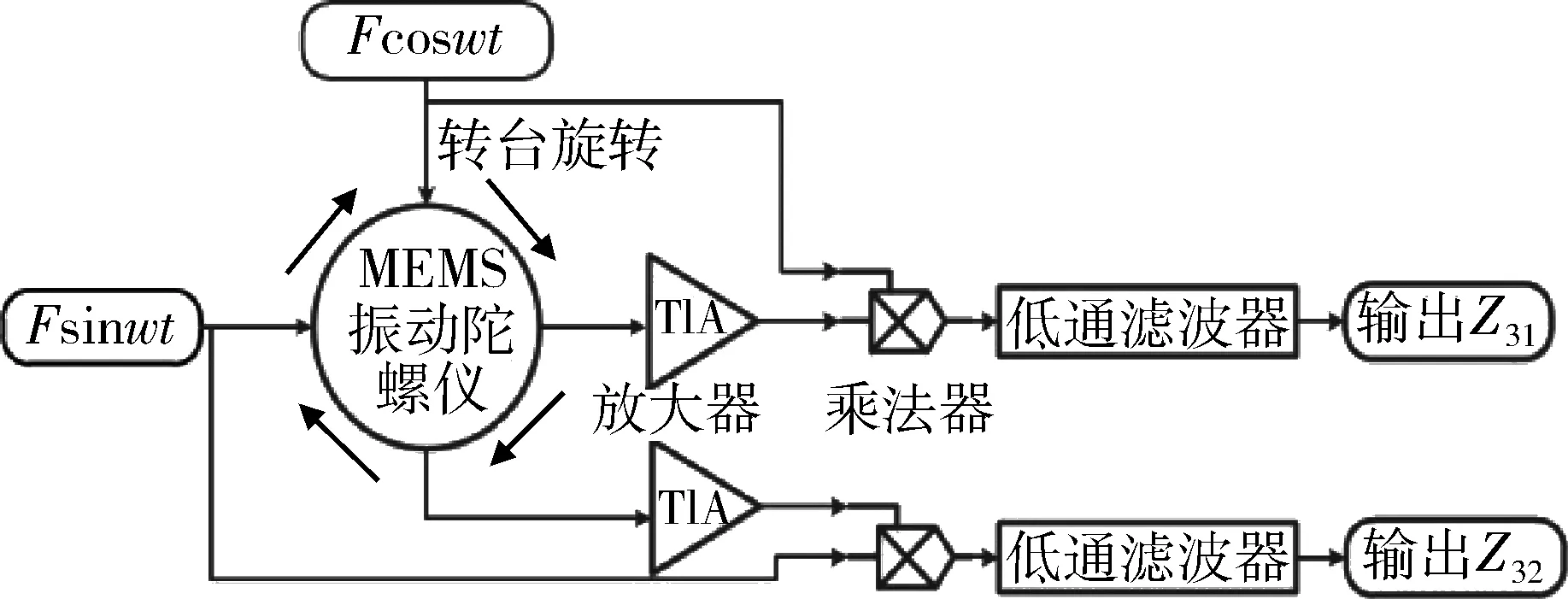
图3 基于相位读出方案的检测模态系统框图

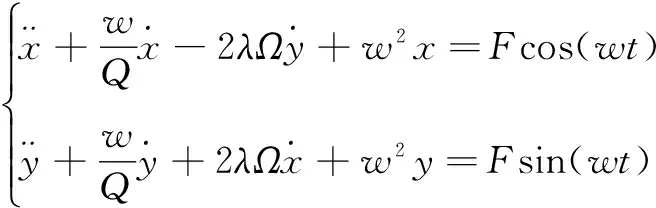
(5)

解检测模态下陀螺仪的微分方程组可得：

(6)

其中相移θ1为：

(7)

陀螺仪的输出电流信号分别是x(t)、y(t)，先后经过跨阻放大器和电压放大器，然后分别与Fcos(wt)、Fsin(wt)相乘进行解调得到W(t)，如式(8)。

(8)

解调后的信号再通过二阶低通滤波器将信号中的高频部分滤出，得到最后输出直流信号如式(9)，由此式可知在Ω×Q远小于w时，输出电压与转台旋转角速度近似成线性关系。

(9)

对比陀螺仪处于检测模态和校准模态下输出端的信号，发现陀螺仪输出信号都产生了一个相移，相移θ1和θ3只相差一个与陀螺仪运动模态相关的常数λ，而且系统最后的输出只与相移信号有关。因此本方案的电激励信号都可以用来代替高精度转台实现陀螺仪的自校准。

3 结果测试分析

为了验证上文的公式推导，本文选用MEMS振动盘振动陀螺仪为研究对象，仿真采用的驱动信号的摆幅F=2 V，驱动信号频率f=10 MHz，电激励信号频率变化范围为0～10 Hz，MEMS振动盘振动陀螺仪的品质因数Q=20 000[5]。根据自校准方案的输入电信号以及解调信号，设计相应的硬件电路，并进行测试仿真。由于陀螺仪在校准模态下I和Q两个简并谐振模式相互独立、互不影响，而两个微分方程基本一致，仿真结果也佐证了上述结论，因此下面只列出了I简并模式下的仿真结果。

3.1校准模态测试分析

校准模态下，用信号发生器产生系统的驱动信号和电激励信号，通过信号产生电路作用于MEMS陀螺仪。

图4是本方案的信号处理电路，将参数带入式(2)得陀螺仪输出端的电流信号为30 uAsin[(w+Ω)t-θ3]，可以用电流源模拟陀螺仪的输出电流。之后通过一个跨阻放大器将电流信号放大为0.3 mV的电压信号，然后通过一个20/3倍的运算放大器将信号摆幅放大到2 V，再与信号源提供的解调信号2cos(w+Ω)t进行解调，最后通过电阻和电容组成的二阶低通滤波器，得到最终的输出。

图4 基于相位读出自校准方案的信号处理电路

调节校准模态下电激励信号的角速度从0～10 Hz变化，选取不同角速度对电路进行仿真，记录不同角速度下输出电压值，得到最后的电压-旋转角速度关系图如图5。根据仿真数据进行最小二乘法拟合，得到相位读出自校准方案的电压-角速度的直线关系为y=7.28x-0.37 mV，线性相关度为0.999 7。

图5 基于相位读出方案下电压-旋转角速度关系图

3.2检测模态测试分析

检测模态下将载有MEMS振动盘陀螺仪的PCB电路板固定在高精度转台上，通过不断改变高精度转台的旋转角速度，绘制出陀螺仪输入角速度与输出电压之间的关系图，陀螺仪的输出经过信号处理电路得到系统输出，用示波器对系统输出进行检测。

不断改变高精度转台的旋转角速度由0～10 Hz，并记录不同频率下对应的输出电压的变化。图6是高精度转台旋转角速度由0～10 Hz变化时对应的输出电压的变化图。将仿真数据经过直线拟合得到陀螺仪系统的标度因数约为4.79 mV/Hz。

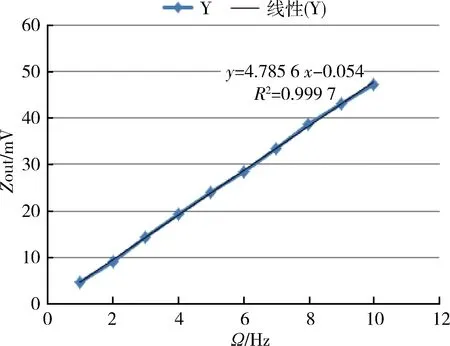
图6 高精度转台上系统输出与旋转角速度的关系

3.3原有方案校准模态测试分析

本文同时在相同输入信号摆幅和信号处理电路的基础上对已有方案的校准模态进行仿真，得到校准模态下的输出电压与旋转角速度的关系如图7，经过数据拟合得到已有方案校准模态下的标度因数为3.4。

图7 原有方案校准模态下的电压-角速度关系图

对比原有方案和相位读出方案的校准模态下的测试仿真得到，相位读出方案校准模态下测得标度因数大约是原有方案的两倍，即在相同的旋转角速度变化范围内，相位读出自校准方案输出电压变化更大，测量的结果更灵敏。

对比相位读出自校准方案检测模态和校准模态的测试仿真得到，检测模态下的标度因素为4.79，而校准模态下的标度因素为7.28，检测和校准模态下标度因数的不同是由于检测模态下谐振模式间存在耦合，最后输出包含耦合系数λ，校准模态下谐振模式不存在耦合，系统输出也不包含耦合系数，同时检测模态下陀螺仪谐振模态间还存在着频率偏差。因此在校准模态下得到系统的标度因数后需要乘以一个比例因数转化为检测模态下的标度因数，本方案测得比例因数为0.658。

4 结论

本文针对MEMS陀螺仪精度不高，而且校准需要高精度转台系统，操作复杂，成本高的问题，以MEMS振动盘陀螺仪为研究对象，提出了适用于MEMS振动陀螺仪的基于相位读出的自校准方案，理论推导和实验仿真都验证了该方案的可行性。采用相位读出自校准方案测得检测模态和校准模态下的标度因素分别为4.79和7.28，两者之间存在一个大小为0.658的比例因数。本文同时在相同条件下对原有调幅自校准方案校准模态进行测试仿真，测得标度因数为3.48。即新方案校准模态的标度因素为原有调幅自校准方案的两倍，即在相同的旋转角速度变化范围内，相位读出自校准方案测得输出电压变化更大，测量的标度因数更灵敏。

[1] VIGNA B. It makes sense: how extreme analog and sensing will change the world[J]. in Tech. Digest 2012 Solid-State Sensors, Actuators and Microsystems Workshop, Hilton Head, SC, June 2012: 58-65.

[2] TRUSOV A A, SHKEL A M. A novel capacitive detection scheme with inherent self-calibration[J]. IEEE/ASME Journal of Microelectromechanical Systems, 2007,16(6): 1324-1333.

[3] PRIKHODKO I P, TRUSOV A A, SHKEL A M. Compensation of drifts in high-Q MEMS gyroscopes using temperature selfsensing[J]. Sensors and Actuators A Physical, 2013, 201(5): 517-524.

[4] PRIKHODKO I P, MERRITT C, GKEGORY J A, et al. Continuous self-calibration canceling drive-induced errors in MEMS vibratory gyroscopes[J]. Transducers, June 2015:35-38.

[5] CASINOVI G, SUNG W K, DALAL M, et al. Electrostatic self-calibration of vibratory gyroscopes[J]. in Proc. 25th IEEE Int. Conference on Micro Electro Mechanical Systems,Paris, France, Jan. 2012: 559-562.

[6] GALLACHER B J, BURDESS J S, HARRIS A J. Principles of a three-axis vibrating gyroscope[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(4): 1333-1343.

Phase readout self-calibration method of MEMS vibratory gyroscopes

Xu Jianjun1,2,3, Wang Weibing1,4, Li Jia1

(1. Institute of Microelectronics of Chinese Academy of Sciences, Beijing 100020, China;2. Chinese Academy of Sciences R&D Center for Internet of Things, Wuxi 214000, China;3. University of Chinese Academy of Sciences, Beijing 100049, China;4. Kunshan Optical Electronics Company, Suzhou 215300, China)

MEMS vibration gyroscope has the advantages of small size,light weight,low power consumption and low price. But because of the limitation of its structure and the limitation of the processing level, it is still in the ranks of low precision gyroscope. At present,several MEMS self-calibration schemes can be applied to MEMS vibration gyroscopes to improve their accuracy index.However,the existing technologies can only eliminate the influence of certain factor on the precise,or need high-precision turntable system,or not have a high precision. To overcome these problems,this paper designs and proposes a new self-calibration of fabricationerror,device burn-in and environment change to gyroscope’s precision.And the scheme does not need high-precision turntable system ,can eliminate the influence of most of factors and has high enough precision. The simulation result shows that this method can really realize self-calibration, improve the precision of gyroscopes and will make MEMS vibration gyroscopes be more extensively used.

MEMS vibratory gyroscopes; self-calibration; precision; electrical signal

TP212.1

A

10.19358/j.issn.1674- 7720.2017.19.012

许建军，王玮冰，李佳.适用于MEMS振动陀螺仪的相位读出自校准方法[J].微型机与应用，2017,36(19)：41-44.

国家自然科学基金面上项目(61370044); 国家863计划项目(2015AA042605)；国际合作专项经费，中科院-北大率先合作团队资助项目(201510280052，XMXX201200019933)；中国科学院科技服务网络计划(STS计划)项目

2017-04-11)

许建军(1989-)，通信作者，男，硕士研究生，主要研究方向：MEMS传感器自测试自校准等。E-mail：1215608223@qq.com。王玮冰(1977-)，男，博士，研究员，硕士生导师，主要研究方向：MEMS系统的混合信号读出电路以及新型高速模数转换器。李佳(1982-)，女，博士，副研究员，主要研究方向：可测试性设计、低功耗测试与测试压缩、MEMS测试与可靠性设计等。