多元函数的微分及其应用

李晶平

(天津师范大学数学科学学院，天津 300387)

多元函数的微分及其应用

李晶平

(天津师范大学数学科学学院，天津 300387)

以一元函数为例扩展到多元函数,讨论多元函数的全微分,自变量由空间的直线、平面扩展到空间球域.了解全微分后，讨论偏导数的定义及微分和偏导数的关系.多元函数的隐函数是多元函数微分的重要部分,其中会用到偏导数.由多元函数的一阶泰勒公式,引出了应用广泛的Hessian矩阵,从而也导出多元函数的多阶泰勒公式.

偏导数;隐函数;泰勒公式

求多元函数偏导数的方法与一元函数求导方法相类似，只要将n个自变量中的某一个看作变量,其余n-1个看成常量然后对其进行求导便可.多元函数的隐函数可通过雅克比矩阵的非奇异性给出隐函数存在性定理，再由映射知识可推出m个m+n元函数的隐函数.

一、多元函数的全微分

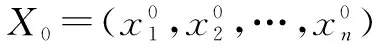
Δy=f(X0+ΔX)-f(X0)=lX0(ΔX)+ο(‖ΔX‖).

(1)

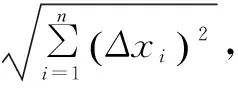
Δy-ο(‖ΔX‖)=dy=lX0(ΔX)=A(Δx1,Δx2,…,Δxn)T=a1Δx1+…+anΔxn.

二、多元函数的偏导数

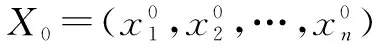
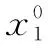
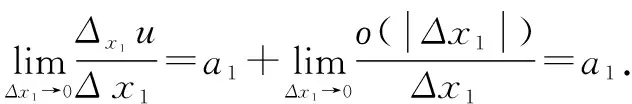
有时也可记作yxi′或fxi′.求多元函数偏导数的方法与一元函数求导方法相同,将n个自变量中的某个看作变量,其余n-1个看作常量,然后对它进行求导.

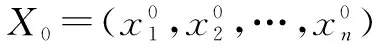
注：上述定理的逆定理不成立,可微能推出偏导数存在,但偏导数存在不能确定函数是否可微.

三、多元函数的隐函数

一元函数解析表达式有显示和隐式两种,设D和E为R的两个区域,二元函数f(x,y)在D×E上有定义,若是对于任意一点x∈D,存在唯一一个y∈E使得f(x,y)=0,这样我们就说方程f(x,y)=0确定了一个由D到E的隐函数,或者说由f(x,y)=0,可解出y=u(x),即f(x,u(x))=0,∀x∈D.同理,对多元函数来说有时也可用方程F(x1,x2,…,xn,y)=0来确定隐函数.但是每个多元函数它们都存在隐函数吗，若存在隐函数又该满足什么条件，下面将给出隐函数存在的定理.

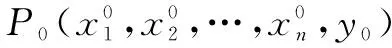
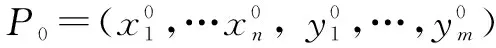
四、多元函数的泰勒公式

设n元函数y=f(X)=f(x1,x2,…,xn)在点X0可微，则在点X0附近的y可表示为

f(X)=f(X0)+f(X0)·ΔX+ο(‖ΔX‖)，

其中ΔX=X-X0,f(X0)=(…,

1.多元函数的一阶泰勒公式

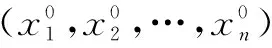
(3)

其中X=X0+ΔX,ΔX=(Δx1,Δx2,…,Δxn)T,

则(3)式称为一阶泰勒公式,H为f的Hessian矩阵.

2.多元函数的多阶泰勒公式

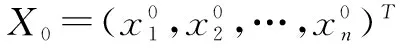
例求f(x,y)=xy在点(1,4)的二阶Taylor公式,并用它计算(1.08)3.96.

解fx(x,y)=yxy-1,fy(x,y)=xylnx,fx2(x,y)=y(x,y)xy-2,fy2(x,y)=xy(lnx)2.

将上面的式子代入泰勒公式后,xy=1+4(x-1)+6(y-1)+6(x-1)2+(x-1)(y-4)+ο(ρ2).

略去余项后令x=1.08,y=3.96,则有(1.08)3.96≈1+4×0.08+6×(1.08)2-0.08×0.04=1.3552.

本文探讨了多元函数的微分及其应用,从多元函数的全微分开始,研究了其偏导数和高阶偏导数与微分的关系.通过研究其偏导数引出多元函数的隐函数,进而将其隐函数广泛应用到几何问题求解中.通过多元函数的泰勒公式,能更好地解决复杂函数,更能为复杂计算提供良好方法.

[1]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2010.

[2]马富民,高文杰.数学分析(第二册)[M].北京:高等教育出版社,2005.

G632

A

1008-0333(2017)22-0010-02

2017-06-01

李晶平(1992.9-)，女，汉族，山西忻州人，研究生在读,助教，从事科学技术史.

责任编辑：杨惠民]