地铁牵引回流系统的钢轨电位和杂散电流仿真
,,,,,
(福建工程学院 信息科学与工程学院,福建 福州 350118)
地铁牵引回流系统的钢轨电位和杂散电流仿真
何涛,李培强,王璜,汪俊民,陈思宇,谢辉煌
(福建工程学院 信息科学与工程学院,福建 福州 350118)
地铁钢轨电位异常导致的钢轨电位限制装置频繁动作是目前地铁牵引回流系统运行过程普遍存在的问题。通过建立单边供电单车行驶的数学模型,结合电路中的叠加原理建立双边供电回流系统单车、多车行驶时的数学模型,在Matlab平台上对单、双边以及线路全程稳态运行的地铁牵引回流供电系统模型分别进行仿真,获取地铁正常运行下钢轨电位和杂散电流的分布曲线,通过仿真图形对比,分析钢轨电位和杂散电流的影响因素,为地铁合理运营与规划提供理论依据。
牵引回流系统; 钢轨电位; 杂散电流; 影响因素
地铁牵引回流供电系统一般用走行轨钢轨作为牵引列车电流的回流通道,但钢轨并不能做到完全绝缘,在实际运行中存在部分电流泄露到大地中。泄露电流经过钢轨和大地之间的电阻称为过渡电阻。泄露电流在过渡电阻上产生的电压,即为钢轨电压。因此,列车牵引电流一部分由钢轨回到牵引变电所负极,另外一部分则是泄露进入大地再回到牵引变电所负极,这部分泄露电流即为杂散电流。钢轨电压的异常不仅对地铁的设备信号产生影响而且可能对乘客的人身安全构成威胁,由此产生的杂散电流,也会对地铁土建结构的钢筋、设备金属外壳以及地下金属管线产生腐蚀,降低了结构的耐久性和使用寿命[1]。文献[2]指出南京地铁一号线在运营时轨道电压过高导致轨道电位限制装置达到永久合闸接地位置,造成钢轨与大地之间的电流达到800 A以上,这将会对地铁土建结构的钢筋及地下金属管道等造成严重的电腐蚀。文献[3]指出单边供电模型下钢轨电压和杂散电流的分布情况。文献[4]指出,钢轨电压与供电方式、列车数量有关。文献[5]指出过渡电阻对杂散电流分布的影响。但是牵引回流系统在某一时刻多辆列车在位置、工况、大地环境不同的时候,情况非常复杂,不是只考虑单一影响因素就能准确反应钢轨电位和杂散电流的分布情况。基于这种情况,通过建立单边供电回流系统下数学模型[6-8],推导出牵引电流、钢轨电流和杂散电流三者间的关系,并在此基础上结合电路中的叠加原理对地铁全线运行时多列车供电回流系统模型进行仿真获得钢轨电压和杂散电流的分布曲线,并分析出二者的影响因素。
1 地铁单边供电单车行驶时钢轨电压和杂散电流的数学模型
假设以牵引变电所的位置为坐标原点,列车运行方向为正方向,列车距牵引变电所的距离为L,某一时刻列车获取的电流为I,如图1所示。

图1 单边供电单车行驶时供电示意图Fig.1 Single vehicle power supply schematic with unilateral power supply
假设走行轨纵向电阻Rg、走行轨相对大地的过渡电阻Rj和大地电阻Rd均匀分布。图1中选取任意一段,设Rg是走行轨的纵向电阻,单位是Ω/km;Rj是走行轨对大地的过渡电阻,单位是Ω/km;x是计算点至牵引变电所的距离,单位是km;i(x)是走行轨在x处回牵引变电所的电流,单位是A;ie(x)是泄露到大地的杂散电流,单位是A;u(x)是走行轨相对于大地的地位差,单位是V;I是地铁机车在从牵引网上获取的电流,单位是A。将线路各区域分割成许多微分段dx,每一微分段的长度为无穷小,则钢轨-大地的电压分布模型和电流分布模型分别如图2、3所示。
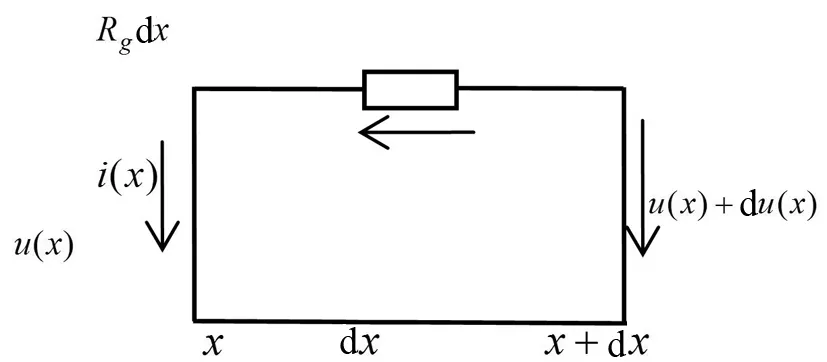
图2 电压分布模型及参数Fig.2 Voltage distribution model and parameters
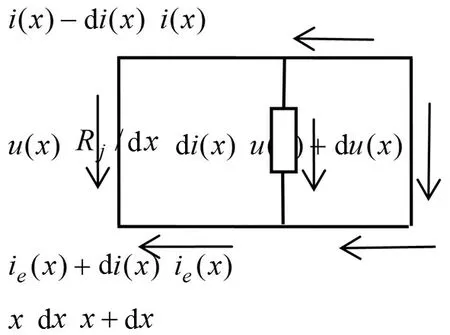
图3 电流分布模型及参数Fig.3 Current distribution model and parameters
则由图2、3可得:
可求得通解:

以牵引变电所为坐标原点,列车前行方向为x轴正方向,则有边界条件:I(L)=I。求出C1、C2。最终可以求出走行轨对地电压u(x)、走行轨电流i(x)和杂散电流ie(x)。
其中牵引电流、钢轨电流与杂散电流的关系:
2 地铁双边供电时钢轨电压和杂散电流的数学模型
综合考虑地铁单边供电时的基本原理、实际建设中的供电方式以及运行过程中的行车密度,文章分别分析了双边供电情况下单车行驶和多车行驶的牵引回流系统的钢轨电压和杂散电流的数学模型。
2.1 双边供电单车行驶时钢轨电压和杂散电流的数学模型
正常情况下双边供电,相邻的两座牵引供电所作为区段内运行列车的电源。假设以牵引变电所1作为坐标原点,相邻两座牵引变电所之间的距离为L,列车行驶方向为x轴正方向,列车距牵引变电所1的距离为L1,距牵引变电所2的距离为L2,从接触网获取的电流为I,如图4所示。假设走行轨纵向电阻Rg、走行轨相对大地的过渡电阻Rj和大地电阻Rd均匀分布。根据单边供电单车行驶时的计算原理,运用的微分等值法计算出的走行轨对地电压u(x)和杂散电流ie(x)。
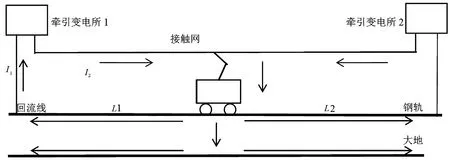
图4 双边供电单车行驶时供电示意图Fig.4 Single vehicle power supply schematic with bilateral power supply
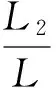
2.2 双边供电多车行驶时钢轨电位和杂散电流的数学模型
正常情况下双边供电,相邻的两座牵引变电所作为区段内列车的电源。假设以牵引变电所1作为零点,相邻两座牵引变电所距离为L,列车行驶方向为x轴正方向,列车距离牵引变电站1的距离分别是L11、…、Lk1、…、Ln1(L1<… 图5 双边供电多车行驶时供电示意图Fig.5 Multi-vehicle power supply schematic with bilateral power supply 3.1 单、双边供电轨道电位和杂散电流的仿真对比 设两变电所之间的距离为4 km,列车牵引电流I=1 000 A,列车位置取1.5、3 km,钢轨纵向电阻Rg=0.06 Ω/km,钢轨与大地的过渡电阻Rj=3 Ω/km。钢轨电位和杂散电流分布曲线如图6~9所示。 图6 列车位置1.5 km时钢轨电压分布曲线Fig.6 The distribution curve of rail voltage at a driving distance of 1.5 km 图7 列车位置1.5 km时杂散电流的分布曲线Fig.7 The distribution curve of stray current at a driving distrance of 1.5 km 图8 列车位置3 km时钢轨电压分布曲线Fig.8 The distribution curve of rail voltage at a driving distance of 3 km 图9 列车位置3 km时杂散电流的分布曲线Fig.9 The distribution curve of stray current at a driving distance of 3 km 仿真曲线表明:(1)无论单边供电方式还是双边供电方式,牵引变电所所在位置的轨道电压均为负值且达到最小,杂散电流均为零;列车位置处的轨道电压均为正且达到最大值,杂散电流也为零。(2)双边供电方式下的轨道电压与杂散电流数值的绝对值均比单边供电方式下要小,并且列车运x位置与牵引变电所的位置距离越远,双边供电方式下的数值落差也比单边方式要低。(3)双边供电方式下列车在两个牵引变电所正中间时轨道电压的数值最大;但列车运行的位置对杂散电流最大值的变化影响不大。 3.2 列车全线运行时钢轨电位和杂散电流的仿真对比 从上文2.1~2.2节建模获得的数学公式,基于某实际运行的地铁线路,利用MATLAB编程,选取线路上列车密度最大的时刻,对钢轨电位和杂散电流等量进行仿真分析,假设牵引变电站位置分别位于2.425、6.716、9.858、13.725、17.310、21.445 km处,列车位置分别位于1.054、3.500、5.514、7.818、10.521、12.420、14.840、18.000、19.920、20.910、23.210 km处。在仿真过程中不考虑再生制动,只考虑单行线,忽略相邻变电所的影响。 (a)设仿真时钢轨纵向电阻Rg=0.06 Ω/km,钢轨与大地的过渡电阻Rj=3 Ω/km,线路全长25 km。列车负荷电流大小如表1所示。则钢轨电位和杂散电流的分布曲线如图10、11所示。 表1 列车负荷电流大小Tab.1 The load current of vehicle 图10 不同负荷电流条件下的全线钢轨电位分布曲线Fig.10 The potential distribution curve of the whole rail under different load currents 图11 不同负荷电流条件下全线杂散电流分布曲线Fig.11 The distribution curve of stray current across the line under different load currents (b)设仿真时轨道电阻Rg取值分别是0.02、0.06、0.08 Ω/km,钢轨与大地的过渡电阻Rj=3 Ω/km,线路全长25 km,则钢轨电位和杂散电流的分布曲线如图12、13所示。 图12 不同轨道电阻条件下全线钢轨电位分布曲线Fig.12 The potential distribution curve of the whole rail under different track resistances (c)设仿真时钢轨与大地的过渡电阻Rj分别取0.4、3、15 Ω/km,轨道电阻Rg=0.06 Ω/km,线路全长25 km,则钢轨电位和杂散电流的分布曲线如图14、15所示。 由图10-15仿真曲线的结果表明:1)无论是单、双边供电,还是相邻变电站之间列车数量的变化,轨道电位和杂散电流都随着列车负荷电流的变大而变大。2)无论是单、双边供电,还是相邻变电站之间列车数量的变化,轨道电位和杂散电流都随着轨道电阻Rg的变大而变大。3)无论是单、双边供电,还是相邻变电站之间列车数量的变化,轨道电位基本随着大地纵向电阻变化而基本保持不变;杂散电流随着大地纵向电阻的变小而变大。 图13 不同轨道电阻条件下全线杂散电流分布曲线Fig.13 The stray current distribution curves under different track resistances 图14 不同过渡电阻条件下全线钢轨电位分布曲线Fig.14 The potential distribution curve of the whole rail under different transition resistances 图15 不同过渡电阻条件下全线杂散电流分布曲线Fig.15 The stray current distribution curve under different transition resistances 通过建立理想的单边供电回流系统下单车运行模型,推导出钢轨电压与牵引电流、列车运行距离的函数关系,并基于叠加原理建立双边供电系统单、多车运行模型。在MATLAB平台上仿真出钢轨电位和杂散电流的分布曲线。并以此分析出列车的钢轨电位与杂散电流不仅受到供电方式、列车运行位置、列车运行密度的影响,还受列车负荷电流、轨道电阻和大地纵向电阻等因素的影响。 [1] 张栋梁.城市轨道交通直流牵引回流系统防护技术研究[D].徐州:中国矿业大学,2012. [2] 苗因山.轨电位限制装置拒动导致框架保护故障[J].都市快轨交通,2008,21(3):92-94. [3] 王猛.直流牵引供电系统钢轨电位与杂散电流分析[J].城市轨道交通研究,2005,8(3):24-26. [4] 安娜,吴积钦,梁奎.直流牵引供电系统轨道电位影响因素的分析[J].电气化铁道,2014,25(4):21-24. [5] 蔡力,王建国,樊亚东,等.地铁走行轨对地过渡电阻杂散电流分布的影响[J].高电压技术,2015,41(11):3604-3610. [6] 李国欣.直流牵引回流系统分析及轨电位相关问题研究[D].北京:中国矿业大学,2010. [7] 杨迪.城市轨道交通杂散电流实验系统设计与仿真[D].成都:西南交通大学,2013. [8] Liu Chongru,Zhang Boming,Hou Yunhe.An improved approach for AC-DC power flow calculation with multi-infeed DC Systems[J].IEEE Transactions on Power Systems,2011,26(2):862-869. (责任编辑:肖锡湘) Simulationofrailpotentialandstraycurrentinmetrotractionreturnsystem He Tao,Li Peiqiang,Wang Huang,Wang Junmin,Chen Siyu,Xie Huihuang (College of Information Science and Engineering,Fujian University of Technology,Fuzhou 350118,China) The frequent action of rail potential limiting devices caused by the potential abnormality of metro rail is presently a common problem in the operation of the traction power return system of the metro.A mathematical model of unilateral power supply single vehicle/train driving was first constructed,then a mathematical model of bilateral power supply return system single and multi vehicle driving was established based on the principle of superposition circuit.Simulations were conducted via the MATLAB platform,covering the single,bilateral and the whole subway line stable operation of the traction power return system models.The distribution curves of the rail potential and stray current of the metro power supply return system under the normal operation of the metro were obtained.A comparative analysis of the influential factors on the rail potential and stray current was performed to provide a theoretical basis for the reasonable operation and planning of the Metro. traction power return system;rail potential;stray current;influencing factors U231.94 A 1672-4348(2017)04-0386-07 10.3969/j.issn.1672-4348.2017.04.016 2017-07-16 国家自然科学基金资助项目(51677059) 李培强(1975-),男,山西忻州人,教授,硕导,博士,研究方向:电力系统运行与控制及负荷建模。
3 算例仿真及分析


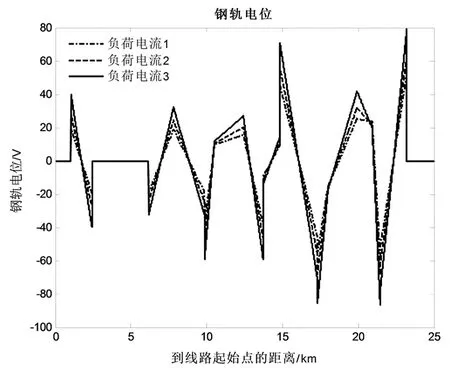
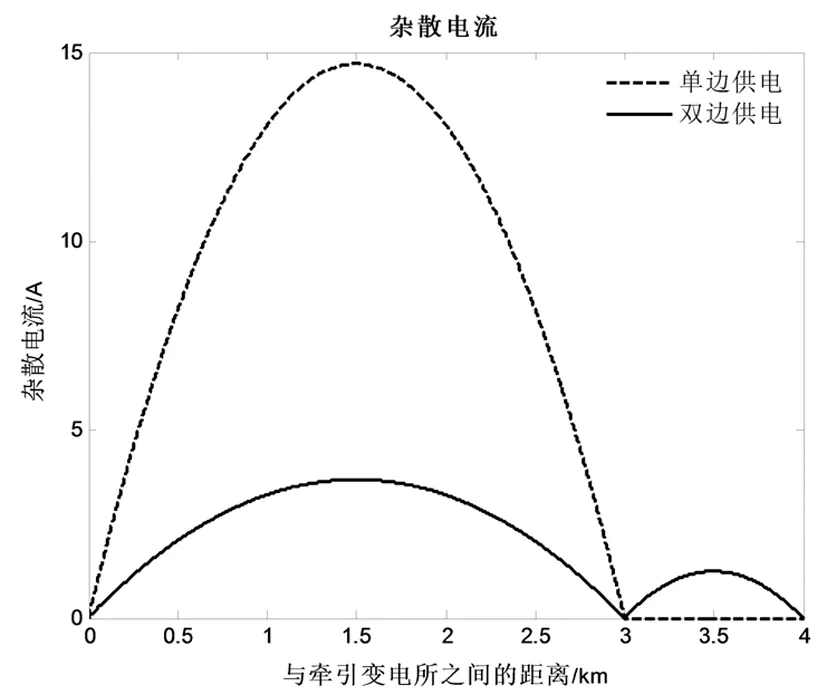

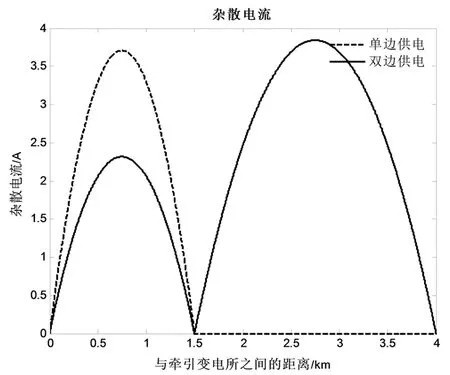
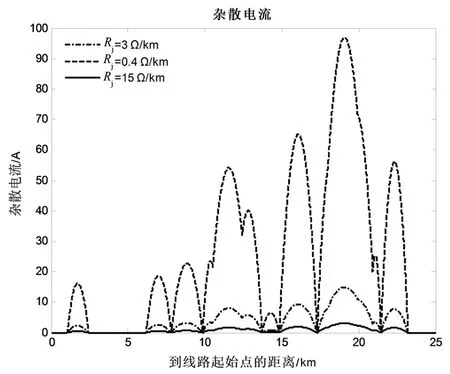
4 结论

