面齿轮磨削工艺参数优化的试验研究
刘金华,龙 誉,方曙光,明 瑞
(湖南工业大学 机械工程学院,湖南 株洲 412007)
面齿轮磨削工艺参数优化的试验研究
刘金华,龙 誉,方曙光,明 瑞
(湖南工业大学 机械工程学院,湖南 株洲 412007)
基于蝶形砂轮磨削正交面齿轮的正交试验,分析了面齿轮各磨削工艺参数,包括磨削深度ap、砂轮转速vs、刀具进给速度vw等,对表面粗糙度Ra、磨削变质层深度h和磨除率Zw的影响规律,得到了磨削优化工艺参数。根据正交试验结果,利用回归分析方法分别建立了表面粗糙度Ra、磨削变质层深度h和磨除率Zw的回归数学模型。试验结果表明,所求得模型具有良好的精度,可以为面齿轮磨削质量和效率的提高提供一定的理论依据。
面齿轮磨削;表面粗糙度;变质层深度;磨除率;正交试验;回归数学模型
1 研究背景
面齿轮传动是一种圆柱齿轮与圆锥齿轮啮合的新型齿轮传动结构,具有结构简单、重合度大、传动稳定、质量轻和传动比较大等诸多优点。目前,面齿轮传动在国外已经被广泛应用,如美国NASA(National Aeronautics and Space Administration)已将面齿轮传动副成功地应用于直升机主减速器大功率动力传动中,发挥了其独特的优越性[1]。但是目前国内面齿轮的加工精度不高且生产效率较低,从而制约了面齿轮的发展和广泛应用。面齿轮精加工的主要工艺是磨削加工,磨削加工质量会影响面齿轮的硬度、表面粗糙度和使用寿命。因此,选择合理的磨削工艺参数可以提高面齿轮质量和生产效率,从而对面齿轮的应用有着重要作用。
W. Bouzid[2]通过优化高速切削工艺参数以提高面齿轮加工效率;Ho W. H. 等[3]为降低面齿轮表面粗糙度,运用正交试验和遗传算法,对工艺参数进行了优化,从而使构造的数学模型对表面粗糙度值的预报误差达到4.06%;张慧鹏[4]利用MATLAB优化工具箱,对无心磨削工艺参数进行了优化,以实现单位时间内磨除率最大,得到了最佳的磨削参数,简化了复杂的编程,提高了设计的效率和质量;丁军鹏[5]通过分析不同阶段主要磨削工艺参数的影响,对齿轮不同磨削阶段的工艺参数进行了优化设计,建立了不同阶段的优化目标函数,并运用MATLAB进行了优化计算,获得了较好的磨削表面质量和较高的磨削率,为生产效率和磨削质量的提高提供了理论依据;戴娟等[6]就外圆磨加工外圆时的工艺参数优化问题进行了讨论,将最优工艺参数的二维有约束的优化问题转化为一维有约束优化求解,通过优化工艺参数,在保证表面质量的前提下,降低了磨削加工成本。目前,国内外对于面齿轮磨削工艺参数优化的研究相对较少。
本文以面齿轮齿面粗糙度、轮齿变质层深度和单位时间内磨除材料的体积(磨除率)作为评价磨削表层性态和加工效率的主要指标,通过正交试验系统地研究磨削工艺参数包括砂轮转速、磨削深度和刀具进给速度对3个评价指标的影响规律,得到了面齿轮磨削工艺参数优选组合方案,并建立了较为准确的评价指标回归模型[7],可为面齿轮精加工工艺提供一定的理论参考。
2 面齿轮磨削试验条件与设计
2.1 磨削工艺条件
由于面齿轮的齿面是复杂曲面,在普通的磨床上很难精确地完成其曲面的成型运动。因此,本文使用五坐标数控磨齿机对外径为170 mm、内径为143 mm的面齿轮进行精加工,采用300 mm的普通碟形砂轮展成磨削并且采用水基合成磨削液。面齿轮材料选用20CrMnTi,其具体的几何参数如表 1所示。
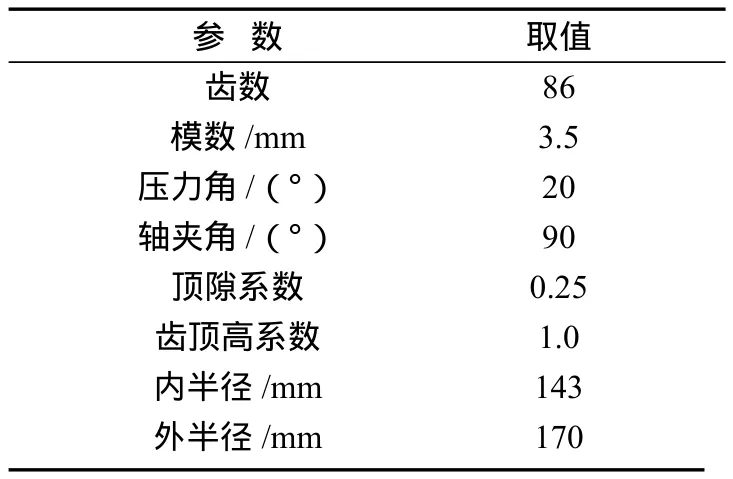
表1 正交面齿轮几何参数Table 1 Geometric parameters of orthogonal face gears
2.2 检测仪器与评价指标
1)表面粗糙度Ra
选用粗糙度轮廓测量仪Hommel T8000 RC,对面齿轮齿面粗糙度Ra值进行测量。每次取样长度为0.25 mm,检测距离为2 mm,探针以0.15 mm/s的速度移动,以3次测量值的平均值作为粗糙度的实际值[8]。
2)磨削变质层深度h
为方便、精确地测量面齿轮样品硬度,选用全自动显微硬度计LECO-AMH43对面齿轮硬度进行测量,根据硬度的变化值,可得到变质层深度值。在试样表层加荷4.8 N,加载时间为13 s,以距离表层0.1 mm处为测量起点,每隔0.2 mm测量一次,将相同位置的3次测量结果平均便可得到硬度值[7]。
3)磨除率Zw
选用高精度的数显千分尺检测磨削厚度,在磨床进给系统上安装定位块,通过进给数显系统,测量砂轮磨除厚度,然后计算出磨除率[7]。
2.3 磨削正交试验设计
影响面齿轮磨削表层性能和加工效率的因素很多,需要选择合适的磨削工艺参数进行研究,以获得较好的表层性能和较高的加工效率。本文选用ap(磨削深度)、vs(砂轮转速)和vw(刀具进给速度)作为试验的3个因素,将设备精度误差、磨削振动以及冷却条件等因素视为通常水平;以Ra(表面粗糙度)、h(磨削变质层深度)和Zw(磨除率)为试验评价指标。每个因素取3个水平值,试验的各因素及水平如表2所示。

表2 磨削正交试验因素和水平Table 2 Factors and levels of grinding orthogonal tests
由于多因素试验间的组合比较多,需要耗费大量的时间与经费,因此本试验选用L9(33)正交表。根据表2的3因素、3水平,对面齿轮进行磨削试验,记录9组试验数据,如表3所示。
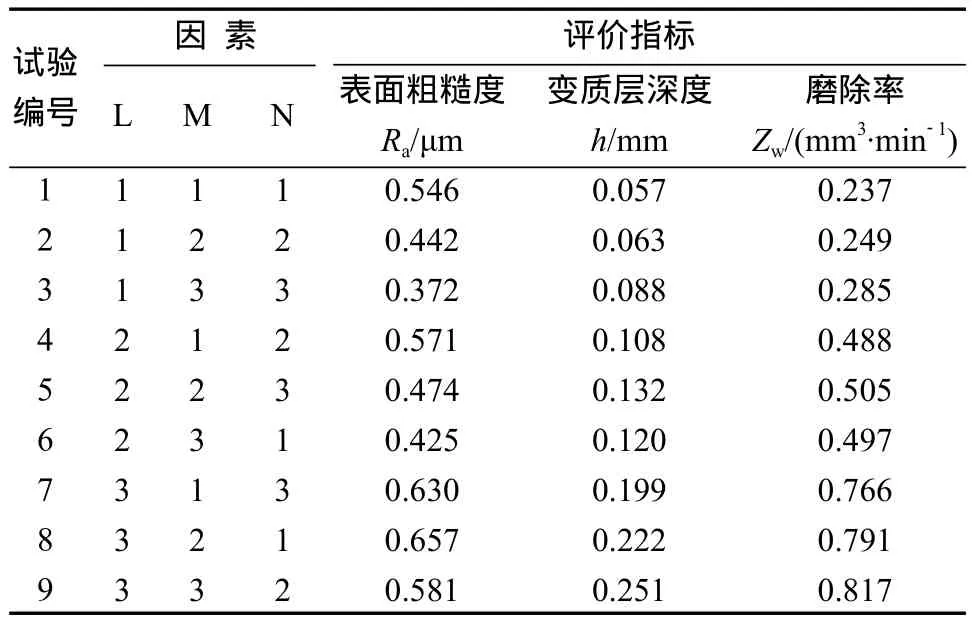
表3 磨削正交试验数据Table 3 Orthogonal grinding test data
3 面齿轮磨削正交试验分析与工艺参数优选
3.1 极差分析法
正交试验设计和分析方法大致分为2种:一种是极差分析法,另一种是方差分析法。极差分析法简单易懂,实用性强,在设计研究中得到了广泛应用[9]。下面通过极差分析法分别计算各因素对单一试验评价指标的影响程度,即磨削深度ap、砂轮转速vs和刀具进给速度vw分别对表面粗糙度Ra、变质层深度h和磨除率Zw的影响。
极差分析法的计算与判断,可直接在试验数据表3上进行。对表面粗糙度Ra、磨削变质层深度h和磨除率Zw3个试验评价指标的极差计算结果和优选组合方案的选取,分别见表4~6。

表4 磨削表面粗糙度极差分析结果Table 4 Results of range analysis of grinding surface roughness
以上各分析结果表中,Ki分别表示因素ap,vs,vw的第i(i=1, 2, 3)个水平所对应的评价指标值之和,ki为i水平的平均值。R为任一列因素的极差,R=max{k1,k2,k3}-min{k1,k2,k3},即同一列中k1,k2,k3这3个数中最大者减去最小者。
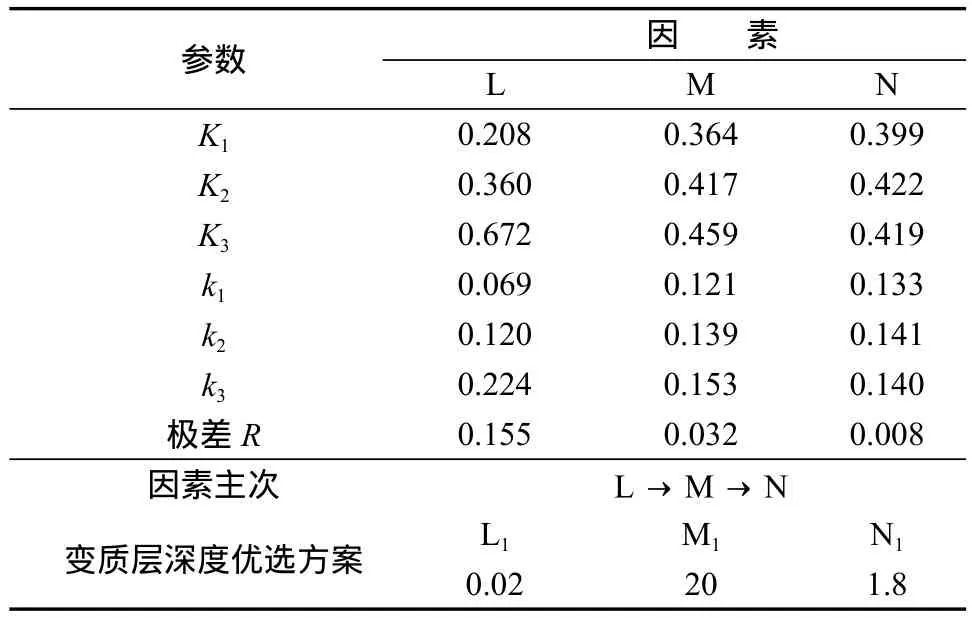
表5 磨削变质层深度极差分析结果Table 5 Results of range analysis of grinding metamorphic layer depth

表6 磨削磨除率极差分析结果Table 6 Results of range analysis of grinding removal rate
各列的极差值不同,反映了因素水平的变化对试验指标的影响程度。极差值越大,所对应的因素对试验指标的影响越大,因此,可以依据极差值判断因素的主次。
ki值的大小反映了该因素各水平对试验指标的影响,用于判断因素水平的最优选组合方案。由于试验评价指标Ra和h越小越好,所以应取各列中ki的最小值所对应的水平;而试验指标Zw越大越好,故应取各列中ki的最大值所对应的水平。
从表4~6的极差值大小顺序可看出,因素主次是相同的,即对Ra(表面粗糙度)影响最大的是ap(磨削深度),其次是vs(砂轮转速),最不显著的是vw(刀具进给速度)。
分析表4中的数据可以得出,在砂轮转速和刀具进给速度不变的情况下,随着磨削深度的逐渐增大,面齿轮的表面粗糙度逐渐增大,其原因是单颗磨粒的最大切削厚度增大,导致齿轮磨削材料的塑性变形随之增大,此时磨粒切削刃在齿轮表面的切痕深度增加,从而使面齿轮表面变得更加粗糙。当磨削深度和刀具进给速度不变时,随着砂轮转速的增大,面齿轮的表面粗糙度随之减小。当磨削深度和砂轮转速不变时,随着刀具进给速度的增大,面齿轮的表面粗糙度随之变小。
根据同一列ki值的大小,选择对应的工艺参数优选组合应为L1M3N3,这样的方案能保证面齿轮磨削加工时具有良好的表面粗糙度。
由表5可知,在砂轮转速和刀具进给速度不变的情况下,随着磨削深度的增大,变质层深度增大。在磨削深度和刀具进给速度不变的情况下,随着砂轮转速的增大,变质层深度随之增大。在实际加工中,应尽量减少或消除变质层,因此工艺参数优选组合应为L1M1N1。
由表6可以得知,在砂轮转速和刀具进给速度不变的情况下,随着磨削深度的增大,磨除率随之增大。在磨削深度和刀具进给速度不变的情况下,随着砂轮转速的增大,磨除率随之增大。由于磨除率直接反映了加工的效率,因此工艺参数优选组合方案为L3M3N3。
3.2 综合平衡法
由3.1节中的极差分析法可知,3个因素ap,vs,vw对各指标Ra,h和Zw的影响程度不同。为了兼顾各个指标,找出使每个指标都尽可能好的试验条件,因此再采用综合平衡法[10]进行分析。
1)确定评价指标集和影响函数集
以Ra,h和Zw为评价指标集U={Xmn},其中m=1,2, 3分别为表2中的3个因素,n=1, 2, …, 9表示表3中的试验编号,各指标的评价集为V={Y1n,Y2n,Y3n}。
2)建立隶属函数
建立评价指标集U对评价集V的隶属函数,根据计算得出的隶属度值与该指标在综合评价中的重要程度相匹配。其中,表面粗糙度Ra和变质层深度h为偏小型指标,磨除率Zw为偏大型指标,因此建立隶属函数:
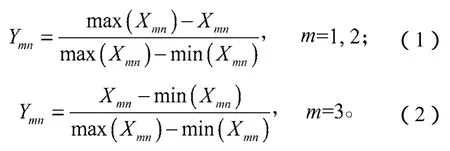
3)确定权重分配集
为了反映各指标的重要程度,引入权重分配集A={r1,r2,r3}。在面齿轮磨削过程中,表面粗糙度的重要程度较高,其权重r1取0.4;变质层深度对控制磨削表面质量也有一定作用,其权重r2取0.2;磨除率是保证生产效率的主因,其权重r3取0.4。因此A={0.4, 0.2, 0.4}。
设采用综合平衡法得到的综合评价指标集为P={Tn},它反映各个指标的综合影响程度。

式中Smn表示各个试验指标的影响函数。
将表3中的各评价指标值代入式(3),得到磨削综合评价指标值,如表7所示。

表7 磨削综合评价指标值Table 7 Comprehensive evaluation indicator values of grinding
对表7所示指标值进行极差分析,所得结果如表8所示。由表8所示因素主次可以得知,综合影响规律与单因素的极差分析结果一致,即磨削深度ap对3个评价指标都有较显著的影响。由综合平衡法极差分析可得最终的优选方案为L2M3N3,即磨削深度ap=0.06 mm,砂轮转速vs=65 r/s,砂轮摆动进给速度vw=6.0 m/min。
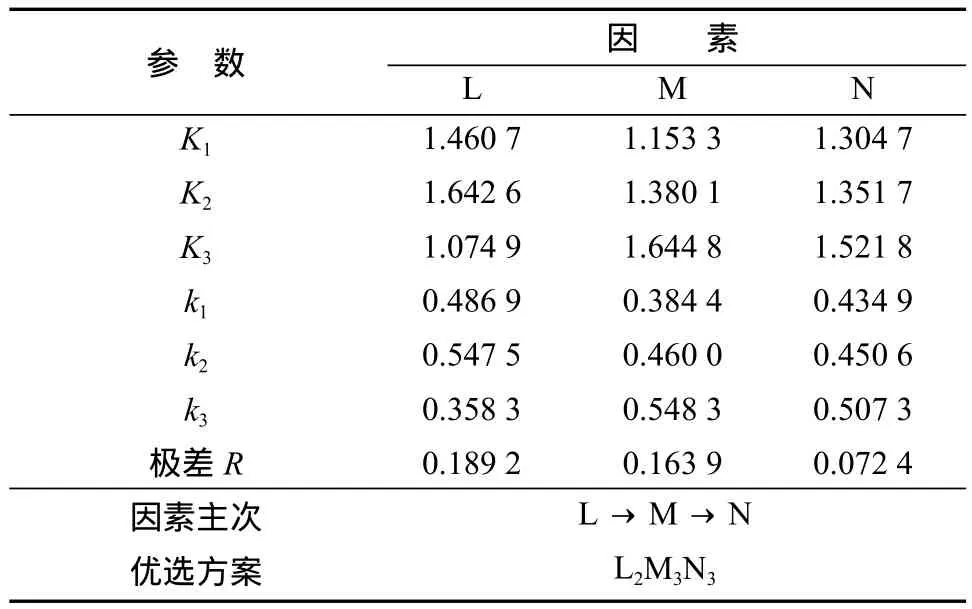
表8 综合平衡法极差分析结果Table 8 Results of range analysis of integrated balance method
4 面齿轮磨削试验指标的回归模型与试验验证
4.1 建立面齿轮磨削试验指标的回归模型
采用建模方便、拟合精度较好的幂函数来建立回归模型。对于粗糙度回归模型可设

该线性方程共包含x1,x2,x33个自变量,试验结果用y表示。考虑存在试验误差ε,故由9组试验数据可建立如下多元线性回归方程

根据式(9)可得c=e0.7552,k=0.183 6,q=-0.211 9,t=-0.083 7,代入式(4)得到的磨削表面粗糙度Ra的回归模型为
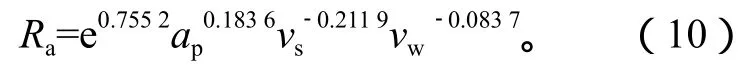
用同样的方法可求得变质层深度与磨除率的回归模型:

4.2 面齿轮磨削试验指标回归模型的试验验证
运用回归模型公式(10)~(12),分别对Ra,h,Zw进行计算,产生最大误差时对应的试验编号和相应结果如表9所示。

表9 最大误差时对应的回归计算值与试验值比较Table 9 Corresponding regression values compared with the experimental ones with the maximum error
由表9可知,根据回归模型得到Ra,h,Zw的计算值与相应试验的测量值之间的最大相对误差值分别为17.4%, 22.5%, 8.7%。误差产生的主要原因是磨削加工面齿轮的过程比较复杂,回归模型只考虑了磨削工艺中3个因素对指标的影响,并未考虑设备精度误差、磨削振动以及冷却条件等因素的影响,但以上因素对相对误差的影响不大。表9表明,由回归模型计算所得结果的相对误差在合理范围内。因此,可利用回归模型选择合理的磨削参数,以达到较好的表面磨削质量和较高的磨削效率。
5 结论
1)通过对正交面齿轮的正交试验,获得了磨削工艺参数对面齿轮磨削表面性态(Ra,h)和加工效率(Zw)的影响规律:影响最显著的因素是磨削深度ap,随着磨削深度的增加,上述3个评价指标值相应增大。
2)通过运用综合平衡法的极差分析可得知:当ap=0.06 mm、vs=65 r/s、vw=6.0 m/min时,面齿轮的表面性态较好,并且磨削效率较高,即最佳工艺方案为L2M3N3。
3)通过采用多元非线性回归分析法,分别建立了Ra(表面粗糙度)、h(变质层深度)和Zw(磨除率)的回归模型。利用数学模型对Ra,h,Zw进行回归计算,获得误差最大的试验号,将其与对应的试验测量值进行比较,相对误差值分别为17.4%, 22.5%, 8.7%,说明建立的回归模型的精度良好,可在磨削加工前利用该模型选择合适的磨削工艺参数,以提高面齿轮质量和生产效率。
[1]LITVIN F L,FUENTES A,ZANZI C,et al. Design,Generation, and Stress Analysis of Two Versions of Geometry of Face-Gear Drives[J]. Mechanism and Machine Theory,2002,37(10):1179-1211.
[2]BOUZID W. Cutting Parameter Optimization to Minimize Production Time in High Speed Turning[J]. Journal of Materials Processing Technology,2005,161(3):388-395.
[3]HO W H,TSAI J T,LIN B T,et al. Adaptive Network-Based Fuzzy Inference System for Prediction of Surface Roughness in End Milling Process Using Hybrid Tagnchi-Genetic Learning Algorithm[J]. Export Systems with Applications,2009,36(2):3216-3222.
[4]张慧鹏. 基于MATLAB的无心磨削参数工艺优化[J].组合机床与自动化加工技术,2009(10):85-87.ZHANG Huipeng. Process Parameter Optimization of Centerless Grinding Based on MATLAB[J]. Modular Machine Tool & Automatic Manufacturing Technique,2009(10):85-87.
[5]丁军鹏. 齿轮成形磨削工艺参数优化及试验研究[D].洛阳:河南科技大学,2011.DING Junpeng. Optimization and Experimental Research on Gear from Grinding Process Parameters[D].Luoyang:Henan University of Science and Technology,2011.
[6]戴 娟,胡冠昱,高全芹. 外圆磨磨削工艺参数的优化设计[J]. 机械设计与制造,2008(8):131-132.DAI Juan,HU Guanyu,GAO Quanqin. Optimization Design for the Craft Parameter of Cylindrical Grinder[J].Machinery Design & Manufacture,2008(8):131-132.
[7]龙 誉. 面齿轮磨削工艺参数优化研究[D]. 株洲:湖南工业大学,2016.LONG Yu. Optimization of the Technology Parameters of Face-Gear from Grinding[D]. Zhuzhou:Hunan University of Technology,2016.
[8]MING X Z,GAO Q,YAN H Z,et al.Mathematical Modeling and Machining Parameter Optimization for the Surface Roughness of Face Gear Grinding[J].The International Journal of Advanced Manufacturing Technology,2017,90(9/10/11/12):2453-2460.
[9]杜金萍. 基于模糊综合评价的磨削过程优化研究[J].煤矿机械,2008,29(7):55-57.DU Jinping. Research on Optimization of Grinding Process Based on Fuzzy Synthetic Evaluation[J]. Coal Mine Machinery,2008,29(7):55-57.
[10]蒋大军. 采用多元非线性回归预测钒钛烧结矿强度[J].烧结球团,2006,31(2):5-10.JIANG Dajun. Forecast of Vanadium-Titanium Sinter Strength with Multiple Nonlinear Regression[J]. Sintering and Pelletizing,2006,31(2):5-10.
(责任编辑:邓光辉)
An Experimental Study on the Optimization of Grinding Process Parameters of Face Gears
LIU Jinhua,LONG Yu,FANG Shuguang,MING Rui
(School of Mechanical Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
Based on the orthogonal experiment of grinding orthogonal face gears with butter fl y grinding wheel,an analysis has been conducted on such grinding parameters as grinding depthap, grinding wheel speedvs, and the in fl uence of tool feeding speedvwon surface roughnessRa, grinding depthhand removal rateZw, thus obtaining the optimal grinding process parameters. According to the results of orthogonal test, the regressive mathematical models of grinding surface roughnessRa, metamorphic layer depthhand removal rateZwcan be established by adopting regression analysis method. The results show which testi fi es the better precision of these models, thus providing some theoretical basis for the improvement of grinding gear quality and ef fi ciency.
face gear grinding;surface roughness;metamorphic layer depth;removal rate;orthogonal experiment;regressive mathematical model
TP273
A
1673-9833(2017)04-0014-06
10.3969/j.issn.1673-9833.2017.04.003
2017-05-20
国家自然科学基金资助项目(51375161),湖南省自然科学基金资助项目(2015JJ5018,2017JJ4023)
刘金华(1964-),女,湖南南县人,湖南工业大学教授,主要从事数字化制造技术方面的教学与研究,E-mail:540807051@qq.com
明 瑞(1992-),男,湖南株洲人,湖南工业大学教师,硕士,主要研究方向为数控技术,E-mail:844153340@qq.com

