声振环境下航天器结构应力时程分析

游 进，赖松柏，方 杰

声振环境下航天器结构应力时程分析

游 进，赖松柏，方 杰

（中国空间技术研究院载人航天总体部，北京100094）

航天器发射段严酷的声振环境可能造成薄壁结构上产生一定的裂纹损伤，评估这种裂纹损伤的重要前提是获得结构最大应力的时间历程。针对该问题提出一种航天器结构声振环境下应力时程分析方法。首先基于统计能量分析得到薄壁构件空间平均弯曲应力功率谱，然后基于应力翻倍原则考虑边界条件对应力集中的影响，获得薄壁构件上最大应力的功率谱，最后用随机相位正弦波叠加的方式对最大应力的时间历程进行模拟。针对某载人航天器，采用该方法计算其在发射主动段声振环境下的结构响应，分析其响应特性，得到了密封舱薄壁球底上法兰盘附近最大弯曲应力的时程，并采用雨流计数法对其循环计数特性进行了分析。研究结果可为航天器薄壁结构裂纹损伤评估提供参考。

统计能量分析；声振响应；应力；时间历程

Abstract：The severe vibro-acoustic environment during launch may cause crack damage to thinwalled structures of a spacecraft，and the prerequisite of evaluating such structure damage is the time history of the maximum stress on the structure.An approach analyzing the time history of the spacecraft structure under vibro-acoustic load was presented.First， based on statistical energy analysis，the power spectrum of the spatially averaged flexural stress of thin-walled structure was obtained.Then，the stress concentration due to boundary conditions was accounted for by using the Stress Doubling Rule.Lastly，the random time history of the maximum stress was simulated through the superposition of a series of sinusoidal waves with random phases and amplitudes derived from the spectrum previously obtained.The approach was applied to a manned spacecraft subject to vibro-acoustic load during launch， the time history of the maximum stress near flanges on the habitable module＇s spherical dome，was obtained.The approach proposed offers a basis for the crack damage evaluation of thin-walled structures of spacecraft.

Key words：statistical energy analysis； vibro-acoustic response； stress； time history

1 引言

航天器在发射主动段会经历复杂严酷的声振环境［1-2］，航天器一般采用大量薄壁构件，如载人密封舱主结构金属蒙皮厚度仅2～3 mm，发射主动段的声振环境引起的构件振动易使它们产生一定的裂纹损伤，从而影响结构密封性能甚至导致结构破坏失效［3］，或给其长期在轨服役带来安全隐患，因此评估航天器结构在恶劣声振环境下的裂纹损伤，从而通过结构设计加以控制尤为重要。传统的随机激励下结构失效分析主要基于结构应力功率谱，结合材料疲劳寿命曲线进行随机疲劳损伤累积评估［4-5］，这种方法无法对航天器薄壁构件的裂纹损伤进行分析，后者需基于断裂力学原理考虑单个应力循环造成的裂纹扩展［6］，在掌握构件交变应力时间历程的前提下，可以分析裂纹扩展程度。

用有限元法进行时域分析可得到结构具体位置的应力变化过程，但航天器发射主动段经历的声振环境覆盖中高频，使有限元法的计算量急剧增大，在实际中难以应用，一般采用统计能量分析法进行航天器的声振分析［7-8］。受理论假设的限制，统计能量分析的结果为响应的时间及空间平均值，无法直接作为裂纹损伤评估的依据，给声振环境下航天器结构裂纹损伤评估造成障碍。本文以获取声振环境下航天器薄壁结构的应力时间历程为目的，以统计能量分析作为动响应分析方法，计算航天器薄壁构件弯曲应力的功率谱，并基于应力翻倍原则考虑边界条件对应力集中的影响，最后采用随机相位正弦波叠加的方式获得应力的随机时间序列。将该方法应用于某航天器，分析其在主动段声振环境下的响应特性，针对密封舱球底薄壁构件，得到其应力时间历程估计，并采用雨流计数法对其进行计数统计分析。

2 薄壁结构弯曲应力功率谱

根据统计能量分析原理，对于含m个子系统的复杂声振系统中的子系统i存在如式（1）所示能量平衡方程［9］：

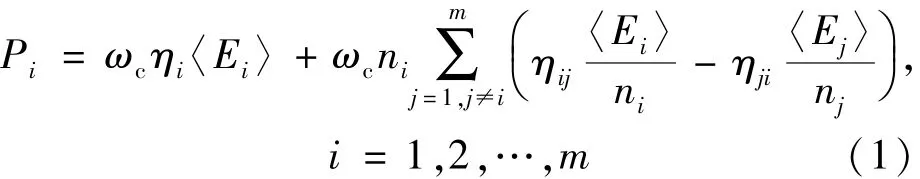
式中，ωc为分析频带的中心频率，〈Ei〉为子系统i的时间平均能量，Pi为外界激励对子系统i的平均输入功率，ηi为子系统i的内损耗因子，ni为子系统i的模态密度，ηij为子系统i与子系统j间的耦合损耗因子。对声振系统的所有m个子系统列出如式（1）的能量平衡方程，通过求解一个线性方程组，可得到所有子系统的稳态能量响应。

稳态激励下，结构／声场子系统的平均应变能／势能与动能相等，则某一子系统的平均总能量为式（2）：

式中，M为子系统质量，〈v2〉为经空间平均的速度均方值。速度均方值可由式（3）所示速度功率谱积分得到：

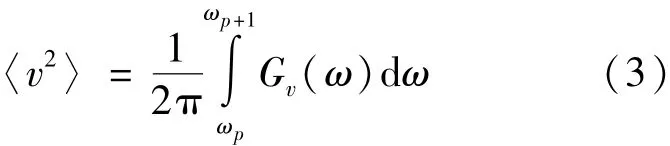
式中，ωp和ωp+1为中心频率为ωc的频带的上下限频率，Gv为速度响应的单边谱。假定Gv在频带［ωp， ωp+1］内为定值 gv，即假定速度为限带白噪声，结合式（2）和（3）得到式（4）：

式中，Δω＝ωp+1-ωp为分析带宽。

若考虑的子系统为薄板结构，弯曲变形时其应变均方值沿截面平均值为式（5）［9］：

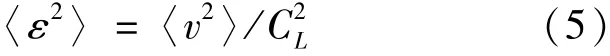
式中，CL＝ D／ρ（1-μ2） 为纵波波速，D为弹性模量，ρ为密度，μ为泊松比。薄壁结构上下表面处的应变最大，其均方值为3〈ε2〉，考虑到应力应变关系 〈σ2〉 ＝ D2〈ε2〉， 得到上下表面处的均方应力为式（6）：

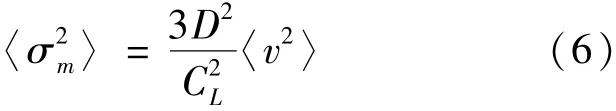
表面应力均方值可由谱积分得到，在［ωp，ωp+1］频段内为式（7）：

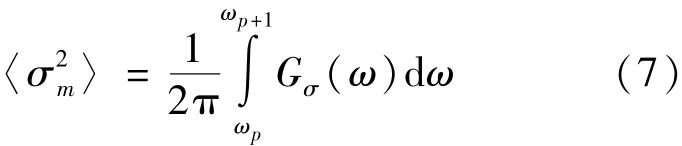
式中，Gσ为应力的单边谱。假定Gσ在频带［ωp， ωp+1］为定值 gσ，将式（7）代入式（6）并考虑到式（3）和（4），得到式（8）：

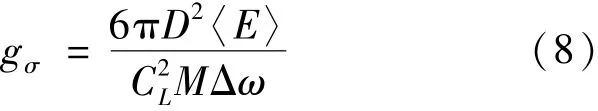
由于统计能量分析基本假设的原因，由应力功率谱得到的应力均方值为空间平均值，实际上声振环境下结构应力随空间位置发生变化，并在边界附近出现应力集中，为根据统计能量分析结果计算结构中出现的最大应力，文献［9］中提出了一种应力翻倍原则（Stress Doubling Rule），即对于某结构，每存在一种边界约束即对空间平均应力均方值乘以2倍，若存在刚性固支边界（包括转角和位移两种约束），最大应力均方值应为平均应力均方值的4倍，若该结构件还存在另外一条边界，且边界间存在相交的情况，则最大应力均方值还应在上述结果基础上乘以2倍。文献［10］指出，应力翻倍原则高估了结构中出现的最大应力，因此根据该原则确定的最大应力将偏于保守。基于上述原理，令结构边界条件引起的应力集中系数为K，得到最大应力的功率谱为式（9）：

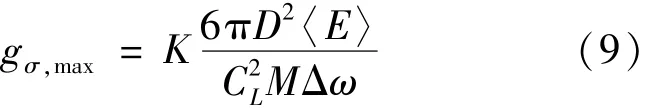
需指出的是，应力翻倍原则是一种经验方法，可用于在未开展试验的情况下或方案设计阶段，对薄壁结构应力集中系数进行预估。

3 应力随机时间历程模拟

采用随机相位正弦波叠加的方法获取应力随机时程。基于应力的单边功率谱gσ，其时域信号x（t）可由式（10）近似获得［11］：

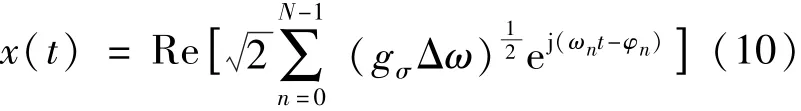
式中，φn～ U（0， 2π），ωn＝ nδω，δω ＝ ωmax／N，ωmax是单边功率谱gσ的频率上限。由于应力相位的频域分布未知，因此假定各频率成分的相角在0到2π上均匀随机分布。

在xk＝x（tk） ＝x（kΔt）处对时域信号采样，其中Δt为采样时间间隔，保证在其功率谱最高频率ωmax对应的一个周期内，采样点的数量不少于两个，即Δt≤π／ωmax。采样得tk时刻的信号为式（11）：

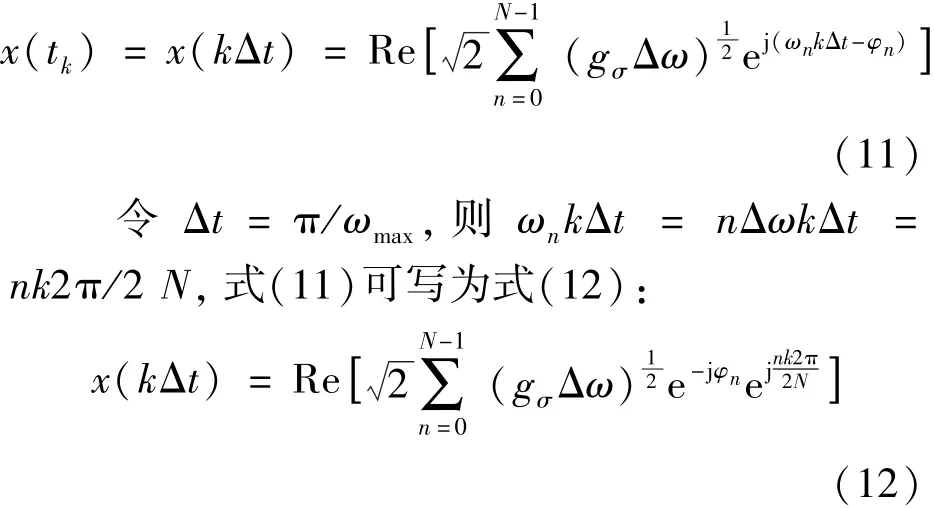
基于式（12）定义如式（13）所示序列：

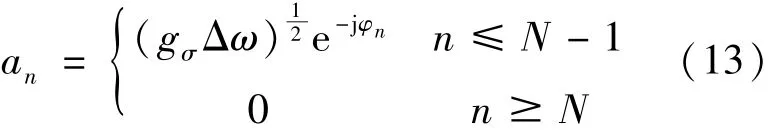
则x（tk）可通过快速傅里叶变换（FFT）得到，如式（14）：

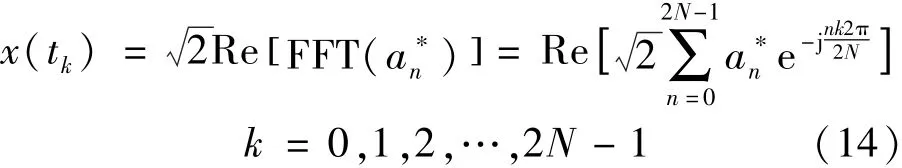
上式中，∗表示共轭，并利用到共轭复数实部相等的特性。

先根据式（9）计算各连续频带内的应力响应自谱，得到应力响应的自谱在全分析频带上的分布后，再通过式（14）获得其近似随机时间历程。

4 航天器实例分析

4.1 模型及分析流程

对某航天器发射段的中高频声振响应进行分析。该航天器由实验舱和资源舱组成，如图1所示，其中实验舱含密封舱，资源舱为非密封舱。航天器主体结构材料为铝合金（密度2640 kg／m3，弹性模量68 GPa，泊松比0.3），基本构件包括直梁、环形梁、平板、圆柱壳、圆锥壳、球壳等，基本构件与内部声腔以及整流罩内声场形成耦合声振系统。密封舱球底结构厚度为3 mm，球面直径为3.2 m，结构上有2个直径300 mm、厚度30 mm的铝合金法兰盘，见图2。

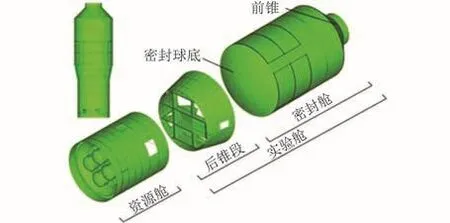
图1 某航天器舱段组成Fig.1 Module composition of a spacecraft

获取密封舱球底最大弯曲应力时程的分析流程如图3所示，最后采用羽流计数法对应力循环进行计数统计。雨流计数法是一种双参数计数方法［12］，可将载荷-时间历程简化为一系列的全循环，得到相应的载荷幅值和载荷循环次数。

利用VAone建立航天器统计能量模型，如图4所示。模型包含104个梁构件、202个板／壳构件及1个声腔，考虑所有构件中所有类型波场间的耦合，所有波场的内损耗因子均取值1%。资源舱后端与火箭连接，施加如图5所示的宽带随机激励，频率上限2 kHz。在所有暴露在整流罩内声场的板、壳构件表面施加如图6所示的噪声激励，假定结构壁面对声波刚性反射以考虑最恶劣工况，因此施加的噪声激励比图6所示条件大3 dB。在中心频率为31.5 Hz～8 kHz的9个倍频程上计算航天器的声振响应。

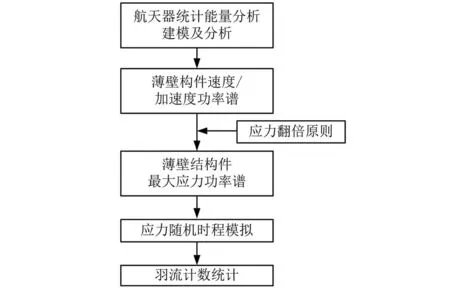
图3 最大应力分析流程Fig.3 Flowchat of maximum stress analysis

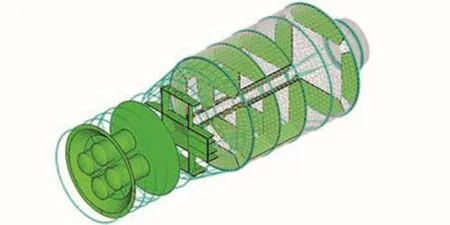
图4 航天器声振耦合模型（外壳结构未显示，网格区域表示内部声场）Fig.4 Vibro-acoustic model of the spacecraft（The outer structure is hidden，the meshed volume is inner acousitc acvity）

4.2 结果分析

图5 火箭对接面随机加速度载荷Fig.5 Acceleration load at the launch vehicle interface

图6 火箭整流罩内噪声载荷Fig.6 Acoustic load inside the launch vehicle fairing

位于航天器上、中和下部的密封舱前锥、球底及资源舱中段圆柱壳结构的厚度均为3 mm，这三种构件的弯曲均方根速度响应分别为0.08 m／s、0.11 m／s和0.14 m／s，可见随着距离火箭对接面的增大，构件均方根速度逐渐减小。图7显示了这三个构件弯曲均方根速度的谱分布，反映出各构件的响应能量主要分布在500 Hz以下，在较高频上由于主要受噪声激励影响且三种构件厚度相同，响应的谱分布相近。

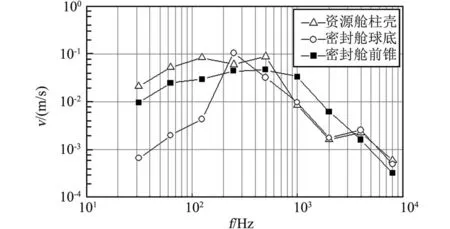
图7 航天器不同构件弯曲响应均方根速度Fig.7 RMS of flexural response velociy of structure components

对于密封舱球底结构，由于法兰盘相对球底薄壁厚度较大，对连接边界处的薄壁弯曲变形有较强的约束作用，因此两处法兰盘与球底薄壁连接处按刚性约束考虑以作保守估计，应力集中系数取4。根据密封球底弯曲波场能量计算得到的最大弯曲应力功率谱如图8所示，对比图8和图7可见，密封球底最大弯曲应力功率谱与其速度响应谱分布特点相似。

图8 密封舱球底最大弯曲应力功率谱Fig.8 PSD of maximum flexural stress at the spherical bottom

密封球底弯曲应力随机时程的一个模拟样本如图9所示，采样频率为22.4 kHz（为中心频率8 kHz倍频程上限频率的两倍），采样时间60 s。密封球底的应力随机时程包含大量转折，采用雨流计数法对其进行计数统计，得到不同幅值应力对应的循环次数见图10，由图可见，应力幅值在4～6 MPa的循环次数最多，应力幅值超过20 MPa的循环次数较少。不同的循环应力均值对应的循环次数见图11，由图可见，大部分应力循环的均值在0附近，随着应力均值的增大，对应的循环次数逐渐减小。

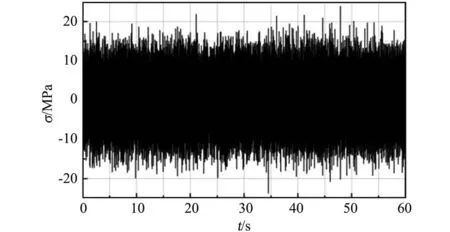
图9 密封舱球底应力随机时程样本Fig.9 Sample of random stress history at the spherical bottom

5 结论

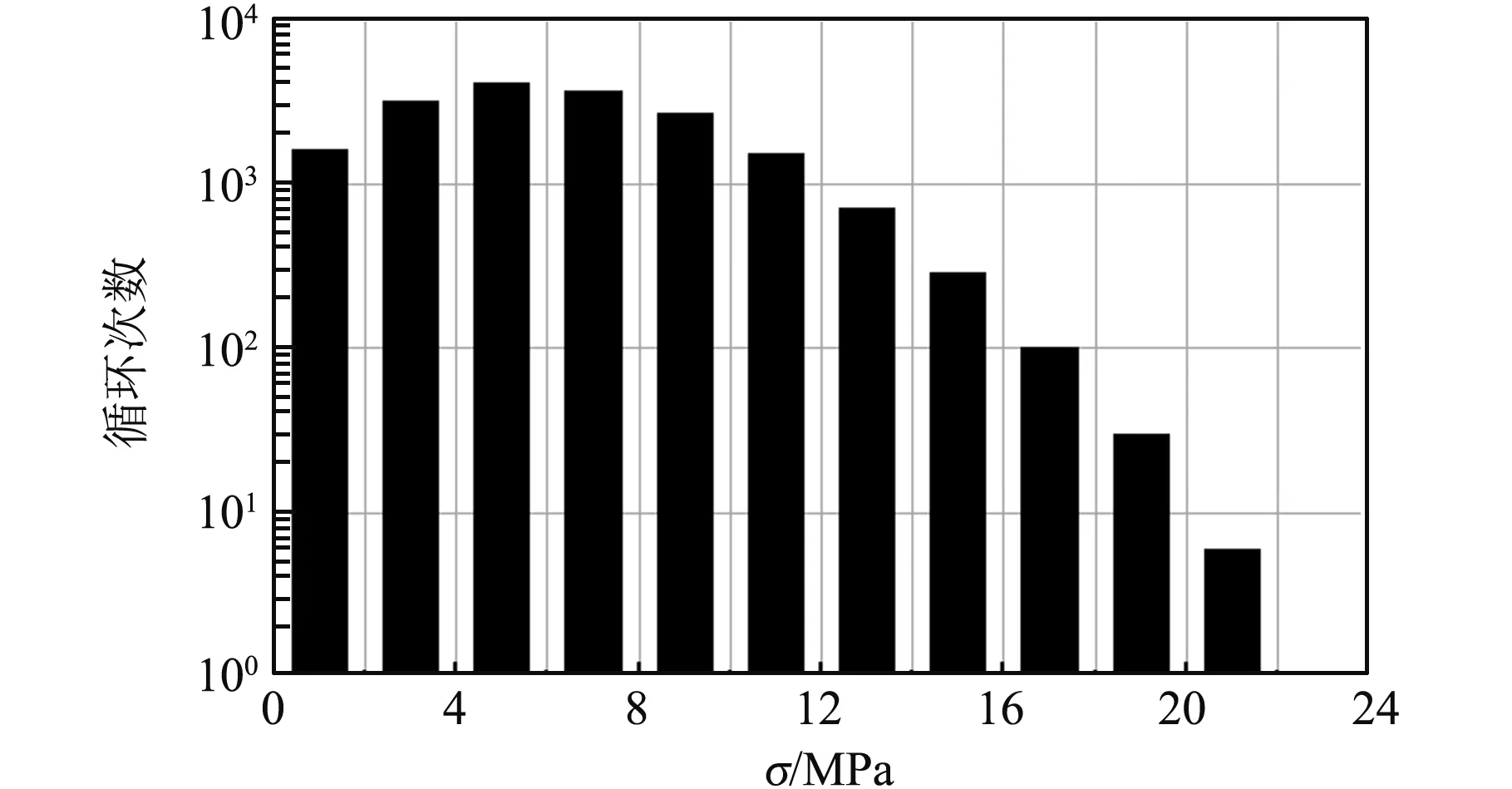
图10 应力循环幅值的雨流计数Fig.10 Rain-flow counting of amplitude of stress cycles

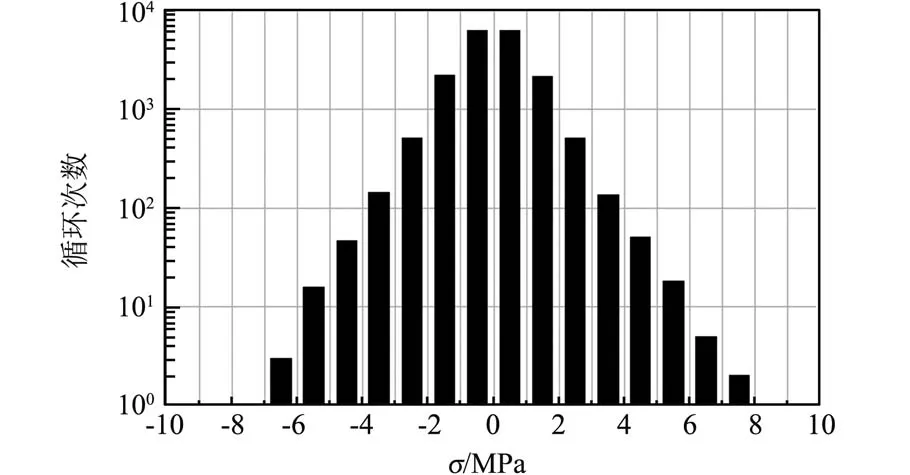
图11 应力循环均值的雨流计数Fig.11 Rain-flow counting of average of stress cycles

本文给出了一种航天器结构声振环境下应力时程分析方法，即先基于统计能量分析原理计算出薄壁构件空间平均的弯曲应力功率谱，然后基于应力翻倍原则获得薄壁构件上最大应力的功率谱，最后采用随机相位正弦波叠加的方式对最大应力的时间历程进行时域模拟。以某航天器的声振模型为分析实例，根据声振分析结果得到密封舱球底法兰盘附近最大弯曲应力的随机时程样本，并采用雨流计数法得到其计数统计结果。本文提供了一种分析声振环境下薄壁结构危险部位最大应力的时域方法，分析结果可为航天器薄壁结构的裂纹损伤评估提供依据。

（References）

［1］ JArenas J P， Margasahayam R N.Noise and vibration of spacecraft structures［J］.Ingeniare.Revista Chilena de Ingeniería， 2006， 14（3）： 251-264.

［2］ Dynamic Environmental Criteria［S］.NASA-HDBK-7005，2001.

［3］ Pai S S，Hoge P A，Patel B M，et al.Probabilistic estimation of critical flaw sizes in the primary structure welds of the Ares I-X launch vehicle ［R］.NASA／TM-2009-215583， 2009.

［4］ 张军，沙云东，倪绍华.基于功率谱密度的结构声疲劳寿命估算方法研究［J］.沈阳航空航天大学学报，2008，25（1）： 11-14.Zhang Jun， Sha Yundong， Ni Shaohua.A method study of structural sound fatigue life estimate on the basis of power spectral density［J］.Journal of ShenyangInstituteof Aeronautical Engineering， 2008， 25（1）： 11-14.（in Chinese）［5］ Marucchi-Chierro P C，Destefanis S.Integrated approach for the structural random vibration and the associated structural fatigue life prediction due to the launch acoustic load［C］／／AIAA／CIRA 13 th International Space Planes and Hypersonics Systems and Technologies， 2005： 1-9.

［6］ 游进，侯向阳，赖松柏，等.含裂纹载人密封舱体结构在轨失效分析方法［J］. 载人航天，2014，20（2）：110-115.You Jin， Hou Xiangyang， Lai Songbai， et al.Failure assessment method for habitable module structure containing cracks［J］.Manned Spaceflight， 2014， 20（2）： 110-115.（in Chinese）

［7］ 谢久林，杨松，张俊刚，等.航天器声振动力学环境响应分析［J］. 航天器环境工程，2006，23（2）：83-89.Xie Jiulin， Yang Song， Zhang Jungang， et al.The response prediction of the spacecraft under acoustic vibration environment［J］.Spacecraft Environment Engineering， 2006， 23（2）：83-89.（in Chinese）

［8］ Larko J M，Cotoni V.Vibroacoustic response of the NASA ACTS spacecraft antenna to launch acoustic excitation［R］.NASA／TM-2008-215168， 2008.

［9］ Richard H.Lyon，Richard G.DeJong.Theory and Application of Statistical Energy Analysis［M］.Boston：Butterworth-Heinemann，1995：209-221.

［10］ Shankar K.A study of dynamic stress concentration factors of a flat plate for SEA applications［J］.Journal of Sound and Vibration， 1998， 217（1）： 97-111.

［11］ Miles R N.Effect of spectral shape on acoustic fatigue life estimates［J］.Journal of Sound and Vibration， 1992， 153（2）：276-286.

［12］ ASTM E 1049-85 Standard Practices for Cycle Counting in Fatigue Analysis［S］.2005.

（责任编辑：龙晋伟）

Analysis of Time History of Stress on Spacecraft Structure in Vibro-acoustic Environment

YOU Jin， LAI Songbai， FANG Jie
（Institute of Manned Space System Engineering， China Academy of Space Technology， Beijing 100094， China）

V423.7

A

1674-5825（2017）05-0614-05

2016-12-19；

2017-08-14

国家重大科技专项（040103）

游进，男，博士，高级工程师，研究方向为载人航天器总体设计及结构动力学。E-mail：youjin1017＠hotmail.com