一种改进的基于TIN渐次加密的LiDAR点云滤波算法

岳桂昌，周玉娟

(河南省电力勘测设计院，河南 郑州 450000)

0 引 言

激光雷达技术（LiDAR）是一种全新的遥感技术，具有非接触、高精度和高效率等优点[1]。近年来，其相关技术的迅猛发展和日臻成熟，使其成为对地观测的一种新的更有力的手段，目前该技术已成功应用到城市测量、电力线勘测、森林管理、海岸线保护及地质灾害检测等多个领域[2]。

LiDAR数据包含了建筑物、植被、真实地面等全部的地形表面三维坐标，一般分为地面点和非地面点两类。在生成数字高程模型（DEM）前，必须剔除非地面点，即点云滤波[3]。滤波是LiDAR数据处理中的一个重要环节[4]，也是一项非常具有挑战性的工作，大约要耗费整个数据后续处理60%～80%的时间[5]。现有的点云滤波算法总体来说，主要分为形态学法、移动窗口法、基于地形坡度法、迭代线性最小二乘内插法等。

Lindenberger[6]最早提出了一维形态学的滤波算法，由于该算法是基于一维有序数据进行的，故局限性很大。Keqi Zhang[7]等人采用了变窗口大小的渐进形态学开运算对此方法进行了改进，提高了该算法的适用性，但其中的一些阈值参数是事先通过多组实验获得的经验值。Kilian[8]等人利用一个移动窗口，依据窗口大小赋予点一定权重，最后根据各个地面点权重插值生成DEM。Petzold et al[9]则采用逐步缩小窗口尺寸的方法渐次滤除非地面点。Vosselman[10]提出了一种类似于形态学运算的基于地形坡度的滤波方法，利用一个状如倒置漏斗或圆锥的操作元进行地面点滤除。Sithole[11]改进了该算法，采用圆锥形的操作元，利用局部最低点的边坡梯度来控制圆锥的倾斜角，以适应地形坡度的变化。迭代线性最小二乘内插法最早是由Kraus[12]提出的，其理论依据是最小二乘内插，数据点拟合后的高程残差不服从正态分布，比地面点高的地物点高程拟合残差为正值，且一般有较大偏差。

本文主要针对机载LiDAR点云数据的特点，根据Sohn提出的TIN滤波算法思想，提出了一种改进的TIN渐次加密滤波算法。

1 方法实现

1.1 原理概述

Sohn提出的TIN滤波算法[13]主要定义了两个关键的TIN加密过程：向下加密和向上加密。最终形成的TIN代表地形表面，其包含的点即为地形点；而没有包含在TIN内的点即为非地形点。

向下加密：这一步骤的目的是获取纯粹地形的初始表面模型。一个包含所有点云的矩形被确定，位于每个角点附近的点被假设为真实地形点。这四个角点按Delaunay准则进行三角剖分。然后，位于每个Delaunay三角形下的最低点被认为是地形点，并用于更新三角网。这个过程一直重复直至最后形成的三角网下面不存在任何点。这个最后形成的三角网即是假设的地形初始表面模型。重复此过程，直至没有新的被标记为“地形点”的点出现。该过程如图1所示。

图1 向下加密示意图Fig.1 Down-encryption schemes

向上加密：这一步骤的目的是改善向下加密完成的地形初始表面模型。在位于三角网内的每个三角形上面定义一个“缓冲区”,对于每一个三角形来说，位于缓冲区内的点被标记为“类地形点”；位于缓冲区以外的点则被标记为“非地形点”。被标记为“类地形点”的点是潜在的真实地形点，以这些点为顶点，分别建立四面体模型，如图2所示，利用能量公式（1），选择一个概率最大点，标记为“地形点”，加入到其对应的三角形中，更新TIN构网。

图2 四面体模型的建立Fig.2 The establishment of the tetrahedron model

式中，

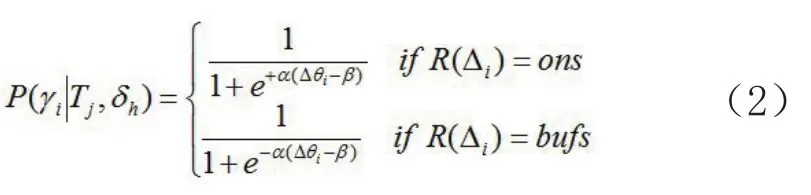
式（2）中，γions表示3个顶点均为地形点的三角形，即地形三角形；γibufs表示3个顶点中既有地形点，又有非地形点的三角形，即混合三角形；Tj表示第j个四面体模型；Tjin和Tjout分别表示模型的真值与粗差。图3给出了式中所涉及参数的直观表述。

图3 能量函数参数示意图Fig.3 Schematic energy function parameters

1.2 改进算法

1.2.1 初始面的构建

搜索位于超级矩形四顶点邻域内的种子点，并采用反距离加权平均为其赋值，这样就可以避免原始算法基于临近点均为地面点引入的误差。

将超级矩形顶点和筛选出的种子点采用逐点插入法进行TIN构网，并将得到的面作为初始面，如图4所示。先构建超级矩形，如图4(a)所示；然后建立规则格网，根据一定范围内高程最低点为地面点概率最大的原理，筛选种子点，如图4(b)所示；最后，利用种子点建立Delaunay三角网，如图4(c)所示。

图4 初始面的构成Fig.4 The establishment of the initial surface

1.2.2 基于局部地形坡度的自适应阈值

本文是在Microsoft Visual C++ 6.0平台上对原始算法进行重现的，在缓冲区阈值的选择上，原始算法忽略了地形的影响，直接取为固定值1，这往往会造成在某些复杂区域内，由于起初吸纳了一部分地物点，通过后续迭代过程而错误吸纳更多的地物点，即造成错误点的成片出现。本文考虑到阈值的大小往往与局部地形坡度密切相关，由此拟采用基于局部地形坡度的自适应阈值来替代原始算法中的固定阈值，以克服原始算法的不足。

1）局部地形坡度的计算

向下加密完成后，形成了一系列位于点云最下方的基准三角面，每一个三角面均可看作是一个局部地形面。由基面三角形的三个顶点坐标可得到基面的面方程：

本文是根据投影在该三角面内且距离在1m范围内的点来估算该面的局部坡度的。式（4）为投影点(x0,y0,z0)到基面的距离计算公式：

需要注意的一点是，这里的“投影”是指沿重力方向的投影，如图5所示。

图5 投影点示意图Fig.5 The projection point diagram

找到投影到该基面且到基面距离小于1 m的点后，遍历每个点，找到距离其最近的基面顶点，连线后求出其与基面的夹角θ，最后求出所有夹角的均值θ来估算地形局部坡度。夹角θ及θ的计算公式分别为式（5）和（6），图6为局部坡度示意图。

图6 地形局部坡度Fig.6 The local terrain gradient

2）筛选四面体顶点

当投影在该三角面内的点满足以下两个条件时，即选为四面体待选顶点。

条件一：点到三角面距离小于1 m；

条件二：点与三角面的夹角不大于 。

2 实验分析

2.1 实验数据

本文实验数据来源于网上公开的由Optech ALTM扫描仪获取的Vaihingen/Enz试验区和Stuttgart市中心的数据[14]，从中选取了两组具有不同典型地物特征的数据区,见表1。

表1 测区概况Tab.1 The general situation of the measurement area

2.2 实验结果与分析

在实验结果的定量评价上，本文采用的是George Sithole[5]提出的滤波误差，它将误差分为三类，即I类误差、II类误差、总误差，见表2

表2 误差统计Tab.2 Error statistics

表2中，a表示正确分类的地面点数目；b表示把地面点错分为非地面点的点数；c表示把非地面点错分为地面点的点数；d表示正确分类的非地面点数目。

表3为两个测区的误差统计对比表。

图7为两个测区的滤波效果对比图。

表3 滤波误差统计结果对比表Tab.3 The correlation table of the filtering error

图7 滤波效果对比图Fig.7 The correlation figure of the filtering error

由表3可以看出，改进算法较原始算法，三类误差均有所降低，I类误差降幅达50%，II类误差降幅达30%。从图7的测区滤波效果对比图来看，原始算法及改进算法，在地形比较平滑，地物高低起伏变化比较剧烈的区域，分类效果较理想；而在那些地形高低起伏较大，尤其是存在异常跳跃点（如陡坎、沟堑）的区域，识别效果不太理想。在桥梁与土壤无缝衔接的地方，两种算法均容易出现一些错归类的点，但改进算法效果还是有较大改变。在对一些低矮房屋的识别上，改进算法也更敏感，识别精确度更高

3 结束语

本文在深入研究原始TIN算法的基础上，从初始面构成及阈值选取上对原算法进行了改进。实验结果表明，与原算法相比，本文提出的改进算法可以有效降低三类误差，其中I类误差降幅达50%，II类误差降幅达30%，总误差降幅达40%。改进的算法可以更有效地滤除建筑物、植被、桥梁等地物点，具有较好的适用性与稳健性。不足之处是，算法滤波效果的评价是建立在测区数据事先进行人工分类标注前提下进行的，在实际情况中，还无法对滤波效果进行有效评判，所以探索有效的滤波评价体系是下一步需要努力的方向。同时，探索多源数据的智能化融合，结合额外数据源，进一步提高分类精度，也是值得进一步探索与研究的。