应用设计矩阵求解不同坐标系统转换下的参数问题
韩 笑,蒲英霞
(1. 南京大学 地理与海洋科学学院,江苏 南京 210023;2. 江苏省地理信息技术重点实验室,江苏 南京 210023;3. 江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023)
0 引 言
空间基准和坐标系统是大地测量、地图制图和“3S”技术中非常重要的组成部分,为了获取不同用途的地理空间数据,我们通常需要在不同空间基准(如北京1954、西安1980、WGS-84、CGCS2000等)和不同坐标系统(地理坐标、投影坐标、空间直角坐标等)之间相互转换[1]。如当采用GPS数据和地面控制点数据建立具有空间参考的卫星影像时,需要将GPS数据和地面控制点数据统一到相同的坐标系中;当合并不同数据来源的地图数据时,也需要先统一他们的空间参考系然后进行合并处理。
坐标变换是将空间数据从一个坐标系统转换到另一个坐标系统的过程,其实质是根据两个坐标系下的公共已知点求解坐标变换参数[2]。程新辉等人采用四参数法将北京1954转换至西安1980坐标系,并进行了转换误差的分析[3];王解先等人讨论了将WGS-84地心坐标转换到北京1954直角坐标的两个模型——平面转换模型和空间转换模型,并且比较了空间转换模型中三参数和七参数对模型转换结果的影响[4]。黎舒等研究了从西安1980到CGCS2000坐标系的变换方法,并根据具体情况提出了二维四参数、七参数和三维七参数等模型[5]。在坐标变换的误差处理方面,较为成熟且应用最广的是在求解参数的过程中采用最小二乘法[6]。孔建基于整体最小二乘法推导了四参数仿射变换的参数估计公式,避免了常规矩阵分解方法计算的复杂性[7];张鹏杰等提出利用加权整体最小二乘法进行参数求解,同时考虑原始坐标和目标坐标的误差,并根据误差的影响程度赋予不同的权值[8]。现有的坐标变换方法研究中,大多是基于给定的两个坐标系统来研究某一种坐标转换方法,往往是独立阐述,没有试图挖掘不同转换方法之间的联系。在利用最小二乘法推导参数估计表达式时,我们发现不同坐标变换方法的推导过程存在很大的相似性。本文在Allan研究的基础上[9],引入设计矩阵的概念,以此作为纽带将不同的坐标变换方法联系起来,推导出了基于最小二乘法的统一参数估计表达式。
1 不同坐标转换方法
在进行坐标变换的过程中,若已知两个不同坐标系统下足够数量的坐标点,即观测值个数大于必要观测数时,则可以采用最小二乘法求解坐标转换参数的最优估计值。一般地,根据一组已知数据集,利用最小二乘法解算未知参数的过程如下:
首先,建立已知坐标数据与未知坐标转换参数之间的一般函数关系式



在公式(1)中,当达到最优估计时,可得如下的微分关系式

将(3)式代入(4)式中,可以简化为

A,C是雅克比矩阵,在这里称之为设计矩阵[9]。
实际上,已知点的观测值总会因为量纲或者观测条件的不同而产生系统误差,为减小误差,我们在求解过程中计算残差平方的加权和,因而引入权矩阵W,可以推导出以下表达式:

式中,W是一个对角矩阵,且对角线元素对应着各自方差的倒数[9]。
基于公式(6)待求参数的一般表达式,问题的关键就变成求解不同坐标变换模型对应的设计矩阵。下面针对几个常用的坐标转换模型,给出设计矩阵的推导过程。
1.1 相似变换
对于二维坐标系下的相似变换,我们通常采用四参数模型,即经过坐标系的平移、旋转和比例变化实现[10-11]。该方法适用于坐标轴正交且各个方向的尺度因子相同的平面坐标系之间的转换,需要至少两个控制点来估计变换参数,具体表达如下:
设(Xs,Ys)表示源坐标系下的坐标值,(XT,YT)表示目标坐标系下的坐标值,则有函数关系式:

式中,a0、b0分别为X、Y方向的平移参数,a=μcosα,b=μsinα,α为旋转角度,μ为两坐标轴的尺度参数。
设计矩阵A,C可以表示为:

进一步解算出:

以上的演算过程是针对单一坐标点的。通常情况下,会提供多个已知点的坐标值,这时我们可以用Ai,Ci来表示第i个点的设计矩阵,将所有已知点的设计矩阵组合在一起,可得表达式:

1.2 仿射变换
仿射变换是基于仿射坐标系而建立的一种坐标变换数学模型,是经过坐标系的平移、比例、旋转、对称和错切等复合变换得到的[12]。仿射变换适用于坐标轴不正交或者各个方向尺度因子不同的参考系,要求至少3个控制点来求解变换参数,其基本关系式为:

式中,a0、b0分别为X、Y方向的平移参数,a1=μxcosα,b1=μxsinα;a2=μysinα ,b2=μycosα,α为旋转角度,μx、μy分别为X、Y轴的尺度参数。特别地,当 μx=μy时,有a1=b2,a2=b1,此时的六参数仿射变换关系式与四参数相似变换相同,即四参数相似变换是六参数仿射变换的特殊形式。
第i个点的设计矩阵Ai,Ci:
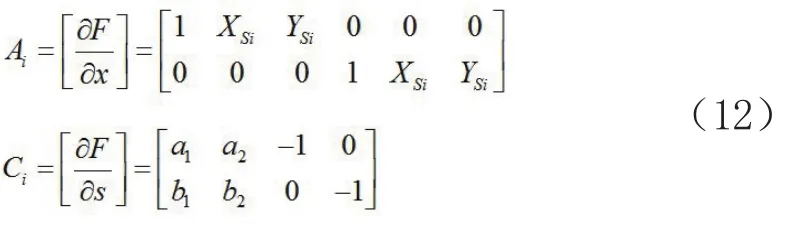
将所有已知点的设计矩阵组合在一起:
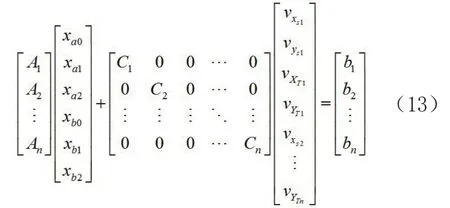
1.3 七参数相似变换法
三维地心参考系下的坐标变换,通常采用七参数变换模型[13],即3个平移量、3个旋转角和1个尺度因子,该变换需要至少3个以上的控制点,其模型表达式为:

式中,ΔX、ΔY、ΔZ分别为XS、YS、ZS方向的偏移量,R为旋转矩阵,αx、αy、αz分别为XS、YS、ZS坐标轴的旋转角。
一般地,比例因子接近于1,所以我们可以用(1+κ)表示比例因子,κ为极小量。第i个点的设计矩阵为:

这种转换方法最普遍的应用是一个大地基准向另一个大地基准的转化,这些情况下旋转角都非常小(几乎只是几秒),因此,XS>> YS,则有:

同理,

将以上代入(16)、(18)式中,有:

闭合差向量:

将所有已知点的设计矩阵组合在一起,有:

2 算例验证
本文选取了某地5个控制点分别在北京1954和西安1980坐标系统下的坐标值,采用二维坐标系统下的四参数相似变换和六参数仿射变换模型,推导设计矩阵,求解变换参数。表1给出了上述5个控制点分别在两个不同坐标系统下的高斯平面直角坐标值。
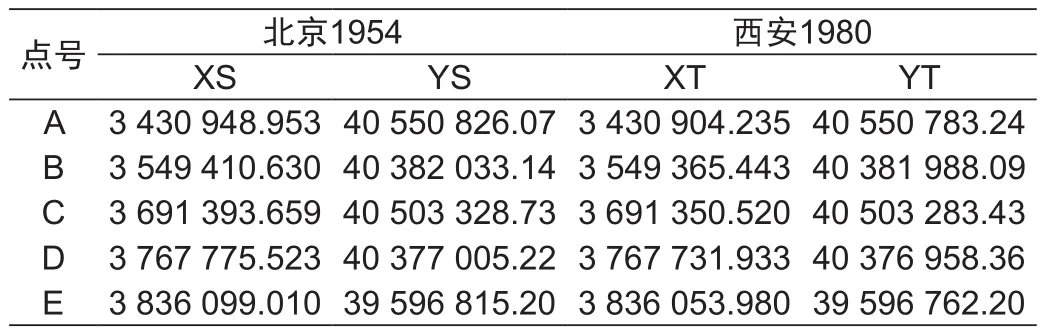
表1 控制点在北京1954和西安1980坐标系下的坐标值Tab.1 Coordinates of control points in Beijing 1954 and Xi'an 1980
应用公式(8),可以计算出相似变换下的设计矩阵A、C,代入公式(6)求得相似变换参数:a0=-229.386 7,b0=-366.942 8,a=1.000 008 3,b=0.000003 84。
同理,应用公式(12),求出仿射变换下的设计矩阵A和C,代入公式(6)求得变换参数:a0=-200.398 66,a1=1.000 006 24,a2=0.000 003 306,b0=-303.194 67,b1=-0.000 008 182,b2=1.000 007 11。
选取CGCS2000和西安1980坐标系下的F、G、H、I 4个控制点坐标,需要将CGCS000的大地坐标和西安1980的高斯平面坐标转化到空间直角坐标系中(见表2),然后采用三维坐标系下的七参数变换模型,推导出设计矩阵,求解变换参数。

表2 控制点在CGCS2000和西安1980下的坐标值Tab.2 Coordinates of control points in CGCS2000 and Xi'an 1980
根据公式(19)、(20),列出七参数变换的设计矩阵A和C,由公式(6)计算得到相应的变换参数:k=-2.219E-06,αx=-9.506 7E-07,αy=9.218E-06,αz=-1.295E-05,ΔX=190.248,ΔY=103.828,ΔZ=30.551 6。
接下来,将3种变换方法计算得到的变换参数应用到该区域内的11个控制点,分别计算这些点在北京1954转西安1980的相似变换、北京1954转西安1980的仿射变换、CGCS2000转西安1980的七参数相似变换下的坐标值,比较计算值与真实值的差异(表3,表4,表5)。相似变化的X、Y均方根误差分别为0.1353和0.1755,仿射变化的X、Y均方根误差分别为0.1407和0.0127,七参数相似变化的X、Y、h上的均方根误差分别为0.0033、0.0022和0.5178,均在可接受范围内。比较相似变换和仿射变换的均方根误差可以看出,相似变换与仿射变换在X方向的均方根误差比较接近,但在Y方向的均方根误差相差较大。如我们所知,假设坐标轴正交,且各个方向的尺度因子相同,则仿射变换的表达式与相似变换相同,即a1=b2=a,a2=-b1=b。回顾上面参数估计的结果发现,a1、b2的估计值与a的估计值相近,a2的估计值与b的估计值也较为接近,但-b1的值与b的值相差较大,因此,相似变换与仿射变换在Y坐标的计算上差异较大。不同于前面两者,七参数相似变换是适用于三维直角坐标系的,其考虑的参数更加充分,因此,在X、Y方向的误差值相对较小,计算结果更接近真实值。
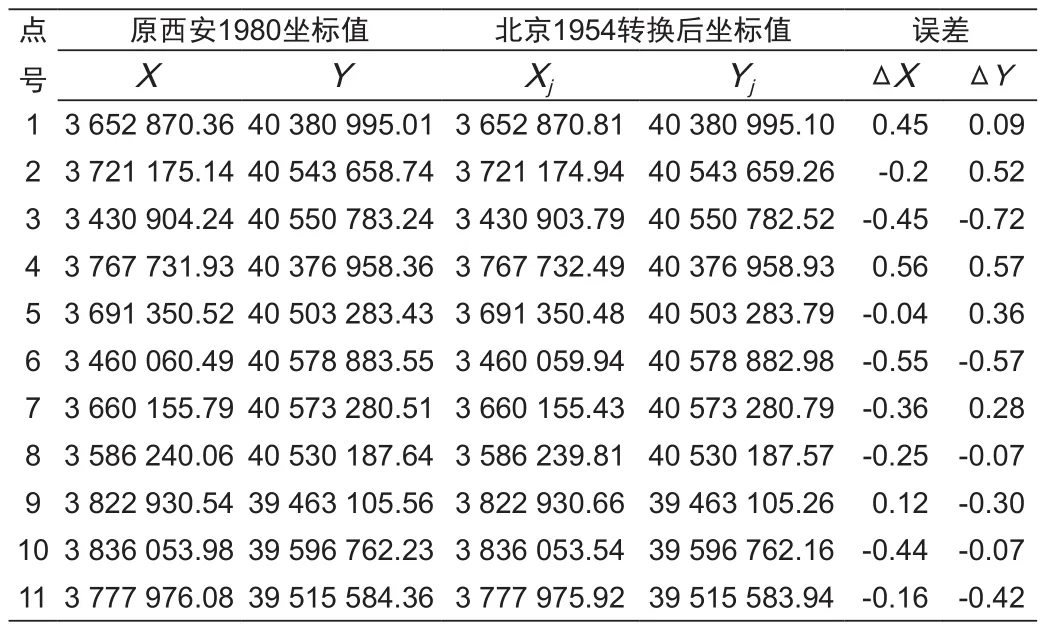
表3 相似变换的计算值和真值比较Tab.3 Comparison between calculated values and true values in similarity transformation

表4 仿射变换计算值与真值比较Tab.4 Comparison between calculated values and true values in aきne transformation
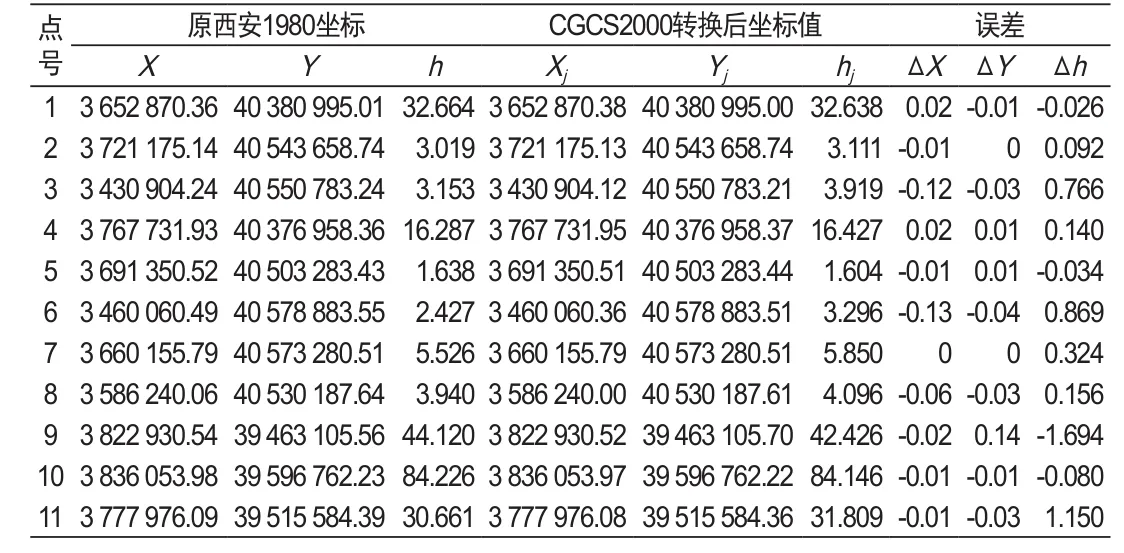
表5 七参数相似变换计算值与真值比较Tab.5 Comparison between calculated values and true values in sevenparameter similarity transformation
3 结束语
本文在常用坐标转换模型研究的基础上,引用设计矩阵的概念,根据最小二乘法原理推导了坐标变换统一的参数估计表达式。以四参数相似变换、六参数仿射变换和三维七参数相似变换为例,分别阐述了应用设计矩阵求解变换参数的过程,并将求得的参数应用于其他控制点,比较计算值与真实值的误差,有效验证了引用设计矩阵的合理性。与前人的工作相比,本文的特点在于以设计矩阵为纽带,将不同的坐标变换方法联系起来,对于给定的坐标变换方法,只要求出其设计矩阵,代入参数估计表达式进行求解,简化了计算过程。需要注意的是,在进行坐标变换时应该根据点的分布情况,合理地选择控制点。在满足控制点合理分布的条件下,控制点个数越多,计算结果往往更加精确。特别地,自2008年启用CGCS2000坐标系以来,随着国家经济建设的发展,地方坐标系测绘成果向CGCS2000转换的需求越来越大,本文的研究有助于提高地理坐标系转换的效率,推广CGCS2000坐标系的使用。

