基于GIS的宁波市道路网络综合通达性研究

史滢宜，刘艳芳＊，银超慧

(1.武汉大学 资源与环境科学学院，湖北 武汉 430079；2.武汉大学 教育部地理信息系统重点实验室，湖北 武汉 430079)

0 引 言

交通网络作为交通运输系统的重要组成部分，是承载人类活动的基本构件之一[1]。城市交通网络不仅是城市繁荣、有序和高速发展的主要支撑条件，也一定程度上决定了城市居民的生活方式，发挥着至关重要的作用。加速的城市化进程对改善和优化城市交通网络的布局提出了新的挑战。交通网络通达性可以为城市交通网络的规划建设和运输组织提供科学的理论依据，对进一步提高城市综合竞争力和区域影响力、促进城市的可持续发展具有重要意义[2]。

1959年Hansen[3]首先提出通达性的概念，将其定义为交通网络中各节点相互作用机会的大小。简单地说，通达性即为一个地方到达另一个地方的容易程度[4]。通达性广泛用于土地利用开发、城市总体规划、交通规划以及旅游资源开发等各个领域，成为国内外学者的研究热点。国外学者对交通通达性的研究起步较早，如20世纪70年代Zakaria[5]对费城公共交通通达性与土地利用增长率之间的关系进行了分析，认为通达性对土地利用的影响具有区域差异；Murayama Y[6]研究了日本铁路发展对国内城市体系通达性的影响；Gutierrez[7]和Vickerman[8]分别选择了不同的通达性评价方法证实欧洲高速铁路网的兴建有利于提高边缘区的通达性水平；sullivan[9]基于GIS技术，采用传统重力公式和时间地理的研究框架分析了公共交通的通达性；Michael[10]等以美国俄亥俄州辛辛那提市为例，强调了公共交通系统中超市通达性的重要性。

国内有关交通通达性的应用性研究开始于21世纪，研究内容可以分为3个方面：①对通达性的评价方法及其空间格局的研究，如金凤君和王娇娥[11]总结了20世纪中国铁路交通网络的结构演化以及由此引起的通达性空间格局的变化；刘承良等[12]以武汉都市圈为例，通过距离算法、拓扑算法和空间句法模型定量分析路网空间通达性；陈少沛等[13]基于GIS技术对广州市轨道交通网络通达性进行度量和空间特征分析；②对通达性的时空格局及其演化特征的研究，如刘承良等[14]计量揭示了1989～2010年武汉城市圈道路网通达性的空间演化规律；段德忠等[15]以荆州市112个乡镇为例，基于城市腹地范围建立乡镇通达性评价体系，研究2000～2011年荆州市乡镇通达性的时空演化格局；梅志雄等[16]等采用空间句法模型与GIS结合的方法，定量分析1990年以来珠三角公路网通达性时空演变，证实珠三角公路通达性与城市潜力呈正相关性并得到增强；③通达性与土地利用、区域经济、城市扩张等方面的研究，体现出城市交通网络是城市发展的载体。李志等[17]将南京市地铁通达性格局变化与地价格局变化进行空间耦合对比，探讨不同类型用地对地铁通达性的增值响应模式；李涛等[18]认为1990年以来珠江三角洲地区交通网络通达性与人口变化的关系逐步增强；周恺[19]探讨了长江三角洲地区高速公路网通达性和区域城镇体系空间结构之间的关系。

综上所述，国外的通达性理论和应用研究发展较早，更为成熟；国内通达性的研究趋势从理论到应用，从国家尺度到区域尺度，从单指标到多指标评价，呈现出多方法、多尺度、多时间段的特征，但是在城市尺度上对于道路密集的建成区范围内的交通通达性研究相对较少，且现有单个城市的通达性研究中几乎没有考虑到公共交通在城市交通通达性中的重要作用。本文以宁波市中心城区道路网络和公交网络为对象，选择距离度量模型、道路加权核密度模型、路网连通度和公交服务指数构建综合通达性，分析宁波市中心城区综合通达性的空间特征，对未来宁波市城市交通网络的建设和扩张具有借鉴意义。

1 研究区与数据准备

1.1 研究区

宁波市位于东经120°55'～122°16'，北纬28°51'至30°33'。地处我国海岸线中段，长江三角洲南翼。东有舟山群岛为天然屏障，北濒杭州湾，西接绍兴市的嵊州、新昌、上虞，南临三门湾，并与台州的三门、天台相连。宁波市辖海曙、江东、江北、镇海、北仑、鄞州6个区，宁海、象山2个县，慈溪、余姚、奉化3个县级市。全市陆域总面积9816 km2，其中市区面积为2462 km2。

本文界定宁波市的中心城区为研究范围，包括江东区、海曙区以及江北区、北仑区、镇海区、鄞州区的部分地区，区域面积708.49 km2，为城市道路网络密集分布区域，因此具有研究城市道路网络的代表性（如图1所示）。

1.2 数据获取与处理

1.2.1 基础数据

以宁波市交通地图册为基础，运用ArcGIS10.2软件，建立宁波市中心城区路网空间数据库，城市道路总里程为2305.15 km，其中快速路59.14 km，主干路853.97 km，次干路776.59 km，支路615.45 km。至2014年年底，宁波市中心城区共通过公交（常规公交）线路353条，公交站点15 057个，如图2所示。

图1 宁波市中心城区道路分布Fig.1 Road map of Ningbo city center

图2 宁波市中心城区公交线网分布Fig.2 Map of Ningbo downtown pubic traきc network

1.2.2 行车速度

行车速度根据中华人民共和国城市道路工程设计规范（CJJ37-2012）、宁波市城乡规划管理技术规定（2014年）以及訾琨等[20]相关研究而定，见表1。

表1 不同等级城市道路行车速度表Tab.1 Traきc speed for diあerent classes of urban road

1.2.3 权重分配

李乐乐等[21]人认为，不同等级道路的权重可简单看作道路车道数的比值，参考其对西安市交通网络通达性的研究，在构建道路加权核密度模型时，将不同等级城市道路的权重分配见表2。

表2 不同等级城市道路权重表Tab.2 Weight for diあerent classes of urban road

2 研究方法

以距离度量模型、道路加权核密度模型、路网连通度和公交服务指数为基础，构建综合通达度评价指标，分析宁波市中心城区的路网通达性。

2.1 距离度量模型

道路节点之间的运输距离是衡量节点间可达程度的重要指标[22]。由于研究区域尺度较小，相交道路为四条及以上的路口视为重要交通路口，将满足该条件的1390个路口点作为空间节点，利用距离模型对空间距离和时间距离两个方面进行通达性度量，距离越短，节点的通达性越高。时间为路径长度与行车速度的比值，其中行车速度的确定具体见表1。该模型通过ArcGIS10.2的网络分析功能实现。

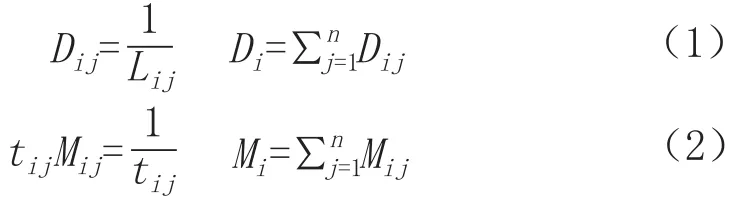
式中，Lij和tij分别为节点i到节点j之间的最短空间距离和最短时间距离；为方便结果分析对比，将Lij和tij分别取倒数，即Dij表示节点i到节点j的空间可达性；Mij是节点i到节点j的时间可达性；Di和Mi为节点i的空间距离通达性和时间距离通达性，其值越大，则该节点的通达性越好。

2.2 道路加权核密度模型

道路密度是衡量城市道路建设水平的重要指标。核密度估计(Kernel Density Estimation，简称KDE)[23]是借助一个移动的单元格，利用核函数来计算单元格内要素的密度估计方法，其本质是通过加权平均中心点位于采样值的局部函数来估计未知的密度分布[24]，通过该方法获得的连续表面能够表现出区域内各类型要素的密度分布特征。刘锐[25]、刘建军[26]等学者近年来将该计量方法引入到道路网络的分析中，本文借鉴前人的研究构建道路加权核密度模型，并考虑到不同等级道路的不同影响，将各等级道路进行加权处理。假设x1、x2…xn是具体的样本值，获得某点x处的密度值f(x)，采用Rosenblatt-Parzen核密度估计法，具体公式如下：

式中，n为样本数，xi为独立样本，x-xi为估计点到样本点xi的距离，h为带宽，为核函数。其中h数值的大小直接影响着分析结果，ArcGIS中将自动生成默认的h值，该默认值为输出空间参考中输出范围的宽度或高度的最小值除以30得到。本文结合自动生成的默认值，对不同的h值进行试验，选定最佳参数1000。不同等级道路的权重见表2。

2.3 路网连通度

路网连通度定义为区域内各节点之间依靠道路相互连通的强度，能够从道路网络布局方面反映路网的结构特点[27]。计算公式[28]为：

式中，C为研究区域内道路网连通度；L表示研究区域内道路总里程(km)；A表示区域面积(km2)；N为研究区域内应连接的节点数，ξ为区域内道路网络的变形系数，也称非直线系数，其含义为实际线路总里程与直线总里程的比值。这项指标通常用于大范围区域的道路网络分析，由于本文只对中心城区道路网络进行研究，各节点为城市道路交点，因此视为理想状态，变形系数ξ等于1。

当C值近似1.0时，路网布局为树状，路网连通性较差；当C值为2.0时，路网布局为方格网状，路网连通性较好；当C值大于3.0时，路网布局为三角网状，路网连通性更好，路网更为完善。汽车专用公路网的C值介于1.6～2.0之间表示成熟状态(或基本完善)，干线公路网达到2.5以上表示成熟状态，不同层次路网要求的性能及结点选取条件不同[29]。

2.4 公交服务指数

城市公共交通系统作为人们日常出行的主要方式，是城市道路交通的重要组成部分，是联系国民生活、社会生产和流通领域的关键环节。本文以城市公共客运交通（常规公交）网络为研究对象。在前人对城市交通网络通达性的研究[21]中，提出了“道路服务指数”的概念，以距道路一定距离的缓冲区作为道路所能服务的区域，计算此区域所占的面积占区域总面积的比重。考虑到城市公共交通在城市交通网络中担当了重要角色，本文提出“公交服务指数”这一概念，将其定义为距公交站点一定范围内的房屋建筑（区）面积占城市房屋建筑（区）总面积的百分比，可以反映城市居民接近公共交通的程度，而公交站点作为人们出行换乘的枢纽，其分布的合理性将直接影响公交线路网的通达水平。根据有关公交站点服务面积的文献研究[29-32]以及城市道路交通规划设计规范（GB50220-95），确定300m为服务半径。

式中，n为公交站点的数量；Si为公交站点的服务面积；A为房屋建筑（区）面积；F为公交服务指数，F越大，表明区域公交网络的通达性越好。

3 结果与分析

3.1 距离度量模型

3.1.1 最短空间距离

在所研究的1 390个节点中，基于最短空间距离倒数的通达性最优节点位于江东区江东北路与百丈路交叉口，与宁波市市中心的地理位置相接近。通达性最差节点位于新一路与横江路交叉口附近，为北仑区的最东端。前90个通达性最优节点均位于江东区和海曙区，后50个最差节点除2个位于镇海区以外，其余均分布在北仑区。

如图3所示，通过对节点空间距离通达性进行克里金插值分析，宁波市的空间距离通达性在空间上具有双中心结构，均呈现同心环状态，其中位于海曙区和江东区的中心影响范围较大，逐渐向周围递减，其辐射范围包括鄞州区、镇海区和江北区。位于北仑区中心的空间通达性影响范围较小，其强度不及宁波市市中心，同样呈现由区中心向周围递减的分布状态，但是辐射范围仅限于北仑区内。

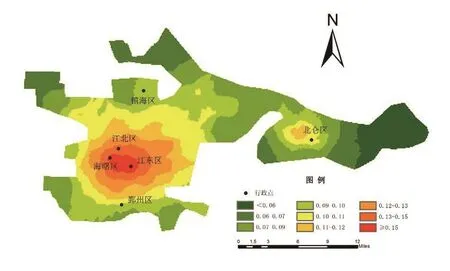
图3 宁波市空间距离通达性插值分布Fig.3 Map of Ningbo spatial distance accessibility interpolation

3.1.2 最短时间距离

基于最短时间距离倒数的通达性最优节点位于江东区甬港北路和宁穿路的交叉口，这与市中心的地理位置稍有偏差，时间距离通达性不仅依靠区域中心性，也与道路的路宽和通行速度相关；通达性最差节点同样出现在北仑区的最东端。前50个时间距离通达性最优的节点分布在江东区、海曙区和鄞州区，后50个最差节点除6个位于镇海区以外，其余均分布在北仑区。

在空间格局上，与空间距离通达性的分布相比，位于海曙区和江东区的中心范围向东北方向扩充至镇海区的南部和鄞州区的东北部。江北区开元路与长兴路交叉口呈现出较优的时间距离通达性，此处附近区域成为高值的聚集区。北仑区的时间距离通达性仍为独立的空间格局，出现双中心圈层结构，以南海路、钱塘江中路与黄山西路的交叉路口地带为第一中心，北仑区政府附近为第二中心。

3.2 道路加权核密度模型

宁波市中心城区交通网络中，道路加权核密度值最高的区域主要集中在海曙区和江东区的政府所在地之间，形成带状分布。该处位于三江交汇处，天一广场、鼓楼和城隍庙等在该处周边分布，为宁波市的中心商业区。此外，高密度地区还包括北仑区政府一带，作为距离市中心最远的市辖区，北仑区拥有不同于其他区的发展模式，借助北仑港的优势和工业发展，其道路交通的发达也反映出北仑区的经济实力。道路加权核密度值较低的区域主要分布在中心城区区划的边界地带，以郊野、风景区为主，城市道路较少或没有建立，如图4所示。

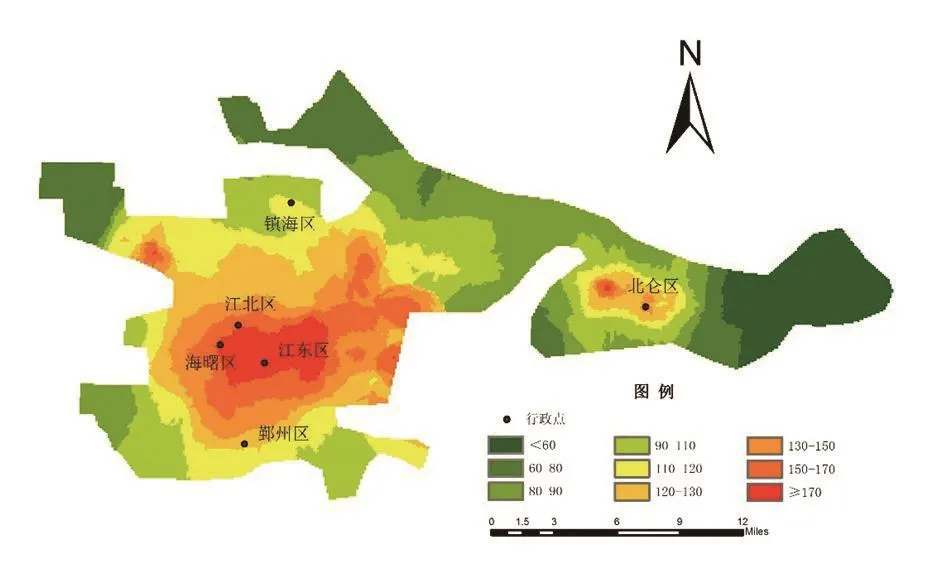
图4 宁波市时间距离通达性插值分布Fig.4 Map of Ningbo temporal distance accessibility interpolation

从空间结构上来看，宁波市中心城区道路加权核密度呈现以市中心三江口地带为中心度圈层分布状态，北仑区成为仅次该区域的高值分布地区，如图5所示。

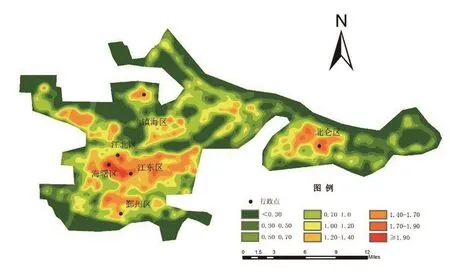
图5 宁波市道路加权核密度分布Fig.5 Map of Ningbo road network weighted kernel density

3.3 路网连通度

宁波市整体路网连通度C为1.33，各区的路网连通度均大于1，表明宁波市中心城区道路网络整体接近方格网状，连通情况较好。各区中江东区的路网连通度最高，为1.74，其次为海曙区和北仑区，分别达到1.49和1.34，均高出宁波市整体水平。江东区是宁波市重点建设的核心城区和重点区，沪杭甬高速公路和沿海大通道在区内交会，是中心城区通往北仑港、宁波经济技术开发区、保税区、大榭开发区的主要通道。作为枢纽性区域和未来的行政服务中心，江东区的交通地位不容小觑。

鄞州区的路网连通度与整体水平相当，而镇海区和江北区分别为1.30和1.24，略低于宁波市整体水平。江北区的路网连通度最低，主要由于其辖内庄桥街道的北部和甬江街道的中部地区以村庄为主，几乎无城市道路分布，影响整个区的道路连通状态。

从路网的连通度空间格局上来看，宁波市中心城区的路网连通度呈现中部最高，东南高于西北的变化趋势，如图6所示。

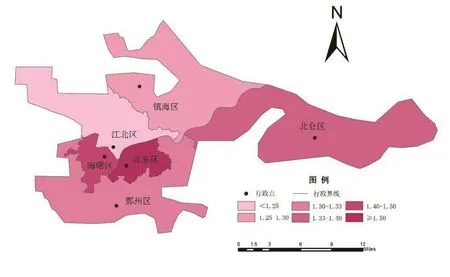
图6 宁波市路网连通度分布Fig.6 Map of Ningbo road network connectivity

3.4 公交服务指数

宁波市公交服务指数为24.61%，代表了中心城区的整体水平。各区中江东区和海曙区的公交服务指数远高于其他地区，均超出整体水平，分别为58.35%和57.61%，表明这两个区距公交站点300 m以内的房屋建筑（区）面积超出区域房屋建筑（区）面积的一半。江东区和海曙区均为宁波市区的中心区域，公交线网全面覆盖并向外辐射到其他地区，且两区的房屋建筑（区）面积均占区域总面积的65%左右，因此公交服务指数位居前列。

鄞州区和江北区的公交服务指数接近中心城区的整体水平，分别为26.4%和26.24%。而北仑区和镇海区低于整体水平，分别为18.37%和16.97%。北仑区和镇海区的公交线路和站点数相对其他区较少，且部分房屋建筑（区）的分布距离公交站点较远。

从公交服务指数的空间格局上看，宁波市中心城区的公交服务指数呈现西南高，东北部较低的空间布局，如图7所示。

图7 宁波市公交服务指数分布Fig.7 Map of Ningbo public transport service index

3.5 综合通达性

距离度量模型、道路加权核密度、路网连通度和公交服务指数分别从路网的连接结构、路网密度、路网发育程度、公交便捷性等不同方面反映了宁波市城市道路网络的通达性。然而单一模型并不能充分反映路网通达性的整体格局，为了综合描述宁波市路网通达性的整体空间格局，本文采用计算综合分值的方法进行分析。首先对各项指标进行0～100的线性标准化，使指标之间具有可比性；然后将各指标值等权相加，得到综合通达性指数值，其值越高，表明该区域通达性水平越高，反之则越低。

运用SPSS将各项模型指标值与综合通达性进行相关性分析，结果显示公交服务指数与综合通达性的相关性最高，相关度为0.988（在0.01水平上），表明公交服务指数对综合通达性具有显著影响。公共交通的便捷程度对于提高城市道路网络通达性意义重大。

宁波市综合通达性在空间上呈现出西南高东北低的整体格局，综合通达性指数值由大到小排列依次为江东区、海曙区、鄞州区、江北区、北仑区和镇海区。综合通达性从市中心向东北方向产生递减趋势，北仑区虽然距离较远，但是具有较为完善的路网布局和结构，镇海区成为综合通达性最差的区域，如图8所示。

图8 宁波市道路网络综合通达性分布Fig.8 Map of Ningbo road network comprehensive accessibility

4 结束语

本文以距离度量模型、道路加权核密度、路网连通度和公交服务指数为基础，构建综合评价指标，分析了宁波市中心城区道路网络的通达性及其空间特征。整体来说，宁波市城市道路网络发育良好，路网建设基本完善，其通达性空间格局呈现出以江东区为首，西南高、东北低的分布状态。

道路加权核密度和路网连通度主要反映路网的发育程度，距离度量模型和公交服务指数更多的是反映路网的布局状态。宁波市最短空间距离和最短时间距离指数值最高的均为江东区，空间格局较为相似；道路加权核密度最高值为海曙区，其空间结构呈大小双中心分布，较大中心区的辐射范围较广，包括海曙区、江东区等五区，较小中心区以北仑区为范围，较为独立；路网连通度指数值最高为江东区，最低为江北区；公交服务指数以江东区和海曙区最高，其空间格局分布与综合通达性最为相似。

江东区和海曙区作为中心商业区，道路体系基本成熟，交通优势较为突出，综合通达程度最优；鄞州区和江北区具有较为完善的道路体系，综合通达程度次之；北仑区虽然具有较为良好的道路结构网络，但是和镇海区受地理区位等因素的影响，综合通达性较差。应从整体布局出发，进一步加强除中心商业区以外的区域道路交通网络建设，促进各区之间相互联系，有效进行交通分流，完善城市道路体系。

对各指标与综合通达性进行相关性分析，结果显示公交服务指数与综合通达性的相关度最高，其次分别为最短空间距离和最短时间距离。宁波市道路网络空间布局对综合通达性产生的影响更为显著，这可能是中心城区东西跨度较大的缘故，而道路结构的影响不及空间布局。

本文以GIS为技术支撑，探讨了宁波市中心城区道路网络通达性及其空间特征，但只是在静态层面方面进行分析，缺乏动态层面（时间尺度）的研究。由于轨道交通线路较少，没有考虑其对宁波市通达性的影响。另外，区域交通网络综合通达性需要考虑更多因素，如费用因素和人的因素，在此文中未提及。可以在这些方面做进一步的研究，考虑用户出行动机、路径选择等，综合评价路网通达性，促进城市道路体系合理化建设。