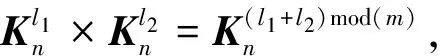图的两类运算性质
张倩男,陈金阳
(湖北师范大学 数学与统计学院,湖北 黄石 435002)
图的两类运算性质
张倩男,陈金阳
(湖北师范大学 数学与统计学院,湖北 黄石 435002)
在图论研究中,图的运算是构造具有特殊性质的图的一种方法.文本对图G的两类运算从结构、运算规律、性质等方面进行研究,进而将其作用在完全图Kn上,构造出与剩余类加群同构的有限群。
完全图;模n剩余类群;同构
1 问题背景
在图论研究中,图的运算是构造具有特殊性质图的一种方法,这种运算作用在特殊图上有可能构成代数系统,乃至构成群.在代数研究中,群论占有重要地位,用群理论构造特殊性质的图也是图论研究的一个重要方法,如Cayley图,Bi-Cayley图都是通过群构造的,它们均具有较好的图论性质,如正则性,连通性,哈密尔顿性等.有关这方面理论研究参看文献[1~3].
本文首先研究了图的两种特殊运算G1*G2和G1×G2的运算性质,进而将其作用在完全图Kn上,构造出与剩余类加群同构的有限群.
2 基本概念及术语
定义1 “*”运算:令H1=G1*G2,则
1)V(H1)=V(G1)∪V(G2);

注:“*”运算可以提高图的连通性,设|V(G1)|=n1,|V(G2)|=n2则:
∀vi∈V(G1),dH1(vi)=dG1(vi)+n2∀vj∈V(G2),dH1(vj)=dG2(vj)+n1
每个顶点的度都增大了,进而提高了图的连通性.
定义2 “*”运算: 令H2=G1×G2,则
2) 任意两点(x1,y1),(x2,y2)∈V(H2)在H2中邻接当且仅当以下条件之一成立:
Ⅰ)x1=x2且y1~y2inG2;
Ⅱ)y1=y2且x1~x2inG1.
定义3 图同构: 对图G1,G2,若存在一个双射φ∶V(G1)→V(G2), 使
xy∈E(G1) ⟺φ(x)φ(y)∈E(G2)
称G1与G2同构,记作G1≅G2.
3 两种运算的一般性质
定理1 “*”运算满足下面两条性质:
1) 结合律:(G1*G2)*G3=G1*(G2*G3);
2) 交换律:G1*G2=G2*G1.
证明: 1)由定义知,
V((G1*G2)*G3)=V(G1*G2)∪V(G3)=(V(G1)∪V(G2))∪V(G3)=
V(G1)∪(V(G2)∪V(G3))=V(G1)∪V(G2*G3)=
V(G1*(G2*G3))
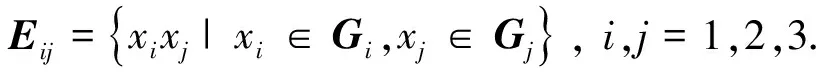
令G1*G2=H1,则E(H1)=E(G1*G2)=E(G1)∪E(G2)∪E12,故有:


所以E(G1*(G2*G3))=E(G1)∪E(G2)∪E(G3)∪E12∪E13∪E23.
令G2*G3=H2,则E(H2)=E(G2*G3)=E(G2)UE(G3)∪E23,所以


故结合律成立,即
(G1*G2)*G3=G1*(G2*G3)
2) 由定义知V(G1*G2)=V(G1)∪V(G2)=V(G2)∪V(G1)=V(G2*G1)
E(G1*G2)=E(G1)∪E(G2)∪E12E(G2*G1)=E(G2)∪E(G1)∪E21
而E12=E21,故E(G1*G2)=E(G2*G1),G1*G2=G2*G1.
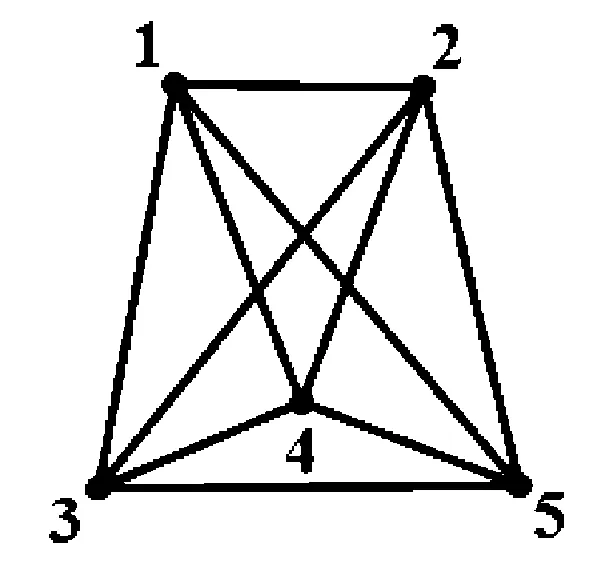
图1 K3*K2=K5

图2 K2×K2=C4
定理2 “*”运算在同构意义下满足以上两条性质:
1) 结合律:(G1×G2)×G3=G1×(G2×G3);
2) 交换律:G1×G2=G2×G1.
所以在图G中,存在一个映射φ,
使φ((x1,y1),zi)=(x1,(y1,z1)),φ((x2,y2),z2)=(x2,(y2,x2)).所以
(G1×G2)×G3≅G1×(G2×G3),所以结合律成立,即(G1×G2)×G3=G1×(G2×G3).
2) 和上面证结合律的方法类似,在图G中,存在一个映射φ,
使φ(x1,y1)=(y1,x1)),φ(x2,y2)=(y2,x2).

⟺ (y1,x1)~(y2,x2)inG2×G1.
所以G1×G2≅G2×G1,所以交换律成立,即G1×G2=G2×G1.
注:两种运算都不满足分配律.
令G1=G2=K1,G3=K2,则
4 “*”运算作用在完全图Kn上的性质
由运算的定义知:
性质1K0*Kn=Kn.(其中K0=Ø表示空图)
性质2Kn1*Kn2=Kn1+n2.

定理3 (K,*)构成代数系统.
证明 由性质2知,对∀Kn1,Kn2∈K,有Kn1*Kn2=Kn1+n2∈K,所以运算封闭构成代数系统.
定理4 (K,*)构成交换半群.
证明 由定理1知,“*”运算满足结合律和交换律,所以构成交换半群.
定理5 (K,*)构成交换幺半群.
证明 由性质1知,K0*Kn=Kn,所以K0是单位元,所以构成交换幺半群.
但是在(K,*)中,任一元素(除K0外)无逆元,所以(K,*)构不成群,下面我们设
注:运算的实际意义:
1)当n1+n2 2)当n1+n2≥n时,Kn1*Kn2=Kn1+n2-Kn∈K[n],即Kn在Kn1+n2中的补图. 定理6 (K[n],*)构成交换群且与(Zn,+)同构. 证明 1)由重新定义知,运算封闭. 2)由定理1知,结合律和交换律成立. 3)由性质1知,对∀Ki∈Kn,有K0*Ki=Ki,所以K0为单位元. 4)对∀Km∈K[n]有逆元,(Km)-1=Kn-m. 所以(Kn,*)构成一个交换群. 存在一个映射φ:K[n]→Zm Ki→φ(Ki) 使得φ(Ki*Kj)=φ(Ki)+φ(Kj)=(i+j)mod(n). 故:(K[n],*)与(Zn,+)同构. 由运算的定义知: 性质3K0×Kn=Ø.(其中K0=Ø表示空图) 性质4K1×Kn=Kn. 但是“×”运算作用在完全图Kn上的运算不封闭,如K2×K2=C4,我们记 定理7 (K,×)构成具有单位元的交换半群. 证明 由性质4知,K1×Kn=Kn,所以K1为单位元; 由定理2知“×”运算满足结合律和交换律;所以(K,×)构成具有单位元的交换半群. 但是在(K,×)中,任一元素(除K1外)无逆元,所以(K,×)构不成群,下面我们设 重新定义在K[m]上的“×”运算: 注:运算的实际意义: 定理8 (K[m],×)构成交换群且与(Zm,+)同构. 证明 因为: 1)由重新定义知,运算封闭; 2)由定理2知,结合律和交换律成立; 所以(K[m],×)构成交换群. 又因为存在一个映射φ:K[m]→Zm 使得(K[m],×)与(Zm,+)同构. [1]Chen Jinyang, Zhu Wenhui, Jiang Binghua. Cyclic edge-connectivity of transformation graph G++-[J].兰州大学学报(自然科学版),2016,52(3):393~395. [2]Chen Jinyang,Super connectivity and Super Edge connectivity of Transformation Graphs[J]. Ars Combinatoria,2012,(105):103~115. [3]Chen Jinyang,Meng Jixiang, Huang Lihong. Super edge connectivity of mixed Cayley graph[J]. Discrete Mathematic,2009, (309): 264~270. [4]Bondy J A,Murty U S R. Graph Theory and Applications[M].New York:Macmillan,Elseiver,1976. [5]Reinhard Diestel.Graph Theory[M].New York:Springer-Verlag,1997. [6]樊 恽,刘宏伟.抽象代数[M].北京:科学出版社,2008. [7]李晓毅,黄风琴.循环群中剩余类加群的讨论[J].沈阳师范大学学报(自然科学版) ,2003,21(3):169~171. Abstract: In the study of graph theory, the operation of graphs is a method of constructing graphs with special properties. This thesis discusses and studies two kinds of operations of graph G in the respect of structure, operation rules and properties, and make it work on complete graphs, so constructing a finite group wnich is isomorphic to the additive groups of surplus. Keywords: complete graph; residue class group of module n; isomorphism Operationalpropertiesoftwokindsofgraphs ZHANG Qian-Nan CHEN Jin-Yang ( College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China) O157.5 A 2096-3149(2017)03- 0053-05 10.3969/j.issn.2096-3149.2017.03.010 2017—04—20 国家自然科学基金项目(71701076),湖北省教育厅青年项目(Q20162504) 张倩男(1993— ),女,天津宝坻人,硕士研究生,主要研究方向为运筹学与控制论.5 “×”运算作用在完全图Kn上的性质