解题能力是学生必备素质——运用还原法提高高中数学解题准确性的对策分析

崔一华

解题能力是学生必备素质
——运用还原法提高高中数学解题准确性的对策分析

崔一华

在高中数学的学习当中，解题能力是受教育者必备的素质之一。高中数学的解题方法有很多，还原法也是其中之一，能够有效地提升解题准确性。此文从运用还原法解决几何类题、运用还原法解决公式定理题以及运用还原法解决技巧性较强的题这三方面对运用还原法提高高中数学解题准确性的对策进行了分析。

解题能力；高中数学；还原法；几何题；公式定理；准确性

随着教育事业的不断发展，对高中受教育者的数学能力的要求也越来越高。数学是一门逻辑性很强的学科，可以锻炼受教育者的思维能力。在高中数学的解题过程当中需要具备发散思维能力，多数受教育者会面临各种各样的困难，不知道从哪里下手找到解题的切入点，这便需要运用多种解题方法，还原法也是众多方法之一，运用还原法来解决问题显得尤为重要。在高中数学解题过程中巧妙地运用还原法可以提升解题的准确性，提升受教育者的解题能力。

一、 运用还原法解决几何类题

在高中数学当中，空间立体几何的三视图是一项重要的内容，同时也是高考当中的高频考点。受教育者在解决这类题型的时候，如果仅仅单凭分析题干，多数人很难解出答案，即便能够分析出答案，也无法确保答案的准确性。

例如：下图给出了一个几何体的三视图，那么下面这个几何体的体积为多少？

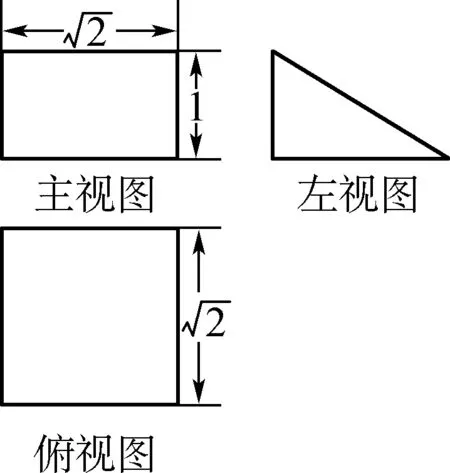
解析：如上图所示，对于这种简单的几何体三视图，单凭看图虽也能够计算出体积，但相对来说还是具有一定的抽象性，也未必有较高的准确性，对那些空间想象力较弱的受教育者来说，仍存在一定的难度。此时，便需要对空间几何体的三视图进行还原。在这个几何体的三视图当中呈现出了两个矩形，通过规律可以得知图当中的空间几何体是柱体。通过观察可发现左视图是一个三角形，因此可以推断这个空间几何体是三棱柱，算出其体积是1。如此一来，运用还原法更容易计算，并且能够提升准确性。

二、 运用还原法解决公式定理题

在高中数学的学习当中，公式定理十分关键，并且被广泛地运用在解题当中，有一部分定理能够正向地应用以及证明。然而，有很多题目当中体现的公式定理并不是显而易见的，面对这样类型的题目，多数受教育者并未将切入点放在题干当中的公式上面，没有多加观察，理不清思路，因此不知道应该采用怎样的解题方法。这个时候便需要对题干进行细心观察，多加分析，对已知条件当中的公式进行还原。

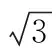
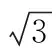
三、 运用还原法解决技巧性较强的题

在高中数学当中有很多技巧相对较难的题目，单凭表面来看，很难找到解题的切入点，令多数受教育者不知从而下手。在解决这种类型题目的时候，也可以运用还原法，有助于找到解题思路的关键点，从而令问题得到快速准确的解决。

例如：设定现在有四个数字，任意取其中三个数字的和，它们分别是40、60、72、80，试着求出这四个数字分别是多少。

解析：这种类型的数学题，在题干当中并未给出太多的已知条件，看上去基本上毫无联系，因此技巧性较强。多数受教育者面对这种类型的题目的时候，往往一头雾水，找不到头绪，更不知从何下手。此时便可运用逆向思维进行还原，找到问题的切入点，题目当中既然已经明确了这四个数字当中任意三个数字的和，那么便可将四个数字的和设为x，通过观察题意，找到已给条件间存在怎样的联系，这道题便很容易找到解。

将四个数字的和设成x，那么便可结合题意将这四个数字分别还原成x-40、x-60、x-72、x-80，并列出(x-40)+(x-60)+(x-72)+(x-80)=x，解得x=84，将x=84代入，因此便可得出这四个数字分别是44、24、12与4，将答案还原于题干当中，44+24+12=80，24+12+4=40，44+24+4=72，44+12+4=60，如此可见，与题意相符。运用还原法解答这样的技巧性问题，不但可以快速理清题意从而找出解题方法，还能够提升解题的准确性，提升受教育者的解题能力。

四、 结束语

综上所述，在对高中数学的解题过程当中，运用还原法是一种有效的解题方法，这种方法能够将原本抽象且很难找到切入点的问题变得清晰直观。在实际的教学当中，广大高中数学教育者应当将还原法有效地运用于数学解题当中，提升解题的准确性，令受教育者的解题能力得到提升，与此同时，还要对相关对策展开积极的探究，获得更加显著的教学成效。

[1]李兆强.高中数学数列的解题常规方法分析[J].数理化学习(高中版)，2015，(7)：2-3.

[2]徐崇明.浅谈高中数学解题思维方法教学策略[J].新课程导学，2016，(26).

崔一华，江苏省宝应中学。