错在哪里

数 学园 地

错在哪里

1新疆生产建设兵团第二中学

张丽娟张国治(邮编:830002)

题目(2017年衡水中学模拟调研卷衡水金卷理科数学(五)第15题)

解析(该试卷提供的标准解答)

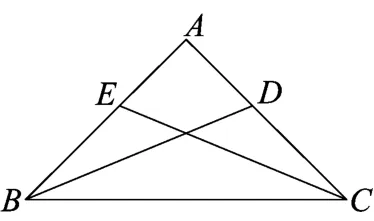
图1

设 ∠A、∠ABC,∠ACB所对的边分别为a、b、c．如图1所示,∠A＝90°,在Rt△BAD 中,BD ＝,在 Rt△CAE 中,,所以．依题意得BD·CE＝4,所以．又由正弦定理,可知,所以bc＝a2sinBsinC．因此,即,从而得到a＝2,故BC边的长为2．

题目错了，错在哪里?

上述题目及解答似乎无懈可击,但却犯了一个致命的错误即符合题意的Rt△ABC是否存在?出题者在编拟试题时有心理上的“潜在假设”,即认为符合题意的三角形是存在的,但实际上本题一开始的前提便是谬误,只得差若毫厘,谬以千里之果．

错误剖析1一个自然的思路是依据题设条件采用“减元”的策略,求出sinB或sinC后由正弦定理获解．

错误剖析2同剖析1,从另外一个角度来探究的取值范围,由式子结构联想到由积化和差公式得,而B、,故即,故,从而,当且仅当B－C＝0,即B＝C＝时,

若能够救偏补弊,此题便不失为一道提升能力训练思维的好题．

试题修正已知Rt△ABC中,A＝90°,且,若B、C的角平分线的长的乘积为4,则BC边的长为______．

试题推广已知Rt△ABC中,∠A＝90°,且,若B、C的角平分线的长的乘积为n,则

解析设∠A、∠ABC、∠ACB所对的边分别 为a、b、c．如 图 1 所 示,∠A ＝90°,在Rt△BAD中,在 Rt△CAE中,,所以．所以．又由正弦定理,可知,即bc＝a2sinBsinC．因此,即4ma2＝n,从而得到,故BC边的长为

由此题我们进行剖析可见,对于题目的编制应遵循条件相容性原则,即题设条件之间不能互相矛盾．此题的错误比较隐蔽,需要深刻地从不同角度剖析．事实上,通过正本清源发现本质的错误在于命题者忽视了Rt△ABC中,∠A＝90°,且这一隐含条件．

解后反思(1)试题编拟过程中题目的条件对于推出结论是充分的,而有些条件不充分的题目之所以存在,是由于编拟试题和解题时有心理上的“潜在假设”,或逻辑上的“以偏概全”．当然,在试题编拟过程中要特别注意隐含条件,题设条件不能与本系统的公理、定理、已知正确的结论等相矛盾,而且题设中的多个条件之间也不能互相矛盾．故我们应注重在解题环节中需要“常回头看看”,养成良好的检查习惯．

(2)数学解题贵在自然．老子说:“出其致远,其知弥少”在重技巧求功利的数学学习过程中,人人都有越发多元的方法和技巧,却也都无意识的离天然越发遥远,对真正的知识基础越发茫然,失去了数学解题中所需的“真、善、美”．殊不知,数学解题及数学教学应该以学生已有的知识基础和经验为出发点和落脚点,跟着学生感觉走,努力寻求自然的解法．当然,自然的解题思路,往往体现在经过科学合理编制、仔细反复推敲的数学试题上．数学方法与数学思想的起源与发展都是自然的．如果有人感到某个概念不自然,是强加于人的,那么只要想一下它的背景,它的形成过程,它的应用,以及它与其它概念的联系,你就会发现它的存在实际上是水到渠成、浑然天成的,不仅合情合理,甚至显得很有人情味．