一个优美不等式的优美简证

(天津水运高级技工学校 黄兆麟 (邮编:300456)

一个优美不等式的优美简证

(天津水运高级技工学校 黄兆麟 (邮编:300456)

安振平先生在文[1]中提出了40个优美的代数不等式,其中第24个为:

若a、b、c是正数,a2＋b2＋c2＝3,求证

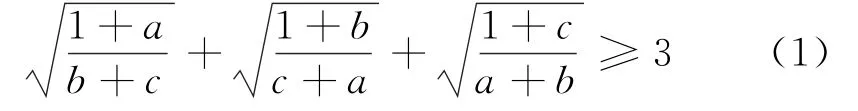
何灯老师在文[2]中称该不等式颇有难度,并利用柯西不等式及构造一个常人不易想到局部不等式,给出了该不等式一种技巧性较高的优美证明．笔者经深入探究此题,发现了一种技巧性较低的优美简证,现介绍如下,与读者分享．

证明 首先将条件等式化为条件不等式

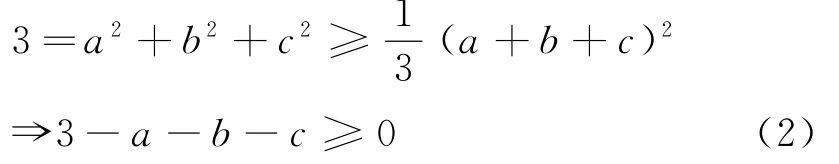
再利用二元均值定理,将不等式(1)左右作差可得

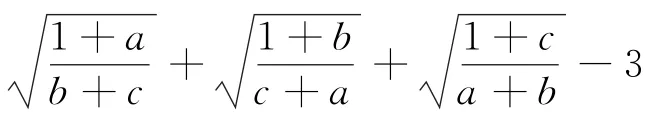
则不等式(1)成立．以上最后一步用到了不等式(2)成立的结论．

点评由以上证明过程可以看出,本文证法之所以如此简捷,原因有二:其一,成功利用了条件等式;其二,利用二元均值定理,将原无理分式不等式加强为有理分式不等式,再证明反而容易多了．可以说,这不是技巧,而是一种方法．

1 安振平．优美的代数不等式[J]．中学数学教学参考(上旬),2015(3):71-72

2 何灯．关于两个优美不等式的证明[J]．中学数学研究(江西)2016(7):46-47

2017-07-10)