2017年高考三角题的探究剖析及教学启示
合肥工业大学附中 余树宝 (邮编:230009)
2017年高考三角题的探究剖析及教学启示
合肥工业大学附中 余树宝 (邮编:230009)
2017年高考数学新课标全国卷Ⅰ理科第17题:
已知△ABC的内角A、B、C的对边分别为a、b、c,且 △ABC的面积为
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求 △ABC的周长.
我们试图就此题的来龙去脉,来透视命题者的理念与意图,探究与剖析此类问题的特点与思路,为今后高效备考三角问题谈谈自己肤浅的认识,供同行参考.
1 追根溯源
为提高备考复习的针对性和有效性,每年高考前使用全国卷的一线老师(也包括学生及学生家长)都积极踊跃地投入到试题研究、猜题押题的队伍中,我们也不例外.不同于分省自主命题,历年全国卷的试题结构、考点分布、难度系数等方面相对比较稳定,于是研究历年考题特点、规律是各地老师乐此不疲.
1.1 延承重点
2017年高考前,重点研究了2014-2016全国新课标理科Ⅰ卷对“三角”内容的考查,试图从中发现端倪,以有效备战2017年高考.
(1)重点考查三角形中的求值问题
2014年第16题:已知a、b、c分别为△ABC三个内角A、B、C的对边,a=2,且(2+b)·(sinA-sinB)=(c-b)sinC,则△ABC面积的最大值为______.
2015年第16题:在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是______.
2016年第17题:△ABC的内角A、B、C的对边分别为a、b、c,已知2cosC(acosB+bcosA)=c.
这三题主要考查正、余弦定理、三角形面积公式及其应用,这是历年高考考查的热点.2014年第16题是利用正弦定理化角为边得b2+c2-a2=bc,再由余弦定理得,于是A=,由基本不等式得bc≤4,再由面积公式得最大值为 3.2015年第16题题考查了数形结合及极限的思想,当A与D重合时,AB最长,当D与C重合时,AB最短,由正弦定理解两个三角形分别得AB的极限长度,于是AB的取值范围为2016年第17题也是由正弦定理化边为角得,于是,再由面积公式及余弦定理得a+b=5,故周长为5+
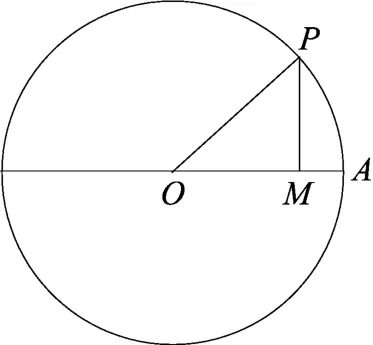
(2)重点考查三角函数的图象与性质问题2014年第6题:如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示成x的函数f(x),则y=f(x)在[0,π]的图象大致为( )
2015年第8题:函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )
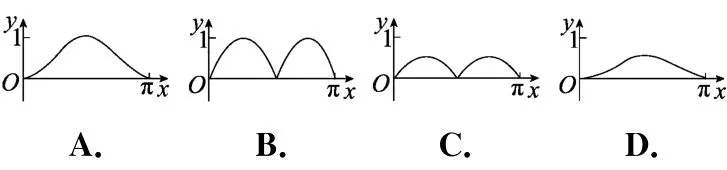
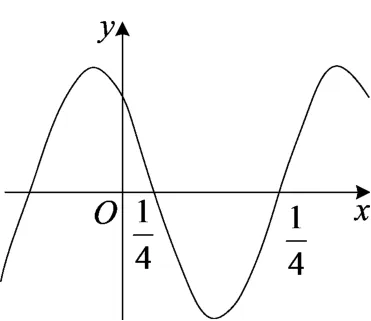
这两题主要考查三角函数的图象与性质.2014年第6题先根据三角函数的定义得点M(cosx,0),后由等积关系得f(x)=|sinxcosx|,故最大值为是其一个零点,故选C.2015年第8题先由图象确定ω=π,φ=,再依余弦函数的单调性,得f(x)的单调递减区间为选项D.
(3)重点考查三角恒等变换问题
2015年第2题:sin20ocos10o-cos160osin10o=( )
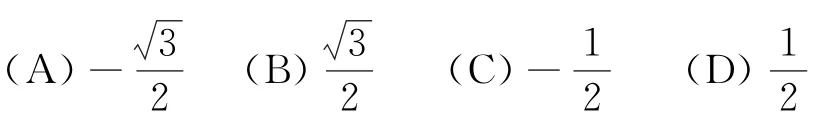
此两题主要考查三角恒等变换,解题主要涉及到诱导公式、两角和与差公式、倍角公式的应用.2014年第8题由已知得考虑正切函数单调性得,故选C.2015年第2题先由诱导公式得原式=sin20°cos10°+,故选D.
纵观历年考题,不难发现高考全国卷对三角函数与解三角形内容的考查,突出了日常教学的重点内容,重点考查三角函数的图象与性质,三角公式在求值、化简中的应用,正、余弦定理、面积公式在解三角形中的应用.同时,我们也关注到2014、2015年对三角问题考查的试题出现在选择、填空题中,2016年仅在解答题中出现三角问题.另外,我们还发现,全国卷理科第17题(即解答题第一题)呈现出两个数列、两年三角的变化规律,所以在2017年考前我们就估计2017年高考第17题仍将会考查三角问题,重点会考查三角形中的求值问题或三角函数的图象与性质问题.2017年高考后,我们再次觉得研究历年高考试题对备战高考非常重要.
1.2 源于教材
严格来说,高考命题是依据部颁《普通高中课程方案》和《普通高中数学课程标准》的必修课程、选修课程的内容来确定考试内容,因此高考试题的来源往往是课程内容的再现、综合和深化.细心观察,多数历年的考题都均在教材中找到源头.
例如,2016年高考第17题源于人教A版第一章《解三角形》1.2《应用举例》课后练习题第3题:“在三角形中,求证:c=acosB+bcosA.”利用此题结果,轻松得到于是
2017年高考第17题也不例外,它源自并深化于人教A版第一章《解三角形》习题1.2B组第1题:“证明三角形的面积公式如果利用此题结果,由易得
由此说明高考试题虽然高于课本,但是源于课本,这也是为什么每年高考试题都给人以“似曾相识”感觉的原因.
作为一线数学老师,我们依据全国卷高考试题稳定性的特点,深入研究历年高考真题,可以预测高考题的“前世”;根据全国卷高考试题高于课本、源于课本的特点,回归教材,深化课本,可以寻索高考题的“前世”.当你知道她是从哪里来,你才有可能知道她会往哪里去.知己知彼,百战不殆,对于备战高考也是如此.
2 试题探究
2017年高考题的诞生,她的“容貌”及“内涵”引起诸多老师的关注,喜欢与不喜欢、欣赏与不欣赏,她还是她,我们都必须接受,零距离接触,你会发现她真的很“美”,值得研究.2017年理科第17题较全面地考查了两角和与差公式、正弦定理、余弦定理、面积公式及其应用,考查运算求解能力、分析问题和解决问题等能力.
2.1 问题(1)剖析
审好题是解好题的前提.审题时,要弄清楚试题给什么及求什么,要抓住已知中的有效条件.此题中“△ABC的内角A、B、C的对边分别为a、b、c”不是有效条件,它是一个习惯性的约定.问题中有效条件是“△ABC的面积为”,由此来求sinBsinC,涉及面积,自然我们应该想到三角形面积公式.
三角形面积公式常用的有两组(当然它们之间可以相互推导):选择也是一种能力,选择哪一组公式最适合问题的解决是关键,此时要结合需要解决的问题来做选择.由于题设中“△ABC的面积为”,故应选择含有边角关系的面积公式,但这三个选一个也有讲究,因中含sinA,故应优先考虑S△=与已知相等,然后利用正弦定理“化边为角”即可得到问题(1)sinBsinC的值.当然,选择另外两个也可求解.
第(1)问解答(略解):
解法1由,得a2=,由正弦定理得sin2A,又sinA≠0,得
解法3由,化边为角得,于是
解法2由化边为角得,于是
2.2 问题(2)剖析
问题(2)是在问题(1)解决的基础上,增加两个条件求此三角形的周长,即求b、c的值.由这样的条件求边长,还是有别于历年常规.如2016年第17题,同样是求 △ABC的周长,但它的条件很常规:,△ABC的面积为因为它至少告诉六个边角元素中的两个.而今年这种“不走寻常路”的做法,应该说也是一种“创新”.怎样用好sinBsinC与cosBcosC的值这两个条件,对考生来说一种能力的考验.从方程的角度来说,两个未知数两个方程应该可以分别求B、C的大小,再加上a的值已知,此三角形可解.但是不是真的能求出B、C的大小,是不是有必要去分别地去求B、C的大小,也是值得商榷的.事实上,要求此三角形的周长,只需要求出b+c的值即可,这是考生应该具备的整体性思想.
第(2)问解答(略解):
解法1由及已知6cosBcosC=1,得
由余弦定理a2=b2+c2-2bccosA,得(b+c)2=9+3bc, ①
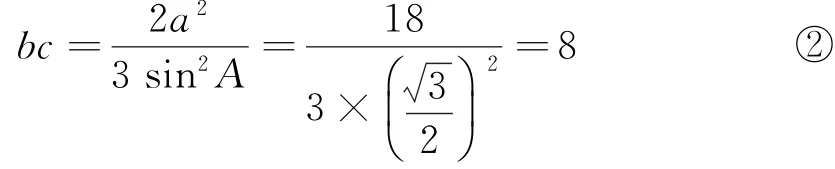
解法2由(1)中及6cosBcosC=1,得
解法3由及6cosBcosC=1,得
3 教学启示
三角函数,作为高考的重要内容之一,相比其它重点内容,虽然难度不大,但从日常教学测试中发现,学生得分率往往并不是很高,究其主要原因,还是师生对三角内容的复习重视程度不够,“轻视”导致“忽视”.除态度上要高度重视外,建议我们的备考复习还要注意以下两点:
3.1 立足教材
教材内容是最基本的数学文化知识,无论高考考题怎么命制,都要用教材中的知识及其中蕴含的数学思想方法去解决.如果考生连教材中最基本的概念、公式、定理等就没有掌握,那么想顺利解决那些以能力立意的试题,几乎是不可能的.因为基础知识是数学能力提升的基础与前提,故回归教材是正道.
特别是教材中的数学概念、性质、法则、公式、公理、定理以及由其反映的数学思想方法,还包括按照一定程序与步骤进行运算求解、数据处理、图表绘制等基本技能,要加以分类、梳理、归纳和总结.另外,对教材中一些典型的例、习题要加以剖析和深化,籍此来提高学生的逻辑思维能力和分析问题解决问题能力.
教学中要做到重点内容重点复习,突出“二三四”,即:两大问题(三角形中的求值问题、三角函数的图象与性质问题)、三个定理(内角和定理、正弦定理、余弦定理)、四大公式(同角三角函数基本式、诱导公式、两角和与差公式、二倍角公式,及其变形后的公式,如辅助角公式、降次公式),因为多年来高考始终坚持重点内容重点考查,抓住了重点,才能做到有的放矢,复习才能有针对性,也才能有备考的高效率高质量.
3.2 强化思维
高考承载着国家选拔人才的任务,为了把具有较强思维能力与创新能力的考生选拔出来,命题专家就会打破常规,设计出一些新颖的试题,以考查考生的应变能力.
作为教师,一定要改变过去那种把学生看作解题机器,埋头讲题刷题,强调学生机械记忆,以题海战术代替数学思维的培养,以经验积累代替理性思考,以操练代替创新.教学中注重分析解题思路是怎样形成的,解决问题的方法怎样想到的,否则,我们培养的学生就养成了善于模仿,思维定势,创新能力缺失,灵活应变能力薄弱.如平时备考资料中经常出现形如asin2x+bcos2x的问题,遇此问题,学生都知道用降幂公式将它化为asinx+bcosx的形式,接着用辅助角公式化成 a2+b2sin(x+φ)形式,然后就可以求解此函数的图象与性质问题.化简此函数解析式的目的是什么?方向是什么?如何做?为什么要这样做?这样做是为什么?这些问题一定要与学生讲明白,只有这样,学生在考试中遇到近似或远似的问题,他的思路就会清晰,不至于问题条件的变化而导致问题的解决无从下手.再如今年高考第17题(2)问,用sinBsinC、cosBcosC及a的值来求三角形周长,条件平凡而不俗,体现了命题者的独具匠心,值得我们深思!
总之,三角问题每年都会考,但常考常新,不落俗套,只有我们帮助学生夯实基础,强化能力,才能应对挑战,取得高考的成功.
2017-07-18)
安徽省教育科学研究课题“名师工作室平台下的教师专业发展策略的研究”(项目编号:JKZ1703)
基金项目:本文系广东省教育科研“十三五”规划项目课题《渗透数学的真善美,提升初中数学教育的价值》研究成果(课题批准号2016YQJK168)

