圆都去哪儿了
——巧找隐圆解决线段范围问题
江苏省常州市田家炳高级中学 徐 颖 (邮编:213000)
解 题方 法
圆都去哪儿了
——巧找隐圆解决线段范围问题
江苏省常州市田家炳高级中学 徐 颖 (邮编:213000)
纵观近几年的高考,对轨迹问题的考查基本分两类:一类是“显性”的[1],即常见的求动点的轨迹方程问题,其实质就是用“坐标化”将条件转化为变量间的数量关系,如2010年江苏卷第18题.这类问题除了考查学生对常见曲线的定义、性质等基础知识的掌握外,还充分考查了各种数学思想方法及一定的推理能力与运算能力;另一类是“隐性”的[1],即无明确的求轨迹任务,但轨迹却实实在在地存在,或者说它更强调的是一种“轨迹意识”,而这方面思想与意识的缺失,往往直接导致问题难于解决或无法解决.如2008年江苏卷第13题,2009年江苏卷第18题,2010年江苏卷第9题,2013年江苏卷第17题,2016年江苏卷第18题等.学生不容易把握解题方向,望而却步,导致丢分严重.
近年来,几何最值问题在高考中频繁出现,形式多样,其中线段的最值问题比较受青睐.这类线段大致具有如下特点:两个端点一定一动;两个端点都在动.动态背景下,求线段范围问题有难度,追踪相关动点的生成过程,研究其运动轨迹,就能顺利解决问题.本文我们针对具体题目,探究隐圆在解决线段范围问题中的运用.
1 圆的定义
例1已知F1、F2是双曲线x2-y2=4的两个焦点,Q为双曲线上任意一点,过点F1作∠F1QF2的平分线的垂线,垂足为P,若M(-3,-4),求线段PM的取值范围.
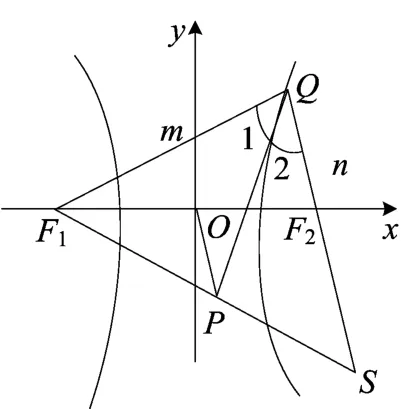
图1
解如图1,设QF1=m,QF2=n,延长F1P、QF2交于S,由于 ∠1=∠2,PQ⊥F1S,所以QF1=QS,根据双曲线的定义可得F2S=QSQF2=QF1-QF2=m-n=4.
又O、P分别为F1F2、F1S的中点,所以OP是△F1F2S的中位线,OP=2.
故点P的轨迹方程是x2+y2=4.
又M(-3,-4)在圆外,故PMmax=OM+r=7,PMmin=OM-r=3.
故PM∈[3,7].
例2在平面直角坐标系xOy中,设A、B、P是椭圆上的三个点,且0,动点Q在线段AB上,且求的取值范围.
解以O为极点,Ox轴正半轴为极轴建立极坐标系.
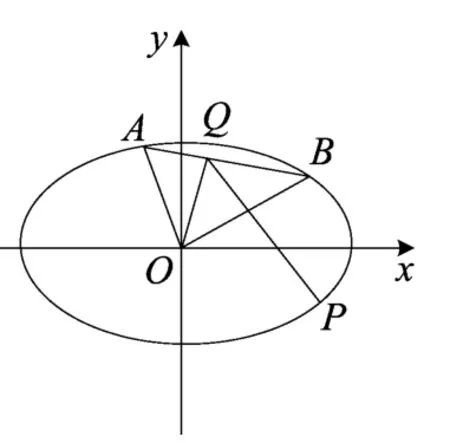
图2
即A(-nsinα,ncosα).

评析本题P、Q均为动点,而已知点P在定曲线椭圆上,因此首要任务是找到点Q的轨迹,而动点Q(x,y)的坐标之间的关系不易找到,故考虑将x、y用一个或几个参数来表示,消去参数得轨迹方程.选用什么变量为参数尤为重要,要看动点随什么量的变化而变化,常见的参数有:斜率、截距、定比、角、点的坐标等.本题可以设OA或者AB的斜率,但是计算相对繁琐.本题中OA、OB都是从原点出发的线段,虽然长度不等,但是有方向上的垂直关系,而解析几何的核心是“坐标法”,于是不妨设成极坐标系来解决.例1、例2都是根据题中的几何条件得出一个长度确定的线段,从而联想到圆的定义,这是一个从“形”到“形”的过程.
2 圆周角的性质
例3实数a、b、c满足3a+4b+c=0,过点P(-3,2)作直线l:ax+by+c=0的垂线,垂足为M,点N(8,-3),求线段MN长度的取值范围.
解由题意3a+4b+c=0得c=-3a-4b,代入直线方程得ax+by-3a-4b=0,即a(x-3)+b(y-4)=0,直线恒过点Q(3,4).又PM⊥l,即PM⊥MQ,故点M的轨迹是以PQ为直径的圆,方程是x2+(y-3)2=40.圆心R(0,3),点N在圆R外.
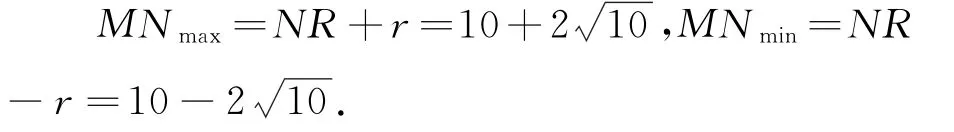
评析首先根据a、b、c的关系得到直线过定点,根据两直线垂直关系得到交点的轨迹是圆,问题就解决了.圆周角有丰富的几何性质,如同弧所对的圆周角相等;直径所对的圆周角为直角;圆内接四边形对角互补等.联想到这些性质,便于挖掘出隐圆,快速解题.
3 动点与两定点的距离有数量关系

图3
例4(南通,泰州2017届调研卷1)在平面直角坐标系中,已知B、C为圆x2+y2=4上两点,且A(1,1),AB⊥AC,求线段BC长度的取值范围.
解取BC的中点M,连 结 OM、AM、OB.由 于AB⊥AC,故AM=BM.
在Rt△BMO中,OB2=OM2+BM2=OM2+AM2=4.
设M(x,y),故x2+y2+ (x-1)2+(y-1)2=4即
评析例4中B、C均为动点,直接下手求长度范围很困难.又发现BC为已知圆的弦,故考虑从弦长公式下手,找到弦BC的中点M,根据直角三角形的性质,将BC转化为2AM,而点M到两定点O、A的距离的平方和为常数,最终确定轨迹是圆Q,于是本题转化成定点A到圆Q上任一点距离的最值.另外,我们还需要关注:①到两个定点的距离的平方差为定值的点的轨迹是直线;②到两个定点距离之比为常数(不等于0和1)的点的轨迹是圆.
4 主动点与从动点
例5(2017届高三扬州期末)
已知△ABC是边长为3的等边三角形,点P是以点A为圆心的单位圆上一动点,点Q满足,求的最小值.
解以A为原点,AB为x轴建立平面直角坐标系,则设Q(x,y)、P(a,b),由得
两式平方并相加得
评析相关点法也称“代入法”,如果轨迹动点Q(x,y)依赖于另一动点P(a,b),而P又按某个规律运动,则可先用x、y表示a、b,再把a、b代入它满足的条件便得到x、y的关系,即得到了动点Q(x,y)的轨迹方程.本题求线段BQ的最小值,其中B是定点,Q随着P的运动而运动,通过建系,运用相关点法即可求出Q的轨迹,接下来问题转化为定点与圆上动点距离的最小值.
5 无理方程
例6已知实数x、y满足x- x+1=y+3-y,求x+y的最大值.
解设 x+1=a,y+3=b,则
原式化简为a2-1-a=b-b2+3,即问题转化成求x+y=a2-1+b2-3=a2+b2-4的范围.a2+b2-4表示上述圆上任一点(a,b)与原点距离的平方减去4,(x+y)max=(OQ+r)2-4=4.
评析例6是典型的代数问题,一个带根式的二元一次方程无法解出x、y,但是通过根式换元,对条件进行变形和整理,转化为几何问题,实在是巧妙.
以上几个例子我们充分挖掘了问题中的隐圆.在平面解析几何中,很多题目中对动点的轨迹往往只字不提,甚至连“动点”这样的关键词都不出现,而只是提供一些“安静”的点、位置、距离或者数量关系,而在这“安静”的表象背后却隐藏着点的运动变化,我们若能化“隐性”为“显性”,就找到了此类问题的核心所在!其实不仅圆有“隐性”轨迹,其他圆锥曲线也有类似问题.在平时的教学中,如何突出重视“轨迹思想”“轨迹意识”的培养与训练,以提升学生解决问题的能力,这才是最根本的.
1 童其林.隐性轨迹问题[J].数学教学,2010(8):24-26
2017-06-26)

