基于SAS算法的飞行器低空突防三维航路规划研究∗

孙 涛 刘家祺 张龙杰 樊鹏飞 周 涛

基于SAS算法的飞行器低空突防三维航路规划研究∗

孙 涛1刘家祺1张龙杰1樊鹏飞1周 涛2

（1.海军航空工程学院兵器科学与技术系 烟台 264001）（2.海军航空工程学院学员二旅 烟台 264001）

SAS算法的各个主要搜索参数对飞行器航路规划的结果影响关系复杂，论文在对低空突防三维航路规划进行仿真实现的基础上，对最小步长搜索步长、扩展节点数、代价函数权重、最大飞行高度、最大转弯角等主要搜索参数进行了多组数据仿真对比，分析了各个参数对低空突防航路规划结果的影响关系，对于基于SAS算法进行飞行器航路规划的改进和优化具有参考意义。

SAS算法；飞行器；低空突防；航路规划

AbstractThe influence of SAS parameters on aircraft low altitude penetration route planning is complicated.Based on the simulation of aircraft low altitude penetration，the influence of the main searching parameters，such as the min searching step，the number of extended nodes，the weight of cost function，the max flight altitude，and the max turn angle are compared by several groups of simulation with different parameters.The relation between SAS parameters and route planning result is analyzed，which has some reference significance in aircraft low altitude penetration route planning improvement and optimization.

Key WordsSASalgorithm，aircraft，low altitude penetration，route planning

Class NumberTP39

1 引言

飞行器低空突防航路规划属于路径寻优问题，目前较为多见的航路规划算法研究主要有简单几何规划方法、遗传算法［1］、蚁群算法［2］、Voronoi图［3］、A*［4］及其改进的 SAS（稀疏 A*）算法［5～7］、D*优化算法［8］，以及鱼群算法［9］、粒子群优化［10］等多种方法。其中，SAS算法可证明能够找到最优解，并且具有可解析的求解过程，因此研究和应用比较广泛。

SAS算法的各个搜索参数对航路规划结果的影响关系比较复杂，给实际的航路规划实现带来困难，因此，有必要对给各参数的影响规律进行分析。本文通过仿真实验分析算法搜索所得航路的总代价、搜索时间以及储存数据空间与所采用的搜索参数之间的关系。

2 算法描述

A*算法是一种启发式搜索算法。通过设置启发函数，然后通过迭代的方法选择下一个满足最小代价的航路点，进行航路扩展，从而得到一条最优航路。该算法通过设置启发函数来寻找下一个节点进行扩展。启发函数是从起始航路点至当前航路点的实际代价函数值和从当前航路点到目标点的估计代价函数值加权得到的。也就是说飞行器低空突防航路规划的启发函数由两部分组成，一部分是飞行器已经飞行过的航路产生的代价也称历史代价，另一部分是飞行器将要飞行产生的代价也称估计代价。启发函数也称代价函数。A*算法的总代价函数的形式如下

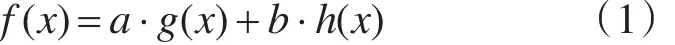
式中：f(x)是整个航路的代价；a、b分别是真实代价函数值和估计代价值的加权系数；g(x)、h(x)分别是从起始航路点到当前航路点的真是代价函数，以及从当前航路点到目标点的估计代价函数，由于三维低空突防航路规划中希望飞行高度尽可能低，因此在代价函数中除了包含三维航程代价外，通常还包含航路各节点离地高度的最大值、平均值和方差的加权值。

在使用A*算法进行航路规划时，总是选择总代价值的航路节点进行扩展，从而保证从起点到目标点的真实代价达到最小，得到一条最优的航路。

SAS算法在进行搜索时，为了精简搜索空间，缩短规划时间，就需要把每一个航路点可能有的扩展空间划分若干个子空间，只在每个子空间内找一个点进行可能的航路扩展。每个子空间的航路点不是随意确定的，被选择的子空间航路点是当前子空间中代价最小的点，然后从当前节点对选择的子节点进行扩展。

3 三维扩展设计

三维航路规划中，SAS算法在水平方向和垂直方向进行航路节点扩展，其扩展过程如图1所示。

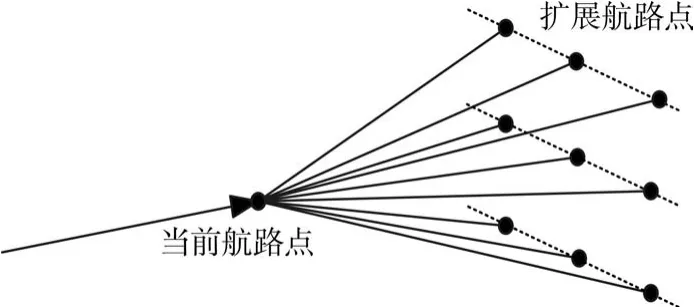
图1 航路节点三维扩展示意图

扩展航路点与当前航路点之间的距离是最小搜索步长；在进行每一步节点扩展时，垂直方向上的角度改变由飞行器的最大爬升/下滑角确定；水平方向上的角度改变由飞行器的最大转弯角确定。这样，形成了一个以当前节点为顶点的锥形扩展区域，再将该区域划分成若干子区域，每个子区域选取所有可能扩展节点中总代价最小的作为SAS算法的一个扩展节点。

每一次进行扩展时都选择当前所有待扩展节点中总代价最小的节点进行扩展，同时将该节点按照排序规则插入到已扩展节点的存储结构中。直至算法完成。对于扩展得到的子节点，先进行约束条件判断，仅保留其中满足所有约束条件并且与现有待扩展节点不重复的节点。节点扩展及存储的过程如图2所示。

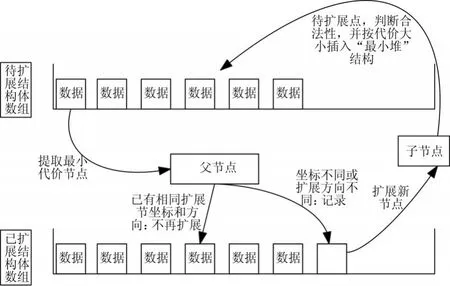
图2 节点扩展及存储

经过反复的节点选取和扩展后，当最终到达目标时，就可以沿着航路搜索树逆向回溯至初始点，从而得到一条最优航路。

4 SAS算法仿真实验系统

仿真系统中采用了栅格形式的地形数据，可以从外部标准文件中导入，也可模拟生成。如图3所示。

图3 仿真系统提供的地形数据

在仿真地形中，可按地形坐标设置初始点或目标点。采用前文所述SAS算法进行低空突防三维航路规划。通过记录算法搜索过程的时间和空间消耗情况，研究SAS算法主要参数对搜索结果和搜索过程的影响。单飞行器低空突防的仿真效果如下图所示，包括航路规划结果、主干扩展节点和航路高程剖面图等。如图4～图6所示。

5 主要参数对算法搜索结果的影响

在模拟仿真地形中，设置初始点三维坐标为（30，40，20），目标点三维坐标为（160，140，10）。通过调整改变各个搜索参数，考察SAS算法搜索效果的影响因素。

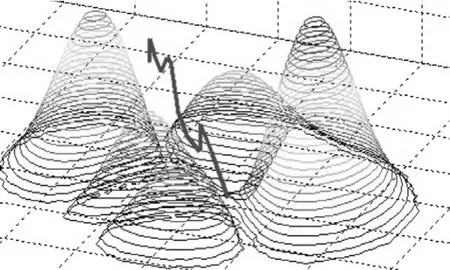
图4 航路规划结果的三维视图

图5 航路二维视图及主干扩展节点

图6 航路高程剖面图

默认设置为：每个父节点的子节点扩展在高度上分为上中下3层，每层扩展数目为3，实验中仅改变每层的扩展数目，而不改变扩展层数，节点扩展方向取为当前节点在每一高度层的正前方和±30°三个方向；SAS算法代价函数的权重稀疏取为a=b=1，飞行器最大飞行高度设为40，最低飞行高度设为5。时间单位为秒，数据储存空间单位为1个节点结构体所占用的字节数。

5.1 最小步长对SAS搜索的影响

最小步长L（以仿真地形网格为单位）是SAS算法中父节点到子节点的扩展距离。通过改变最小搜索步长L，对比实验数据如表1所示。

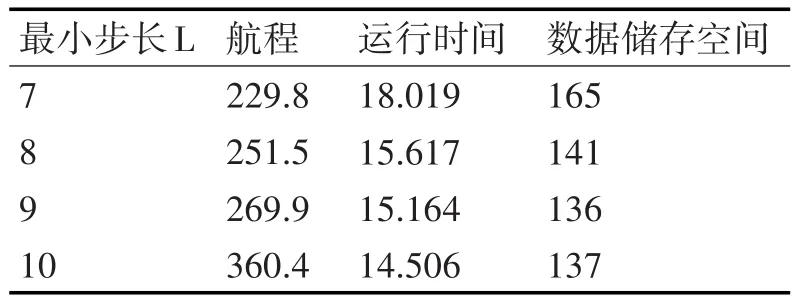
表1 最小步长对SAS算法的影响

分析实验结果可知，在其他参数值不变的情况下，步长增大时，算法运行时间和所占用的储存空间有所减少。这实质上是在牺牲航路搜索精度的情况下，加快了算法收敛速度。工程应用时，可根据实际情况反复实验对比选取。

5.2 扩展节点数对航路规划的影响

稀疏A*算法中，扩展节点数是对当前父节点一次扩展所得到的子节点数目。最小步长L取为9，通过改变节点扩展数目，对比实验数据如表2所示。

表2 扩展节点数对SAS算法的影响

分析实验结果可知，扩展节点数增大，规划结果更优化。因为稀疏A*算法在进行航路扩展时，是将前方的扩展空间分成等分的多个子区间，从每个子区间中找该区间的最优点作为可能的扩展点。每增加一个扩展节点，就会多一种优化选择，遗漏优化航路点的可能性减小。

5.3 代价函数权重对航路规划的影响

稀疏A*算法的代价函数由两部分组成。一部分是待扩展节点的历史航路代价，另一部分是待扩展节点到达目标点的估计剩余代价。权重值体现了历史代价和估计剩余代价在代价函数中的比重。通过改变权重组合，对比实验数据如表3所示。

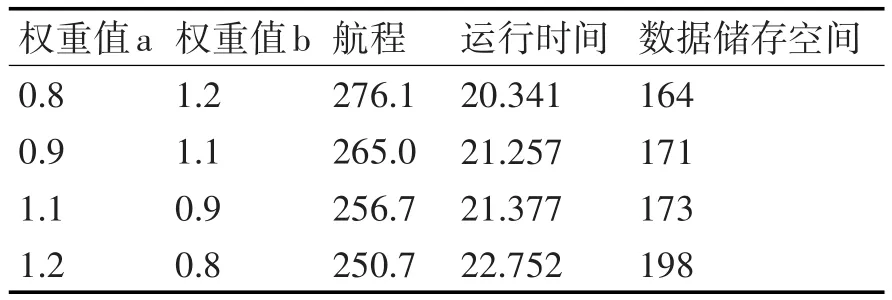
表3 代价权重对SAS算法的影响

分析实验结果可知，在本次实验所用的地形条件下，增加历史代价的权重，能够得到更加优化的结果，但会消耗更多的计算时间和空间。实际上，权重值的改变并不是直接影响规划结果，往往需要根据规划问题所采用的具体地形分布情况，通过反复调整对比来确定适合某一地形环境的规划问题的权重值。也就是说在不同的情况下有着不同的一组权重值使得当前规划问题的结果更优化。

5.4 最大飞行高度航路规划结果的影响

最大飞行高度是由于飞行器升限，以及为了某种战术效果或提高飞行生存概率而设定的约束条件。通过最大飞行高度，对比实验数据如表4所示。

分析实验结果可知，最大飞行高度增高，算法运行的时间趋短，占用存储空间趋少。这是因为，允许的飞行高度越高，飞行器必须规避的地形越少，从而需要更少的航路点和算法搜索时间，相当于减少了规划问题的规模和难度。

表4 最大飞行高度对SAS算法的影响

5.5 最大转弯角对航路规划结果的影响

最大转弯角限定了子节点偏离其父节点飞行方向的最大绝对值。通过改变最大转弯角，对比实验数据如表5所示。

表5 最大转弯角对SAS算法的影响

分析实验结果未见最大转弯角对规划结果的直接影响。原因是改变最大转弯角的选取与规划问题的地形分布，以及初始点、目标点相对态势有关，而对算法总的搜索节点数、问题的规模和难度均没有实质影响。

6 结语

本文针对SAS算法进行了飞行器低空突防三维航路规划的仿真实验，并对该算法的各个搜索参数对航路规划结果的影响进行了分析，得出了各因素的影响规律。

实际的航路规划问题可能是多种因素同时变化和相互影响的结果，后续将深入研究各种典型地形分布特征或者典型任务要求下，多个搜索参数协同变化对飞行器三维航路规划的影响规律及其优化方法。

［1］席庆彪，李康，刘慧霞.振动遗传算法在无人机三维航路规划的算法研究［J］.火力与指挥控制，2014，39（10）：30-35.

XIQingbiao，LIKang，LIUHuixia.Research on UAV Path Planning Based on Vibrational Genetic Algorithm in 3D［J］.Fire Control&Command Control，2014，39（10）：30-35.

［2］程琪，荆涛，于志游.利用三次样条改进蚁群算法的无人机航路规划［J］.计算机测量与控制，2016，24（8）：272-274.

CHENG Qi，JING Tao，YU Zhiyou.UAV Path Planning Based on Ant Colony Optimization Improved by Cubic Spline［J］.Computer Measurement&Control，2016，24（8）：272-274.

［3］聂俊岚，张庆杰，王艳芬.基于加权Voronoi图的无人飞行器航迹规划［J］.飞行力学，2015，33（4）：339-343.

NIE Junlan，ZHANG Qingjie，WANG Yanfen.UAV path planning based on weighted-Voronoi diagram［J］.Flight Dynamics，2015，33（4）：339-343.

［4］李太平，陈艳，袁大天.航路规划的试飞评估技术初步研究［J］.电子测试，2016（12）：40-41.

LI Taiping，CHEN Yan，YUAN Datian.Preliminary study on flight test evaluation technology of route planning［J］.Electronic Test，2016（12）：40-41.

［5］焦卫东，程颖，柯然.基于SAS算法的起飞一发失效应急 路 径 规 划 方 法［J］.航 空 学 报 ，2016，37（10）：3140-3148.

JIAO WD，CHENG Y，KE R.A path planning method for EOSID based on SAS algorithm［J］.Acta Aeronautica et Astronautica Sinica，2016，37（10）：3140-3148.

［6］谢晓方，孙涛，欧阳中辉.反舰导弹航路规划技术［M］.北京：国防工业出版社，2010.

XIE Xiaofang，SUN Tao，OUYANG Zhonghui.Anti-ship missile route planning technology［M］.Beijing：National Defence Industry Press，2010.

［7］谭雁英，胡淼，祝小平，等.基于人机合作策略下SAS算法的多无人机路径再规划［J］.西北工业大学学报，2014（5）：688-692.

TAN Yanying，HU Miao，ZHU Xiaoping，et al.Path Re⁃planning Approach for Multiple UAVs Based on SAS（Sparse A*Search）Algorithm under Human Automation Collaboration［J］.Journal of Northwestern Polytechnical University，2014（5）：688-692.

［8］吴剑，张东豪.基于改进D*算法的无人机航路规划及光顺［J］.航空科学技术，2013（6）：69-71.

WU Jian，ZHANG Donghao.UAV Route Planning and Smoothing Based on Improved D*Algorithm［J］.Aeronau⁃tical Science&Technology，2013（6）：69-71.

［9］沈华，陈金良，周志靖，等.无人机作战对目标点的航迹规划方法研究［J］.计算机仿真，2016，33（9）：73-76.

SHEN Hua，CHEN Jinliang，ZHOU Zhijing，et al.The Method Research for Target Point Path Planning for Target Point of UAV［J］.Computer Simulation，2016，33（9）：73-76.

［10］孙健，吴森堂.基于改进粒子群优化算法的巡航导弹航路规划［J］.北京航空航天大学学报，2011，37（10）：1228-1232.

SUN Jian，WU Sentang.Route planning of cruise missile based on improved particle swarm algorithm［J］.Journal of Beijing University of Aeronautics and Astronautics.2011，37（10）：1228-1232.

3D Route Planning for Aircraft Low A ltitude Penetration Based on SASA lgorithm

SUN Tao1LIU Jiaqi2ZHANG Longjie1FAN Pengfei1ZHOU Tao2
（1.Department of Ordnance Science and Technology，Naval Aeronautical and Astronautical University，Yantai 264001）（2.No.2 Cadets’Brigade，Naval Aeronautical and Astronautical University，Yantai 264001）

TP39

10.3969/j.issn.1672-9722.2017.09.014

2017年4月5日，

2017年5月15日

中国博士后科学基金项目（编号：2013T60923）资助。

孙涛，男，博士，讲师，研究方向：导弹航路规划。