增加副瓣抑制机制的阵列天线波束赋形遗传算法研究

郑占旗 阎跃鹏 张立军 王宇灏 张金玲 慕福奇



增加副瓣抑制机制的阵列天线波束赋形遗传算法研究

郑占旗*①阎跃鹏①张立军①王宇灏①张金玲②慕福奇①

①(中国科学院微电子研究所 北京 100029)②(北京邮电大学电子工程学院 北京 100876)

基于遗传算法的激励优化算法是求解阵列天线波束赋形问题时常用的激励求解算法。传统遗传算法在优化阵列天线激励时，对阵元天线方向图矢量叠加获得阵列天线合成方向图后，与目标方向图做相似度判断，经过多次运算获得满足设计要求的激励值。然而算法中通常不关注赋形结果的副瓣抑制，导致阵列天线波束赋形结果副瓣抑制效果不理想。该文提出一种基于一组低副瓣波束线性叠加的波束合成机制，将合成方向图与目标方向图做相似对比，结合遗传算法的优化求解方法，最终获得与目标方向图匹配的合成方向图，且合成方向图具有高副瓣抑制的特性。以一款16阵元波段微带偶极子线性阵列天线为例，该文提出的具有副瓣抑制机制的遗传算法求得的赋形波束获得了-27.5的副瓣抑制效果，远远好于传统遗传算法求得的赋形波束-19的副瓣抑制。

阵列天线；遗传算法；副瓣抑制

1 引言

余割平方波束在对空监视雷达、塔康雷达和通信基站天线中有着广泛的应用，能在辐射源距离不同的空域提供电场强度均匀的电磁辐射。阵列天线波束的控制参数主要有激励幅度、相位以及天线拓扑结构，当阵列天线拓扑结构的设计完成后，求解满足设计波束要求的阵列天线激励，成了阵列天线波束赋形的首要问题。通常激励的求解通过算法在激励解空间进行选优获得，例如遗传算法，粒子群优化算法，入侵优化杂草算法等。

为了提高副瓣抑制水平，将传统基于阵元天线方向图合成的波束赋形遗传算法转换为基于一组低副瓣波束线性加权叠加的波束合成机制，结合遗传算法波束权值求解，获得了较好副瓣抑制效果的余割平方赋形波束。以一款16阵元波段微带偶极子线性阵列天线波束赋形为例，求得了-27.5的副瓣抑制效果，远远好于传统遗传算法的-12的副瓣抑制效果，且优于文献[10,15,16]中提到的副瓣抑制效果。

2 天线模型

本文以一个X波段微带偶极子阵列天线(如图1所示)为例来说明低副瓣余割平方波束赋形设计方法，图中实线部分为天线正面，虚线部分为天线背面，天线具体参数如下：,。介质板为罗杰斯4350，厚度。由此阵元天线组成16阵元的线性阵列天线，阵元间距为。

3 低副瓣波束合成原理及波束扫描理论

3.1 阵列天线波束合成基本原理

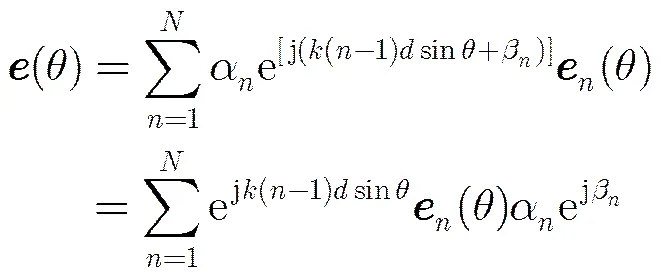
(2)

(3)

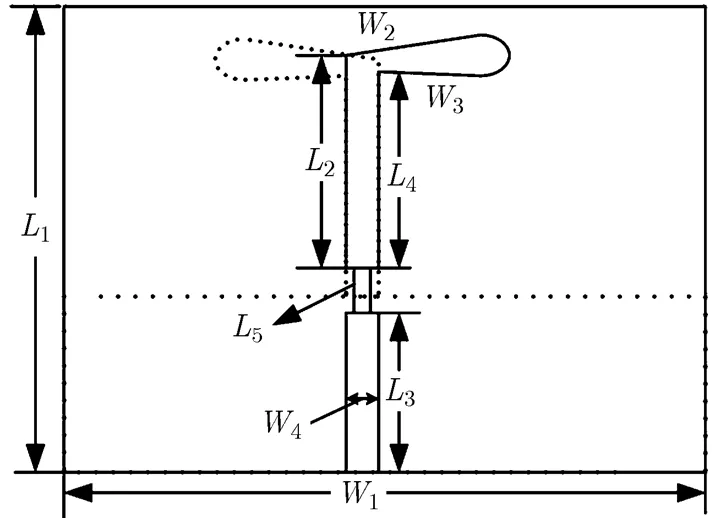
图1 阵元天线结构模型

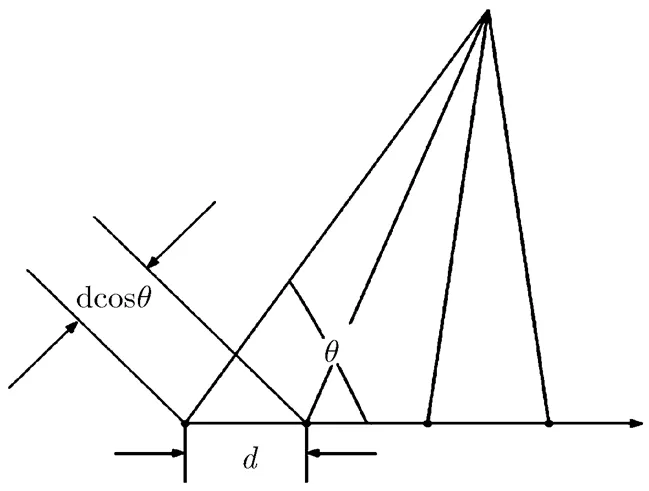
图2 线性阵列天线波束合成原理示意图

3.2 基于幅度为泰勒分布的低副瓣波束分析

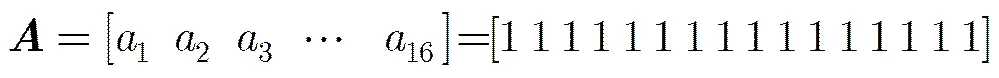
(5)

在副瓣抑制设计中，泰勒分布的激励幅度分布，与等幅分布的激励幅度相比，能较好的抑制副瓣，以下论证基于这种低副瓣波束的方向图赋形遗传算法，推导其理论过程，验证其副瓣抑制能力。

3.3 波束指向角度及波束扫描

对于第2节中线性阵列天线，依据阵列天线扫描理论可知，阵列天线波束指向角可表示为

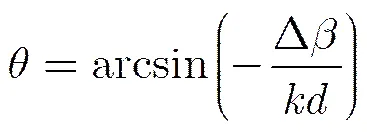
(7)

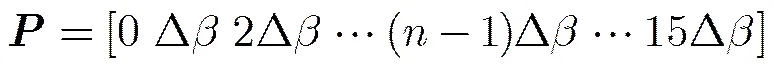
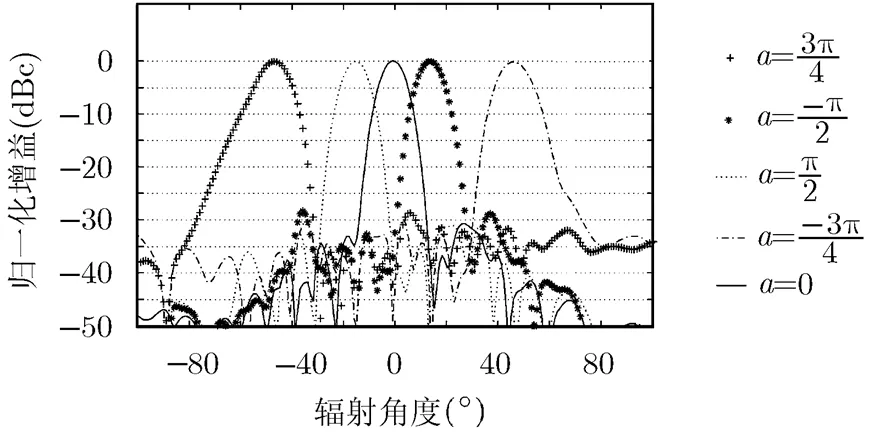
图4 阵列天线基波束指向角扫描

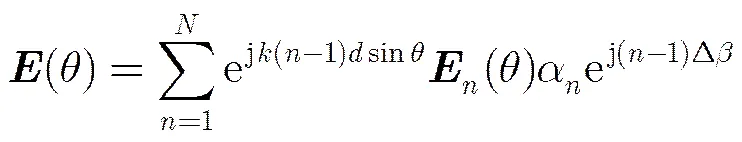
仿真结果表明，这种任意指向的波束均为低副瓣波束，副瓣抑制低于，为方便起见，将这种幅度基于泰勒分布，阵元激励相位间差值为常数的低副瓣波束称为基波束。

4 基于低副瓣基波束的任意波束赋形理论

对如图4所示基波束进行线性加权叠加，产生新的波束。由于每一个基波束，代表了某一窄角度范围内的电场分布，且不同波束间相互独立，因此控制一个波束的权值，则控制了新的合成波束在这个角度范围内的电场分量，实现了任意波束的局部增益独立控制，且这种控制是基于低副瓣的基波束。例如，在角度范围内进行波束赋形，将图4中这类主瓣波束落在范围内的基波束进行线性加权叠加，由于是线性叠加，合成波束主瓣不会落在范围外，而范围外是上述基波束的副瓣叠加而成，由于上述基波束的副瓣均很低，猜测最后合成的波束也是一种低副瓣的可控波束。

下面通过对比赋形区间外增益最大值和赋形区间内增益最大值来证明这种线性加权叠加具有低副瓣的优势：(1)赋形区间外：由于上述加权叠加的权值区间为[0,1]，因此直接对“基波束”进行求和(每个波束权值取为1)，则可得带外增益最大值，以图4中基波束为例，求和后赋形区间外最大增益为(归一化值)；(2)在赋形区间内：至少出现一次权值为1的基波束叠加，因此合成波束在此基波束最大增益位置的加权叠加增益(归一化值)，故在赋形区间内最大增益的取值，对比赋形区间外最大增益，因此可以证明这种波束合成在图4基波束条件下具有至少的副瓣抑制能力。

如果通过权值的选择，将基于一组基波束合成的阵列天线波束方向图控制为目标方向图，进一步寻找此方向图对应的激励矩阵，则获得低副瓣的天线赋形设计。具体分析如下：

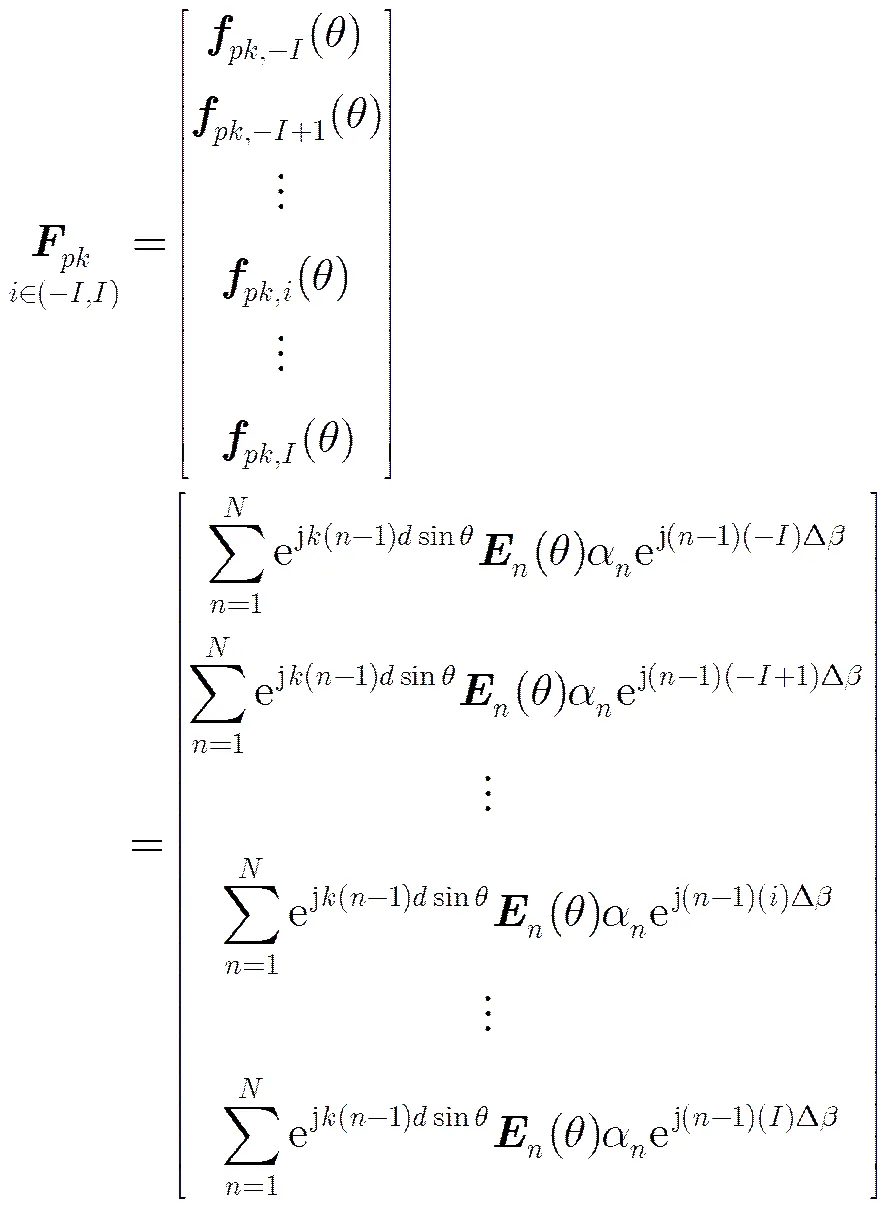
(11)

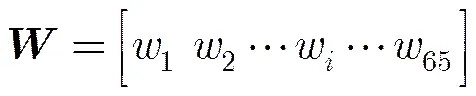
(13)

5 基于低副瓣基波束的任意波束赋形激励求解方法

(15)

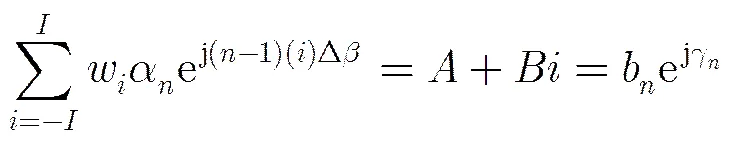
(17)

6 余割平方波束赋形遗传算法研究

以下分别说明传统遗传算法与基于阵列天线低副瓣基波束合成的遗传算法余割平方波束赋形流程。

6.1 传统遗传算法求解余割平方赋形波束设计流程

如图5所示为传统遗传算法阵列天线波束赋形流程，在设计过程中未考虑副瓣抑制问题，因此合成的目标方向图副瓣一般都不理想。

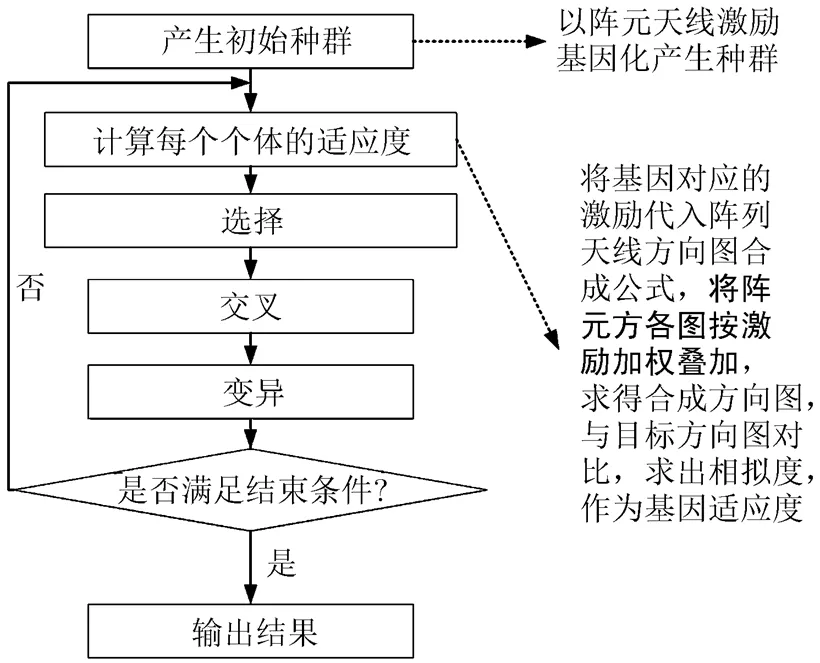
图5 传统遗传算法流程

首先建立初始化基因种群矩阵如式(18)所示，将基因矩阵转换成激励矩阵，代入阵列天线方向图合成公式，得到合成方向图，将合成方向图与目标方向图对比，比较其相似度。

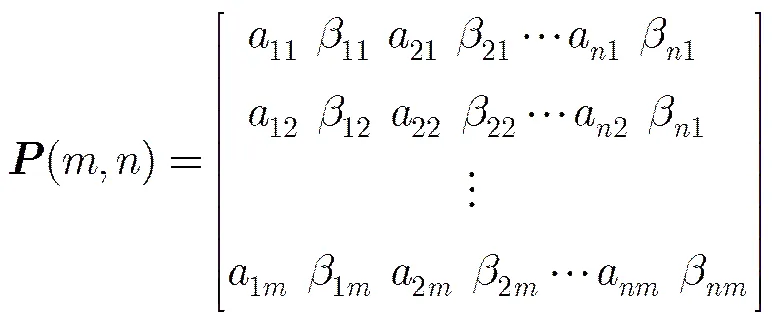
(19)

基于上述基因种群及适应度函数的定义，对第2节阵列天线进行遗传算法操作，最后得到合成方向图如图7所示，其中实线为目标方向图，虚线为合成方向图。由图7可见，合成方向图的副瓣抑制约。

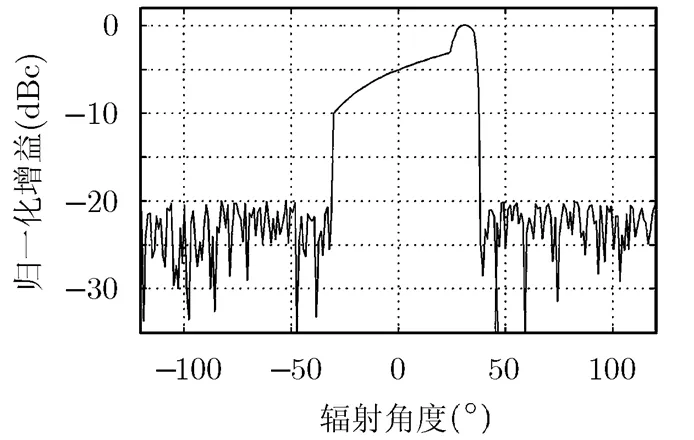
图6 目标方向图

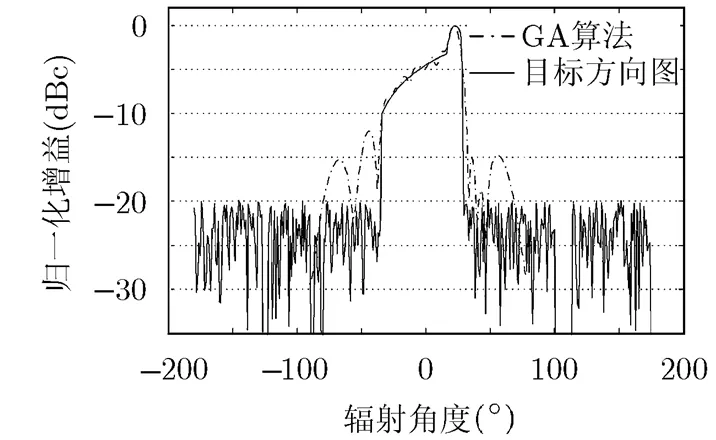
图7 合成方向图与目标方向图对比

6.2 基于低副瓣基波束的余割平方赋形波束设计流程

如图8所示，为低副瓣余割平方波束赋形的遗传算法设计流程，基于对基波束线性加权叠加而成。

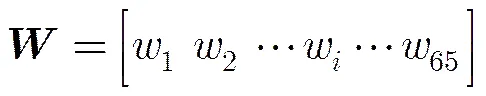
(22)

(23)

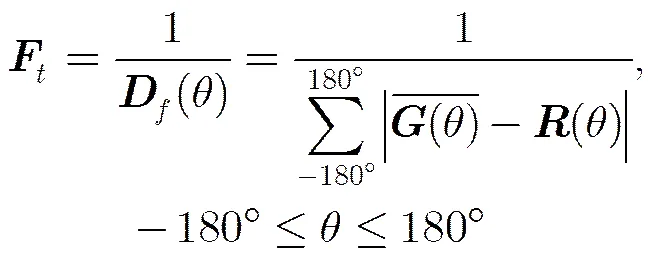
表1 激励求解结果

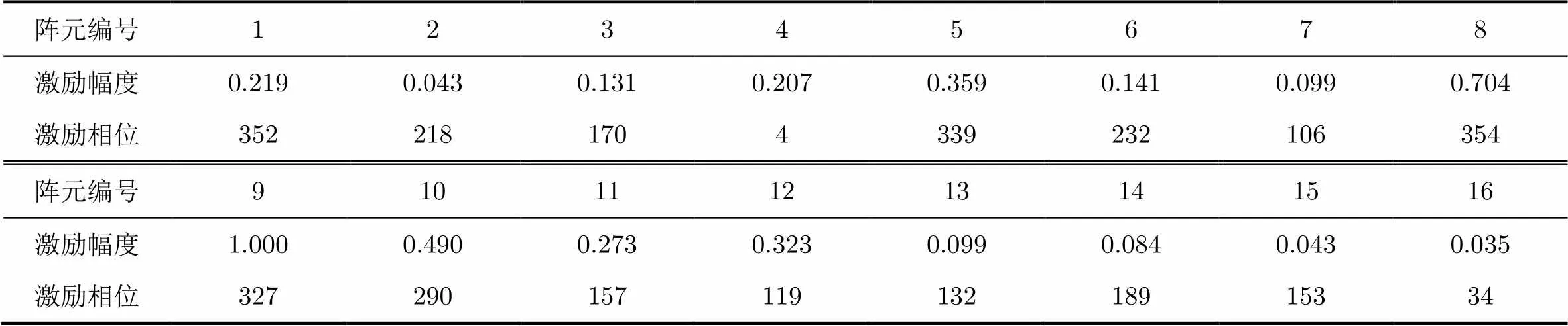
阵元编号12345678 激励幅度0.2190.0430.1310.2070.3590.1410.0990.704 激励相位3522181704339232106354 阵元编号910111213141516 激励幅度1.0000.4900.2730.3230.0990.0840.0430.035 激励相位32729015711913218915334

6.3 算法运算量对比

对比两种算法流程，相同之处包括：(1)方向图的加权叠加过程(记这个加权叠加过程为一次“加权叠加”)；(2)将合成方向图与目标方向图对比计算适应度；(3)选择、交叉、变异3个遗传过程；(4)判断新一代是否满足设计要求；这些过程贯穿真个算法循环，以3000代遗传为例，两种算法基本一致。

区别体现在：(1)方向图加权叠加的基础方向图有区别，传统遗传算法对阵元方向图进行矢量加权叠加，而本文改进的遗传算法，是对一种低副瓣的基波束进行加权叠加，因此在新的遗传算法开始前，需获得一组基波束，以文本的65个基波束获得过程为例，每个基波束获取过程与上述“加权叠加”，运算量相当。(2)本文提出的遗传算法在获得赋形结果后，需对65组幅相矩阵进行1次矩阵变化，求得实际阵列天线的激励矩阵，运算量和“加权叠加”的运算量相当。

因此，该文提出的遗传算法在运算量上，仅比传统遗传算法多出次“加权叠加”过程，且每次“加权叠加”运算位于一次遗传操作流程内，所以“加权叠加”的运算量小于一次遗传操作的运算量。以遗传算法3000次遗传过程为例，本文提出的新的遗传算法运算量为次遗传操作。最终，本文提出的遗传算法比传统遗传算法运算量增加值不大于。

7 结论

本文在阵列天线低副瓣波束扫描研究的基础上，提出了一种基于一组低副瓣波束线性叠加的波束合成机制，使合成方向图具有高副瓣抑制的特征，推导了合成方向图对应的阵元激励矩阵求解方法。进而将合成方向图与目标方向图做相似对比，基于遗传算法的基因优化方法，经过多次运算，获得与目标方向图匹配的合成方向图。以一款16阵元X波段微带偶极子线性阵列天线为例，本文提出的具有副瓣抑制机制的遗传算法求得的赋形波束获得了-27.5 dBc的副瓣抑制效果，远远好于文献[16]传统遗传算法求得的-19 dBc的副瓣抑制。值得说明的是，这种副瓣抑制机制是在遗传算法开始之初进行的独立设置，对算法在解空间选优特征无任何限制，因此可以预见这种机制对其他波束赋形算法的副瓣抑制也能起到一定的参考意义。

[1] MILIJIĆ M, NEŠIĆ A D, and MILOVANOVIĆ B. Design, realization, and measurements of a corner reflector printed antenna array with cosecant squared-shaped beam pattern[J]., 2016, 15: 421-424. doi:10.1109/LAWP.2015.2449257.

[2] HE Muxin, HAOZhangcheng, and FAN Kuikui. A planar millimeter-wave antenna with a cosecant squared pattern[C]. 2015 Asia-Pacific Microwave Conference (APMC), Nanjing, China, 2015: 1-3.

[3] SCATTONE F, ETTORRE M, SAULEAU R,. Generation of a cosecant-squared radiation pattern with a supersaturate-like leaky-wave antenna[C]. 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 2015: 1-4.

[4] MILIJIĆ M, NEŠIĆ A D, MILOVANOVIĆ B,. Wideband printed antenna array in corner reflector with cosecant square-shaped beam pattern[C]. 2014 22nd Telecommunications Forum Telfor (TELFOR), Belgrade, Serbia, 2014: 780-783.

[5] 赵菲, 齐会颖, 邱磊, 等. 自适应动态Meta粒子群优化算法综合多方向图共形阵列[J]. 电子与信息学报, 2012, 34(6): 1476-1482. doi: 10.3724/SP.J.1146.2011.01187.

ZHAO Fei, QI Huiying,QIU Lei,. Adaptive dynamic meta particle swarm optimization algorithm synthesizing multiple-pattern conformal array[J].&, 2012,34(6): 1476-1482. doi: 10.3724/SP.J.1146.2011.01187.

[6] ABDOLAHI M, ASKARI G, SADEGHI H M,. A new microstrip array antenna with cosecant-squared beam shaping as a radiating column for SSR[C]. 2014 22nd Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2014: 1781-1785.

[7] WANG Peng and YAO Zhiwen. Wave beam control design for VM-based phased array antenna[C]. Proceedings of 2011 International Conference on Electronics and Optoelectronics, Dalian, China, 2011: V2-22-V2-25.

[8] OLIVERI G, VIANI F, ANSELMI N,. Synthesis of multilayer WAIM coatings for planar-phased arrays within the system-by-design framework[J].,2015, Vol. 63: 2482-2496.

[9] TANHA M, BRENNAN P, ASH M,. Phased array antenna for avalanche FMCW radar[C]. Antennas and Propagation Conference (LAPC), Loughborough, England, 2013: 51-55.

[10] TSUTSUMI H, KUWAHARA Y, and KAMO H. Design of the series fed microstrip patch planar array antenna by the para to genetic algorithm[R]. 2015 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 2015: 1854-1855.

[11] CIORNEI I and KYRIAKIDES E. Hybrid ant colony-genetic algorithm (GAAPI) for global continuous optimization[J].,,,(), 2012, 42(1): 234-245. doi:10.1109/TSMCB.2011.2164245.

[12] CHÂARI I, KOUBÂA A, BENNACEUR H,. A hybrid ACO-GA algorithm for robot path planning[C]. 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 2012: 1-8.

[13] WEI Juan and WANG Ping. Optimization of fuzzy rule based on adaptive genetic algorithm and ant colony algorithm[C]. 2012 Fourth International Conference on Computational and Information Sciences, Chengdu, China, 2010: 359-362.

[14] KUNDUKULAM S and BEENAMOLE K. Design of a linear array antenna for shaped beam using genetic algorithm[J].-, 2008, 18(5): 410-416.

[15] UESAKA T and ARAI H. Design of cosecant squared beam collinear array using genetic algorithm[C]. 2013 IEEE International Workshop on Electromagnetics, Applications and Student Innovation Competition, Kowloon, Hong Kong, China, 2013: 74-75.

[16] DEHGHANI M, KARBALAEE Z, and MAHZON M. Design of a wide band antenna array with cosecant square pattern using genetic algorithm[C]. 2012 20th Telecommunications Forum (TELFOR), Belgrade, Serbia, 2012: 564-567.

Research on Genetic Algorithm of Antenna Arrays Beam Shaping with Side Lobe Suppression

ZHENG Zhanqi①YAN Yuepeng①ZHANG Lijun①WANG Yuhao①ZHANG Jinling②MU Fuqi①

①(,,100029,)②(,,100876,)

Excitation optimization algorithm based on Genetic Algorithm (GA) is mainly used to solve the excitation problems of array antenna beam shaping. When optimizing the excitation of array antenna by traditional genetic algorithm, the beam of array antenna is synthesized by radiation shape of elements in antenna array, and then the results will be compared with the target pattern. After several operations, the excitation will meet the deign requirements. However, in traditional genetic algorithm, neglected suppression of side lobe leads to an unsatisfactory high level side lobe. In this paper, a new method of beam synthesizing by peak beam of array antenna is proposed. By comparing the shape of synthesized beam with target beam and combining with traditional GA, the synthesized beam matching the target beam with low side lobe will be obtained. Taking a 16 elements X band micro-trip dipole linear array antenna as an example, the results of simulation show that array antenna has high level side lobe suppression at about -27.5 dBc using the method proposed in this paper, which is much better than -19 dBc side lobe suppression using traditional GA.

Antenna arrays; Genetic Algorithm (GA); Side lobe suppression

TN820

A

1009-5896(2017)03-0690-07

10.11999/JEIT160466

2016-05-09；改回日期：2016-12-07；

2017-01-11

郑占旗 zhengzhanqi@ime.ac.cn

郑占旗： 男，1982年生，助理研究员，主要研究方向为电磁场与微波技术、阵列天线设计、微波模块与系统设计.

阎跃鹏： 男，1964年生，研究员，主要从事卫星导航通讯、射频微波技术与电子系统总体设计研究.

张立军： 男，1963年生，研究员，主要从事雷达系统、射频微波技术与国防电子系统总体设计.

王宇灏： 男，1983年生，博士，主要从事雷达系统方向的研究.

张金玲： 女，1968年生，教授，主要从事电磁场与微波技术、生物医学电子学领域的研究.

慕福奇： 男，1960年生，研究员，主要从事通信系统、无线自组网技术与国防电子系统总体技术研究.