基于粒子滤波和滑动平均扩展Kalman滤波的多径估计算法

程兰王志远陈杰谢刚



基于粒子滤波和滑动平均扩展Kalman滤波的多径估计算法

程 兰*①王志远①陈 杰②谢 刚①

①(太原理工大学信息工程学院自动化系 太原 030024)②(北京理工大学复杂系统智能控制与决策国家重点实验室 北京 100081)

多径干扰是高精度定位的主要误差源，估计多径参数对消除多径误差，提高导航系统定位精度具有重要意义。针对扩展Kalman滤波(EKF)在进行多径参数估计时，存在对初值敏感，估计结果在真值附近具有较大波动的缺点，该文提出一种基于粒子滤波(PF)和滑动平均EKF的多径估计算法。该算法首先利用PF得到多径参数的粗略估计值，并将该值作为EKF的初始估计值，以克服EKF对初值敏感的问题。接着对EKF的估计结果进行滑动平均，并将平均后的滤波结果作为多径参数的估计结果。仿真结果表明，改进后的多径估计算法可有效降低估计结果的波动幅度，同时解决了EKF对初值敏感的问题。

参数估计；粒子滤波；扩展Kalman滤波；多径干扰

1 引言

多径干扰是高精度定位系统中的主要误差源[1,2]。多径存在时，接收机跟踪由直接信号和多径信号构成的复合信号，而我们期望接收机只跟踪直接信号，多径信号的存在使跟踪精度降低，进而带来了测距偏差，导致定位精度降低。多径误差受测量环境的影响具有很大的不确定性和不相关性，不能像电离层误差、对流层误差那样，通过差分技术消除[3]，因此，多径误差抑制成了导航系统高精度定位中的研究难点。

随着数字信号处理器的发展，基于数据处理的多径误差抑制方法成为近年来研究的热点[4]。基于数据处理的多径误差抑制方法的核心是参数估计，即首先根据接收信号(或相关输出)利用各种参数估计算法估计多径参数，并根据所估计的多径参数重构多径信号(或多径信号的相关输出)，然后从接收信号(或者接收信号的相关输出中)减去多径信号(或多径信号的相关输出)，得到直接信号的相关输出，再进行后续的跟踪处理等[4]。在基于数据处理的多径误差抑制方法中，基于扩展Kalman滤波(Extended Kalman Filter, EKF)的多径误差抑制方法是一种常用的方法[5,6]。然而，EKF能否收敛到正确值与初值直接相关，即EKF对初值敏感。而目前在基于EKF的应用中对初值的设置一般都设定为真值。在一般的跟踪系统中，系统状态的初值可以确定为真值[8]，而在基于EKF的多径估计中，我们往往很难获取多径参数的初值，文献[9]也已通过仿真分析证明了多径参数的初值对估计结果具有较大的影响，偏差较大的初值可能导致多径估计结果收敛到错误值、甚至发散，从而无法实现抑制多径误差的目的。

同时，EKF算法需要对非线性方程进行线性化带来了截断误差，致使EKF算法的估计结果具有较大的波动[10]。为了克服EKF的这个固有缺点，研究者提出了几种改进算法，如二阶EKF、迭代EKF、修正增益EKF以及修正协方差EKF[11]。然而，二阶EKF的运算开销随着状态维数增加而显著增大、迭代EKF必须以高精度观测为前提，修正增益EKF以及修正协方差EKF的修正矩阵不存在或难推导。因此，这些改进算法在解决实时性要求较高、噪声强度大的导航系统中的多径估计问题时，往往还不如EKF快速、直接。

近年来，迅速发展的粒子滤波(Particle Filter, PF)因其不需要对观测方程线性化，对噪声不敏感等优点，被广泛应用于目标跟踪、故障诊断、人脸识别等领域中。PF利用先验信息产生初始粒子群，并利用贝叶斯准则进行参数的后验估计[12]。PF对初始粒子的选择具有较大的随机性，且不同的初始粒子对估计结果的影响并不明显，这一优点正是本文在解决EKF初值敏感问题时所要借鉴的。但PF需要对多个粒子进行贝叶斯估计，相比于只需要一个粒子就能进行状态估计的EKF，其时间复杂度大大增加。而且，在高斯噪声下PF的估计性能明显低于EKF的估计性能。

因此，为了既利用PF对初值不敏感的优点，又可以降低多径估计算法的时间复杂度，本文利用PF进行初始估计，将PF的估计结果作为EKF的估计初值，然后利用EKF进行后续估计。同时，为了解决EKF的估计结果在真值附近具有较大波动的问题，本文采用对EKF的滤波结果进行滑动平均的方法对当前时刻的估计结果进行平滑处理，可以有效降低估计结果的波动幅度。

2 问题描述

2.1 信号模型

多径信号存在时，GPS接收机的基带信号模型可建模为[13]

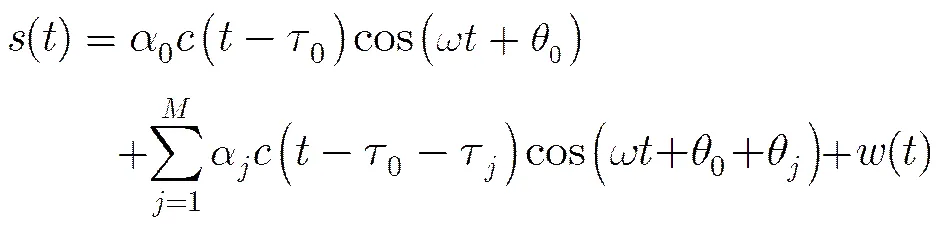
上述模型忽略了数据码的影响。其中，第1项表示直接信号，第2项表示路多径信号；为直接信号的幅值；()为调制在载波上的C/A码；为直接信号的伪码延时；为多路径的个数；为第路多径信号的幅值，为第个多径信号相对于直接信号的时间延迟；多径信号的时间延迟只考虑小于一个码片的情况(超过一个码片的多径信号对跟踪环的影响很小)，为基带信号载波频率，是加性高斯白噪声。

对接收信号进行数字化，模型式(1)可表示为

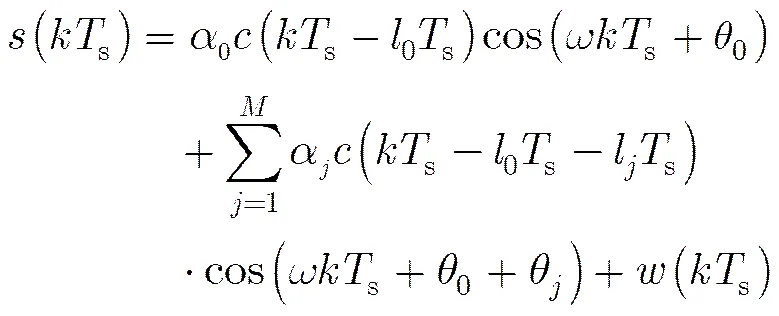
接收信号与本地伪码进行相关运算，得到的相关输出为

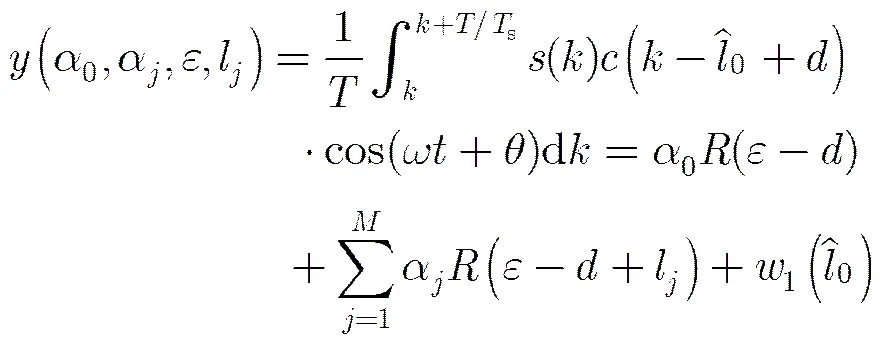
式中，

2.2 多径估计结构

3 基于PF和滑动平均EKF的多径估计算法

3.1 多径估计问题的状态空间模型

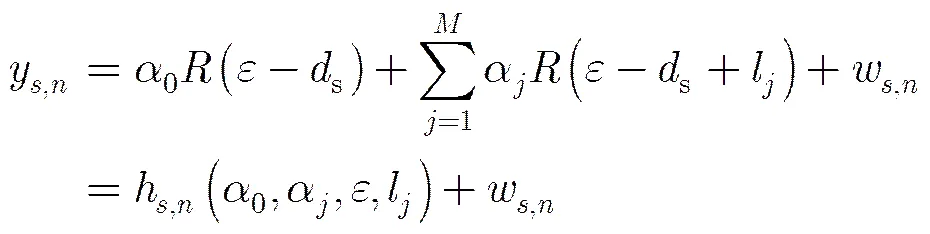
状态模型：(5)

观测模型：(6)

图1 基于PF和滑动平均EKF的多径估计结构

3.2 算法基本原理

首先根据多径参数的先验信息产生PF的初始种群，并进行PF滤波，当PF滤波结果趋于稳定时，将滤波结果作为EKF的初值，并切换到EKF模式。在EKF模式下，采用滑动平均的方式降低估计偏差对滤波输出的影响。具体的算法流程如图2所示。

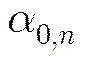
(7)

(8)

(10)

(2)基于PF的多径估计：产生初始种群后，就可以根据PF进行滤波估计。PF是一种基于蒙特卡罗方法和递推贝叶斯估计的统计滤波方法，是贝叶斯滤波的一种近似解。它通过一组从重要性密度函数(·)中采样的随机样本和与之对应的权重来近似后验概率密度函数，,为粒子个数[12]。在滤波过程中为避免出现样本枯竭，需要进行重采样。

图2 基于PF和滑动平均EKF的多径估计算法

PF算法基本流程：

(a)根据先验分布产生随机样本，即

新算法在进行迭代过程中，前次迭代用PF估计多径参数并输出估计结果。当估计结果开始收敛时，就把此时刻的参数值作为EKF的初值继续进行后续的迭代估计。需要说明的是，在初始时刻样本是根据多径参数的取值范围由均匀分布来产生初始种群，而在PF的迭代过程中，用预测分布来代替重要性分布函数以降低权值的计算复杂度，这种重要性函数选择方案也是PF算法的一般选择方案[12]。本文采用的重要性分布函数为高斯分布，具有如下形式：，其中为的维数，为时刻的第个粒子。为时刻的状态值预测值，为的预测估计协方差。和的计算可根据式(11)和式(12)得到。

(3)基于滑动平均EKF的多径估计：根据PF获得EKF的滤波初值后，即可切换到EKF模式下进行滤波估计。此时个粒子的滤波就变为只有一个粒子的EKF滤波，降低了时间复杂度。EKF的滤波过程可以描述如下：

(a)根据上一时刻的状态值预测当前时刻的状态估计值：

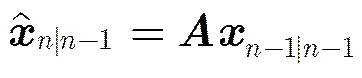
(b)误差协方差阵预测：

(12)

(c)计算观测矩阵：

(d)计算卡尔曼增益：

(14)

(e)根据真实观测值更新状态估计值：

(f)更新误差协方差阵：

(16)

在式(13)中需要对观测方程求偏导才能得出线性化的观测矩阵。为了简单，本文以单一多径，即为例，说明的计算过程。即。因此，根据式(13)可以求得线性化的观测矩阵，即

在计算观测矩阵时需要用到自相关函数的偏导数，假设()具有理想的自相关特性，则

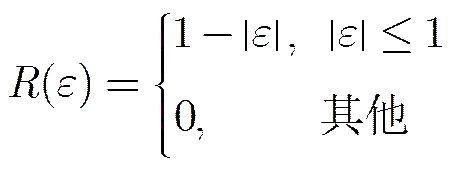
对自相关函数求偏导得：

(19)

为了降低EKF估计结果的波动幅度，在静态环境中，可通过滑动平均的方法对滤波结果进行平滑处理，以降低多径估计结果的波动幅度。假设滑动窗的长度为，则基于滑动窗的平滑处理结果可表示为

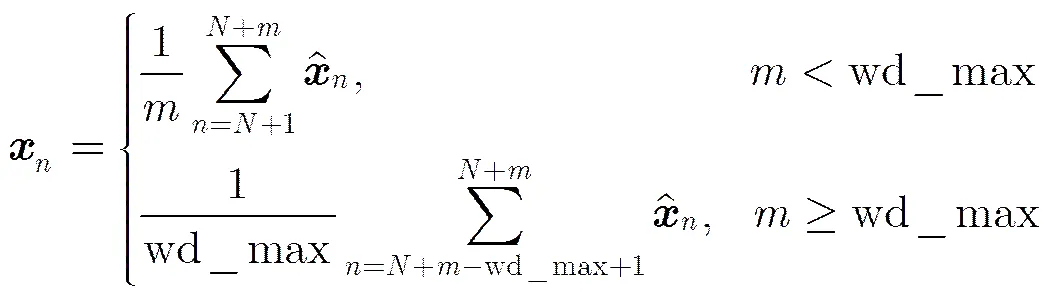
3.3 算法实现

基于PF和滑动平均EKF的多径估计算法实现如表1所示。在算法实现过程中，决策判决是通过判断PF的滤波次数是否达到来实现的。当PF的滤波次数小于时，输出PF的滤波结果(for1循环)；当滤波次数等于时，将PF的滤波结果作为EKF的初值，并切换到滑动EKF模式(for2循环)。可以看出，参数决定了PF和EKF的切换时刻，因此需要对进行选择，本文通过仿真实验来确定，即刚开始只采用PF进行多次仿真，找到可以保证PF收敛的迭代次数作为。在本文考虑的情况中，选择可以保证PF收敛。同理，在滑动平均EKF中，需要对进行选择。本文中也是通过仿真来确定的，在确定时需要兼顾计算复杂度和精度，太小无法达到平滑的效果，导致估计精度不能满足要求，而太大又会增加计算复杂度，且较大的对估计结果的平滑程度改进并不明显，因此，本文通过逐渐增大来观测估计结果的改善程度，以选择合适的。

3.4 算法复杂度分析

与EKF相比，本文算法在前个时刻采用PF进行参数估计，其时间复杂度实际上是PF滤波的时间复杂度，这也是本文算法最耗时的阶段。因为PF需要对p个粒子进行贝叶斯估计才能获得状态的后验估计，即时间复杂度为，也就是说PF的复杂度随粒子数目增加线性增加。而EKF只需要对1个粒子进行估计，其时间复杂度为O(1)。在时刻之后，本文算法实际就是EKF算法，只需要保存个状态估计结果，用于滑动平均计算。滑动平均计算仅涉及(wd_max+1)次加法和1次乘法运算。所以，本文算法复杂度介于PF和EKF之间。为了更加直观地比较本文算法的时间复杂度，我们在一台索尼笔记本电脑上进行了时间复杂度对比分析。实际复杂度计算采用了100次蒙特卡罗仿真，并取平均值，并设,,,。EKF算法迭代1次需要0.13 ms，本文算法需要0.20 ms。

考虑接收机在不同应用场合下的实时性要求。如，对于以时速120 km/h(33.3 m/s)的速度行驶的汽车而言，要想达到2 m左右的定位精度，算法的1次迭代时间不应超过60 ms。而本文算法的1次平均迭代时间仅需0.20 ms，所以所提出算法可以满足这种情况下的定位需求。

表1 基于PF和滑动平均EKF的多径估计算法伪码

4 仿真分析

本次仿真只考虑了单一多径的情况，这是因为尽管理论上多径信号的个数可能是多个，但实际上在某一时刻通常只有一路或两路多径信号起决定性作用[14]。且文献[14]中也提到考虑多于1路的多径信号对多径抑制性能的改善并不十分显著，所以本文只考虑了单一多径。仿真采用2号卫星的C/A码，采样倍数s=10，状态真值0=[0.5, 0.7, 0.2, 0.4]T,=diag([0.0001, 0.0001, 0.0001, 0.0001])，信噪比SNR =-20 dB，通过7路相关输出获得测量数据，即早码侧和晚码侧各有3路相关器，并且关于即时码对称，各支路与及时码的相关间距为(= 1, 2,, 7)分别取值,,, 0, -, -, -。其中表示早码支路，则表示晚码支路，表示即时码支路。相关输出支路数与待估参数的维数相关，即相关输出的支路数应大于待估参数的维数。仿真结果如图3所示。

在图3的仿真中将真值0作为EKF的初始值，而新算法通过PF来预测初值。其中PF的初始粒子根据式(7)~式(10)产生个服从均匀分布的初始粒子，通常选为待估参数维数的10倍，因此，当考虑单一多径时，有4个待估参数，所以PF的粒子数目选为，若考虑多路多径参数时可据此原则增加初始粒子数目。从图3中可以看出，本文算法的多径估计性能明显优于EKF和PF算法，出现较小的波动幅度，而EKF由于受到观测方程线性化误差的影响，导致估计值围绕真值具有较大的波动。而PF的波动幅度比EKF更大，这是因为PF只采用先验概率密度函数产生初始种群，并未考虑当前测量输出中包含的信息。同时，从图3也可以看出，本文算法在刚开始的前次迭代中也出现了波动现象，这是因为前次的滤波结果为PF的滤波结果，此后开始利用滑动平均的方法来平滑EKF的滤波结果，可以根据需要调整。

图3的仿真中，EKF的初值为真值，所以EKF的估计结果虽然具有较大波动，但仍可收敛到真值附近。为了说明新算法可以克服EKF对初值敏感的问题，我们进行了第2组仿真，仿真结果如图4所示。本次仿真将EKF的初值设置为根据先验信息获得一个随机值，新算法仍根据第1组仿真的方法随机产生p个初始粒子。经过多次仿真发现，EKF对状态初值比较敏感，当EKF的初始值偏离真值较小时，估计参数的收敛速度降低，当EKF的初始值偏离真值较大时，会收敛到错误的值，甚至发散，而新算法估计结果始终是收敛的，克服了EKF 对初值敏感的问题。

对PF, EKF，本文算法从对初值是否敏感、计算复杂度、估计精度以及估计结果的波动幅度几个方面进行比较，结果如表2所示，综合来说，3种算法中，本文算法具有最好的性能。

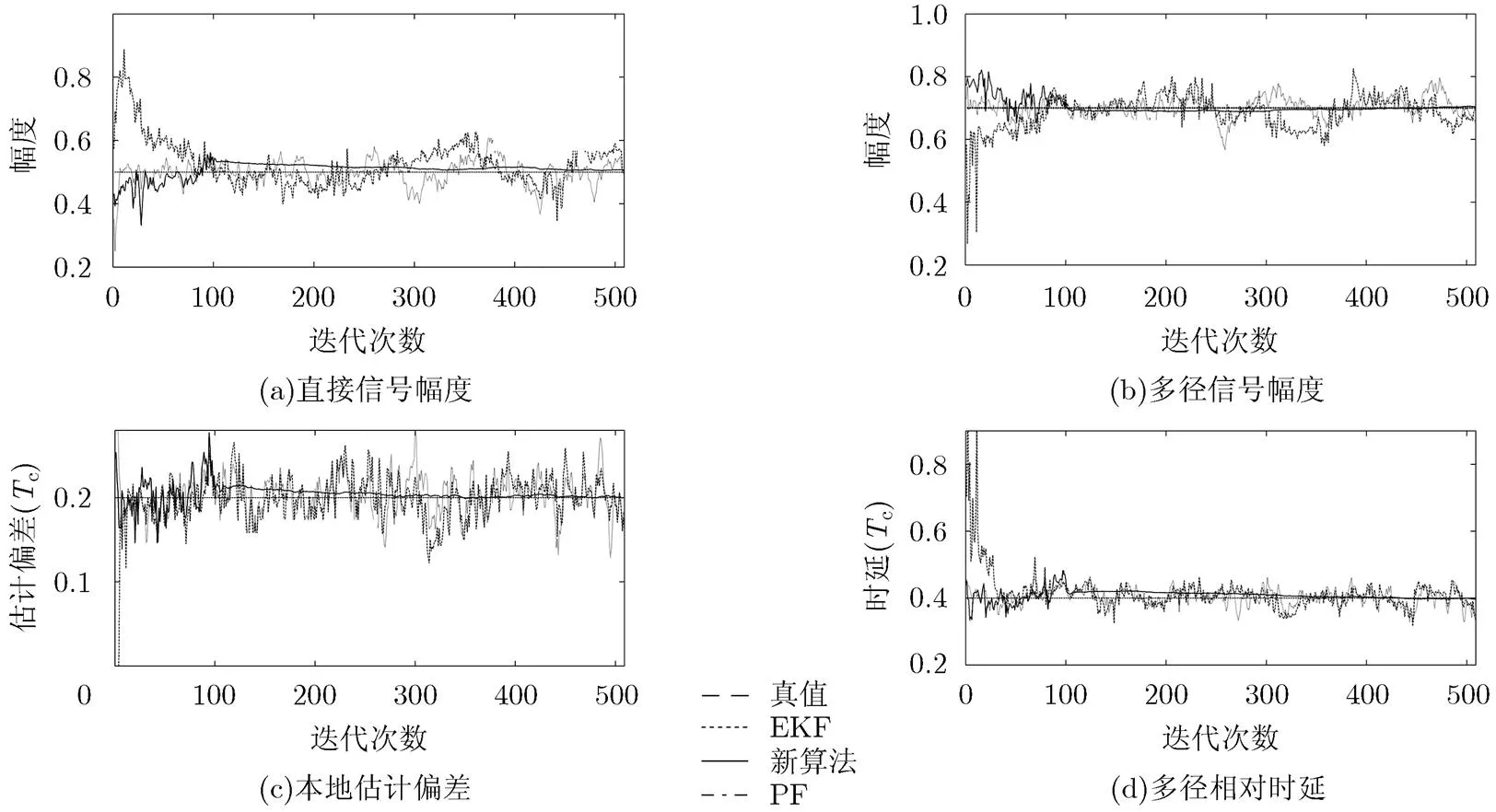
图3 EKF的初值为真值时的估计结果

表2 PF、EKF与本文算法的对比结果

图4 EKF的初值为随机数时的一次估计结果

5 结束语

本文针对基于EKF的多径估计算法存在对初值敏感，且多径估计结果围绕真值具有较大波动的问题，提出了一种基于PF和滑动平均EKF的多径估计算法。该算法利用了PF对状态初值不敏感的优点，将其估计结果作为EKF的估计初值，克服了EKF因初值设置不合理而导致估计结果收敛到错误值或者发散的问题。同时，利用了EKF估计的状态后验概率密度函数为高斯分布的特点，采用滑动平均的方法对EKF的估计结果进行平滑处理，以降低估计结果的波动性。仿真结果验证了算法的有效性。本文主要完成了算法的仿真验证，在后续工作中我们将考虑用实际信号验证算法的有效性。

[1] BRAASCH M S and BIBENEDETTO M F. Spread- spectrum ranging multipath model validation[J]., 2001, 37(1): 298-304. doi:10.1109/7.913691.

[2] 程兰, 陈杰, 甘明刚. GPS接收机载波跟踪多径误差分析[C].第29届中国控制会议论文集, 北京, 2010: 573-576.

CHENG Lan, CHEN Jie, and GAN Minggang. Multipath error analysis of carrier tracking loop in GPS receiver[C].Proceedings of the 29th Chinese Control Conference, Beijing, 2010: 573-576.

[3] 张孟阳, 吕保维, 宋文淼. GPS系统中的多径效应分析[J]. 电子学报, 1998, 26(3): 10-14.

ZHANG Mengyang, LÜ Baowei, and SONG Wenmiao. Analyses of multipath effects in the GPS system[J]., 1998, 26(3): 10-14.

[4] 程兰, 陈杰, 谢刚. 软件接收机中基于数据处理的多径估计方法[J]. 系统工程与电子技术, 2013, 35(10): 2050-2056. doi: 10.3969/j.issn.1001-506X.2013.10.06.

CHENG Lan, CHEN Jie, and XIE Gang. Multipath estimation algorithms based on data processing in soft ware receiver[J]., 2013, 35(10): 2050-2056. doi: 10.3969/j.issn.1001-506X.2013.10.06.

[5] 张文明, 周一宇, 姜文利. 基于扩展卡尔曼滤波的GPS多径抑制技术[J]. 宇航学报, 2003, 24(1): 53-56. doi: 10.3321/ j.issn:1000-1328.2003.01.010.

ZHANG Wenming, ZHOU Yiyu, and JIANG Wenli. GPS multipath rejection through EKF[J]., 2003, 24(1): 53-56.doi: 10.3321/j.issn:1000-1328.2003.01.010.

[6] ILTIS R A. Joint estimation of PN code delay and multipath using the extend kalman filter[J]., 1990, 38(10): 1677-1685.

[7] 熊伟, 陈立奎, 何友, 等. 有色噪声下的不敏卡尔曼滤波器[J]. 电子与信息学报, 2007, 29(3): 598-600.

XIONG Wei, CHEN Likui, HE You,. Unscented Kalman filter with colored noise[J].&, 2007, 29(3): 598-600.

[8] 黄小平, 王岩石. 卡尔曼滤波原理及应用[M]. 北京: 电子工业出版社, 2015: 89-90.

HUANG Xiaoping and WANG Yanshi. Kalman Filter and Its Application[M]. Beijing: Publishing House of Electronics Industry, 2015: 89-90.

[9] 程兰, 谢刚. 一种基于扩展Kalman滤波的多径估计算法[J]. 太原理工大学学报, 2012, 43(5): 575-579.doi: 10.3969/j.issn.1007-9432.2012.05.011.

CHENG Lan and XIE Gang. A multipath estimation algorithm based on extended Kalman filter[J]., 2012, 43(5): 575-579. doi: 10.3969/j.issn.1007-9432.2012.05.011.

[10] 程兰. 软件接收机原理及多径误差研究[M]. 北京: 国防工业出版社, 2015: 170-182.

CHENG Lan. Software Receiver Principle and the Research of Multipath Error[M]. Beijing: China National Defence Industry Press, 2015: 170-182.

[11] 占荣辉, 张军, 欧建平, 等. 非线性滤波理论与目标跟踪应用[M]. 北京: 国防工业出版社, 2013: 43-46.

ZHAN Ronghui, ZHANG Jun, OU Jianping. Nonlinear Filtering Theory with Target Tracking Application[M]. Beijing: China National Defence Industry Press, 2013: 43-46.

[12] 朱志宇. 粒子滤波算法及其应用[M]. 北京: 科学出版社, 2010: 27-32.

ZHU Zhiyu. Particle Filter and Its Application[M]. Beijing: Science Press, 2010: 27-32.

[13] CHENG Lan, CHEN Jie, and XIE Gang. Model and simulation of multipath error in DLL for GPS receiver[J]., 2014, 23(3): 508-515.

[14] Townsend B R, Fenton P C, Dierendonck K J V,. Performance evaluation of the multipath estimating delay lock loop[J]., 1995, 42(3): 502-514. doi:10.1002/j.2161-4296.1995.tb01903.x.

An Improved Multipath Estimation Algorithm Using Particle Filter and Sliding Average Extended Kalman Filter

CHENG Lan①WANG Zhiyuan①CHEN Jie②XIE Gang①

①(,,030024,)②(,,100081,)

Multipath is the dominant error source for high-accuracy positioning systems. It is significant for eliminating the multipath error and improving the positioning accuracy to estimate multipath parameters. There are two main disadvantages for multipath parameters estimation by using the Extended Kalman Filter (EKF): it is sensitive to the initial value; filtering results fluctuate obviously around actual values. To solve these problems, an improved multipath estimation algorithm based on Particle Filter (PF) and sliding average EKF is proposed. Firstly, PF is used to obtain rough estimation values of multipath parameters, which are set as initial estimations for EKF to reduce the initial value sensitivity. Then, the EKF filtering results are smoothed by sliding average. The smoothing results are outputted as the multipath estimation. The simulation results show that the estimation results of the proposed algorithm have smaller fluctuation magnitude compared with EKF, and it is insensitive to the initial estimation.

Parameter estimation; Particle Filter (PF); Extended Kalman Filter (EKF); Multipath interference

TN966; TP273.1

A

1009-5896(2017)03-0709-08

10.11999/JEIT160587

2016-06-03；改回日期：2016-11-11；

2017-01-22

程兰 taolan_1983@126.com

国家自然科学基金(61503271, 61603267)，山西省自然科学基金(20140210022-7)，复杂系统智能控制与决策国家重点实验室开放基金(900101-03910353)

The National Natural Science Foundation of China (61503271, 61603267), The Natural Science Foundation of Shanxi Province (20140210022-7), The Open Foundation of Key Laboratory of Intelligent Control and Decision of Complex Systems (900101-03910353)

程 兰： 女，1984年生，讲师，博士，主要研究方向为导航系统高精度定位、信号跟踪.

王志远： 男，1989年生，硕士生，研究方向为导航系统高精度定位、多径抑制等.

陈 杰： 男，1965年生，教授，博士，主要研究方向为智能控制与智能系统、多目标优化与决策、非线性控制等.

谢 刚： 男，1972年生，教授，博士，主要研究方向为智能信息处理、智能控制等.