基于优化理论的复杂网络节点攻击策略

孙 昱 姚佩阳 张杰勇 付 凯



基于优化理论的复杂网络节点攻击策略

孙 昱*姚佩阳 张杰勇 付 凯

(空军工程大学信息与导航学院 西安 710077)

该文在分析传统复杂网络节点攻击策略不足的基础上提出一种新的攻击策略，该策略的思路是将节点攻击序列的构造问题视为一个优化问题而非传统的评估问题。为了实现该策略，设计了复杂网络抗毁性测度用以衡量节点攻击序列的攻击效果，建立了以最大化攻击效果为目标的节点攻击序列构造模型，提出了基于禁忌搜索的模型求解算法。在真实网络和模拟网络上的实验结果表明，新策略比其它复杂网络节点攻击策略更为有效和优越。

复杂网络；攻击策略；抗毁性测度；优化模型；禁忌搜索

1 引言

复杂网络节点攻击是通过破坏目标网络中的节点以使目标网络无法维持其基本功能的行为。在实施复杂网络节点攻击时，目标网络中的节点按被破坏的先后次序可以构成一个序列，该序列称为节点攻击序列。复杂网络节点攻击策略规定了节点攻击序列的构造方式，目的是使目标网络在节点攻击当中迅速崩溃。复杂网络攻击策略的发展有利于促进复杂网络防护策略的完善，因此研究更为有效的复杂网络节点攻击策略具有重要意义。

目前关于复杂网络节点攻击策略的研究已取得不少成果[1]。经典的节点攻击策略包括度优先攻击策略[2]和介数优先攻击策略[3]。为进一步提高这两种策略的攻击效果，文献[4]认为可以综合考虑节点的度大小及其第2邻居的数量来实施攻击。文献[5]分别给节点的度和介数赋予权重并选择二者加权和大的节点优先攻击。文献[6]则构造了双重判断准则，即先攻击度大的节点，当节点的度相同时，攻击其中介数大的节点。文献[7]提出了一种邻近攻击策略，其基本思想是若某个节点受到攻击，则其邻居节点接下来更可能被攻击。文献[8]从破坏复杂网络社团结构的角度出发，设计了一种针对高社团成员值节点的多靶向攻击策略。文献[9]和文献[10]分别定义了Damage指标和中心性指标以衡量节点在网络中的重要程度，然后优先攻击网络中重要程度高的节点。文献[11]认为通用的节点重要度指标难以准确定义，因此引入优化原理来设计最佳的节点攻击策略。

从目前的研究进展看，大部分节点攻击策略都是基于重要度的理念来构造节点攻击序列，即先选择节点的某种结构特征例如度、介数等作为其重要性度量，然后根据网络中各节点的重要程度将节点排序形成节点攻击序列。此类节点攻击策略往往各有优劣，这是因为复杂网络的结构多种多样(研究较多如随机网络、小世界网络、无标度网络，研究较少且未统一命名的网络类型更是不计其数)，很难找到某种结构特征在所有网络中都能较好地度量节点的重要性。文献[11]认识到这一点，尝试以优化的方式解决问题，不足之处是需要事先给出攻击强度等信息。

为了设计更为有效实用的复杂网络节点攻击策略，本文基于优化理论来构造节点攻击序列。首先给出衡量节点攻击序列攻击效果的测度指标，然后建立节点攻击序列构造的优化模型并提出可行的求解算法，最后对比不同攻击策略在真实网络和模拟网络上的攻击效果以验证新策略的有效性和优越性。

2 复杂网络抗毁性测度

复杂网络抗毁性测度用来衡量节点攻击序列的攻击效果。当事先构造一个节点攻击序列并按照中的节点排序逐个攻击网络中的节点时，随着攻击的进行，网络最大连通分量的规模将不断降低，因此网络在攻击序列下的抗毁性测度通常被定义为[12]

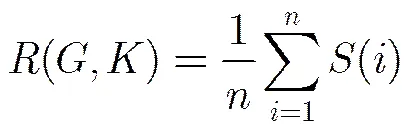
为了克服其不足，本文首先设计能在更为细致的粒度上反映网络整体连通状况的指标，然后在此基础上定义新的网络抗毁性测度。在一个网络中，若两个节点之间存在一条可达路径，则称这对节点是连通的。网络中连通的节点对数越多，网络的整体连通程度越好。若网络中共有个连通分量，第个连通分量包含的节点数为，则网络中连通节点对的数量为，考虑到网络中节点对的数量最多为(其中是中的节点总数)，因此定义网络的可用性指标为

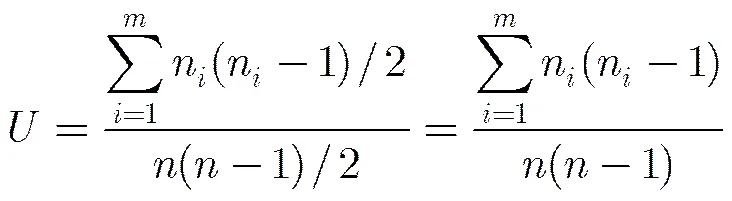
当网络中的节点遭受攻击而被移除出网络时，网络的可用性指标值不一定单调减少，如图1所示的网络中，若7号节点遭到攻击而被移除，网络的可用性指标值将由0.71变为1。网络受到了攻击其可用性反而更好了，这显然与人们的直觉认识不相符合，也为网络抗毁性测度的定义造成了困难。

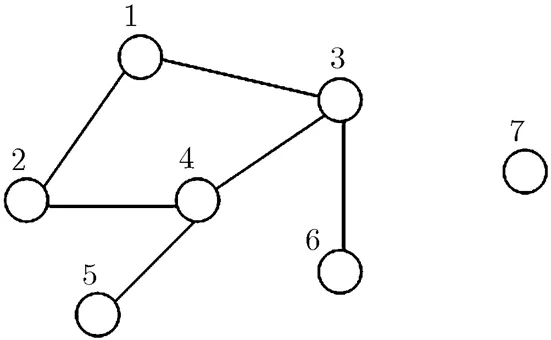
图1 网络示例图

由于将1个节点移除出网络在效果上等价于将连接到该节点的边都移除出网络，因此为了使网络可用性指标值随着攻击的进行而单调减少，作如下规定：当网络中节点被攻击时，并不将该节点移除出网络，而是将网络中连接到该节点的所有边都移除出网络。根据这一规定，当网络中的孤立节点如图1中的7号节点受到攻击时，网络可用性指标值将维持不变，当网络中的非孤立节点如图1中的1号节点至6号节点受到攻击时，网络可用性指标值将降低。

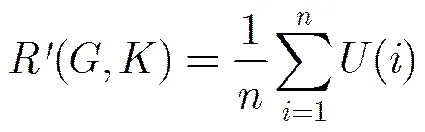
3 节点攻击序列构造

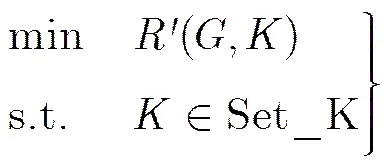
禁忌搜索是一种求解组合优化问题的有效算法[15]，具有参数少、通用性强等特点，其基本思想是从一个初始解出发，然后在其邻域中搜索较好的解并移动到该解，重复上述步骤直至算法满足终止准则，为了避免搜索过程陷入循环，设置禁忌列表来禁忌可能导致循环发生的搜索行为。本文首先基于禁忌搜索设计式(4)中所建模型的求解算法，然后进一步优化算法性能。

3.1 模型求解

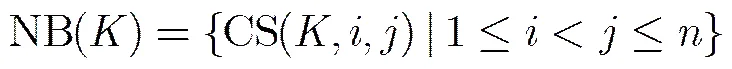
定义3 禁忌列表是用于记忆信息的一块存储区域，其每一个表项可以存储模型的一个解。

基于禁忌搜索的模型求解算法具体步骤如下：

3.2 性能优化

为了进一步提高求解算法的性能，本文从初始解构造和邻域搜索两个方面来优化算法。

(1)初始解构造： 较好的初始解有利于提高算法的收敛速度。求解算法在步骤1中通过随机的方式产生初始解难以保证初始解的质量，因此本文根据问题信息针对性地构造较好的初始解。在攻击一个网络时，攻击其核心节点比攻击边缘节点造成的破坏性更大，故可以先评价网络中各节点的中心性程度，然后再构造初始解。

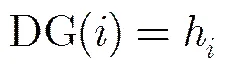
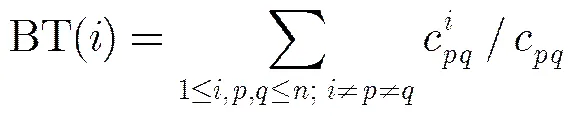
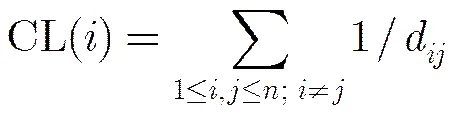
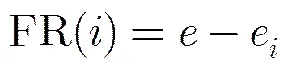
根据节点的中心性程度构造初始解的方式如下。选择一种节点中心性度量方式，计算网络中所有节点的中心性测度值，将中心性程度最高的节点作为节点攻击序列中的第1个目标，将该节点从网络中移除，重新计算剩余节点的中心性测度值，其中中心性程度最高者作为节点攻击序列中的第2个目标，重复上述步骤直至构造出一个完整的节点攻击序列。若各种中心性度量方式构造出的初始解不同，则在搜索时采取并行搜索思想为每个初始解开启一个搜索任务。

4 实验验证

本节通过实验证明所提复杂网络抗毁性测度的有效性以及节点攻击策略的优越性。本文实验平台为Pentium(R) Dual-Core CPU 3.0 GHz计算机和MATLAB R2010a。

仿真实验1 为对比式(1)中定义的传统复杂网络抗毁性测度和式(3)中定义的新复杂网络抗毁性测度，利用随机网络模型，小世界网络模型(重连概率为0.2)和无标度网络模型生成节点数为50，边数为100的模拟网络，采用经典的介数优先攻击策略和度数优先攻击策略攻击这些网络，各类型网络均进行30组实验，计算网络抗毁性测度的均值并进行归一化处理，结果如图2所示。

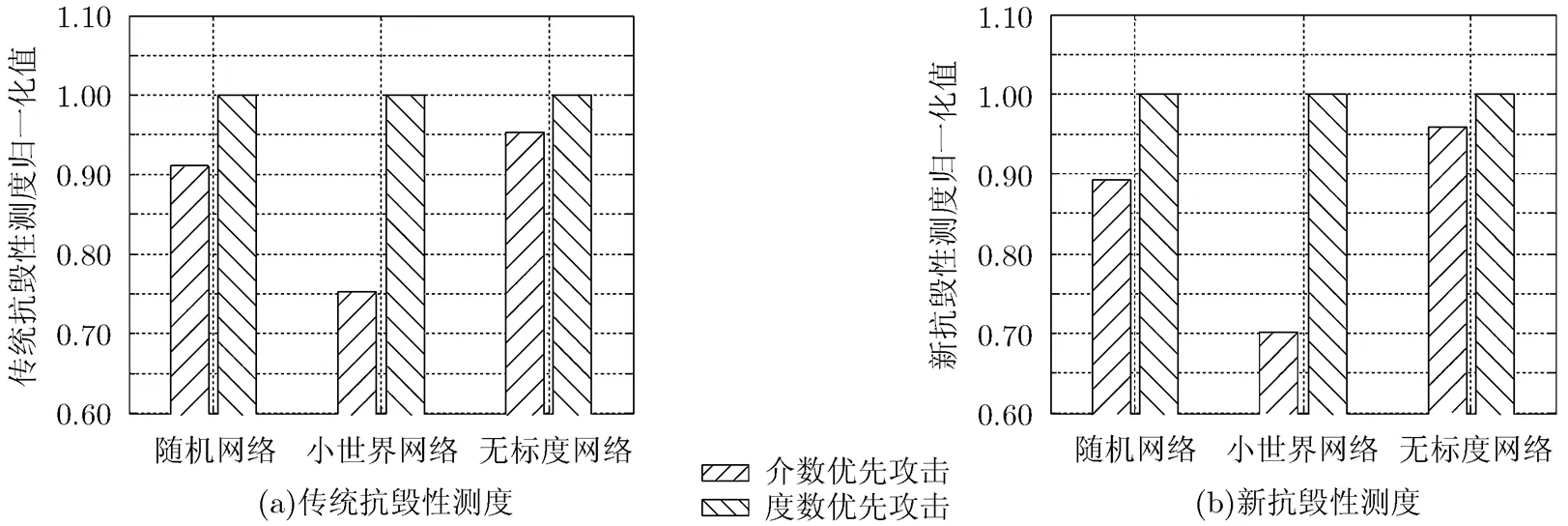
图2 复杂网络抗毁性测度对比

从图2中可以看到，介数优先策略的攻击效果要优于度数优先策略，在用传统抗毁性测度衡量时，介数优先策略在随机网络、小世界网络和无标度网络上的攻击效果要比度数优先策略分别优8.89%, 24.79%和4.65%，用新抗毁性测度衡量时，介数优先策略分别优10.69%, 29.79%和4.11%。新测度说明了介数优先策略在随机网络和小世界网络上的攻击效果比以往料想得要更为有效一些，而在无标度网络上的攻击效果要比以往料想得弱一些，这是因为在无标度网络这种节点度接近幂律分布的网络中，各攻击策略都能比较容易地确定其重要节点，因此攻击效果比较接近，而在随机网络和小世界网络这类节点度近似泊松分布的网络中，确定重要节点并不像在无标度网络中那么简单，此时介数优先策略作为全局性策略的攻击效果就比度数优先策略这种局部性策略更容易显现出来。图2中的实验结果表明新测度更加细致地刻画了网络的整体状态，因此该测度是可行有效的。

仿真实验2 为验证本文所提攻击策略的优越性，首先对比不同攻击策略在图3所示真实网络上的攻击效果，其中图3(a)是西安市莲湖区的城区道路网，图3(b)是中国教育和科研计算机网(CERNET)的主干网络。实验结果如图4所示。

从图4中可以看到，无论采用哪种攻击策略，随着受攻击节点数量的增加，网络的可用性都越来越差，横向对比这3种策略可以发现，本文提出的攻击策略能使网络的可用性指标值下降得更为迅速。由式(3)计算得到的城区道路网在本文攻击策略、介数攻击策略和度数攻击策略下的抗毁性测度值分别为0.1195, 0.1247, 0.1730, CERNET主干网在这3种攻击策略下的抗毁性测度值分别为0.0619, 0.0671, 0.0769，即本文所提策略在城区道路网上的攻击效果要比介数优先策略和度数优先策略分别优4.17%和30.92%，在CERNET主干网上的攻击效果分别优7.75%和19.51%。继续在模拟网络上进行验证，利用随机网络模型，小世界网络模型(重连概率为0.2)和无标度网络模型生成节点数为50，边数为100的模拟网络，计算模拟网络在不同攻击策略下的抗毁性测度，各类型网络均进行30组实验，结果如图5所示。

在图5中，本文攻击策略所得的数据分布相对于其它两种攻击策略而言总体偏低，其中随机网络在本文攻击策略、介数攻击策略和度数攻击策略下的抗毁性测度均值为0.1347, 0.1495, 0.1674，小世界网络在这3种攻击策略下的抗毁性测度均值为0.1300, 0.1390, 0.1980，无标度网络在这3种攻击策略下的抗毁性测度均值为0.1034, 0.1113, 0.1161，即本文所提策略在随机网络上的攻击效果比介数攻击策略和度数攻击策略分别优9.90%和19.53%，在小世界网络上的攻击效果分别优6.47%和34.34%，在无标度网络上的攻击效果分别优7.10%和10.94%。图4和图5中的实验结果表明本文攻击策略不仅优越，而且适用于不同类型的网络之中，这证明基于优化思想的节点攻击策略鲁棒、高效。

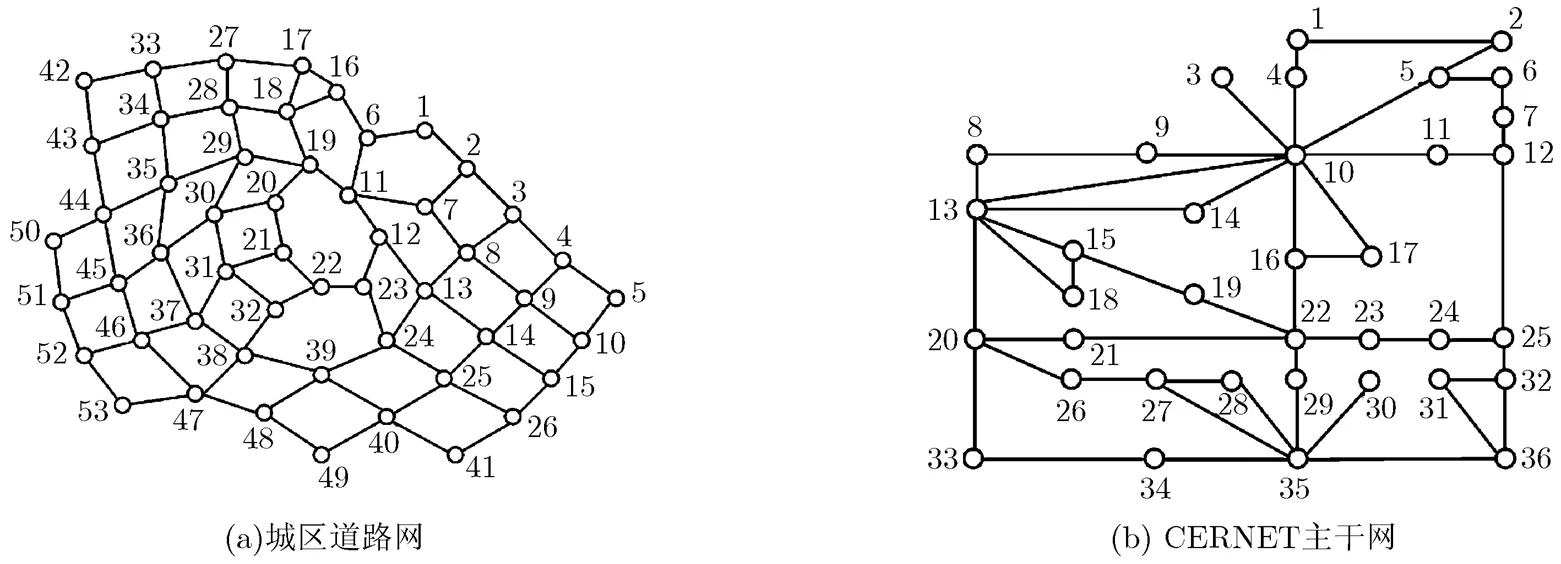
图3 真实网络拓扑

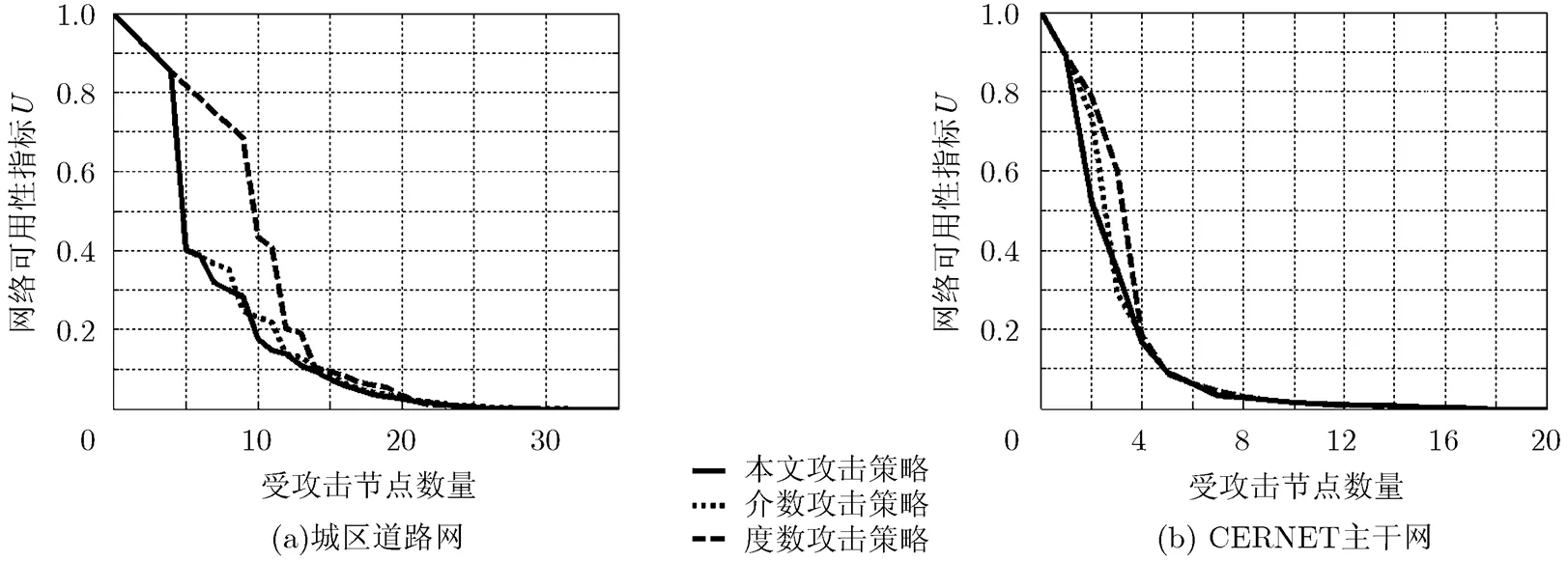
图4 真实网络上的攻击效果

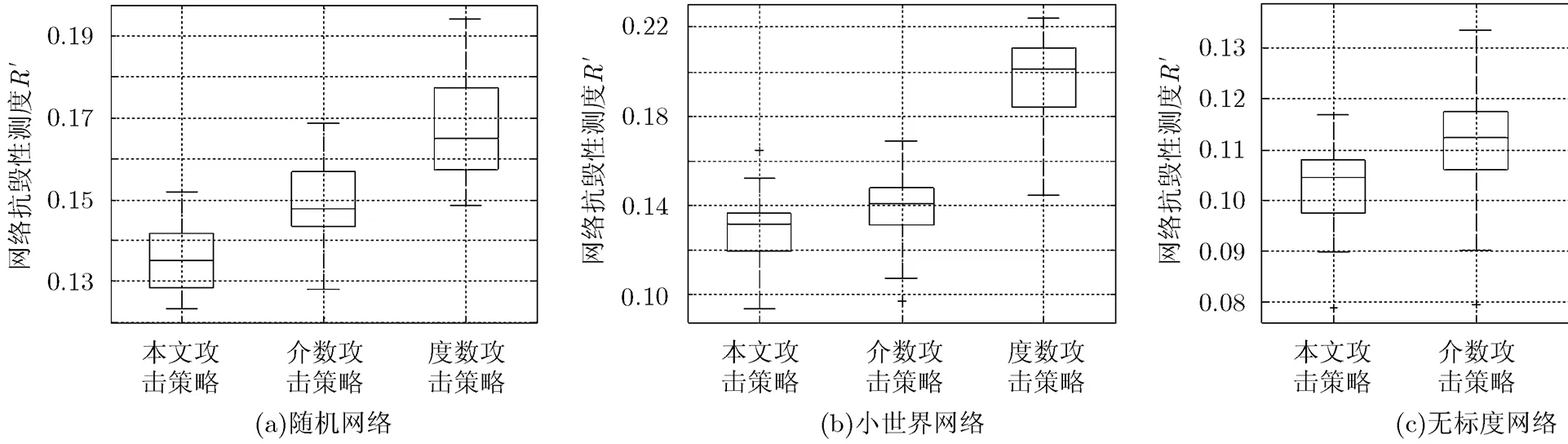
图5 模拟网络上的攻击效果

仿真实验3 复杂网络节点重要度排序与复杂网络节点攻击策略之间具有密切联系，当将节点重要度排序结果视为一个节点攻击序列时，这种重要度排序方法就转化成了一种攻击策略，当将攻击策略构造出的节点攻击序列视为一种重要度排序结果时，这种攻击策略就转化成了一种节点重要度排序方法。因此本文选取几种典型的复杂网络节点重要度排序方法作为节点攻击策略来与本文攻击策略进行对比。考虑到APAR网[20]是节点重要度排序中常用的实验对象，故本文选择APAR网实施攻击，实验结果如图6所示。

在图6所示的4种攻击策略中，本文攻击策略能更快地使ARPA网的可用性降低，该网络在本文攻击策略、文献[17]、文献[18]和文献[19]下的抗毁性测度分别为0.0857, 0.0980, 0.1095和0.1721，即本文所提策略的攻击效果比其它策略分别优12.55%, 21.74%和50.20%。实验结果表明本文所提策略同样优于基于节点重要度排序思想导出的攻击策略，换而言之，本文策略也能较好地应用于节点重要度排序工作中。

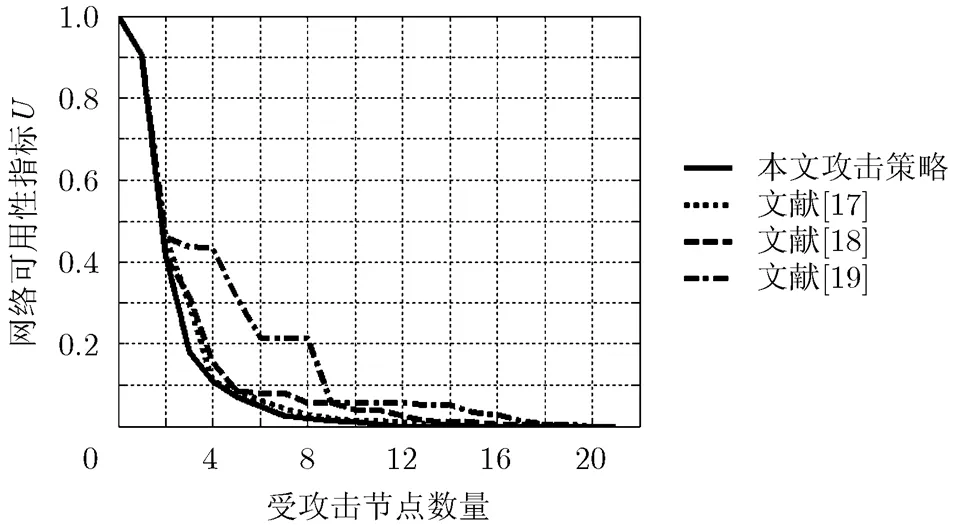
图6 ARPA网上的攻击效果

5 结束语

研究更为有效的复杂网络攻击策略是促进复杂网络防护措施发展完善的重要途径。本文分析了传统攻击策略存在的不足并引入优化思想设计了一种新策略，主要有以下几点工作：(1)基于网络可用性指标提出了节点攻击序列攻击效果的测度方式；(2)以最大化攻击效果为目标建立了节点攻击序列构造的优化模型；(3)基于禁忌搜索设计了模型的求解算法。不同类型网络上的实验结果证明了本文所提攻击策略的有效性和优越性。本文下一步工作是在此基础上研究网络结构的抗毁性设计问题。

[1] JIANG Y and WANG Y B. Analysis of attack and defense strategies on complex networks[C]. Proceedings of International Conference on Sensor Network Security Technology and Privacy Communication System, Harbin, China, 2013: 58-62.

[2] ALBERT R, JEONG H, and BARABASI A L. Error and attack tolerance of complex networks[J]., 2000, 406: 378-382. doi: 10.1038/35019019.

[3] HOLME P, KIM B J, YOON C N,. Attack vulnerability of complex networks[J]., 2002, 65(5): 056109. doi: 10.1103/PhysRevE.65.056109.

[4] BELLINGERI M, CASSI D, and VINCENZI S. Efficiency of attack strategies on complex model and real-world networks [J]., 2014, 414: 174-180. doi: 10.1016/j.physa.2014. 06.079.

[5] NIE T Y, GUO Z, ZHAO K,. New attack strategies for complex networks[J]., 2015, 424: 248-253. doi: 10.1016/j.physa.2015.01.004.

[6] 聂廷远, 郭征, 李坤龙. 复杂网络的攻击策略研究[J]. 计算机仿真, 2015, 32(7): 286-289. doi: 10.3969/j.issn.1006-9348. 2015.07.063.

NIE Tingyuan, GUO Zheng, and LI Kunlong. A study of attack strategies for complex networks[J]., 2015, 32(7): 286-289. doi: 10.3969/j.issn.1006- 9348.2015.07.063.

[7] XIAO S and XIAO G. On intentional attacks and protections in complex communication networks[C]. Proceedings of IEEE Global Telecommunications Conference, San Francisco, CA, USA, 2006: 1-5.

[8] 李涛, 裴文江. 针对重叠社团结构的复杂网络多靶向攻击策略[J]. 北京邮电大学学报, 2010, 33(3): 34-39. doi: 10.3969/ j.issn.1007-5321.2010.03.007.

LI Tao and PEI Wenjiang. Multi-targets attack strategy based on the overlapping community structure of complex networks[J]., 2010, 33(3): 34-39. doi: 10.3969/j.issn. 1007-5321.2010.03.007.

[9] WANG H, HUANG J Y, XU X M,. Damage attack on complex networks[J]., 2014, 408: 134-148. doi: 10. 1016/j.physa.2014.04.001.

[10] ANURAG S, RAHUL K, and YATINDRA N S. Impact of structural centrality based attacks in complex networks[J]., 2015, 46(2): 305-324. doi: 10.5506/ APhysPolB.46.305.

[11] DENG Y, WU J, and TAN Y J. Optimal attack strategy of complex networks based on tabu search[J]., 2016, 442: 74-81. doi: 10.1016/j.physa.2015.08.043.

[12] HERRNANN H J, SCHNEIDER C M, MOREIRA A A,. Onion-like network topology enhances robustness against malicious attacks[J].:, 2011, 1: P01027. doi: 10.1088/1742-5468/ 2011/01/P01027.

[13] SCHNEIDER C M, MOREIRA A A, ANDRADE J S,. Mitigation of malicious attacks on networks[J].,2011, 108(10): 3838-3841. doi: 10.1073/pnas. 1009440108.

[14] LOUZADA V H P, DAOLIO F, HERRMANN H J,. Smart rewiring for network robustness[J]., 2013, 1(2): 150-159. doi: 10.1093/comnet/xxx000.

[15] BURKE E K and KENDALL G. Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques[M]. New York: Springer, 2005: 165.

[16] LATORA V and MARCHIORI M. Efficient behavior of small-world networks[J]., 2001, 87(19): 198701. doi: 10.1103/PhysRevLett.87.198701.

[17] 陈勇, 胡爱群, 胡啸. 通信网中节点重要性的评价方法[J]．通信学报, 2004, 25(8): 129-135. doi: 10.3321/ j.issn:1000-436X. 2004.08.018.

CHEN Yong, HU Aiqun, and HU Xiao. Evaluation method for node importance in communication networks[J]., 2004, 25(8): 129-135. doi: 10.3321/j.issn: 1000-436X.2004.08.018.

[18] 于会, 刘尊, 李勇军. 基于多属性决策的复杂网络节点重要性综合评价方法[J]. 物理学报, 2013, 62(2): 1-9. doi: 10.7498/ aps.62.020204.

YU Hui, LIU Zun, and LI Yongjun. Key nodes in complex networks identified by multi-attribute decision-making method[J]., 2013, 62(2): 1-9. doi: 10.7498 /aps.62.020204.

[19] 秦李, 杨子龙, 黄曙光. 复杂网络的节点重要性综合评价[J]. 计算机科学, 2015, 42(2): 60-64. doi: 10. 11896/j.issn.1002- 137X.2015.2.013.

QIN Li, YANG Zilong, and HUANG Shuguang. Synthesis evaluation method for node importance in complex networks [J]., 2015, 42(2): 60-64. doi: 10.11896/ j.issn.1002-137X.2015.2.013.

[20] PAGE L and PERRY J. Reliability polynomials and links importance in networks[J]., 1994, 43(1): 51-58. doi: QK.IEL.1994.0000024.0007056. 00285108.

Node Attack Strategy of Complex Networks Based on Optimization Theory

SUN Yu YAO Peiyang ZHANG Jieyong FU Kai

(,,’710077,)

This study proposes a new node attack strategy of complex networks by analyzing the disadvantages of traditional strategies. The idea of the new strategy is to treat the construction problem of node attack sequence as an optimal problem rather than an evaluation problem. To achieve this strategy, the study designs a survivability index of complex networks to measure the attack effect created by a node attack sequence, then establishes a construction model of node attack sequence with the goal to maximize attack effect, and further brings forward an algorithm based on tabu search to solve the model. Experiment results from real networks and simulated networks show that the new strategy is more effective than others.

Complex networks; Attack strategy; Survivability measurement; Optimization model; Tabu search

TP393; N949

A

1009-5896(2017)03-0518-07

10.11999/JEIT160396

2016-04-22；改回日期：2016-10-31；

2016-12-20

孙昱 suny.z@qq.com

国家自然科学基金(61573017)

The National Natural Science Foundation of China (61573017)

孙 昱： 男，1989年生，博士生，研究方向为指挥信息系统.

姚佩阳： 男，1960年生，教授，博士生导师，研究方向为指挥控制理论与技术.

张杰勇： 男，1983年生，讲师，博士，研究方向为指挥控制系统建模与分析.

付 凯： 男，1987年生，博士生，研究方向为复杂系统建模与仿真.