迭代优化最小化唯相位波束形成

吴 凯 苏 涛 李 强



迭代优化最小化唯相位波束形成

吴 凯*苏 涛 李 强

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071) (西安电子科技大学信息感知技术协同创新中心 西安 710071)

为了增强唯相位波束形成(Phase-Only Beamforming, POB)的干扰和噪声抑制性能，提高非凸POB权值求解的实时性，该文设计了迭代优化最小化(Iterative Majorization Minimization, IMM)唯相位最小方差无失真响应波束形成器(Minimum Variance Distortion-less Response Beamformer, MVDRB)。将无失真响应约束转化成最大化期望方向阵列响应，推导了二次型目标函数的上界，得到IMM-POB优化模型，并进一步推导出每次迭代的闭式最优解。仿真分析表明所设计的IMM-POB：在相同输入信噪比下，可获得高于现有迭代算法和最优MVDRB的信干噪比改善；干扰抑制性能几乎完全逼近最优MVDRB，且具有更优的噪声抑制性；受快拍数影响较小；闭式最优权仅包含单次矩阵和向量乘法，使算法具有较强的实时性，可应用于大规模阵列。

大规模阵列；波束形成；唯相位；最小方差无失真响应；优化最小化

1 引言

波束形成技术广泛应用于雷达、通信、声呐和医学等领域，通过调整阵列发射或接收权值，实现波束赋形、低副瓣和自适应干扰抑制等功能。按照是否对各阵元发射/接收信号施加恒模约束，可分为幅相加权和唯相位波束形成(Phase-Only Beamforming, POB)。POB具有较强的工程实用意义：可以充分利用微波组件功率，避免能量损失[4]；由于仅需要调整接收相位，可通过移相器直接实现，降低系统复杂度，提高系统稳定性[5]。另外，由于移相器的广泛应用，已有的天线阵列系统可通过少量改进实现干扰置零等设计，节约已有系统升级成本；且考虑大规模天线阵列校准的难度和复杂度，一次校准之后阵列的幅度加权通常保持不变[6]，此时只能通过POB获得期望波束响应。相比于幅相加权波束形成器设计，POB由于具有恒模约束，是非凸多模问题。国内外已存在大量针对POB的优化设计和求解方法，可以总结为3类：启发式方法[7]、全局优化[4, 8]、局部优化。启发式算法效率低，其解虽落在可行域内，但不能保证收敛到全局或局部最优解。全局优化算法的收敛性同样难以保证，且求解时间长，难以适用于大规模阵列。局部优化方法虽然不能保证收敛到全局最优解(与构造的目标函数有关)，但由于该类方法具有相对稳定的收敛特性，且执行效率高，得到较多的重视和发展。

POB局部优化的一个重要途径是转化成经典线性或者非线性优化问题，并通过数值方式求 解。文献[9]利用拉格朗日乘子法去除恒模约束，通过数值方式求解得到的非线性规划问题，该方法难以同时形成多个零点。文献[10]采用交替迭代优化的思想，在假设其余阵元相位固定的情况下依次优化每个阵元的相位加权。文献[11]提出基于谢昆诺夫单位圆的唯相位零陷算法，将阵列方向图表示成平面上多项式乘积的形式，通过调整多项式根的位置形成干扰零陷。文献[10, 11]算法复杂度高，且都需要多次迭代，运算量大，难以实时实现。文献[12]以阵列输出信干噪比(Signal to Interference and Noise Ratio, SINR)为目标函数，通过共轭梯度法和牛顿迭代法来搜索唯相位最优权，需要求解Hesse矩阵及其逆矩阵，且容易陷入局部最优。文献[13]提出基于直接数据域的唯相位最小二乘波束形成算法，并通过共轭梯度法求解相位权重，但存在自适应方向图旁瓣电平较高等不足。

POB设计的另一个重要分支是凸优化和相位扰动：凸优化技术已广泛应用于阵列天线设计中[3]。为了利用凸优化实现非凸POB，文献[3, 6]利用半正定松弛技术来优化唯相位问题，在指定角度范围内可以形成比较宽的凹槽零陷。凸优化方法仅能解决POB设计的松弛或近似问题，难以保证POB的设计性能，且凸优化的求解计算复杂度高，不利于实时处理[18]；文献[14]在小相位扰动的假设下，推导了唯相位干扰置零权值的闭式解。文献[15]将相位权重映射到波束空间中，从而将搜索空间维数从阵元数降到干扰数，通过小相位扰动算法在指定方向形成零陷。文献[16]提出了大相位扰动算法，但会在方向图的对称位置形成干扰零陷。文献[17]利用唯相位加权在方向图指定角度范围内形成宽的零陷，并使用文献[15]中方法在波束空间中使用搜索算法来得到唯相位权重。文献[5]借助小相位扰动，利用一阶泰勒展开近似，将非凸POB转化成迭代二阶锥规划(Iterative Second Order Cone Programming, ISOCP)问题，可利用内点法、序列二次规划等方式求解，是目前性能较好且实时性较强的设计。扰动法将权值的优化设计转化成扰动量的估计，但扰动量难以确定，且POB性能易受扰动量的影响。

为了提高POB的干扰噪声抑制性能和设计实时性，本文主要研究了唯相位最小方差无失真响应波束形成器(Minimum Variance Distortion-less Response Beamformer, MVDRB)设计。首先，将无失真响应约束转化成最大化期望方向阵列响应，并添加在原最小方差目标函数中；然后，借助优化最小化(Majorization Minimization, MM)算法[19, 20]，寻求所得二次型目标函数的上界，构造了以新的上界函数为目标函数，满足恒模约束的迭代POB算法，命名为迭代优化最小化(Iterative MM-POB, IMM-POB)算法，推导了每一次迭代的闭式最优解，形式简单，仅包含单次矩阵和向量乘法，保证了IMM-POB算法的实时性。最后，仿真验证了本文IMM-POB的有效性。

2 问题描述

考虑任意阵列，图1给出了3维直角坐标系下的阵元位置和回波示意图。

假设有个阵元和个互不相关的回波信号(由1个期望信号和-1个干扰信号组成)。则时刻阵元接收基带信号构成的快拍矢量为

(2)

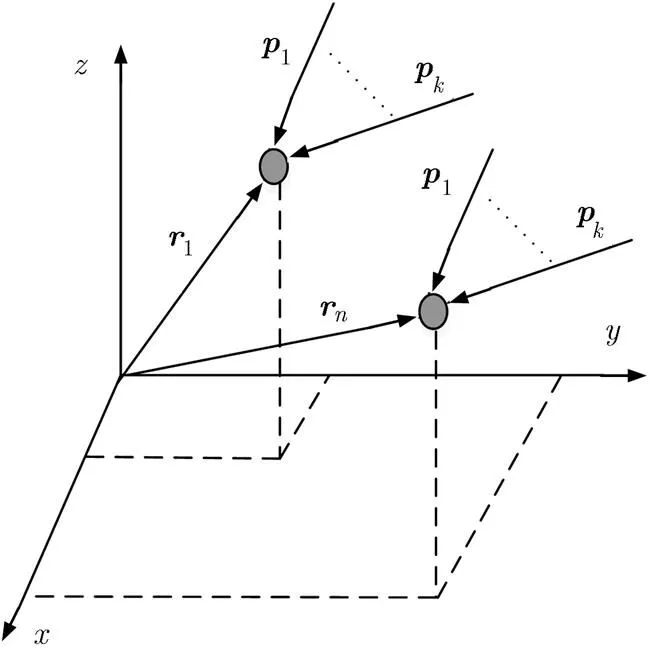
图1 阵列几何模型

传统MVDRB要求阵列保证特定方向无失真的条件下，输出功率最小，因而可以描述为式(3)所示的最优问题：

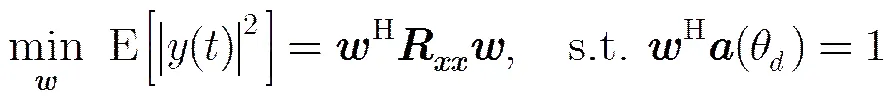
(4)

该问题为非凸多模问题，难以在多项式时间内精确求解。为了与文献[5]对比，首先给出其ISOCP算法模型。利用权值扰动，即在权值的基础上增加相位扰动项，并利用一阶泰勒展开，将式(4)转化成

3 迭代优化最小化(MM)唯相位波束形成器设计

3.1 MM算法

MM算法[19, 20]将复杂目标函数转化成一系列简单迭代优化过程。若原问题为, MM算法将在处寻求目标函数的上界，并得到迭代优化问题，要求原目标函数和优化上界函数之间满足如下关系：

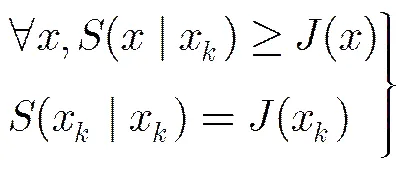
为了采用MM算法构造IMM-POB，首先介绍一种二次型上界函数的构造方式。凸函数曲率有界且二次可微，如果存在矩阵M满足为半正定矩阵，则有[19]

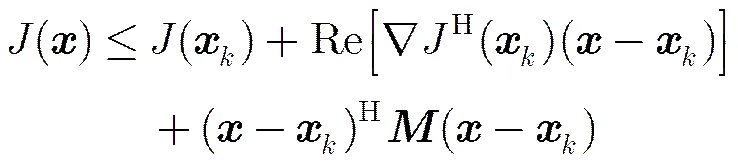
3.2 IMM-POB设计

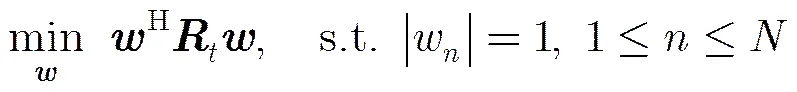
证明 式(4)和式(8)给出的POB设计模型的等价性，可以通过不含模1约束时最优解的等价性得以证明。因而，将首先证明本文给出的式(8)的构造方式与式(9)给出的传统最大信干噪比(Maximum Signal to Interference and Noise Ratio, MSINR)准则下的最优波束形成器的等价性；其次，证明式(9)给出的MSINR最优波束形成器与式(4)给出的MVDR最优波束形成器等价。

(10)

在不考虑模1约束的条件下，式(8)给出的最小问题具有闭式最优解。令其目标函数关于权矢量的导数为0，得，则式(8)的最优解为

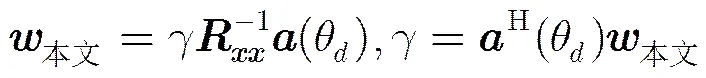
根据式(1)本文建模的回波信号，得到阵列回波自相关矩阵与回波中的信号自相关和干扰噪声自相关矩阵之间的关系为

(12)

则由矩阵求逆引理，

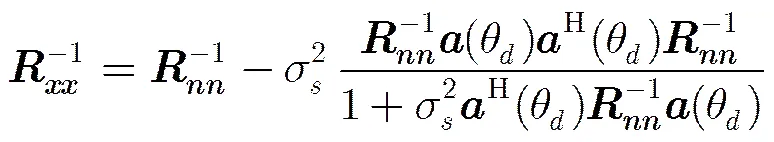
将式(13)代入式(11)有

(14)

对比式(10)和式(14)可以看出，本文构造的最优波束形成器的最优解与MSINR准则下的最优波束形成器的最优解差别仅在解的常复系数和，该差异并不影响最优波束形成器的性能。

在不考虑模1约束的条件下，式(4)传统MVDRB的最优权为

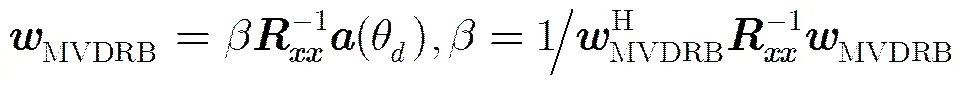
同理，将式(13) 代入式(15)，可得

(16)

从而证明了传统MVDRB和MSINR最优波束形成器之间的等价性。

至此，已证明本文构造的波束形成器和MVDRB都与MSINR准则下的最优波束形成器等价，因而本文构造的波束形成器和传统MVDRB等价，即式(4)和式(8)描述的优化问题等价。 证毕

式(8)将式(4)转化成仅含模1约束的最小化问题，且目标函数具有二次型形式，满足曲率有界且二次可微，利用式(7)容易得到在处的优化上界为(为权矢量空间中的已知点)

(18)

式(18)可进一步转化为

(20)

表示在上次迭代结果的基础上，构造当次迭代的目标上界函数，最小化上界函数得到当次迭代最优解。从式(20)可进一步推导出第次迭代的最优闭式解，将展开可得

(4)终止条件判断，不满足跳转至步骤(3)，否则停止迭代。

终止条件可以为：相邻两次迭代最优权的欧式距离小于预设门限。对最终迭代结果相对期望方向增益进行归一化处理，即，即可获得MVDRB意义下IMM-POB的最优权值。

3.3 对角厄米矩阵的构造

3.2节分析中，在厄米矩阵为对角阵的假设下得到了IMM-POB优化模型。由，得到：对，有。为厄米正定矩阵，存在酉特征分解，即，其中,为单位矩阵，为的特征值构成的对角矩阵。则由得

4 仿真分析

本节通过与文献[4]、文献[5]和传统最优MVDRB的对比，验证本文算法的有效性和优越性。不失一般性，将采用均匀等距线阵对所提算法性能进行仿真分析，阵元间距为半波长。文献[4]是一种POB设计的全局算法，在传统导向矢量加权向量的基础上，基于遗传算法(Genetic Algorithm, GA)寻找最优的权值扰动量，以实现干扰置零。本文仿真中，GA算法的种群个数为200，初始化种群为扰动量之间的均匀分布样本，采用自适应交叉和变异算子，增强算法的全局收敛特性，采用精英策略，保护优质基因，交叉和精英比分别为0.8和0.05。文献[5]的ISOCP算法(由式(5)给出)是目前性能较好且实时性较强的设计，为了便于对比，采用与之相同的回波场景。远场窄带回波中的期望信号、干扰和噪声互不相关。假设期望信号回波方向为，信号功率为0 dB，且信噪比为0 dB。两个干扰信号波达角分别设置为-30°和40°，干噪比均为30 dB。，本文IMM-POB的迭代终止条件定为相邻两次迭代权值的欧式距离小于。文献[5]算法其他参数设置为和分别为1.1和0.9，，当输出功率小于1.05时算法终止。文中，所有仿真结果均为100次Monte Carlo实验的平均或统计结果。

首先，对比传统MVDRB(权值没有模1约束)、文献[4]GA算法、文献[5]ISOCP算法、以及本文IMM-POB在输入SNR递增的情况下，输出SINR随输入SNR的变化关系。仿真过程中，信号和干扰功率始终保持不变，噪声功率从15 dB以5 dB步长减至-15 dB。图2以误差棒图形式给出了各算法在每种输入SNR下，平均输出SINR及方差。对于文献[4]GA算法，由于算法本身的不确定性较强，导致输出SINR的方差较大，因而仅给出了100次独立实验的均值。从图2可以看出本文IMM-POB算法的输出SINR在低输入SNR情况下与传统MVDRB重合，随着输入SNR升高，最终输出SINR略高于传统MVDRB。文献[4]GA算法和文献[5]ISOCP算法的输出SINR随输入SNR增加近似呈线性增长，且为两条相交线，在低输入SNR情况下，后者有较高的SINR输出，而在SNR较高时，前者输出SINR逐渐增加，接近甚至略高于传统MVDRB。

图3进一步给出了4种算法的输出干扰功率和噪声功率随输入SNR的变化。4条实线代表干扰输出功率，对应的点划线代表噪声输出功率。可以看出本文IMM-POB算法和传统MVDRB均具有较强的干扰抑制能力，且各输入SNR情况下，两者的干扰抑制能力基本相当。文献[4]GA算法的干扰和噪声抑制能力随SNR增大均线性增强，当SNR达到15 dB时，干扰剩余与传统MVDRB相同，噪声剩余比传统MVDRB低约2 dB，因此SINR输出略高出2 dB，与图2吻合。在图2和图3的仿真过程中，文献[5]的ISOCP算法终止条件始终为总信号输出功率低于1.05，图2中ISOCP算法的输出SINR随SNR几乎线性增长，图3中ISOCP算法的输出噪声功率随SNR几乎负线性增长，因而在总输出功率固定的情况下，干扰输出功率近似保持不变，与图2变化趋势相符。与文献[5]的ISOCP算法不同的是，本文IMM-POB算法采用相邻迭代之间的权值变化为算法的终止依据，并没有约束算法的输出功率。文献[5]如果要获得相同的输出SINR改善，需要在迭代过程中不断减小终止门限，但会增长优化时间，且在仿真过程中出现了不收敛的现象。

从图3中输出噪声功率的变化可知，文献[5]和本文算法的输出噪声功率曲线几乎重合，而传统MVDRB的输出噪声功率随着SNR的增大剩余增多。输出噪声功率主要取决于形成的波束方向图。图4给出了不同输入SNR得到的±之间的波束方向图，并对两个方位的干扰零陷进行局部放大，可以看出，随着SNR的增加，传统MVDRB的波束方向图主瓣和整体副瓣电平变化较为明显；文献[4]GA算法因为权值扰动，在形成深零陷的同时，波束方向图出现畸变，整体副瓣电平抬高。文献[5]零陷深度几乎不随SNR变化，始终在-55 dB左右；而本文算法得到的零点深度与传统MVDR算法在不同信噪比下几乎完全相同，且随着输入SNR的增加干扰零陷变深。

图5给出了4种算法得到的积分波束响应(仅取了[-10°,30°]主瓣方位区间)随输入SNR的变化。传统MVDRB算法的积分波束响应随SNR的增大而增大，文献[5]与本文IMM-POB算法的积分波束响应几乎都固定在-11 dB，文献[4]GA算法则呈现出不规律的变化，这与GA算法本身的不确定性与基于GA算法的POB设计模型有关，也是GA算法应用于POB设计的局限。当输入SNR达到15 dB时，传统MVDRB积分主瓣电平比文献[5]ISOCP和本文IMM-POB算法要高出8 dB左右，比文献[4]GA算法高出2 dB左右。相应地，图3中的噪声剩余功率同样高出约8 dB和2 dB，这是因为剩余噪声功率主要取决于形成波束的主瓣增益。

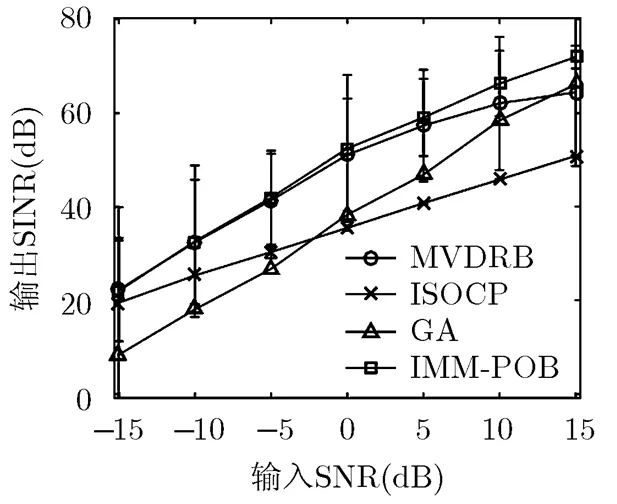
图2 4种算法下输出SINR随输入SNR的变化

图3 4种算法下输出干扰和噪声功率随输入SNR的变化

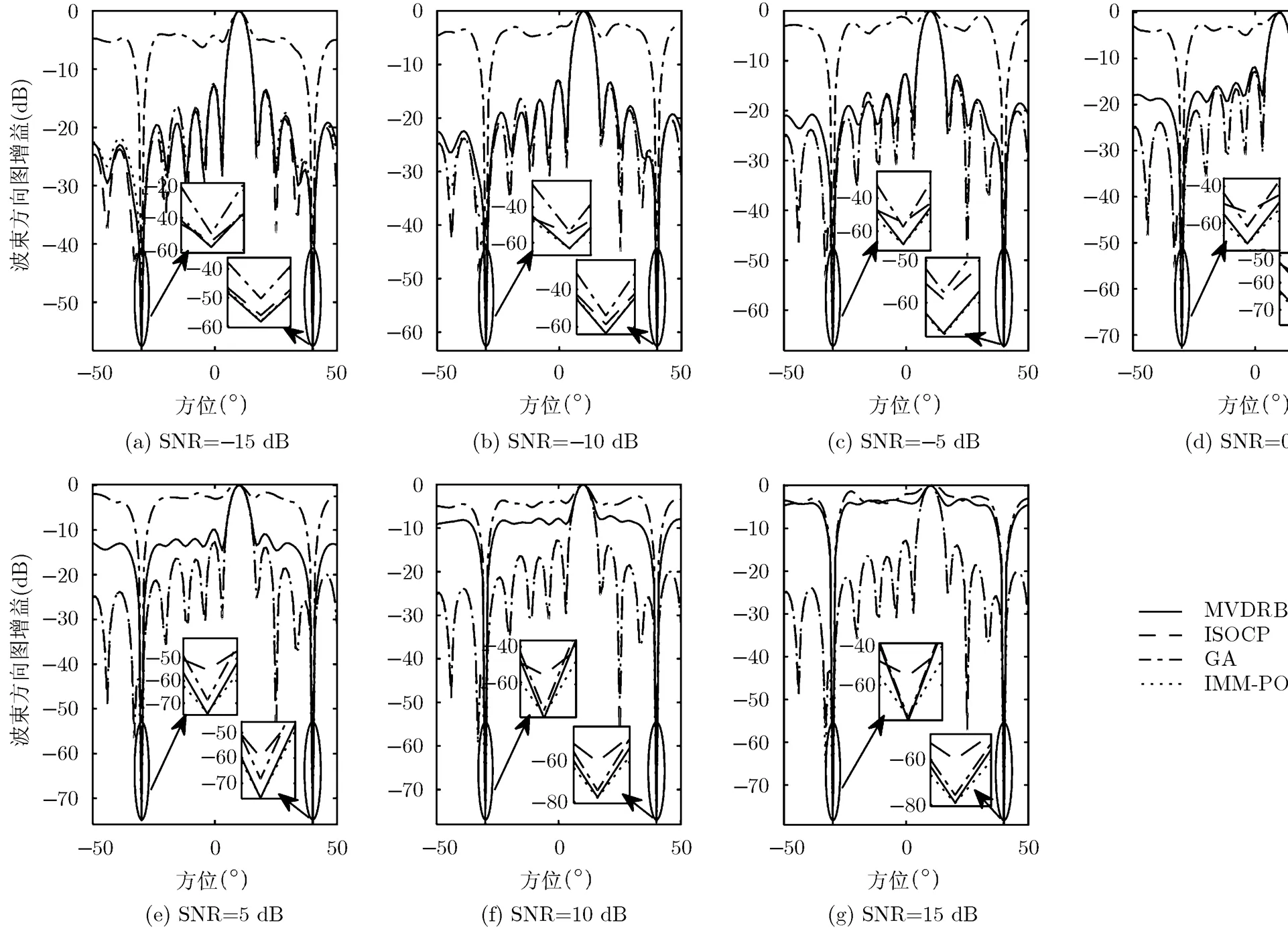
图4 不同输入SNR情况下4种算法形成波束方向图对比

图6对比了输入SNR为10 dB，信号和干扰功率不变的情况下，传统MVDRB算法和本文IMM-POB算法采用不同快拍数估计回波信号的相关矩阵时，输出SINR受影响的程度，仿真中样本数从100以50为步长递增至1000。可以看出本文算法在快拍数较少的情况下仍能获得较高的SINR改善。

表1对比了本文算法与文献[4]GA算法和文献[5]ISOCP算法的运行时间。仿真平台配置为：Intel4核CPU，主频为3.4 GHz，内存16 GB，采用MATLAB 2016a仿真软件。文献[4]GA算法的运行时间较长，且波动较大。由于文献[5]中ISOCP的具体实现方式未知，本文采用MATLAB中的fmincon函数实现ISOCP的求解。对其时间的统计略大于文献[5]给出的运行时间，但是从加速倍数中可以得出与之相近的结论，即文献[5]方法随阵元个数的增加变化较小(因为加速倍数逐渐减小)。本文算法由于每一步迭代都存在闭式解，因而求解效率较高。

5 结论

针对唯相位波束形成器的非凸性，本文提出迭代优化最小化唯相位波束形成算法IMM-POB。借助曲率有界且二次可微目标函数的上界，构造了迭代优化最小化设计模型，推导出每次迭代的闭式最优解，形式简单，仅包含单次矩阵和向量乘法，使算法具有较强的实时性且适用于大规模阵列。仿真验证了算法的有效性，相比已有迭代算法和传统最优MVDRB具有更好的信干噪比改善，零点深度逼近最优MVDRB，运行时间远小于已有迭代算法。

表1 运行时间(s)及加速比对比

阵元个数 152025303540455055 文献[4]方法3.86334.87567.145010.094616.353620.473720.524432.711531.7282 文献[5]方法2.36762.23022.4594 2.5206 2.8655 3.2754 3.3791 3.4156 3.4814 本文算法0.23050.25910.3044 0.3450 0.4189 0.4834 0.5819 0.6585 0.7675 加速比(t本文/ t文献[5])10.27168.60758.0795 7.3061 6.8405 6.7758 5.8070 5.1869 4.5360

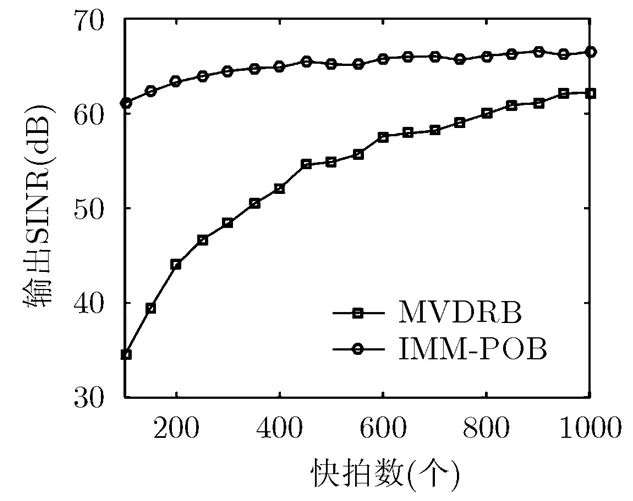
图6 输出SINR随快拍数的变化

[1] WU Kai and SU Tao. Design of generalised sidelobe canceller-based adaptive wideband beamformer without pre-steering delays[J]., 2016, 52(3): 177-179. doi: 10.1049/el.2015.3488.

[2] 吴凯, 苏涛, 靳标, 等. 具有固定反馈权的自适应宽带波束形成器设计[J]. 吉林大学学报(工学版), 2016, 46(1): 303-310. doi: 10.13229/j.cnki.jdxbgxb201601046. WU Kai, SU Tao, JIN Biao,. Design of adaptive broadband beamformer with fixed feedback weights[J].(), 2016, 46(1): 303-310. doi: 10.13229/j.cnki. jdxbgxb201601046.

[3] FUCHS Benjamin. Application of convex relaxation to array synthesis problems[J]., 2013, 62(2): 634-640. doi: 10.1109/TAP. 2013.2290797.

[4] 王学斌, 李会勇, 何子述. 一种基于遗传算法的唯相位宽带零陷波束赋形方法[J]. 中国电子科学研究院学报, 2011, 6(6): 634-638. WANG Xuebin, LI Huiyong, and HE Zishu. Wide null steering based on genetic algorithm by controlling only the current phase[J]., 2011, 6(6): 634-638.

[5] 路成军, 盛卫星, 韩玉兵, 等. 基于迭代二阶锥的唯相位波束形成[J]. 电子与信息学报, 2014, 36(2): 266-270. doi: 10.3724/SP.J.1146.2013.00593. LU Chengjun, SHENG Weixing, HAN Yubing,. Phase-only beamforming based on iterative second-order cone[J].&, 2014, 36 (2): 266-270. doi: 10.3724/SP.J.1146.2013.00593.

[6] KAJENSKI P J. Phase only antenna pattern notching via semidefinite programming relaxation[J]., 2012, 60(5): 2562-2565. doi: 10.1109/TAP.2012.2189709.

[7] SCHOLNIK D P. A parameterized pattern-error objective for large-scale phase-only array pattern design[J]., 2016, 64(1): 89-98. doi: 10.1109/TAP.2015.2500239.

[8] NAYERI P, YANG F, and ELSHERBENI A. Design of single-feed reflect array antennas with asymmetric multiple beams using the particle swarm optimization method[J]., 2013, 61(9): 4598-4605. doi: 10.1109/TAP.2013.2268243.

[9] SHORE R A. The use of nonlinear programming techniques for phase-only[C]. Antennas and Propagation Society International Symposium, Houston, TX, USA, 1983, 21: 23-26. doi: 10.1109/APS. 1983.1149075.

[10] KHZMALYAN A D and KONDRAT’YEV A S. Fast iterative methods for phase-only synthesis of antenna array pattern nulls[J]., 1995, 31(8): 601-602. doi: 10.1049/el:19950432.

[11] MISMAR M J, ISMAIL T H, and ABU-AL-NADI D I. Analytical array polynomial method for linear antenna arrays with phase-only control[J]., 2007, 61(7): 485-492. doi: 10.1016/j.aeue.2006.06.009.

[12] SMITH S T. Optimum phase-only adaptive nulling[J]., 1999, 47(7): 1835-1843. doi: 10.1109/78.771033.

[13] CHOI W S and SARKAR T K. Phase-only adaptive processing based on a direct data domain least squares approach using the conjugate gradient method[J]., 2004, 52(12): 3265-3272. doi: 10.1109/TAP.2004.836410.

[14] STEYAKAL H. Simple method for pattern nulling by phase perturbation[J]., 1983, 31(1): 163-166. doi: 10.1109/TAP.1983. 1142994.

[15] BAIRD C A and RASSWEILER G G. Adaptive sidelobe nulling using digital controlled phase-shifters[J]., 1976, 24(5): 638-649. doi: 10.1109/TAP.1976.1141415.

[16] SHORE R A. Nulling at symmetric pattern location with phase only weight control[J]., 1984, 32(5): 530-533. doi: 10.1109/TAP. 1984.1143360.

[17] GIUSTO R and VINCENT P D. Phase-only optimization for the generation of wide deterministic nulls in the radiation pattern of phased arrays[J]., 1983, 31(5): 814-817. doi: 10.1109/TAP. 1983.1143137.

[18] 吴梦, 刘宏伟, 王旭. 一种循环迭代的MIMO雷达发射方向图设计方法[J]. 电子与信息学报, 2015, 37(2): 322-327. doi: 10.11999/JEIT141043. WU Meng, LIU Hongwei, and WANG Xu. A cyclic iterative method for MIMO radar transmit beampattern design[J].&, 2015, 37(2): 322-327. doi: 10.11999/JEIT141043.

[19] HUNTER D R and LANGE K. A tutorial on MM algorithms [J]., 2004, 58(1): 30-37. doi: 10.1198/0003130042836.

[20] 冯灿, 肖亮, 韦志辉. 压缩感知ISAR成像的全变差优化最小算法[J]. 太赫兹科学与电子信息学报, 2013, 11(5): 775-781. doi: 10.11805/TKYDA201305.0775. FENG Can, XIAO Liang, and WEI Zhihui. ISAR compressive imaging based on majorization-minimization of total variation[J]., 2013, 11(5): 775-781. doi: 10.11805/ TKYDA201305.0775.

Phase-only Beamforming via Iterative Majorization Minimization

WU Kai SU Tao LI Qiang

(,,’710071,)(,,’710071,)

To improve the interference and noise suppression ability of Phase-Only Beamforming (POB) and the real-time performance to obtain the optimal weight of the uon-convex POB, a phase-only Minimum Variance Distortion-less Response Beamformer (MVDRB) via the Iterative Majorization Minimization (IMM) algorithm is designed. The distortion-less response constraint is transformed into maximizing array response in the desired direction. The upper bound function of the objective function in quadratic form is derived which generates the IMM-POB model. The optimal weight in closed-form for each iteration is further deduced. Simulation analysis illustrates that the proposed IMM-POB can obtain better signal to interference and noise ratio improvement compared with the existing iterative POB algorithms and the optimal MVDRB; its interference suppression ability approximates the optimal MVDRB with better noise suppression ability; it is much less sensitive to the number of array taps compared with the optimal MVDRB; it has strong real-time performance and can be applied to large-scale array.

Large-scale array; Beamforming; Phase-only; Minimum variance distortion-less response; Majorization minimization

TN911.7

A

1009-5896(2017)03-0662-08

10.11999/JEIT160472

2016-05-10；改回日期：2016-09-12；

2016-11-14

吴凯 ookaykay@163.com

国家自然科学基金(51405364, 51305323)

The National Natural Science Foundation of China (51405364, 51305323)

吴 凯： 男，1990年生，博士生，研究方向为宽带阵列信号处理.

苏 涛： 男，1968年生，博士生导师，研究方向为实时信号处理及系统设计、自适应信号处理、阵列信号处理、目标检测、ISAR成像等.

李 强： 男，1992年生，博士生，研究方向为实时信号处理设计与实现、雷达系统设计.