Levy噪声驱动下指数型单稳系统的随机共振特性分析

张 刚 宋 莹 张天骐



Levy噪声驱动下指数型单稳系统的随机共振特性分析

张 刚 宋 莹*张天骐

(重庆邮电大学信号与信息处理重庆市重点实验室 重庆 400065)

该文基于绝对值型和指数型势函数，构建了更一般的指数型单稳势函数，深入研究了Levy噪声驱动的指数型单稳系统，并总结出不同特征指数和不同对称参数下，指数型系统参数和Levy噪声强度系数对指数系统共振输出的作用规律。研究表明：在不同Levy噪声驱动下，通过调节参数和均可诱导随机共振(SR)，且当(或)的取值越大时，产生较好随机共振效果(或)的区间越大，从而改善传统SR系统由于参数选择不当造成随机共振效果不佳的问题。此外，通过调节噪声强度系数也能产生随机共振，且较好随机共振区间不随或变化；最后将指数型单稳系统应用于轴承故障检测，效果明显优于传统双稳系统。

指数型单稳系统；Levy噪声；随机共振；轴承故障检测

1 引言

随机振动是指现实世界中无法用确定性函数来描述，但又有一定统计规律的振动。1905年，爱因斯坦[1]在研究水中悬浮的微粒运动问题时发现了随机振动，而后学者们开始广泛而深入地研究随机振动系统。Benzi等人[2]在研究地球的冰川期和暖周期交替出现问题时发现了随机共振(Stochastic Resonance, SR)，在随后的研究中许多经典随机共振系统模型相继被提出，并得到广泛应用。近年来，随机共振发展成为非线性学科中弱信号检测[3,4]最重要的方法之一。

非线性系统中，在特定的噪声强度下，噪声不但不会对激励信号造成负面影响，反而将噪声的一部分能量转移给信号，产生协同效应，这种现象叫随机共振。文献[5]研究了简谐势阱系统，发现系统的输出响应随噪声的某些特征参数呈现非单调变化的现象；文献[6]在经典双稳模型的基础上提出了耦合双稳系统，并将该系统应用于轴承故障检测中。陆思良[7]提出基于Woods-Saxon势阱的随机共振系统，发现其在轴承检测方面优于传统随机共振，且对噪声有较强的鲁棒性；文献[8]研究了白噪声驱动的一阶线性系统广义调参SR现象；文献[9]将简谐势阱推广得到更一般的幂函数型单势阱，且对幂函数型单稳系统的随机共振现象进行深入分析；文 献[10]对三稳系统模型进行规范和定义，分析三稳系统的随机共振特性。

在上述的势阱模型中，传统双稳和单稳势阱模型的研究已较为成熟。单势阱势函数简练，同时也有很好的随机共振性能，因此本文尝试去拓宽随机共振的研究范围，构建更一般的指数型单稳势函数。高斯噪声是一种较理想的噪声，无法有效模拟工程实践的实际噪声，因此引入了非高斯Levy噪声，Levy噪声的波形具有显著的尖峰脉冲特性和拖尾特性，更接近实际工程环境中的随机噪声，且白噪声是Levy噪声在特征指数为2的特殊形式。故而，本文研究了不同和的Levy噪声下，指数型参数以及噪声强度对系统共振输出的作用规律，并且将指数型单稳系统应用于CWRU轴承故障检测。

2 指数型单稳系统模型

在周期信号和Levy噪声共同驱动下，忽略惯性项的过阻尼非线性系统模型为

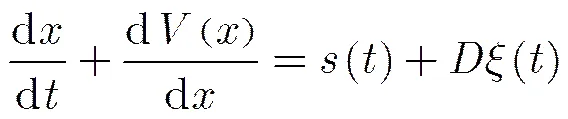
2.1指数型单势阱

目前常用的势函数有很多种，除了传统的单稳和双稳，多项式模型(如FHN模型[4]，三稳态模型)的研究也较多，这些势函数的系统在适当的参数条件下会产生随机共振，但产生随机共振的参数区间不大，参数选择有较大限制。此外，在传统的指数型系统和绝对值型系统中，其势函数形式相对复杂，对于是否能够通过噪声诱导和系统参数诱导实现随机共振，研究较为繁琐。针对以上不足，本文结合指数势和绝对值势的特点，提出了更具一般性的指数型单稳随机共振系统，势函数如式(2)所示，可见式(2)能通过泰勒公式展开成多项式组合，具有普遍性。

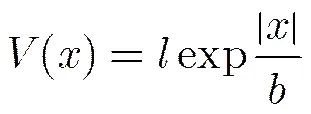
(4)

2.2 Levy噪声的特征函数与产生方法

Levy噪声保持了自然噪声的产生机理和传播机制，其非高斯分布的特点与工程实践中观测到的数据能很好地吻合。假设服从Levy分布，其特征函数表达式为

式中，为特征指数，Levy分布的脉冲特性随的减小而增强，拖尾特性随的减小而减弱。Levy噪声在时服从柯西分布，时服从高斯分布；为对称参数，时噪声呈现对称分布，时分布偏左，时分布偏右；为尺度系数，表示分布样本点偏离均值的离散程度；为位置参数，表示分布的中心位置。

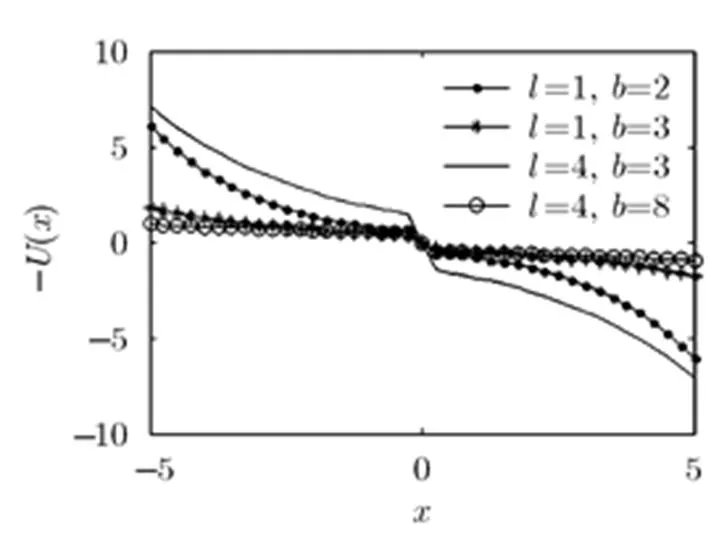
图2 指数型单稳系统势阱力

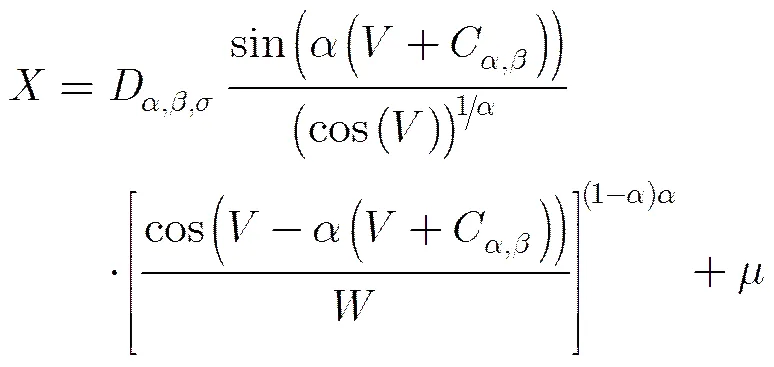
(7)

(9)

2.3数值仿真算法

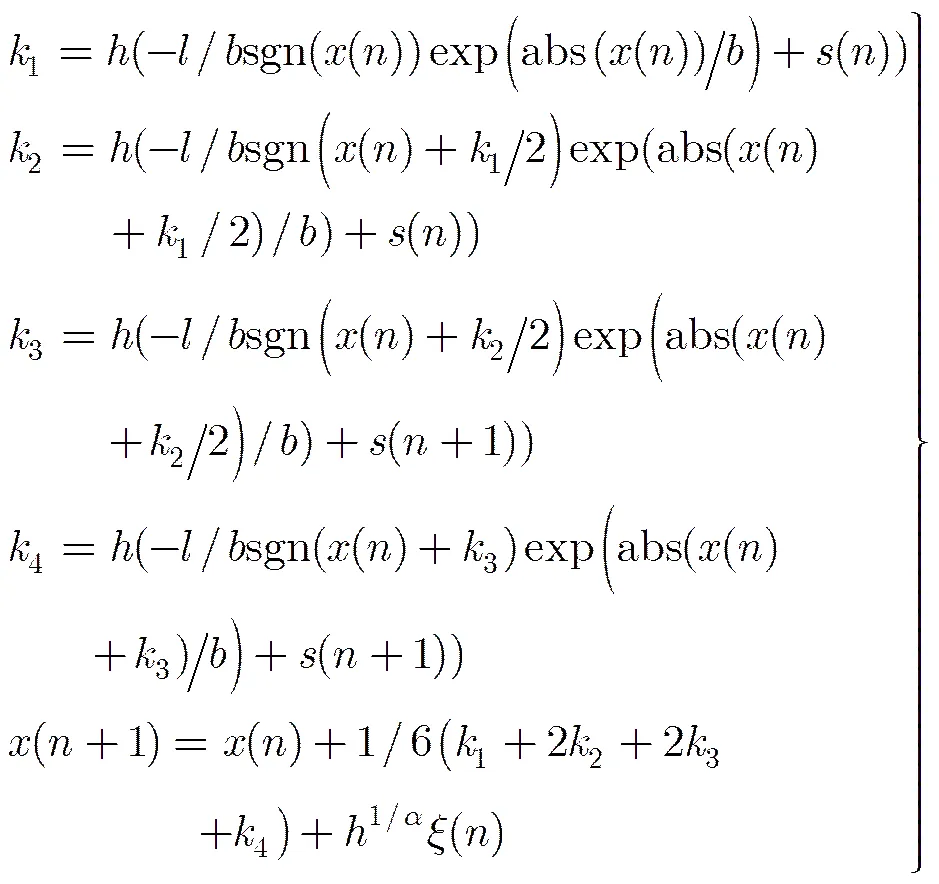
2.4系统性能指标

在众多衡量SR系统性能的指标中输出信噪比的应用最为广泛，本文采用更能反映SR系统对输入信噪比改善作用的信噪比增益[14]作为衡量指标，且有如式(11)定义：

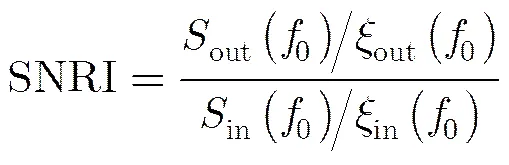
(12)

3 Levy噪声驱动下的指数型单稳系统中随机共振现象

常用的自适应算法有多种，粒子群算法，蚁群算法，人工鱼群算法，遗传算法等智能算法和遍历法等。智能算法适用于多参数寻优，能够快速找到最佳值，其时间复杂度在数据量很大时优于遍历法，但在实际应用中还存在诸如容易产生早熟收敛、收敛速度慢、全局寻优能力差等问题；遍历法选取尽量多的参数对进行仿真，虽然其时间复杂度高于智能算法，但它更倾向于深入观察性能指标的在各个参数对下的变化规律，可以验证智能算法是否正确。为探索指数型单稳系统参数和对SR系统性能的内在规律，本文利用平均信噪比增益为衡量指标的遍历法进行寻优，具体步骤如下：

(2)将含噪的输入信号送入指数型单稳随机共振系统，初始化最佳信噪比增益,,；

下面将深入研究不同Levy噪声环境下，即Levy噪声的特征指数，对称参数取值不同时，系统参数,及噪声强度系数对指数型单稳SR系统输出效应的作用规律。

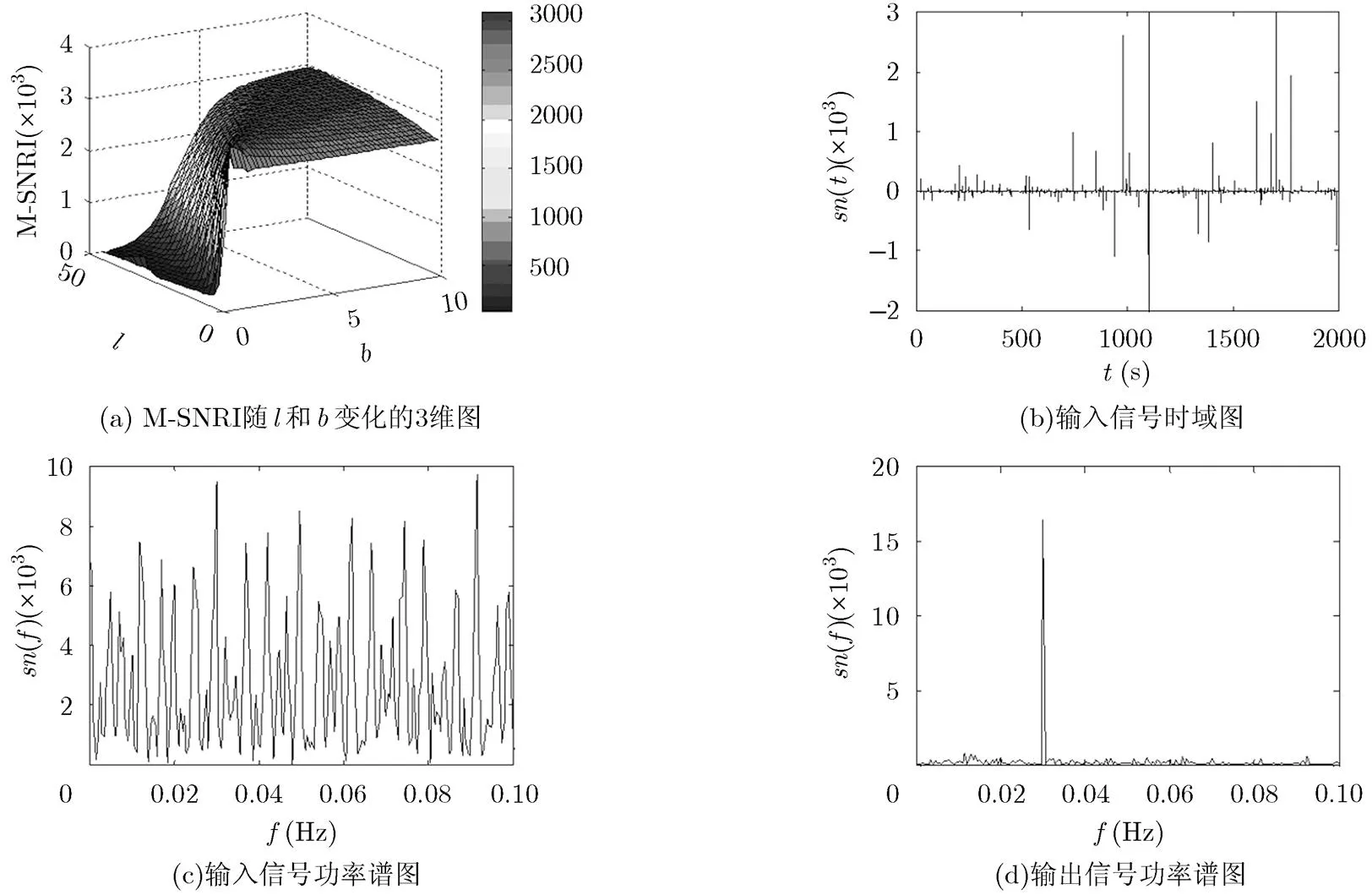
图3自适应随机共振仿真结果图

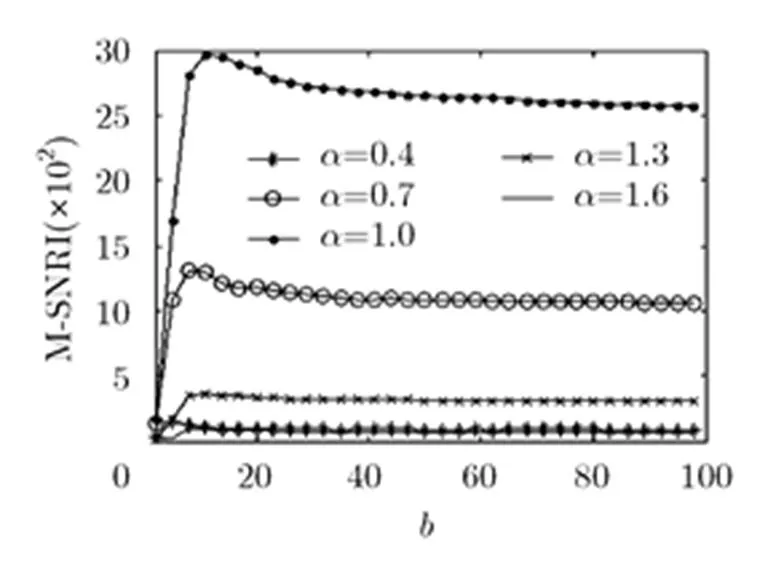
图5 不同取值时随演变曲线

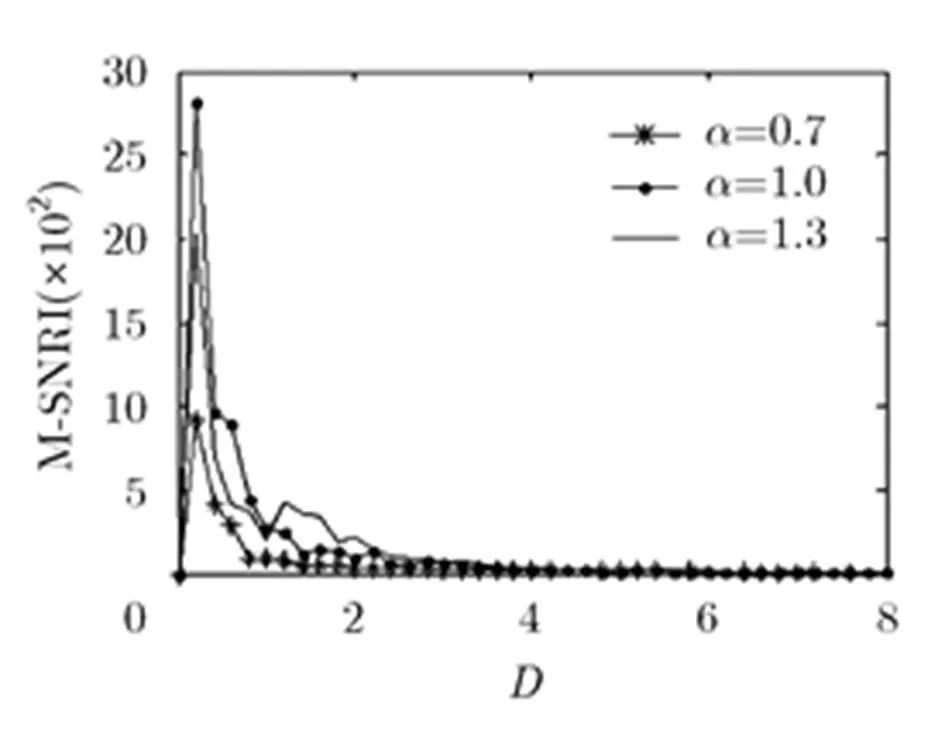
图6 不同取值时随演变曲线

由图4(a)可知，Levy噪声环境下的指数型单稳SR系统的随参数呈先增后减的变化趋势，且在时达到最大值，此时随机共振效果最佳；在时，非线性系统、噪声及输入信号三者达到了最佳匹配关系，即最佳随机共振；当时，随着进一步增大，系统响应时间过长，使得非线性系统、噪声及输入信号三者间的最佳匹配关系逐渐消失，从而导致逐渐下降；由图4(b)和图4(c)可知：当特征指数时，越小，越小；当时，越大，越小；结合图4(a)，图4(b)，图4(c)可以发现，系统随机共振效应较好的区间不随的变化而变化，且在时，系统的最大。

综上可知，Levy噪声驱动的指数型单稳SR系统中，在Levy噪声分布不对称(即)时，对于一个确定的参数(或)，系统的随机共振区间会发生向右(或向左)的偏移。

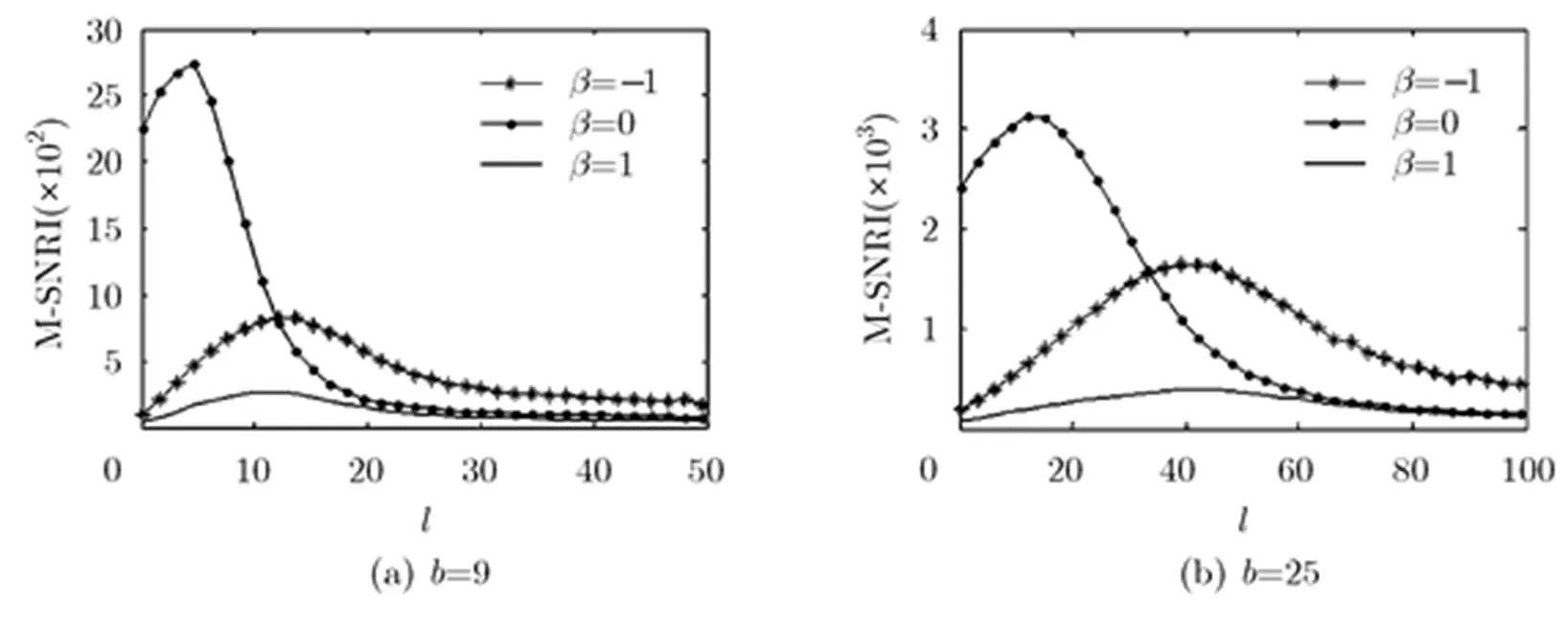
图7 不同取值时随的演变曲线

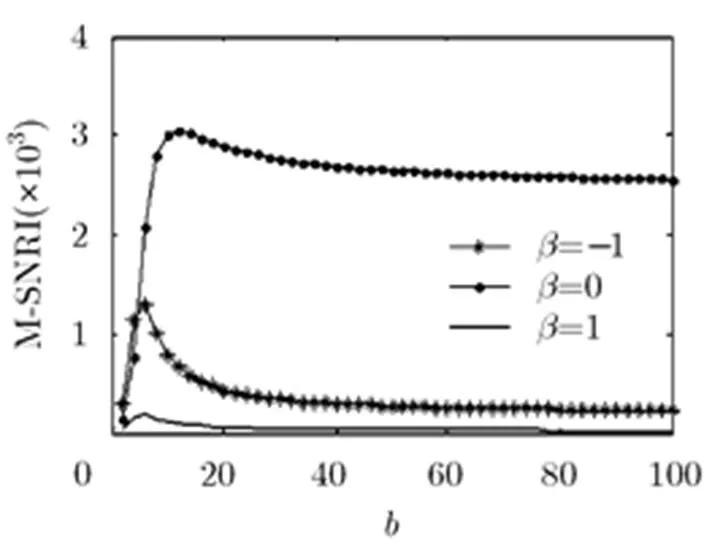
图8 不同取值时随的演变曲线

4 CWRU实验验证

为验证所提的指数型单稳随机共振系统在轴承检测故障中的有效性，本文分别对内圈和外圈的深沟球轴承数据进行了分析实验，也采用双稳系统分析数据。轴承故障数据来自Case Western Reserve University(CWRU)[15]的电气工程实验室，深沟球轴承型号为6205-2RS JEM SKF。转速，采样频率，轴承的尺寸参数见表1。在物理学中，当轴承出现缺陷时，会产生振动信号的周期性脉冲，因此可以通过对脉冲周期来判断故障类型。

表1 6205-2RS JEM SKF轴承参数(mm)

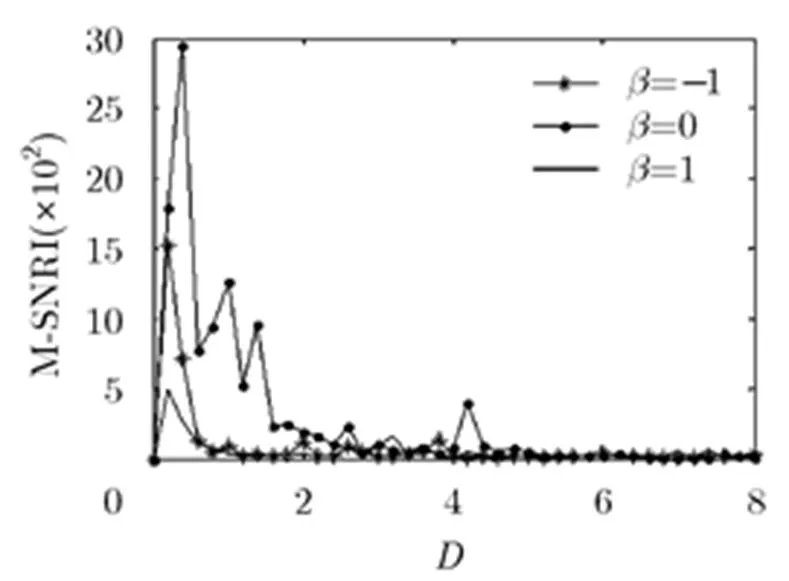
图9 不同取值时随演变曲线

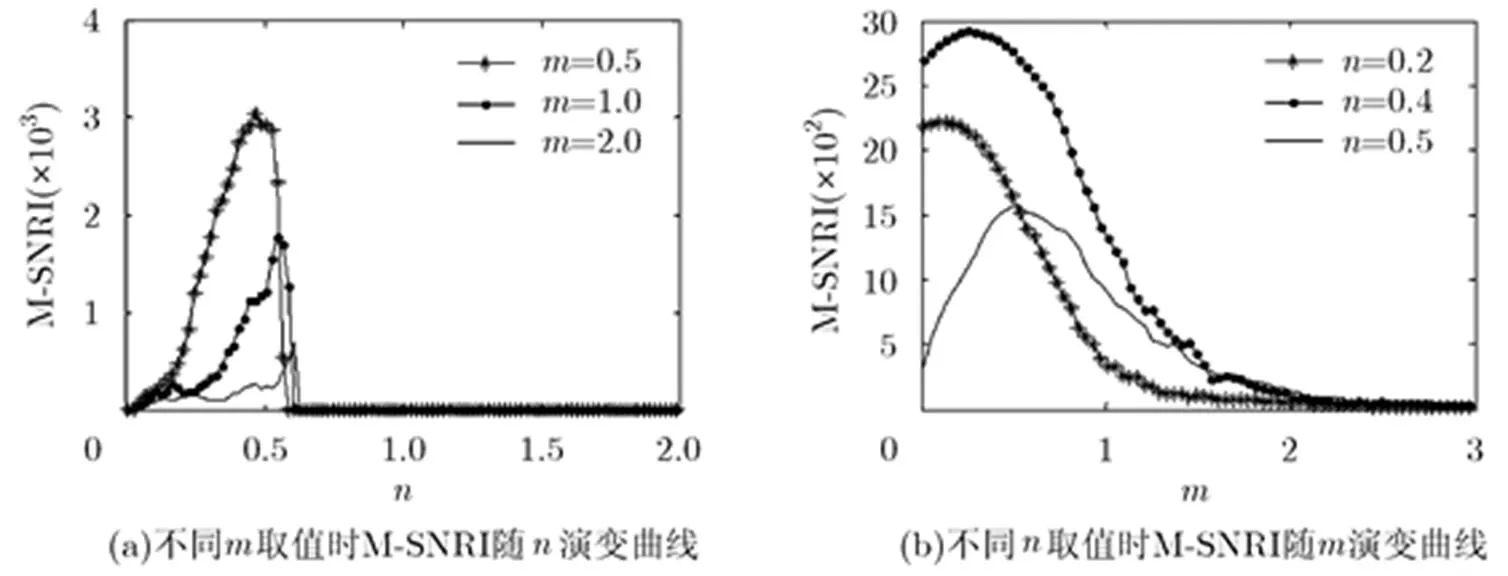
图10 双稳态参数对的影响

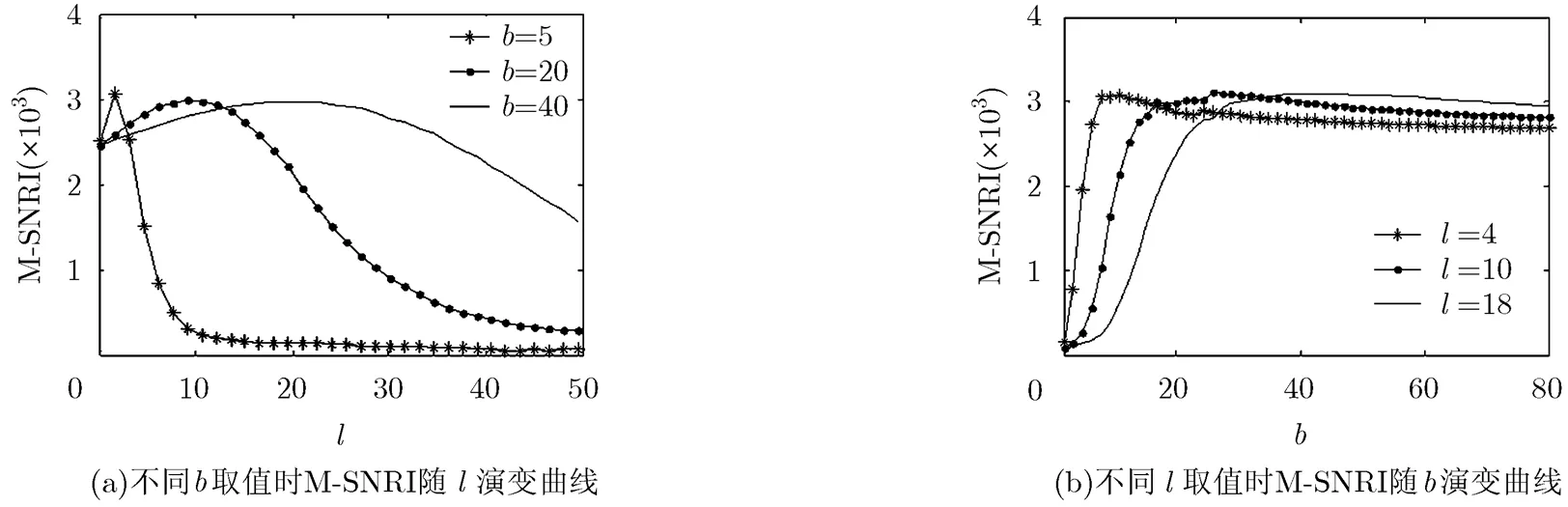
图11 指数势参数对的影响

根据表1中的尺寸参数和转速可以计算出轴承内圈和外圈的故障特征频率，由式(13)[16]可得该轴承外圈的故障频率，内圈的故障频率为,为轴承的转频，。

4.1外圈故障实例

图12(a)为轴承外圈故障信号的时域波形()与频谱()，缺陷信息不能被识别，且的高频段存在很多尖峰干扰。将大频率外圈包络信号通过二次采样，二次采样频率，然后经过上述,的传统双稳SR系统后的输出信号及频谱如图12(b)所示。由图可知，频谱在(在可接受的误差范围内)处出现了尖峰，但在其周围还存在一些干扰频率；将包络信号送入,指数型单稳SR系统后的输出信号及频谱如图12(c)所示，可见相比传统的双稳SR系统，特征频率周围的干扰频率消除了很多，且高频段的尖峰也几乎消失，证明是外圈存在故障，验证了所提方法在弱信号检测中的有效性，且优于传统的双稳SR系统。

4.2内圈故障实例

图13(a)为轴承内圈故障信号的时域波形与频谱，从其时域和频谱看，几乎不能识别特征频率。同样将大频率内圈包络信号经过二次采样后输入,的传统双稳SR系统，输出信号及频谱如图13(b)所示，由图可知，频谱在(在可接受的误差范围内)处出现了尖峰；将内圈包络送入,指数型单稳SR系统后的输出信号及频谱如图13(c)所示，可见特征频率处的峰值相比传统SR系统增强了很多，很容易确定是内圈存在故障，再一次证明了指数型单稳SR系统在故障检测领域的有效性与可靠性。

5 结束语

本文提出了具有一般性的指数型单稳随机共振系统，研究了在Levy噪声驱动下该系统的SR现象。在Levy噪声分布参数,取值不同时，分别探究了指数型单势阱参数和，以及噪声强度系数对的作用规律，得到以下结论：(1) 在不同的Levy噪声下，通过指数型参数诱导或噪声诱导均可实现随机共振；(2)对于指数型单势阱参数(或)诱导随机共振的区间不随变化，随会发生向右(或向左)的偏移，对于噪声诱导随机共振的区间不随或变化；(3)不同时，时系统的共振效应最好；(4)不同时，当Levy噪声分布对称()时，系统的共振效应最好；(5)当噪声分布服从柯西分布()时，存在多组最优参数对使系统达到最佳随机共振，且(或)越大，对应的最佳(或)越大，产生较好随机共振的(或)的区间越大，改善了传统SR系统由于参数选择不当造成随机共振效果不佳的问题。这些结论为指数型单稳系统的参数选择提供了可靠的理论基础，有助于随机共振应用在工程实践中。

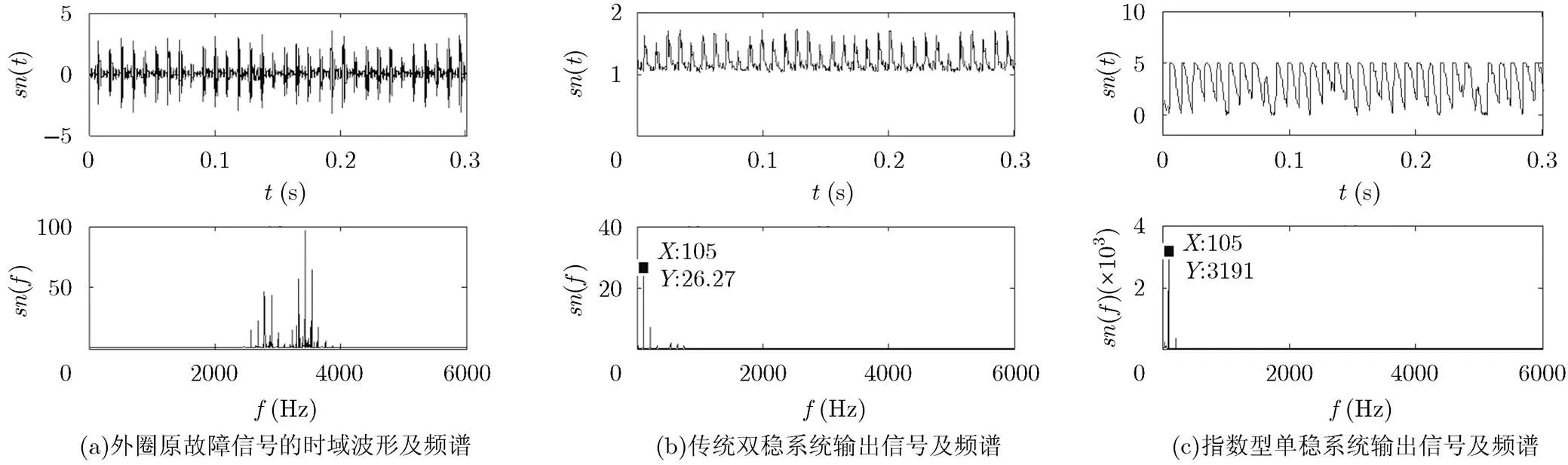
图12外圈故障检测实例

图13内圈故障检测实例

[1] EINSTEIN A.Über die von der molekularkinetischen theorie der wärme geforderte bewegung von in ruhenden flüssigkeiten suspendierten teilchen[J]., 1905,17(8): 549-560.

[2] BENZI R, SUTERA A, and VULPIANI A. The mechanism of stochastic resonance[J].1981, 14(11) 453-457. doi: 10.1088/0305-4470/14/11/006.

[3] 梁军利, 杨树元, 唐志峰. 基于随机共振的微弱信号检测[J].电子与信息学报, 2006, 28(6): 1068-1072.

LIANG Junli, YANG Shuyuan, and TANG Zhifeng. Weak signal detection based on stochastic resonance[J].&, 2006, 28(6): 1068-1072.

[4] WANG Zhanqing, XU Y, and YANG H. Levy noise induced stochastic resonance in an FHN model[J]., 2016, 59(3): 371-375.doi: 10.1007/ s11431-015-6001-2.

[5] GITTERMAN M. Classical harmonic oscillator with multiplicative noise[J].&, 2005, 352(s 2/4): 309-334. doi: 10.1016/j.physa. 2005.01.008.

[6] 郑俊, 林敏. 基于双共振的微弱信号检测方法与试验研究[J]. 机械工程学报, 2014, 50(12): 11-16.doi: 10.3901/JME.2014. 12.011.

ZHENG Jun and LIN Min.Experimental research of weak signal detection method based on the dual-resonance[J].2014, 50(12): 11-16. doi: 10.3901/JME.2014.12.011.

[7] 陆思良. 基于随机共振的微弱信号检测模型及应用研究[D]. [博士论文], 中国科学技术大学, 2015.

LU Siliang. Models and applications of stochastic resonance based weak signal detection[D]. [Ph.D. dissertation], University of Science and Technology of China, 2015.

[8] 田祥友, 冷永刚, 范胜波. 一阶线性系统的调参随机共振研究[J]. 物理学报, 2013, 62(2): 95-102.doi: 10.7498/aps.62.020505.

TIAN Xiangyou, LENG Yonggang, and FAN Shengbo. Parameter-adjusted stochastic resonance of first-order linear system[J]., 2013 62(2): 95-102.doi: 10.7498/aps.62.020505.

[9] 袁季冬, 张路, 罗懋康. 幂函数型单势阱随机振动系统的广义随机共振[J]. 物理学报, 2014, 63(16): 242-252.doi: 10.7498/ aps.63.164302.

YUAN Jidong, ZHANG Lu, and LUO Maokang. Generalized stochastic resonance of power function type single-well system[J]., 2014, 63(16): 242-252.doi: 10.7498/aps.63.164302.

[10] 赖志慧, 冷永刚. 三稳系统的动态响应及随机共振[J]. 物理学报, 2015, 64(20): 77-88.doi: 10.7498/aps.64.200503.

LAI Zhihui and LENG Yonggang. Dynamic response and stochastic resonance of a tri-stable system[J]., 2015, 64(20): 77-88.doi: 10.7498/aps.64.200503.

[11] GILBARG D and TRUDINGER N S. Elliptic Partial Differential Equations of Second Order[M].Berlin Heidelberg, Springer-Verlag1977: 469-484.

[12] CHAMBERS J M. Display and analysis of spatial data: NATO advanced study institute[J]., 1976, 71(355): 768-769.doi: 10.2307 /2285621.

[13] WERON R. On the Chambers-Mallows-Stuck method for simulating skewed stable random variables[J]&, 1996, 28(2): 165-171.doi: 10.1016/0167- 7152(95)00113-1.

[14] 张刚, 胡韬, 张天骐. Levy噪声激励下的幂函数型单稳随机共振特性分析[J]. 物理学报, 2015, 64(22): 72-81. doi: 10.7498/ aps.64.220502.

ZHANG Gang, HU Tao, and ZHANG Tianqi. Characteristic analysis of power function type monostable stochastic resonance with Levy noise[J]., 2015, 64(22): 72-81. doi: 10.7498/aps.64.220502.

[15] ZHANG Haibin, HE Qingbo, and KONG Fanrang. Stochastic resonance in an underdamped system with pinning potential for weak signal detection[J]., 2015, 15(9): 21169-21195.doi: 10.3390/s150921169.

[16] QIAO Zijian and PAN Zhengrong. SVD principle analysis and fault diagnosis for bearings based on the correlation coefficient[J].&, 2015, 26(8): 15-30.doi: 10.1088/0957-0233/26/8/085014.

Characteristic Analysis of Exponential Type Monostable Stochastic Resonance under Levy Noise

ZHANG Gang SONG Ying ZHANG Tianqi

(,,400065,)

Based on the absolute and exponential monostable potential, a generalized exponential type single-well potential function is constructed. The laws for the resonant output of monostable system governed byandof Levy noise are explored under different characteristic indexand symmetry parameterof Levy noise. The results show that the stochastic resonance phenomenon can be induced by adjusting the exponential type parametersandunder anyorof Levy noise.The larger(or) is, the wider parameter interval of(or) can induce SR (Stochastic Resonance). The ESR (Exponential SR) system can solve the problem that the traditional system can not achieve SR due to the improper selection of parameters.The interval ofof Levy noise, which induces good stochastic resonance, does not change withor. At last, the proposed exponential type monostable is applicated to detect bearing fault signals, which achieves better performance compared with the traditional bisabled system.

Exponentialtype monostable system; Levy noise; Stochastic Resonance (SR); Bearing fault detection

TN911.23

A

1009-5896(2017)04-0893-08

10.11999/JEIT160579

2016-06-03；

改回日期：2016-11-25；

2017-01-22

宋莹 740660604@qq.com

国家自然科学基金(61371164)，重庆市杰出青年基金(CSTC2011jjjq40002)，重庆市教育委员会科研项目(KJ130524)

The National Natural Science Foundation of China (61371164), The Chongqing Distinguished Youth Foundation (CSTC2011jjjq40002), The Research Project of Chongqing Educational Commission (KJ130524)

张 刚： 男，1976年生，副教授，研究方向为混沌同步、混沌保密通信、微弱信号检测.

宋 莹： 女，1993年生，硕士生，研究方向为微弱信号检测.

张天骐： 男，1971年生，教授，研究方向为语音信号处理、盲处理、神经网路实现等.