基于二元译码信息的迭代大数逻辑LDPC译码算法及其量化优化

黎相成 陈海强 梁奇 孙友明 万海斌 覃团发



基于二元译码信息的迭代大数逻辑LDPC译码算法及其量化优化

黎相成①②③陈海强②③梁奇②孙友明①③万海斌②③覃团发*①②③

①(华南理工大学电子与信息学院 广州 510640)②(广西大学计算机与电子信息学院 南宁 530004)③(广西多媒体通信与网络技术重点实验室培育基地/广西高校多媒体通信与信息处理重点实验室 南宁 530004)

该文提出一种低复杂度的迭代大数逻辑LDPC译码算法，在迭代过程中所有的译码信息都以二元形式进行传递、处理和迭代更新。所提算法不需要计算外信息，而是利用Tanner图上伴随式的对错状态来评判节点可靠度。与现有的几种迭代大数逻辑译码算法相比，该文算法也不需要信息修正处理，避免了相应的实数乘法操作，具有很低的译码复杂度。此外，该文引入一种特殊的量化处理函数，并给出了基于离散密度进化的参数优化过程。实验仿真表明，该文所提算法与原算法相比，在AWGN信道下可获得约0.3~0.4 dB的性能提升。同时，由于节点间交换传递的译码信息都是基于1个比特位的二元信息，也非常便于硬件的设计与实现。

译码算法；LDPC码；大数逻辑；量化；伴随式信息

1 引言

低密度奇偶校验(Low-Density Parity-Check, LDPC)码是一种逼近香农理论极限的实用好码[1]。从译码信息类型上看，LDPC码的译码算法通常可分为软判决和硬判决译码算法两大类。软判决译码算法性能优异，但计算复杂度高，在迭代过程中必须使用存储器存储大量的缓存数据，不利于工程上实现[2,3]。基于大数逻辑的硬判决译码算法在迭代过程不使用软信息，而是利用校验方程和伴随式等信息进行投票、计数和翻转等操作，从而获得非常低的译码复杂度。例如一步大数逻辑译码算法(OSMLGD)[4]，比特翻转算法(BF)[1]及其加权版本(WBF)等[4]。2009年，Huang等人[5]提出了一种基于可靠度的迭代大数逻辑译码算法(RBI-MLGD)。该算法使用来自信道的接收值作为初始译码可靠度信息，并定义了一种特殊的二进制外信息，迭代过程只涉及整数和逻辑运算，因此具有很低的译码复杂度。然而，RBI-MLGD算法对码的度分布有着严格的要求，并且在性能上与SPA存在一定差距，限制了它在实际中的推广应用[6]。为了提高性能，文献[7]提出了一种改进版的大数逻辑译码算法(MRBI-MLGD)，在变量节点引入修正因子，并用密度进化理论进行了优化。Ngatched等人[8]使用了整数外信息，并基于最小和(Min-sum)原理对RBI-MLGD算法性能进行了提升，但由于它引入了实数乘法，其译码复杂度明显增加。文献[9]基于变量节点更新规则，提出一种改进的BF算法，获得了性能上的提升。文献[10]提出了一种基于列重比例的迭代大数逻辑译码算法(CWB-MLGD)，在变量节点结合量化参数和列重比例等信息进行加权处理，获得了比RBI-MLGD更好的性能，但它仍然是以牺牲译码复杂度作为代价的。Zhang等人[11]提出一种译码过程可只处理部分“活”状态校验节点的译码算法，可降低译码复杂度，但其译码性能没有得到提升，且收敛速度会变慢。

在上述工作基础上，本文提出一种基于二元译码信息的迭代大数逻辑译码算法(BM-MLGD)。与原RBI-MLGD算法相比，本文提出的BM-MLGD算法在迭代过程中只使用伴随式和硬判决结果作为译码信息，校验节点传给变量节点的信息是简单的校验和结果，仍然保持二进制信息特性，便于硬件设计与实现。由于BM-MLGD算法在迭代过程中不需要计算外信息，也不需要任何信息修正操作(避免了现有几种改进算法中的实数乘法操作)，因此具有非常低的译码复杂度。此外，本文引入一种特殊的量化函数，并基于离散密度进化(DE)[12]对量化参数进行了优化。由于量化优化是一次性的离线操作，因此系统不会额外增加复杂度。实验仿真表明，在4~5 bit量化时，本文提出的BM-MLGD译码算法与原RBI-MLGD算法相比，在加性高斯白噪声(AWGN)信道下能获得约0.3~0.4 dB的性能增益，而且其译码复杂度并没有增加。

2 算法描述

2.1 RBI-MLGD及其改进算法

(1)RBI-MLGD算法[5]：校验节点只需计算外信息：

(3)

信息迭代更新规则为

(2)MRBI-MLGD算法[7]：校验节点处理保持不变，变量节点更新规则改为

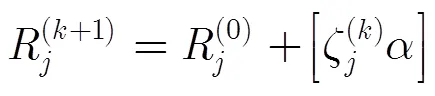
(3)CWB-MLGD算法[10]：校验点只需计算伴随式，引入量化参数以及列重信息，变量节点的更新规则修改为

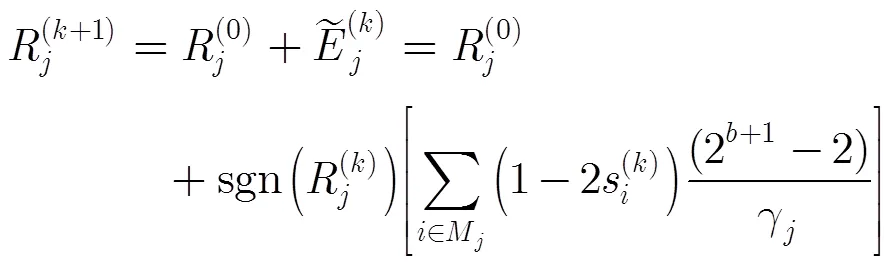
2.2 基于二元译码信息的迭代大数逻辑LDPC译码算法

本文结合Tanner图[13]对算法进行描述。假设第迭代中，与第个变量节点对应的包含的伴随式共有个，不妨设其中校验成功的伴随式个数为，校验失败的伴随式个数为，即。由式(2)可知，如果第个伴随式正确，则与取值相同；否则，与取值相反。于是基于外信息的求和可转变为

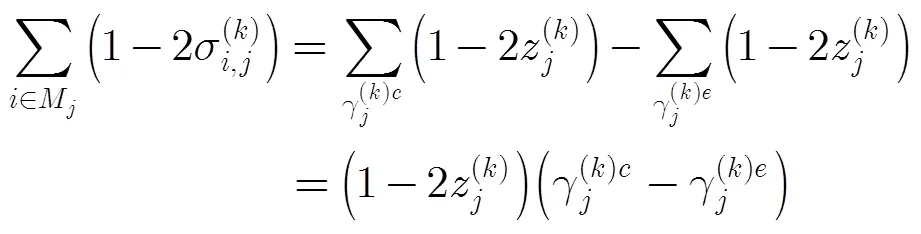
基于伴随式的求和可转变为

(8)

在这种定义下，算法的变量点迭代规则可描述如下：

对RBI-MLGD算法，其迭代规则为

对MRBI-MLGD算法，其迭代规则为

(10)

对CWB-MLGD算法，其迭代规则为

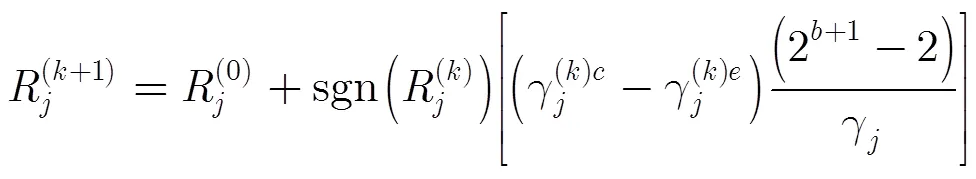
(12)

基于上述迭代规则提出的算法，称为基于二元译码信息的迭代大数逻辑LDPC译码算法(BM- MLGD)，其信息更新有以下特点：(1)与原RBI- MLGD算法不同，本文算法的信息更新总是以信道信息作为基准，可避免可靠度信息在迭代过程中的“溢出”问题；(2)变量节点只需对伴随式信息的正确/错误个数进行简单的统计和投票计算，即可完成对下一次可靠度信息的更新操作。本文算法的主要的步骤如表1所示。

由BM-MLGD算法的信息更新策略可见，本文算法在迭代更新时以信道初始内信息作为基准信息，该信息在迭代过程中保持不变，可避免信息溢出而导致的性能恶化。与原RBI-MLGD算法相比，本文算法在校验节点不需要计算外信息，可节省一些外信息的计算操作。与其它两种改进算法相比，本文算法在变量节点不需要任何参数修正操作，避免了实数乘法，因此能获得更低的译码复杂度。

表1基于二元译码信息的迭代大数逻辑LDPC译码算法(BM-MLGD)

输入：接收值，相关量化参数，最大迭代次数。初始化：将接收信号量化为整数信息可靠度，设置循环迭代次数变量，初始化可靠度信息, 。 译码迭代：当 时，执行以下步骤：步骤1 计算硬判决序列；步骤2 计算，如果，退出迭代；步骤3 对，统计,；步骤4 对，根据式(12 )更新；步骤5 令步进一个单位。输出：迭代过程结束，最终译码输出为。

表2给出了上述几种算法一次迭代所产生的计算复杂度。由表2可见，本文提出的BM-MLGD算法的译码复杂度最低，RBI-MLGD次之；而MRBI-MLGD和CWB-MLGD算法都涉及到实数乘法，具有相对较高的复杂度。

表2 算法迭代一次的复杂度表

算法名称每次迭代的计算量 逻辑操作整数加法实数乘法 MRBI-MLGD CWB-MLGD RBI-MLGD0 BM-MLGD0

3 量化设计与优化量化

本节将引入一种特殊的量化方法，通过优化量化参数来提高本文提出的BM-MLGD译码算法的误码率性能和译码收敛性能。

3.1 量化方案

对于先验等概的二进制离散信源，经AWGN信道传输后，其接收信号的最佳判决门限为0。这意味着在0附近发生错误判决的概率非常大。相应地，对小信号区域做量化处理时，应采取尽可能高的量化解析度。而大信号区域的译码内信息已十分明确，发生错误的概率很小，所以可用相对粗糙的量化解析度进行处理。这种量化方法可达到节省量化比特，减小存储负荷的目的。本文在文献[14]的基础上提出一种接收信号范围可调的量化方案，能够满足上述要求。为进一步减少过载失真，本文把接收信号范围扩大到,表示接收信号的最大允许电平。假设用bit对接收信号幅值进行量化，则量化函数设计为

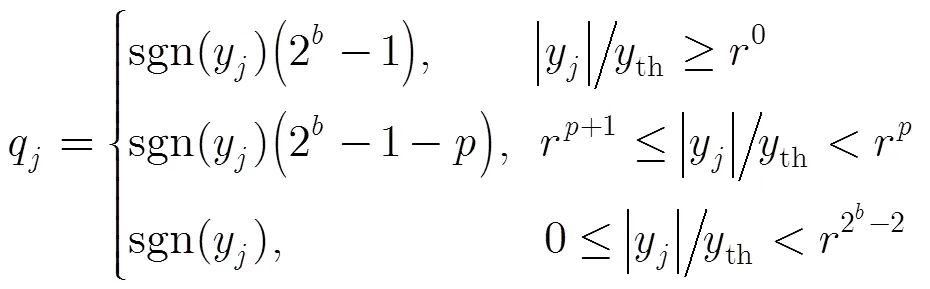
3.2参数优化

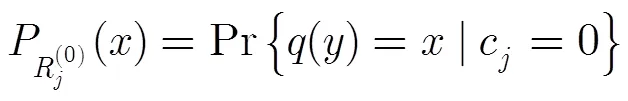
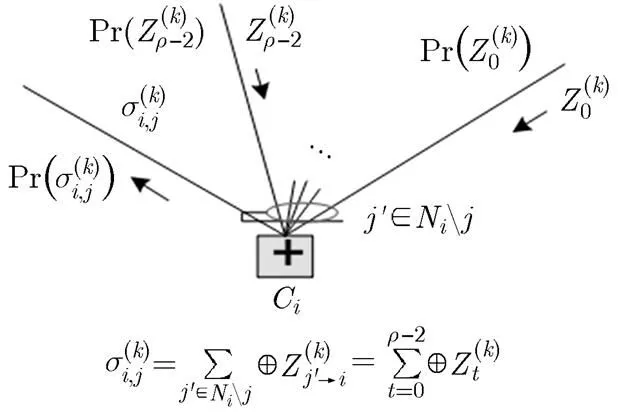
图1 校验节点约束关系

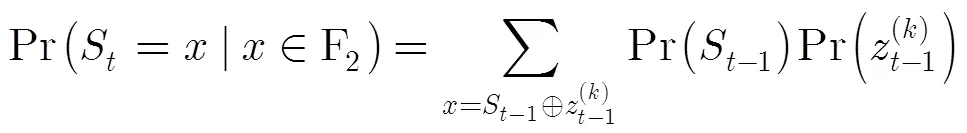
(16)

(2)变量节点迭代：本文算法的变量节点迭代规则如式(12)所示，离散密度进化需要根据其迭代规则，计算新的迭代可靠度信息的概率质量函数pmf。首先，令，计算的pmf，记作。在文献[5]中，伴随式和外信息的关系为。该式表明，当伴随式校验正确时，与取值相同；当伴随式校验错误时，与取值相反。基于此，我们将式(12)变形为

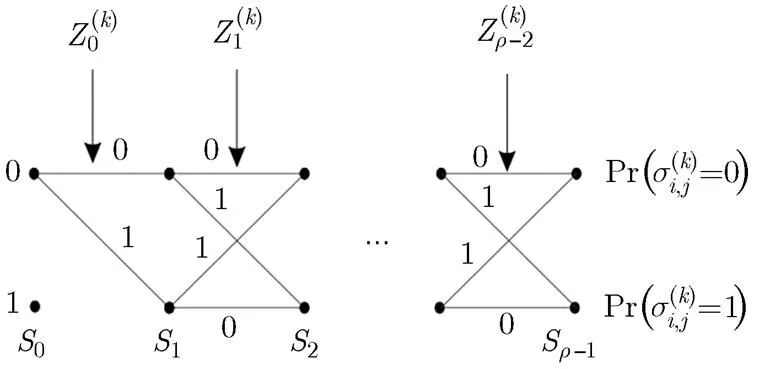
图2 基于Trellis的外信息概率计算

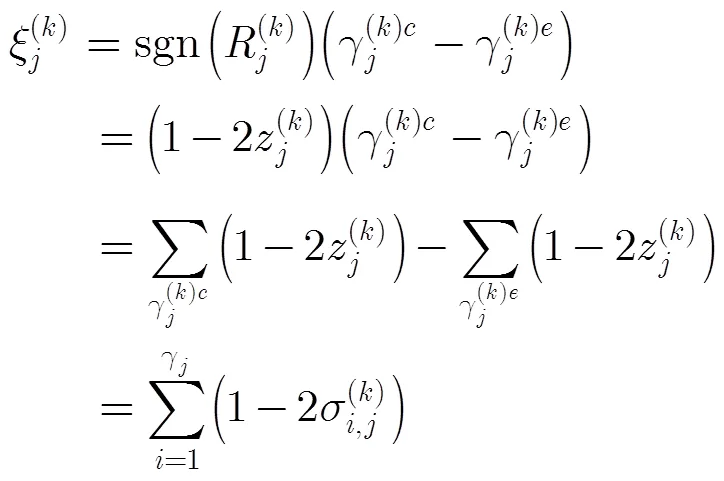
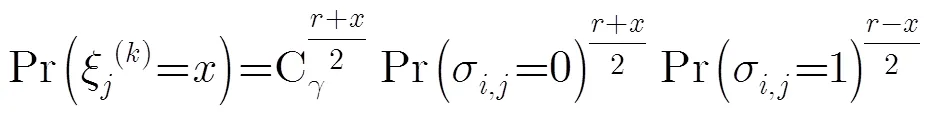
(19)

通过上述的校验节点迭代和变量节点迭代，即可完成一次密度进化迭代的更新过程，得到译码可靠度信息的概率质量函数pmf，从而可计算理论的误码率(BER)。当该BER满足精度要求时(如BER)，即可得到对应的阈值。遍历不同的参数，得到一个的阈值序列；选取阈值序列中的最小值，其对应的解析度参数即为本文所选参数的优化解。

在上述DE过程中，系统的步进和BER等参数都存在一定的精度误差，因此所得到的参数结果只能是次优的。本文将从概率分布特性的角度，给出更直观化的优化结果。假设二元信号调制后的信号星座为，经过AWGN信道后，得到两种概率密度函数，记为以及。在先验等概条件下，这两个概率密度函数的交点(判决门限)正好是原点(=0)。定义概率，其物理意义是接收值落在判决门限和量化电平值之间的概率，计算如式(20)：

(21)

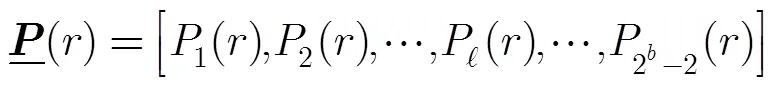
需要指出的是，离散密度进化是对具有无限码长的理想无环结构LDPC码的优化结果。此外，优化过程遍历的操作和确定阈值对应的BER都是在一定精度下进行的。因此，上述DE优化过程得到的参数是一个次优的结果。此外，对于不同的节点度分布，其DE优化结果也是不一样的。

4 实验仿真

实验1 考虑文献[4]基于欧氏几何方法构造的(1023,781)规则循环LDPC码，码率为0.76，行重和列重均为32，属于大数逻辑可译码。仿真参数如下：(1)对RBI-MLGD算法，采用8 bit量化，量化间隔为0.0156; (2)对MRBI -MLGD算法，采用8 bit量化，量化间隔为0.0156，修正系数为3.1；(3)CWB-MLGD算法，采用5 bit量化；(4)对本文BM-MLGD算法，采用5 bit量化，基于DE的解析度参数优化结果为。

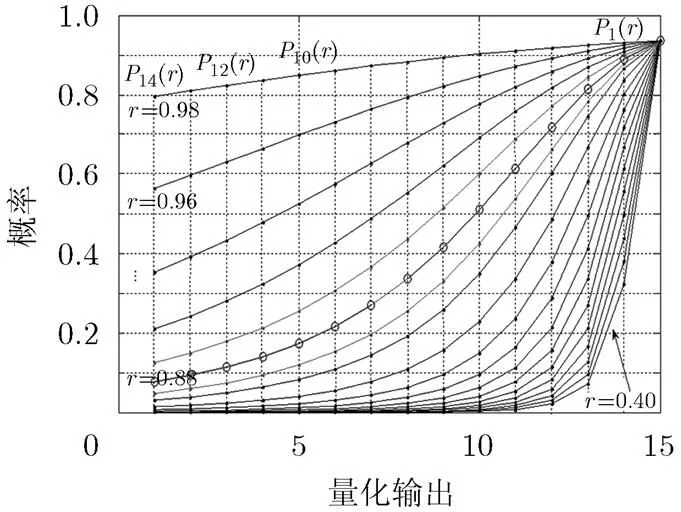
图3 不同量化解析度下概率序列分布图

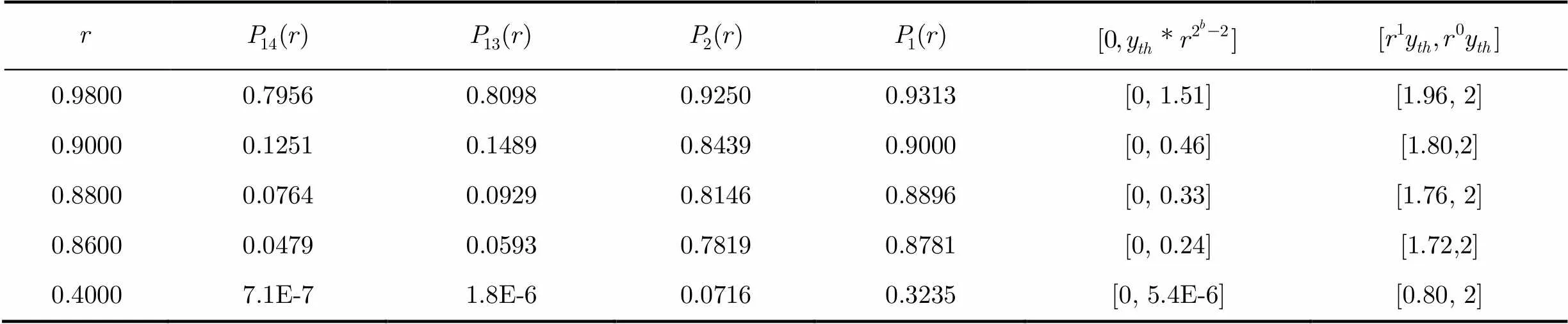
表3 不同量化解析度下的概率序列值

所有译码算法的最大迭代次数设为30次。译码性能结果如图4所示，由图可以看出：

5 bit的BM-MLGD算法的译码性能明显优于8 bit的原RBI-MLGD算法，在BER=时，约获得0.31 dB的译码增益(注意，BM-MLGD的译码复杂度与RBI-MLGD相当)；

5 bit的BM-MLGD算法与经典的SPA译码算法约有0.55 dB的性能差距；

5 bit的BM-MLGD算法与其它两种修正算法，即8 bit的MRBI-MLGD和5 bit的CWB-MLGD算法相比，在性能上几乎没有差别(但BM-MLGD的译码复杂度更低)。

图5给出了BM-MLGD的译码收敛图。由图5可见，本文提出的BM-MLGD在收敛速度上也明显优于原RBI-MLGD算法，并与其它两种修正算法相当。

实验2 类似地，考虑文献[4]中的基于欧氏几何方法构造的(255, 175)规则循环LDPC码，该码的码率为0.69，行重和列重均为16，属于大数逻辑可译码。仿真参数如下：(1)对RBI-MLGD算法，采用8 bit量化，量化间隔为0.0156; (2)对MRBI- MLGD算法，采用8 bit量化，量化间隔为0.0156，修正系数为7.0; (3)对CWB-MLGD算法，采用5 bit量化；(4)对本文BM-MLGD算法，采用4 bit量化，解析度。

所有译码算法的最大迭代次数设为30次。译码性能结果如图6所示，由图可以看出：

4 bit的BM-MLGD算法的译码性能明显优于8 bit的原RBI-MLGD算法，在BER=时，约获得0.41 dB的译码增益；

4 bit的BM-MLGD算法与经典的SPA译码算法约有0.7 dB性能差距；

4 bit的BM-MLGD算法与8 bit的MRBI- MLGD和5 bit的CWB-MLGD性能相当。

图7为BM-MLGD的译码收敛图。由图7可见，BM-MLGD算法的收敛速度明显快于原RBI-MLGD算法。例如，在时，BM-MLGD的平均迭代次数约为2.5次，而RBI-MLGD需要约6.5次。

5 结束语

本文提出了一种使用二元译码信息的迭代大数逻辑LDPC译码算法，只使用伴随式计数结果进行信息处理，不需要计算外信息，也不需要信息修正操作，译码过程只涉及整数和逻辑操作，因此译码复杂度较低。同时，译码算法在节点间交换的译码信息全部为二元比特硬信息，因而也便于硬件实现。此外，本文给出了一种与算法相匹配的量化策略，能够针对不同特性的接收信号定义量化精度。最后，本文基于离散密度进化理论对量化参数进行了优化。仿真实验显示，与原RBI-MLGD算法相比，本文算法能在更低的量化比特下工作，在相当的译码复杂度的前提下，仍获得了约0.3~0.4 dB的性能增益。最后需指出，本文算法属于大数逻辑译码算法，仅适用于列重较大的结构性规则LDPC码；当对非规则的LDPC码进行译码时，性能表现不佳，且会出现错误平层。引入与列重相关的动态修正系数后，可缓解错误平层现象，但会增加算法的复杂度。这些问题可作为本文工作的一个扩展，进行更加深入的研究。

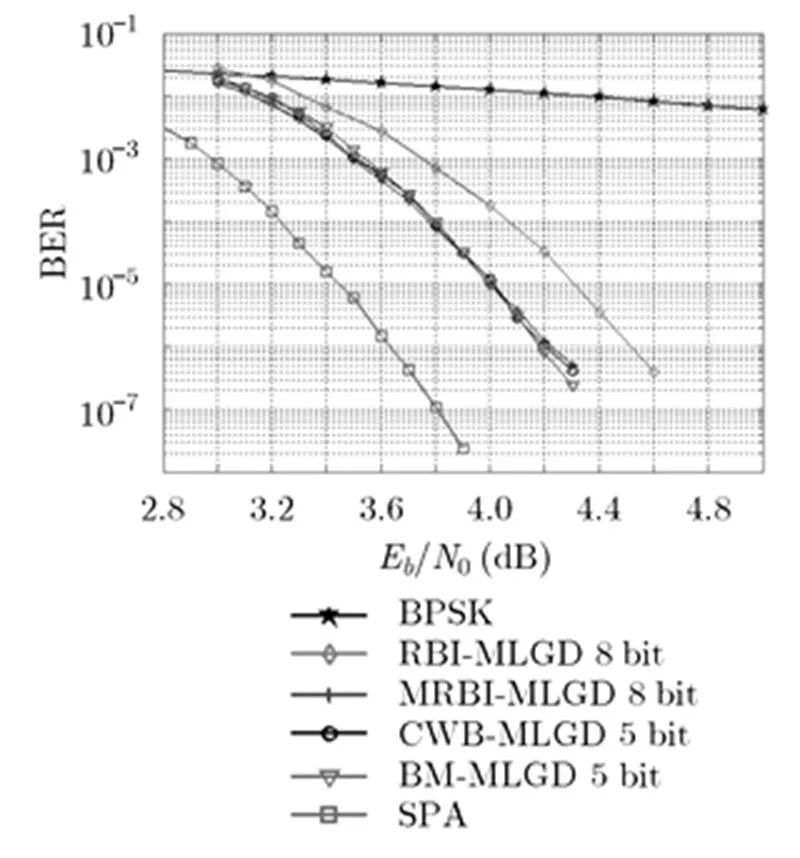
图4 (1023, 781) LDPC码译码性能

图5 (1023, 781) LDPC码译码收敛速度

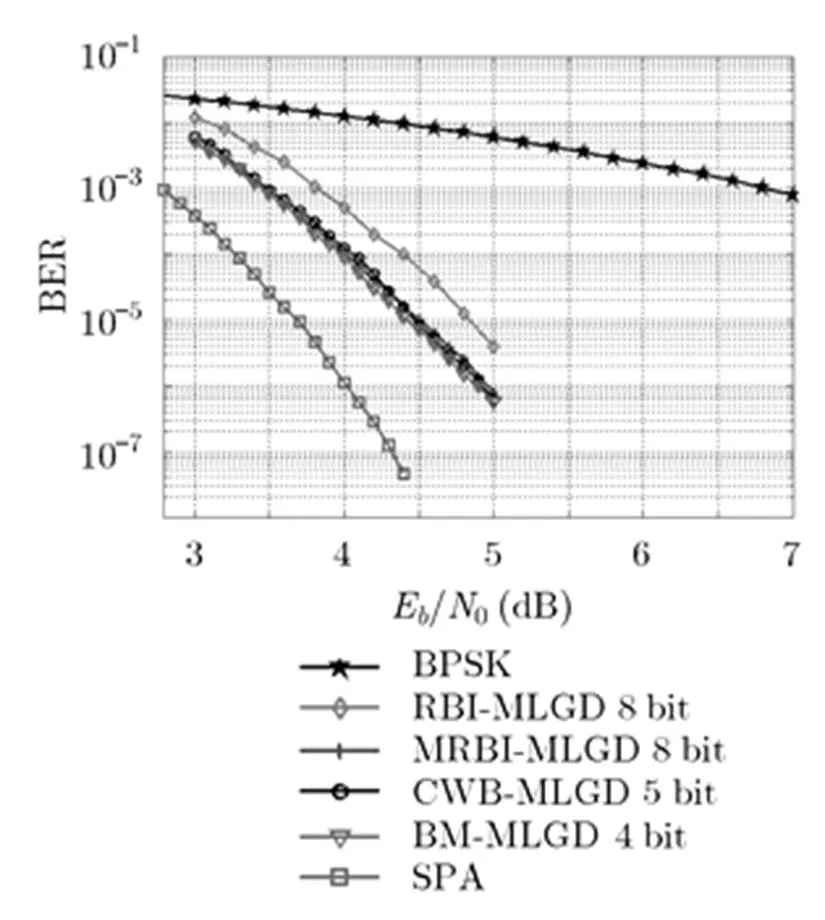
图6 (255, 175) LDPC码译码性能

图7 (255, 175) LDPC码译码速度

[1] GALLAGER R G. Low density parity check codes[J]., 1962, 8(1): 21-28. doi: 10.1109/ TIT.1962.1057683.

[2] CHEN X, KANG J, and LIN S. Memory system optimization for FPGA-based implementation of Quasi-cyclic LDPC codes decoders[J]., 2011, 58(1): 98-111. doi: 10.1109/TCSI.2010.2055250.

[3] GUTIERREZ F, GRACIELA C, MORERO D,FPGA implementation of the parity check node for min-sum LDPC decoders[C]. IEEE Conference on Programmable Logic,Bento Goncalves, 2012: 1-6. doi:10.1109/SPL.2012.6211802.

[4] KOU Y, LIN S, and FOSSORIER M. Low-density parity-check codes based on finite geometries: a discovery and new results[J]., 2001, 47(7): 2711-2736. doi: 10.1109/18.959255.

[5] HUANG Q, KANG J Y, ZHANG L,Two reliability-based iterative majority-logic decoding algorithms for LDPC codes[J]., 2009, 57(12): 3597-3606. doi: 10. 1109/TCOMM.2009.12. 080493.

[6] CATALA P J M, GARCIA F, VALLS J,Reliability-based iterative decoding algorithm for LDPC codes with low variable-node degree[J]., 2014, 18(12): 2065-2068. doi: 10.1109/LCOMM.2014.2363112.

[7] CHEN H, ZHANG K, MA X,Comparisons between reliability-based iterative min-sum and majority-logic decoding algorithms for LDPC codes[J]., 2011, 59(7): 1766-1771. doi: 10.1109/ TCOMM.2011.060911.100065.

[8] NGATCHED T M N, ATTAHIRU S, and JUN C. An improvement on the soft reliability-based iterative majority-logic decoding algorithm for LDPC codes[C]. Proceedings of 2010 IEEE Global Telecommunications Conference, Miami, USA, 2010: 1-5. doi: 10.1109/GLOCOM. 2010.5684111.

[9] 陶雄飞, 王跃东, 柳盼. 基于变量节点更新的LDPC码加权比特翻转译码算法[J]. 电子与信息学报, 2016, 38(3): 688-693. doi: 10.11999/JEIT150720.

TAO Xiongfei, WANG Yuedong, and LIU Pan. Weighted bit-flipping decoding algorithm for LDPC codes based on updating of variable nodes[J].&, 2016, 38(3): 688-693. doi: 10.11999/ JEIT150720.

[10] 陈海强, 罗灵山, 孙友明, 等. 基于大数逻辑可译LDPC码的译码算法研究[J].电子学报, 2015, 43(6): 1169-1173. doi: 10.3969/j.issn. 0372-2112.2015.06.019.

CHEN Haiqiang, LUO Lingshan, SUN Youming,Decoding algorithms for majority-logic decodable LDPC codes[J]., 2015, 43(6): 1169-1173. doi: 10.3969/j.issn.0372-2112.2015.06.019.

[11] ZHANG K, CHEN H, and MA X. Adaptive decoding algorithms for LDPC codes with redundant check nodes[C]. 2012 7th IEEE International Symposium on Turbo codes and Iterative Information Processing(ISTC), Gothenburg, 2012: 175-179. doi: 10.1109/ISTC.2012.6325222.

[12] RICHARDSON T J and URBANKE R L. The capacity of low density parity check codes under message-passing decoding[J]., 2001, 47(2): 599-618. doi: 10.1109/18.910577.

[13] TANNER R M. A recursive approach to low complexity codes[J]., 1981, 27(5): 533-547. doi: 10.1109/TIT.1981.1056404.

[14] LI X, QIN T, CHEN H,. Hard-information bit- reliability based decoding algorithm for majority-logic decodable non-binary LDPC codes[J]., 2016, 20(5): 886-869. doi: 10.1109/LCOMM.2016.2537812.

Binary Decoding Message Iterative Majority-logic LDPC Decoding and Its Quantizing Optimization

LI Xiangcheng①②③CHEN Haiqiang②③LIANG Qi②SUN Youming①③WAN Haibin②③QIN Tuanfa①②③

①(,,510640,)②(,,,530004,)③((),,,530004,)

A low complexity iterative majority-logic decoding algorithm is presented. For the presented algorithm, binary decoding messages are involved in the message passing, processing and updating process. Instead of computing the extrinsic information, the presented algorithm computes the reliability measure based on syndrome states (correct or error) in the Tanner graph. Compared with several existing iterative majority-logic decoding algorithms, the presented algorithm does not require the information scaling and hence can avoid the corresponding real multiplication operations. This leads to very low decoding complexity. Furthermore, a special quantization is combined with the presented algorithm. The optimization method is also given based on the discrete Density Evolution (DE). Simulation results show that, compared with the original algorithm, the presented algorithm can achieve about 0.3~0.4 dB performance gain over the Additive White Gaussian Noise (AWGN) channel. Moreover, all the decoding messages exchanged among the nodes are binary-based, which makes the presented algorithm convenient for the hardware implementations.

Decoding algorithm; LDPC codes; Majority-logic; Quantization; Syndrome message

TN911.22

A

1009-5896(2017)04-0873-08

10.11999/JEIT160563

2016-06-01；

改回日期：2016-11-25；

2017-01-22

覃团发 tfqin@gxu.edu.cn

国家自然科学基金(61261023, 61362010, 61661005)，广西自然科学基金(2014GXNSFBA118276)

The National Natural Science Foundation of China (61261023, 61362010, 61661005), The Natural Science Foundation of Guangxi (2014GXNSFBA118276)

黎相成： 男，1979年生，博士生，研究方向为信道编译码理论与技术.

陈海强： 男，1976年生，教授，研究方向为现代编码理论、协作通信.

梁 奇： 男，1991年生，硕士生，研究方向为通信与信息系统.

孙友明： 男，1975年生，博士生，研究方向为通信与信息系统.

万海斌： 男，1979年生，副教授，研究方向为无线通信理论与技术.

覃团发： 男，1966年生，教授，研究方向为多媒体通信理论与技术.