深海会聚区特征参数计算与分析

张晶晶 罗博

（第七一五研究所，杭州，310023）

深海会聚区特征参数计算与分析

张晶晶 罗博

（第七一五研究所，杭州，310023）

对深海声道会聚区形成的原因和条件、会聚信号的形成机理、会聚区特征参数的计算等进行了研究，以两种典型的深海声速剖面为例，计算了深海会聚区特征参数，并利用射线声学模型在深海夏季声速剖面情况下进行声线仿真，得到了特征参数随声源和接收点深度的变化规律，对声呐设备的设计及如何利用会聚区进行远程探测具有指导意义。

深海声道；会聚区；特征参数

SOFAR声道[1]中，声波的传播速度比其上层和下层都小，位于这一水层声源发出的声波，其声线将向水层中的声速极小值方向弯曲，声强很大，能传播相当远的距离。当海深满足一定条件时，声源发出的声能量，不经过海底和海面的反射和吸收，被限制在声道内部，形成声强很高的会聚区。深海会聚区现象是深海主要的水声环境特点之一，当会聚区现象发生时，声呐的作用距离将发生质的变化。利用深海会聚区现象实现远程探测将成为声呐最重要的工作方式之一。因此，深入研究深海会聚区现象形成的机理，实现会聚区特征参数的快速预报，对声呐系统的设计和使用具有至关重要的意义。

1 深海会聚区形成的原因和条件

在深海海域，由于海表面吸收太阳的能量，上层海水的温度比下层高，声速随温度的增加而减小，出现负声速梯度；到达一定的深度后，水温不变，形成深海等温层，但海水静压力却随着深度增加而增加，出现正声速梯度。在声速负梯度和声速正梯度交接处即声道轴处，出现声速极小值。在深海声道轴海域，声源在海表面附近以某出射角向海水中发射声线，根据声线传播规律，声线通过声道轴后逐渐向海面弯曲，最后折向海表面。在一定的距离和深度，声线会聚在一起，这个地方的声强特别强，形成深海会聚区。

由于海区声速分布非常复杂，为了研究方便，假设声速梯度分布为线性，gup为声道轴上层海水声速梯度，gd为声道轴下层海水声速梯度，c0为海表面声速，h0为声道轴深度，ch为声道轴处声速，hl为声道临界深度，chl为声道临界深度处声速，med为深度余量，h为海底深度，α为声线初始掠射角。要形成深海会聚区，需要满以下两个条件：

（1）海水声速分布必须形成声道型声速梯度

声道型声速梯度是指形成海水声道必须具备的声速梯度，即上层海水为负梯度，下层海水为正梯度，两层之间出现声速极小值，即必须满足：

（2）海水深度大于临界深度并有余量

要出现会聚区，除了声速分布符合声道型特征外，对海底深度也有一定的要求。当海底深度大于临界深度，并留有一定深度余量时，下层向上层弯曲的声线就不会碰触海底并反转弯向声速极小值方向，从而形成完整的声道，在海表面形成会聚区。当海底深度小于声道临界深度时，下层向上弯曲的声线就会触碰到海底，一部分声波被海底反射，另一部分声波会被海底吸收，从而导致声强度下降，声波传播距离减小，于是在海表面难以形成会聚区。这表明，对于给定的声速分布一定会有个产生会聚区的最小海区深度余量，并且这一深度余量与表面声速有一定的依赖关系，当深度余量超过几百米时，会聚区有可能出现，即必须满足[2]：

2 会聚信号的形成

声速沿深度的分布是任意的，这时可以将声速分布分为许多层，使各层都具有恒声速梯度。于是，声线在各层中所通过的路径都将是圆弧（声速梯度不为零的情况）或直线（声速梯度为零， 即均匀层的情况）。

设将海洋中的声速分布分为n层，各层的厚度为hi，各层上、下界面的声速值为ci−1和ci（i=1，2，…n）。第一层的上界面为海面，其声速为c0，第n层的下界面为海底，其声速为cn。假设声源和接收器都置于海面(即c=c0界面)上，出射角为α0的声线由于深海声道的作用，在第j层的分界面上反转，则它完成一个反转时在各层中所经过的水平距离为di，并且[3]

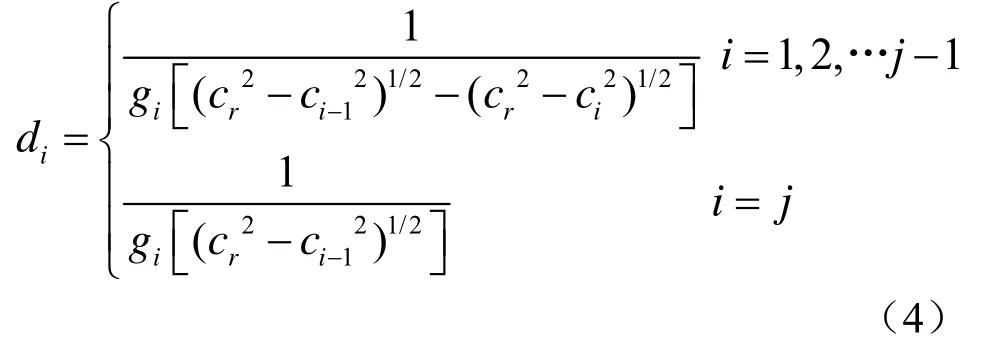
上式中，cr称为给定声线（具有出射角α0的声线）的特征参数，它等于该声线在反转深度上的声速。

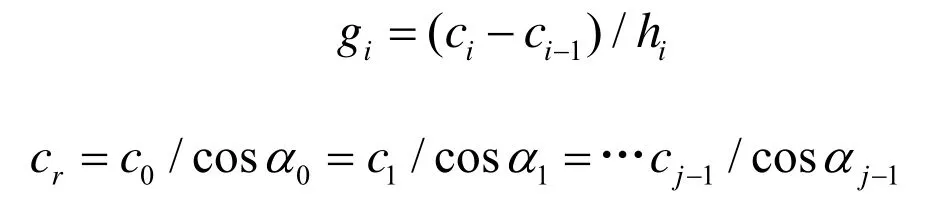
显然，形成会聚区，除存在声速极小值外，还必须保证至少水平角度出射的声线，能在海底平面反转，这就要求

从无方向性声源发出的无数声线中，只有那些cr＜cn的声线，才对会聚区声场有贡献。由此可以得到形成会聚区的最大声源出射角为：

对于那些cr＞cn的声线，将经过海底反射，形成海底反射传播途径。

如果在第一层中c1＜c0，即表面层为混合层声道，则只有那些cr＞c1的声线，才对会聚区声场有贡献。由此可以得到形成会聚区的最小声源出射角为：

对于那些cr＜c1的声线，被限制在混合层声道中，形成混合层声道中直达声传播途径。

设有一声线与α0相邻近，其出射角为，它完成一个反转时在各层中所通过的水平距离为，且与式（4）表示的di有相同的形式。将的表示式对小量Δ做泰勒展开，略去高次项，有[3]：

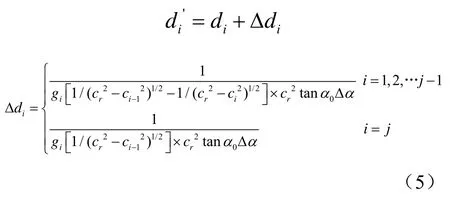
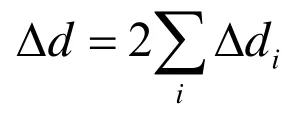
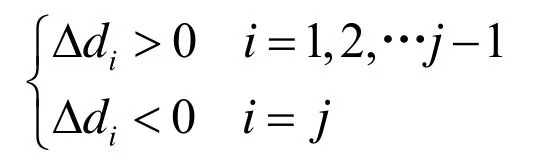
3 会聚区特征参数计算模型

3.1 会聚区距离

当接收器不是与声源同深度，而是任意深度，例如处于第p层，离第p层上界面距离为zk时，会聚区出现的距离按式（7）计算[3]。

3.2 会聚增益

形成会聚区的聚焦因子，由下式给出[3]：

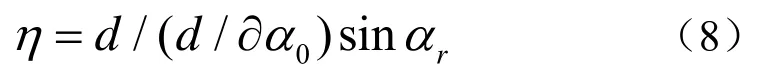
由di的表达式（4）可得：

根据Δdi的表达式（5）可得[3]：

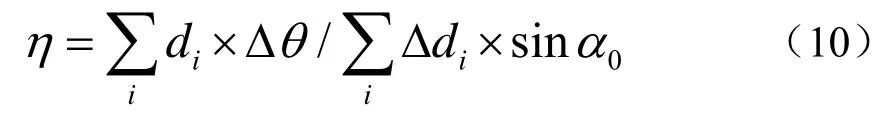
4 计算与仿真分析

根据前面的分析可以看出，会聚信号出现的距离，取决于声道轴的位置、声速分布、发射深度、接收深度以及形成会聚区的出射角的大小等因素。在深海冬季和深海夏季两种典型的深海声速分布情况下，对声源和接收器在不同深度时第一会聚区参数进行计算，并利用射线声学模型在深海夏季声速剖面情况下进行声线仿真，分析声源和接收器在不同深度时对会聚区形成的影响。

4.1 深海冬季类型

海面声速为c0，由浅至深声速梯度分别为g1，g2和g3。h1=100 m，h2=1 000 m。

图1 深海冬季类型声速剖面

假设声源和接收器同深度h，根据第3节公式计算不同深度时会聚区出现的距离d、会聚区宽度Δd、聚焦增益η和相应的出射角α。会聚区距离随深度的变化关系如图2所示。会聚区宽度随深度的变化关系如图3所示。会聚增益随深度的变化关系如图4所示。相应出射角随深度的变化关系如图5所示。各参数具体数值见表1。

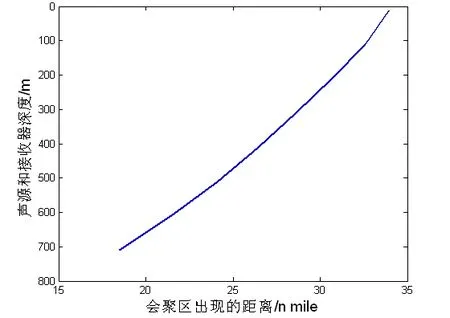
图2 会聚区距离与深度的依赖关系（深海冬季）

图3 会聚区宽度与深度的依赖关系（深海冬季）

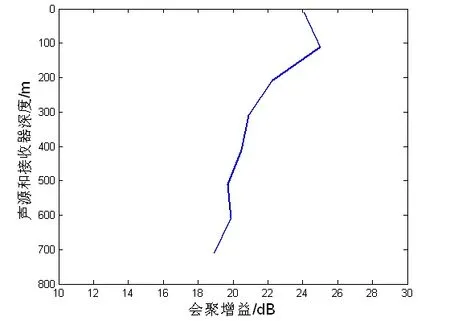
图4 会聚增益与深度的依赖关系（深海冬季）

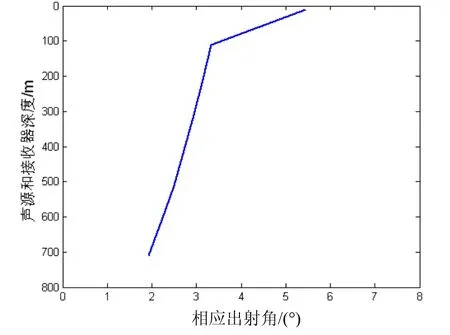
图5 出射角与深度的依赖关系（深海冬季）

表1 不同深度条件下会聚区参数表（深海冬季）

4.2 深海夏季类型

海面声速为c0，由浅至深声速梯度分别为g1，g2和g3。h1=100 m，h2=1 000 m。

图6 深海夏季类型声速剖面

假设声源和接收器同深度，根据第3节公式计算不同深度时会聚区出现的距离、会聚区宽度、聚焦增益和相应的出射角。会聚区距离随深度的变化关系如图7所示。会聚区宽度随深度的变化关系如图8所示。会聚增益随深度的变化关系如图9所示。相应出射角随深度的变化关系如图10所示。各参数具体数值见表2。

图7 会聚区距离与深度的依赖关系（深海夏季）

图8 会聚区宽度与深度的依赖关系（深海夏季）

图9 会聚增益与深度的依赖关系（深海夏季）

图10 出射角与深度的依赖关系（深海夏季）

表2 不同深度条件下会聚区参数表（深海夏季）

以上两种声速分布的理论计算结果基本一致。根据理论计算结果，可以看出：（1）随着深度的增加，越靠近声道轴，会聚区出现的距离越近；（2）随着深度的增加，越靠近声道轴，会聚区的宽度越大；（3）越靠近声道轴，会聚区宽度增大，汇聚增益减小；（4）随着深度的增加，相应的出射角基本呈减小趋势。

以深海夏季典型的声速剖面为例，利用射线声学模型对两种不同声源与接收器深度下的声线进行仿真，仿真结果如图11和图12所示。图11是声源和接收器位于100 m深度时的声线图，从图中可以看出会聚区出现的距离为62.3 km（33.8 n mile），会聚区宽度是2.5 km（1.4 n mile）；图12是声源和接收器位于500 m深度时的声线图，从图中可以看出会聚区出现的距离为46.8 km（25.3 n mile），会聚区宽度是12.7 km（6.9 n mile）。仿真结果与表2中理论计算结果吻合。由图11和图12可见，随着声源和接收器深度变深，会聚区出现的距离越来越近，会聚区宽度越来越宽，声线仿真结果与理论计算结论一致。

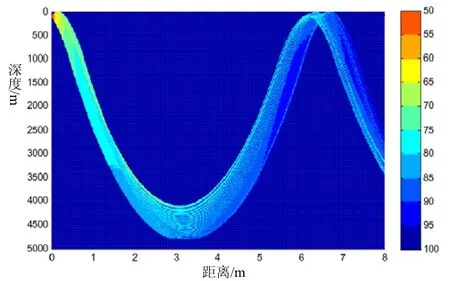
图11 声源和接收器深度100 m

图12 声源和接收器深度500 m

5 结论

本文分析了深海声道会聚区形成的原因和条件、会聚信号的形成机理、会聚区特征参数的计算等，并利用射线声学模型在深海夏季声速剖面情况下进行声线仿真，得到了第一会聚区特征参数随声源和接收点深度变化的规律。该规律对低频可变深声呐设备的设计及如何利用第一会聚区进行远程探测具有实际指导意义。本文通过理论分析和仿真验证得出的结论，后续将通过海试进行验证。

[1]刘伯胜,雷家煜.水声学原理[M].哈尔滨:哈尔滨工程大学出版社,1997.

[2]徐清华,彭小宏,傅调平,等.舰艇机动穿越深海会聚区对潜艇探测研究[J].指挥控制与仿真,2014,36(2):18-21.

[3]薛福茹.深海声道会聚区的研究[J].舰船科学技术,1982,(1):46-58.