一种高阶MFB高通有源滤波器相位调节方法
施彤云
(第七一五研究所,杭州,310023)
一种高阶MFB高通有源滤波器相位调节方法
施彤云
(第七一五研究所,杭州,310023)
提出一种基于MFB结构的六阶切比雪夫高通有源滤波器的设计方法,从滤波器传递函数考察相位-元件敏感度关系,探讨一种工程上切实可行的相位调节方法。测试结果证明,该方法可满足多通道应用场合对滤波器相位一致性较高的要求。
六阶切比雪夫;MFB有源滤波器;相位-元件敏感度关系式;相位调节
随着电子技术的发展,模拟有源滤波器的设计技术已经非常成熟,大量的文献资料可供设计者参考,并出现了多款模拟有源滤波器设计软件,大大降低了这类电路的设计门槛和难度。但由于实际使用元器件精度和容差的影响,想要制作出一款高质量、高性能、且与设计指标高度吻合的模拟有源滤波器并非易事。某些场合下,需要对元件值进行微调才能使电路满足指标要求。
本文从一种基于 MFB电路结构的六阶切比雪夫高通有源滤波器设计实例入手,从滤波器传递函数出发,考察相位-元件敏感度关系,讨论了产生多个滤波器之间相位不一致性的成因及其敏感程度,通过数值计算方法总结规律,提出并实践了一种相位调节方法,使得滤波器适用于阵列应用中对相位一致性要求较高的场合。实际经验表明,该方法切实可行,成本和复杂度均在可接受范围内。
1 滤波器设计
滤波器主要指标有:高通滤波器,单位增益,截止频率100 Hz, 50 Hz衰减不小于40 dB,带内纹波不大于1 dB,多个滤波器之间通带内相位不一致性不大于4°。
滤波器元件参数设计并不复杂,可以有多种手段设计出多种形式的滤波器,本文利用现有的滤波器软件设计。TI(Texas Instruments Incorporated)曾经发布过一款免费的有源滤波器设计软件FilterPro,借助该软件,可以快速地设计出所需滤波器的电路形式、元件参数、滤波器频响特性评估等[1]。
将滤波器指标输入到软件,并适当调整元件参数到合理范围,可快速得到6阶MFB高通0.5 dB纹波的切比雪夫有源滤波器电路。电路由3级相同拓扑结构的二阶节串联而成,如图1所示。每个二阶节具有相同的电路结构,其中二阶节电路如图2所示,3级电路参数见表1[2]。

图1 滤波器级联框图

图2 二阶节电路图
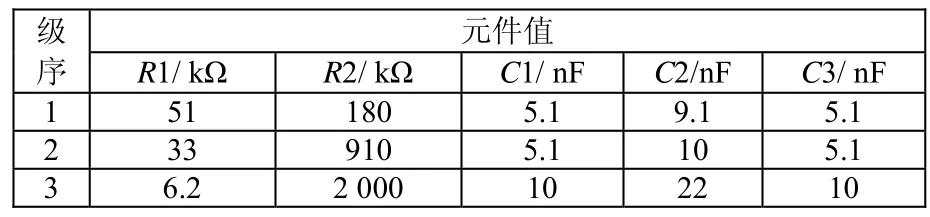
表1 3级二阶节元件参数列表
滤波器幅频特性和相频特性曲线则如图3所示。1 kHz处增益0.14 dB,带内起伏小于0.4 dB,50 Hz处衰减达51.5 dB,设计符合初始要求。
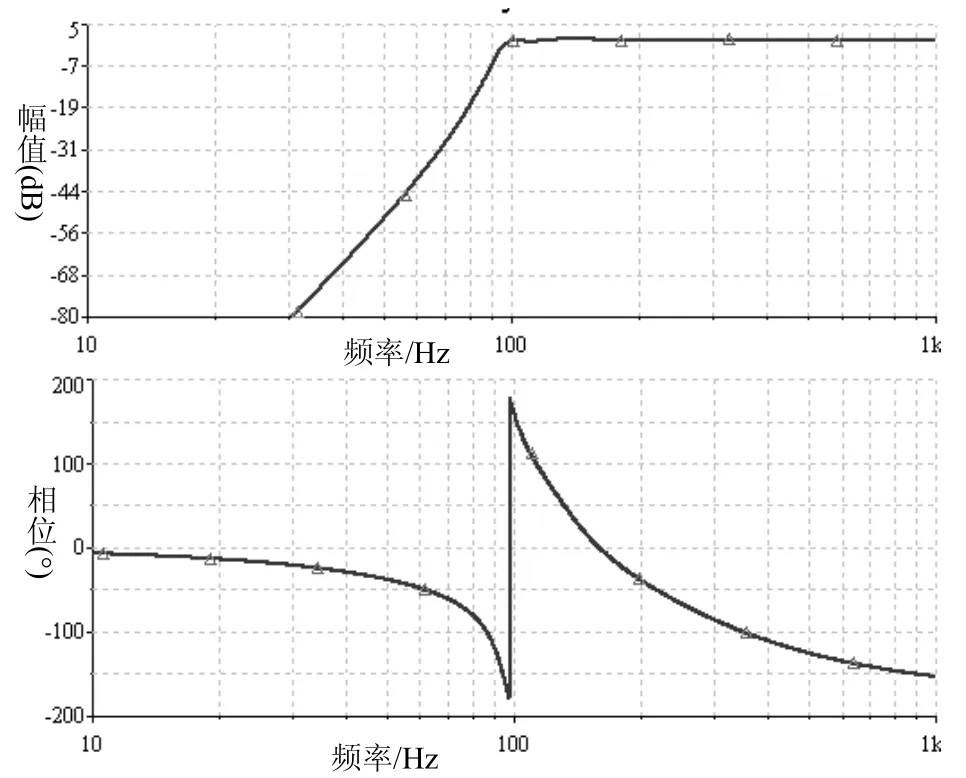
图3 滤波器幅-相频特性
2 滤波器相位敏感性分析
图3所示相频特性曲线中,在100 Hz拐点频率附近滤波器相位变化剧烈,其相频曲线斜率陡峭,因而在该频率附近,多个滤波器之间想要实现相位一致,对元器件一致性要求很高。以图2所示一个二阶节为考察对象,可得到电路传递函数[3]

用jω代替s即得到电路的频率特性,并由此可得到其幅频特性和相频特性表达式:
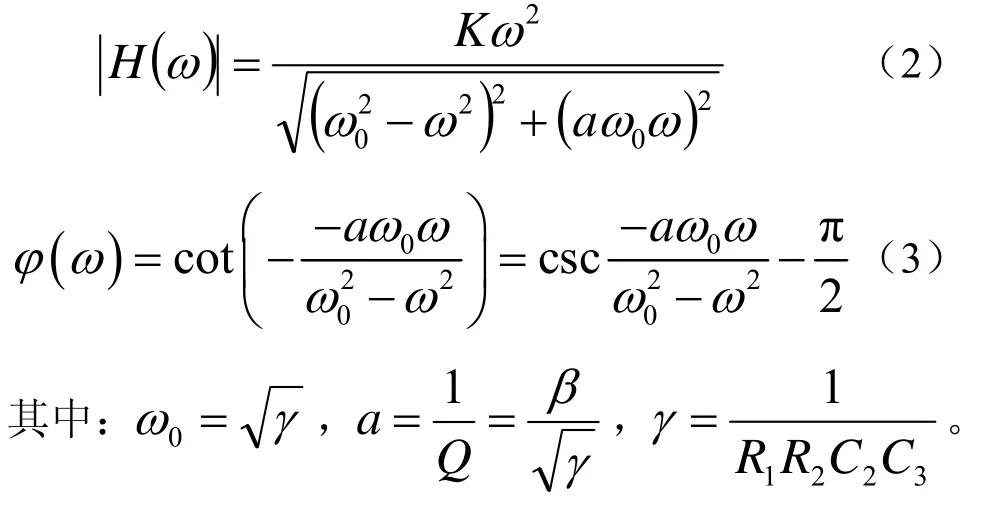

则相位敏感度定义为:

按照式(5)定义,对式(3)求全微分可得到滤波器相位与各元器件偏差之间的比例关系。对式(3)求电阻电容偏导数得到的表达式极为庞大复杂,含有多个变量,直接从表达式得到敏感度变化规律是困难的,但是通过数值计算,可以较为直观地看到相位与各元器件容差之间的比例关系。
电路采用表1所列元件值,计算100 Hz处3级二阶节相位敏感度如表2所示。二阶节敏感度数值计算Matlab程序如下[4]:


表2 3级二阶节敏感度比例
由表2可以看出,除了第3级的C1以外,其余敏感比例关系一致,即元件值增大,相位减小。如果选择电阻精度±0.1%,电容精度±1%来制作滤波器,先从单极性偏差,在原程序基础上增加元件误差可以计算出100 Hz拐点频率附近3级二阶节串联后滤波器相位与理论相位最恶劣偏差见表3。

表3 100 Hz附近元件误差引起的相位最大偏差
很明显,即使按照元件值的单极性偏差计算,表3所列最大相差也超过了指标要求4°的目标。因而,想要在所选元件精度范围内制作出相位一致性符合要求的多个滤波器电路,还需要一种调整手段对相位进行微调,使得多个滤波器电路的相位控制在一个可接受的偏差范围内。
3 相位微调方法及实验结果
实际电路中,各元器件误差分布是不确定的,定位到偏差最大的那个元件并对其进行修正是不现实的。但是考察图4所示的3个二阶节的相频特性曲线,可以看出相互之间并不相同。其中第二级φ2(ω)相位特性在 100~200 Hz范围内变化斜率和变化幅度最大,结合表3所示的最大相位差规律,可以尝试选择第2级电路参数调节来实现整个滤波器相位的微调。

图4 3个二阶节的相频特性
采用表1所列元件值,通过数值计算100~200 Hz范围内几个频点处第 2级二阶节相位敏感度见表4。由表4可以发现,相位对C1的敏感度最小,其它四个元件敏感度比较接近,而R1敏感度在除了100 Hz以外其它位置的变化规律与表3的变化规律接近,因而尝试通过R1的微调来修正整个滤波器的相位偏差。

表4 第2级各频点敏感度比例
图5为利用Matlab、手动微调R1得到的相位偏差修正的结果。其中相位差指的是滤波器在元件偏差时相对无偏差时的相位差。图中,当电阻存在±0.1%、电容存在±1%最大偏差时,频率低于170 Hz以下的相位差均超过±2°,但是对滤波器第二级的R1作5%范围内的微调后,可将除了100 Hz以外其他频率点的相位差调整到±2°范围内。微调R1对相位修正,Matlab计算程序如下:

而元件值的微调对幅频特性的影响较小,完全处于可接受范围内。图6为微调元件值后的幅频特性曲线与理想元件值幅频特性曲线的对比,元件值微调前后带内幅频误差不超过±0.5 dB。
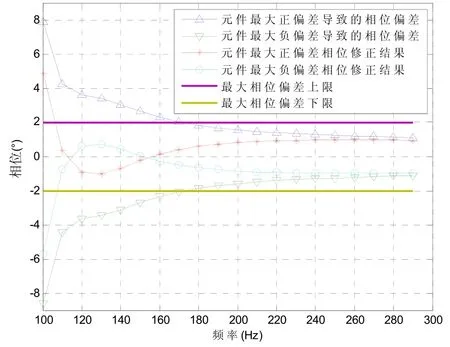
图5 微调R1得到的相位修正结果

图6 微调R1对幅频特性的影响
实际滤波器电路试制与调试验证,上述方法具有工程可实现性。表5所示为27块6阶MFB高通切比雪夫滤波器相位一致性调整和测试结果,所调试的 27块电路一致性全部满足指标±2°要求范围内,同时其幅频特性满足带内纹波不大于1 dB、通道间不一致性不大于1 dB的指标要求。表5中最大(最小)相移是指 27块滤波器的输出信号与输入信号之间的最大(最小)相位偏移,相移范围即为27块滤波器在某一频点的相位一致性。
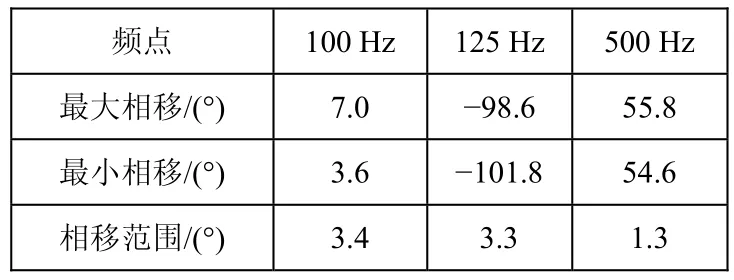
表5 27块滤波器相位一致性测试结果
4 结论
本文讨论的高阶滤波器相位敏感度分析和微调方法,通过实践验证具有工程可实现性和可重复性,并具备一定的推广价值。在应对不同阶数、不同电路结构、不同传递特性的有源高通、有源低通滤波器的相位控制时,均可借鉴本文所述方法。
[1]Texas Instruments,Inc.FilterPro Desktop Help[Z].2010.
[2]约翰逊D E,约翰逊J R, 穆尔H P,等.有源滤波器精确设计手册[M].李国荣,译.北京:电子工业出版社,1984.
[3]DELIYANNIS T,SUN Y,FIDLER J K.Continuous-time active filter design [J].Journal of the Audio Engineering Society[J].1998,22(10):770-782.
[4]刘正君.Matlab科学计算与可视化仿真宝典[M].北京:电子工业出版社,2009.

