基于主成分追踪方法的过程监测

潘怡君，杨春节，孙优贤，周哲，安汝峤



基于主成分追踪方法的过程监测

潘怡君，杨春节，孙优贤，周哲，安汝峤

(浙江大学控制科学与工程学院，浙江杭州，310027)

为了将主成分追踪（PCP）的方法应用在工业系统过程监测中，提出一种基于均值方差的过程监测统计量。首先将标准化后的训练以及测试数据矩阵进行PCP分解，然后分别计算分解得到的稀疏矩阵中每个变量的均值和方差，并进行比较，最后将它应用在数值仿真和TE过程中。研究结果表明：这种统计量能够消除大部分噪声的影响。使用这种统计量能够同时完成模型建立、故障检测、故障识别以及过程重构这4个过程监测的步骤，具有较好的适用性。

过程监测；主成分追踪；TE过程；均值方差

工业过程生产是国家经济发展的支柱产业，因此保证生产过程的高效性和稳定性十分重要。工业过程监测方法分为3类：基于定量数学模型的方法、基于知识的方法以及基于数据驱动的方法[1−3]。相比于基于机理模型和基于知识的方法，目前应用较多的是基于数据驱动的过程监测方法。这类方法不需要构建精确的过程机理模型，也不需要丰富的专家经验知识。它是以实际生产中采集到的大量数据为基础，利用数据潜在的特性，进行过程监测[4]。目前应用较多的数据驱动方法有主元分析(PCA)、偏最小二乘(PLS)、支持向量机(SVM)、人工神经网络(ANN)以及在它们基础上面研究出来的改进方法[5]。近年来，一种基于主成分追踪(PCP)的算法被提出。2011年，CANDES等[6−11]介绍了PCP算法的原理及求解方法。他们通过解决凸优化问题将数据矩阵分解成低秩矩阵和稀疏矩阵2个部分。其中低秩矩阵为没有传感器噪声和过程故障的数据，稀疏矩阵中的数据包含传感器噪声以及过程故障。目前，主成分追踪的方法大多应用在视频监控领域，BOUWMANS等[12]对PCP在视频监控领域的应用情况进行了综述。ISOM等[13]将PCP的算法应用在过程监测中，提出PCP方法能够同时完成模型建立、故障检测、故障分离和过程重构，然后从上面4个方面计算了PCA和PCP的关系，并利用这种关系应用PCP进行过程监测。CHENG等[14]验证了PCP方法相比于PCA，对过程中出现的异常值不敏感的特性，以及在进行PCP运算前对数据进行归一化处理的必要性，最终通过观察故障数据的稀疏矩阵中的元素幅值变化来进行过程监测。PCA将数据分为主元空间数据和残差空间数据，而PCP将数据分为低秩矩阵数据和稀疏矩阵数据。虽然二者相似，但是不能直接完全地把PCA的统计量应用在PCP中。这是因为PCA方法的本质在于降维[15]，而PCP是进行矩阵分解，保持矩阵维数不变。同时，由于噪声出现的随机性，若观察单个采样时间的变量数值，可能会导致比较高的误报率。因此，本文作者提出了一种基于均值方差统计指标的过程监测统计量。利用均值和方差是因为均值和方差均为表现过程统计信息的变量。方差利用数据的偏离程度能在均值的基础上进一步表现数据统计特性。它是通过计算训练集和测试集的稀疏矩阵中变量的均值方差得到的过程监测统计量，利用一段时间的统计指标来进行过程监测，可以在一定程度上避免单个时刻噪声的干扰。本文首先说明了低秩矩阵中不应该包含传感器噪声以及过程故障。其次说明利用新的统计量能够同时实现过程监测的4个步骤。并且可以实现多个故障分离识别。而且由于训练集稀疏矩阵中包含的是传感器噪声，而测试集稀疏矩阵中包含传感器噪声和过程故障，二者相差的为过程故障，构建这样的统计量还避免了应用其他数据驱动方法构建统计量时，有噪声干扰的问题，可以提高过程监测的精确度。最后分别在数值仿真和TE模型上面进行了仿真，验证了统计量的可用性。

1 主成分追踪

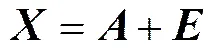
式中：为低秩矩阵，为去除传感器噪声和过程故障的数据矩阵；为稀疏矩阵，仅仅包含传感器噪声以及过程故障的数据矩阵，因此指的是变量在第个样本点时，不存在传感器噪声以及过程故障。PCP的本质是解决如式(2)所示的凸优化函数，在本文中利用奇异值阈值的方法来解决这个矩阵分解的凸优化函数[16]。

(2)

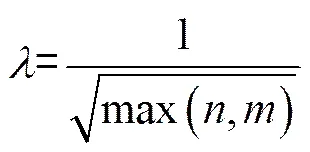
2 利用主成分追踪的方法进行过程监测

过程监测一般分为4个步骤，分别是模型建立、故障检测、故障分离以及过程重构。目前在过程监测研究中，大部分使用数据驱动的方法，但是PCA，PLS，ANN和SVM以及在它们基础上改进的方法都不能同时完成过程监测的4个步骤[17]。而PCP与它们相比，最重要的优点就是可以同时实现模型建立、故障检测、故障分离以及过程重构[13]。虽然在应用中，PCP暂时不能像PCA和PLS那样进行在线实时监测，但是它可以同时实现过程监测的4个步骤。因此，它的这种优点能够降低计算的复杂度，降低成本，更简洁地同时实现发现故障，识别故障引起的原因，恢复正常工况这些过程监测步骤。根据PCP的原理，可以得知数据矩阵被分解为2部分，分别是不包含传感器噪声和过程故障的低秩矩阵以及包含传感器噪声和过程故障的稀疏矩阵。

在实际的工业生产中，各个变量是具有相关性的。因此只有在传感器测量过程中没有噪声干扰时，才能得到变量具有相关性的数据，也就是低秩矩阵。例如给定1个矩阵，的秩为1，此时对第1个采样点的第1个变量加入传感器噪声，得到的新数据矩阵，此时的秩为2。由于噪声和故障具有随机性，出现的时间和变量均是不可控的，同时考虑前面提及的二维数据在某个时刻对某个变量引入噪声会改变变量之间的相关性，因此，推广到多变量过程中，噪声和故障的出现也一定会改变矩阵中列之间的相关性。这也说明PCP算法分解得到的低秩矩阵中不应该包含传感器噪声，因为包含传感器噪声和过程故障的数据不可能是低秩的。相对而言，稀疏矩阵中包含的就是传感器噪声以及过程故障，所以，利用稀疏矩阵来进行过程监测是可行的。在使用数据驱动方法进行过程监测时，需要使用2类数据集，分别是训练数据集以及测试数据集。考虑到PCP的原理，对训练数据集进行矩阵分解时，得到的稀疏矩阵1中应该只包含传感器噪声，而在对测试数据进行矩阵分解时得到的稀疏矩阵2不仅包含传感器噪声，还包含过程故障。因此，当稀疏矩阵2的数据分布情况和稀疏矩阵1情况不同时，即2的相关统计量超出了1的统计线，就完成了监测故障或异常状况的工作。虽然均值和方差反映的是一段时间之内数值的平均水平，但是故障的发生不会在某一个很短的时间段就消失，若这个时间段的均值出现了异常，不符合正常工况下的标准，则可以利用均值方差这些基本数据统计量对过程进行故障检测判断。使用这种统计量不仅能实现同时完成过程监测的4个步骤，而且计算简单，同时，在理论上能够基本消除过程中传感器噪声的 影响。

2.1 模型建立

在实际工业生产过程中，不同变量的数据幅值可能存在很大的不同，甚至有的会相差好几个数量级。因此，若在建立模型前没有进行归一化处理，则会对最后的结果产生很大的影响。虽然从表面上来看，对于PCP来说，不论是矩阵的秩还是矩阵的稀疏性，和归一化都没有关系，不会因为矩阵的归一化而改变它们的值。但是CHENG等[14]证明了在应用PCP方法之前对数据进行归一化的必要性。

因此，在模型建立之前，首先对训练集数据和测试集数据进行归一化处理。在本文中，采用最常用的均值、方差归一化方法。将归一化处理之后的训练数据矩阵和测试数据矩阵分别利用PCP方法进行矩阵分解，得到

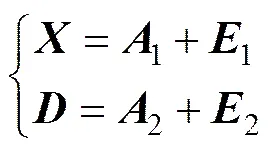
式中1为训练集的低秩矩阵；1为训练集的稀疏矩阵；2为测试集的低秩矩阵；2为测试集的稀疏矩阵。

至此，模型建立完成[16]。

2.2 故障检测

根据2.1节中建立的模型，首先计算矩阵1的统计量特性，均值和方差。在矩阵1中，计算每个变量一段时间内样本点的均值和方差。理论上，在得到训练集样本的统计特性之后，将2中每个变量每个时刻的值与训练集相应变量的均值相比较，若发现大于，则说明有故障发生。但是，由于噪声的干扰，为了防止出现错报，应考虑比较测试集样本在一段采样时间内的变量均值和方差。与训练集相比较，观察是否出现故障，进行故障检测。时间段的选取根据研究对象来确定。

2.3 故障识别

在本文中，计算测试集样本每个变量在一段时间内的均值和方差，与训练集样本得到的正常情况下的均值和方差比较，若变量的统计特性超出了正常阈值，则说明该变量导致了故障的发生，完成了故障识别。并且如果多个变量均超出正常阈值，还能够实现多重故障识别。

2.4 过程重构

无论是模型建立、故障检测还是故障识别，目的都是为了及早发现故障，并快速改正以消除故障，因此，过程监测的前3个步骤均是为过程重构做准备。过程重构就是根据已受故障影响的过程变量测量值估计出名义上的正常测量值*。在本文中，过程重构出的矩阵就是测试集样本D通过PCP算法分解得到的低秩矩阵2。

从前面可以得知：利用新提出的统计量能够同时完成模型建立、故障检测、故障识别以及过程重构这4个过程监测的步骤。下面利用数值仿真例子和实际的工业生产模拟实例TE过程来验证一下这种统计量的有效性。

3 仿真验证

在仿真验证中，数值仿真的测试集有500个样本，TE过程的测试集故障数据有800个样本。采样个数较少，因此，在故障检测阶段，每个变量均是对所有样本时间计算均值方差。因为PCP算法的局限性，在本文中采取计算每个变量所有样本点的均值方差，并且由于导致故障出现的变量具有不确定性。因此，本文中利用这个统计量进行故障检测只能判断是否出现故障，不能计算误检率和漏报率。

3.1 数值仿真

为了验证经过PCP算法分解得到的稀疏矩阵包含过程故障以及本文提出的统计量的可用性，首先在数值仿真例子上进行研究证明。在数值仿真例子中，由于数值矩阵里面的元素存在负数，所以稀疏矩阵中也可能存在负数。因此，在求解均值时，可能会出现相互抵消的情况，与实际情况不同，可能会降低故障幅值，会导致漏报。因此，在数值仿真例子中，均先对稀疏矩阵进行绝对值运算，再进行统计量均值和方差的求解。

ALCALA等[18]构建了一个数值仿真模型来验证统计量的有效性。因此，在本文中也利用这个数值仿真模型。过程模型如下式所示。

式中：1，2和3分别为零均值，标准差为1.0，0.8和0.6的随机变量；为零均值，标准差为0.2的正态分布噪声。得到故障样本的公式如下：

(6)

从得到的测试集稀疏矩阵2可以看出：在每个采样时刻变量1的幅值明显比其他变量的大，这说明对测试集利用PCP的方法进行矩阵分解得到的稀疏矩阵的确包含过程故障。同时，为了验证这个结论，还进行了其他变量发生故障的实验，均可以发现出现故障的变量在稀疏矩阵里面的幅值要比其他变量的大。图1和图2所示分别为对训练集和测试集的稀疏矩阵的所有样本点求取均值和方差相比较的仿真图。从图1和图2可以得出：测试集发生故障的变量1的均值1=0.633 8，1=0.028 8，训练集变量1的均值2= 0.096 7，2=0.019 6，1＞2，1＞2，因此，根据前面已经得到的稀疏矩阵特性，得出此时有故障发生。同时由于只有变量1的均值和方差，测试集比训练集大，因此，可以知道是变量1导致了故障的发生。同时测试集分解得到的低秩矩阵为没有过程故障的正常数据，完成了过程重构。通过分析图1和图2可知：利用PCP能很好地进行过程监测，并且利用均值和方差这2个统计量能够进行故障检测和故障识别，说明了这种新的统计量适合PCP算法的，并且能进行过程监测。

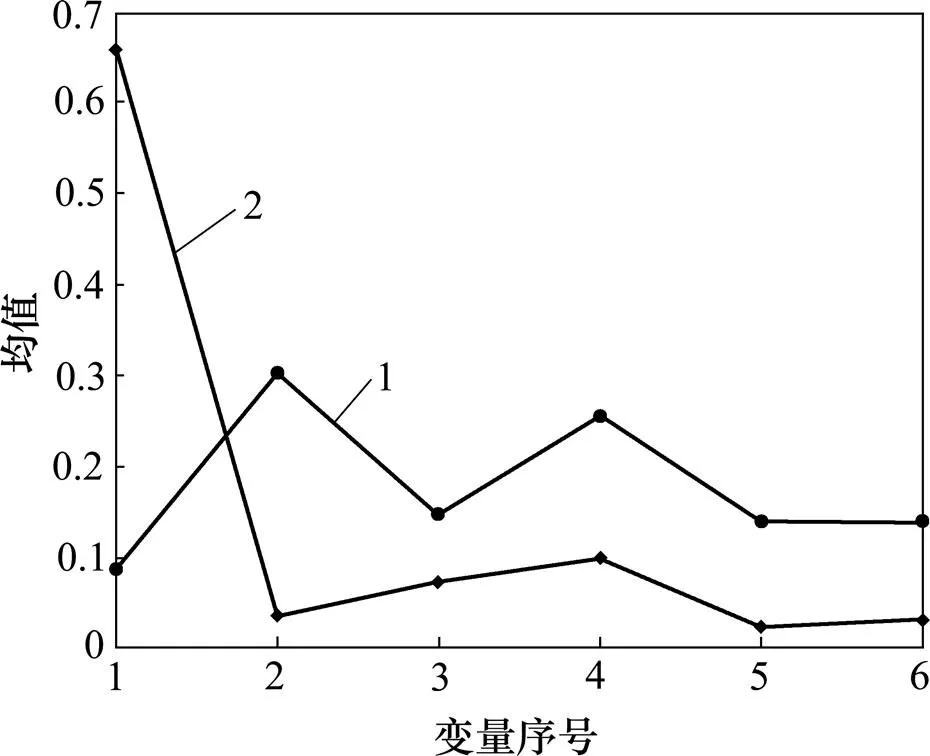
1—训练集统计量；2—测试集统计量。

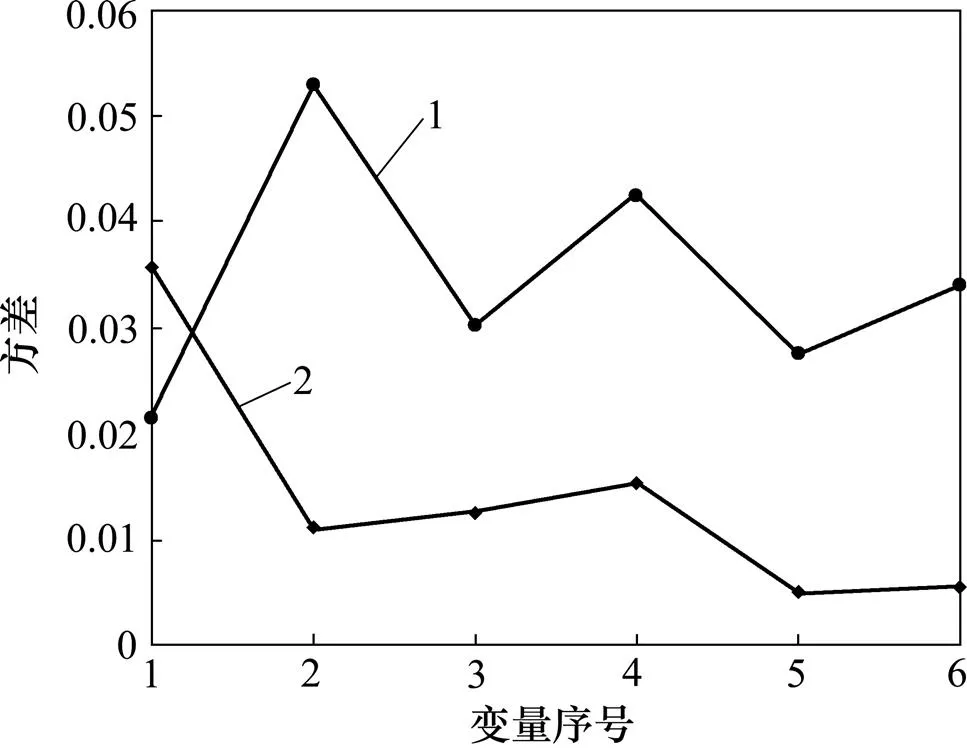
1—训练集统计量；2—测试集统计量。

为了更好地说明稀疏矩阵包含过程故障，以及这种统计量的监测效果。将变量1，3和4均引入故障，监测效果如图3和图4所示。

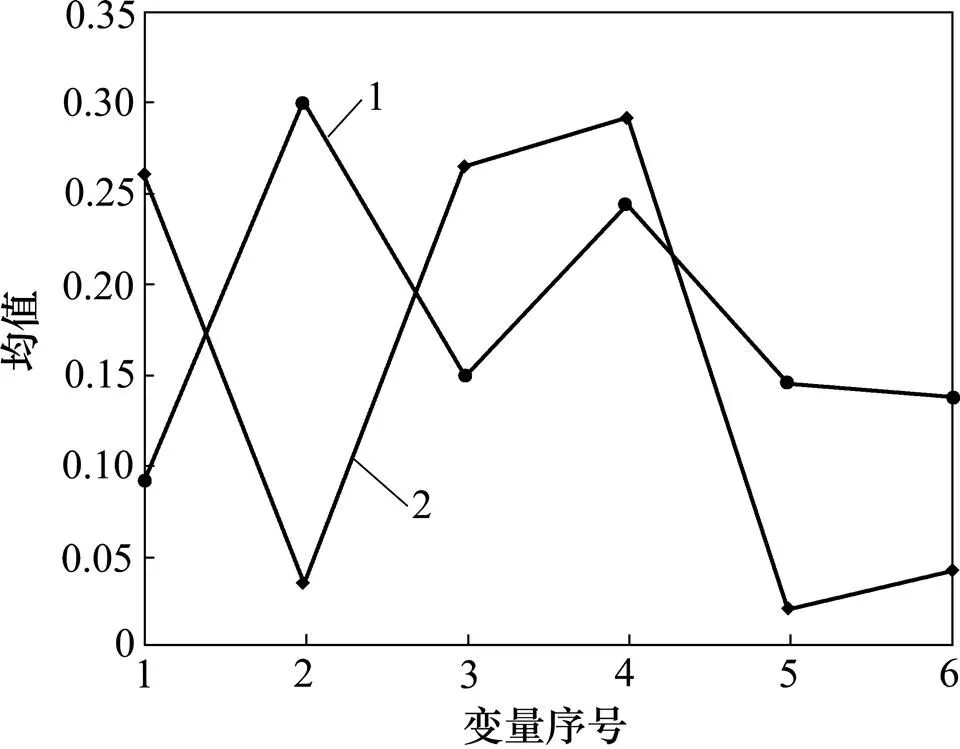
1—训练集统计量；2—测试集统计量。

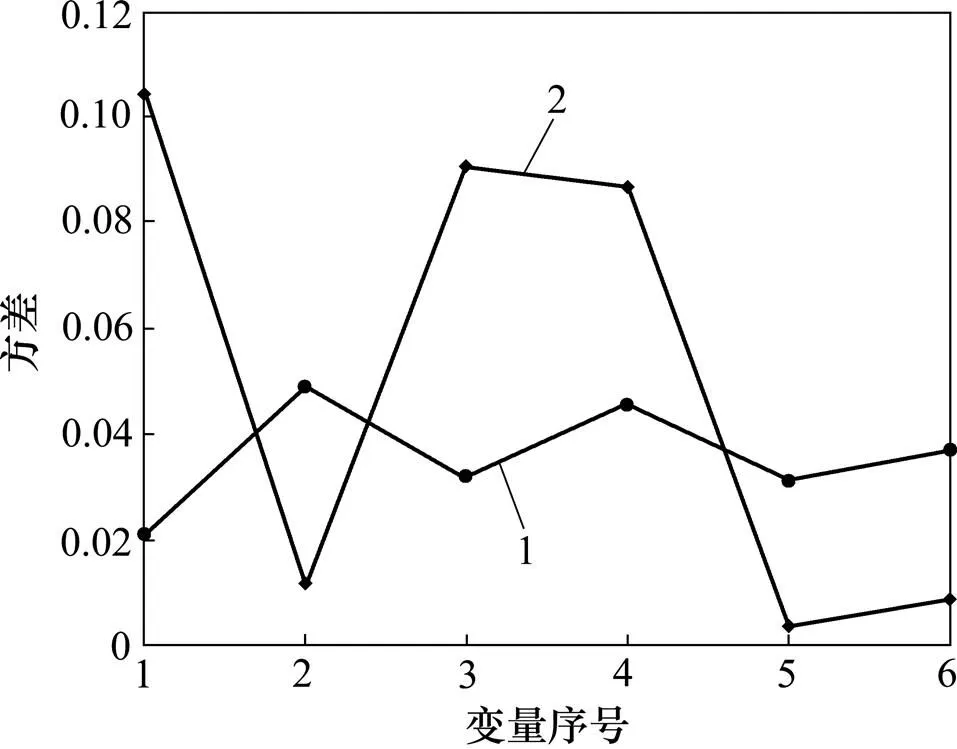
1—训练集统计量；2—测试集统计量。

3.2 TE过程仿真

TE过程是由伊斯曼化学品公司创建的，其目的是为评价过程控制和监控方法提供一个现实的工业过程。测试过程是基于一个真实工业过程的仿真，包含41个测量变量和12个控制变量。过程仿真包括21个预设定的故障，其中16个是已知的，5个是未知的，详细介绍见文献[19−20]。在本文中，最后一个控制变量在过程中基本不会发生变化。因此建立模型时采用41个测量变量以及11个控制变量，共52个变量[21]。TE过程收集训练数据采样周期为24 h，采样间隔为3 min。测试数据的采样周期为48 h，前8 h为正常数据，后面引入故障。因此，用来建模的数据训练集维数为480×52，测试集维数为960×52，第161个数据点引入的故障。参数根据公式以及经验选取。在本次实验中，选择，得到的实验结果如图5~8所示。图5~8中所示的是在TE过程中比较有代表性的2个故障：故障1和故障5。

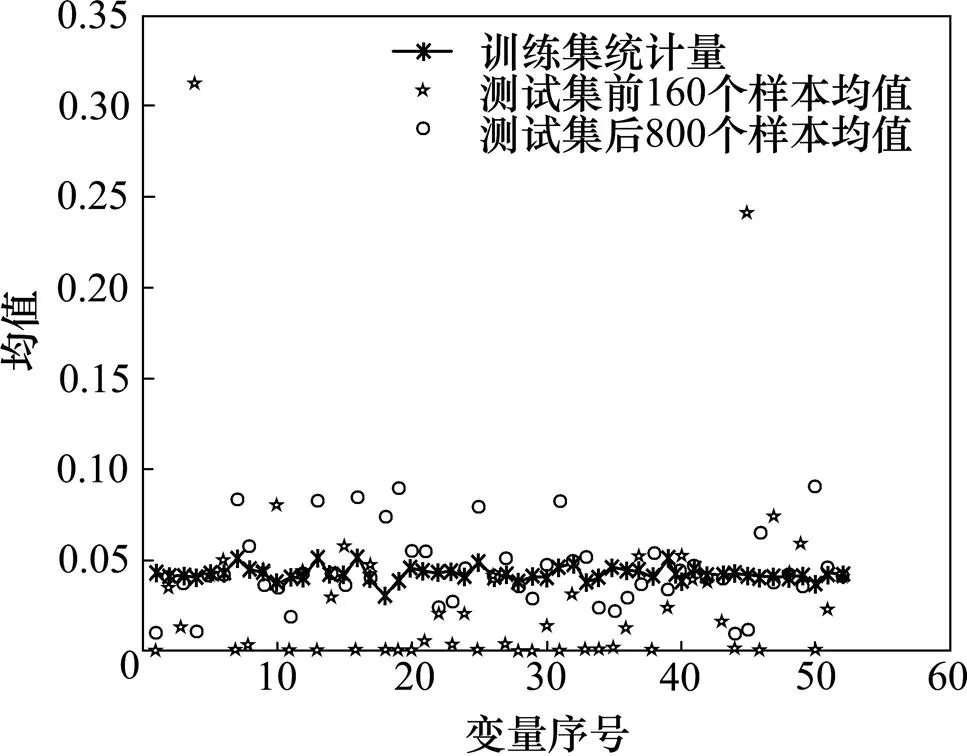
图5 TE过程故障1发生时52个变量均值分布

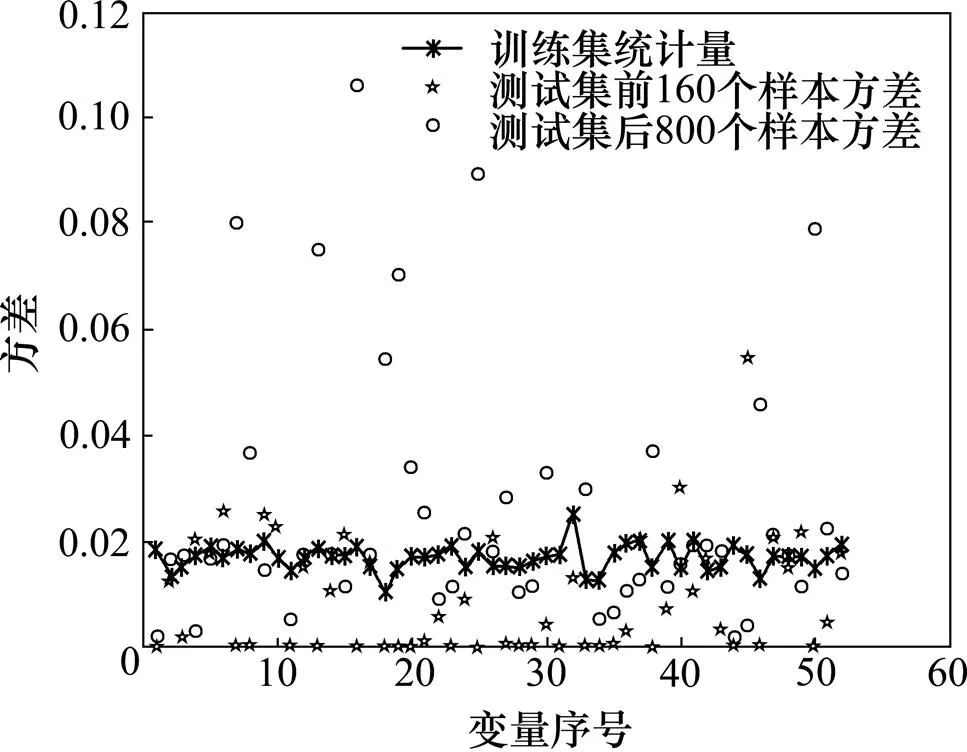
图6 TE过程故障1发生时52个变量的方差分布图

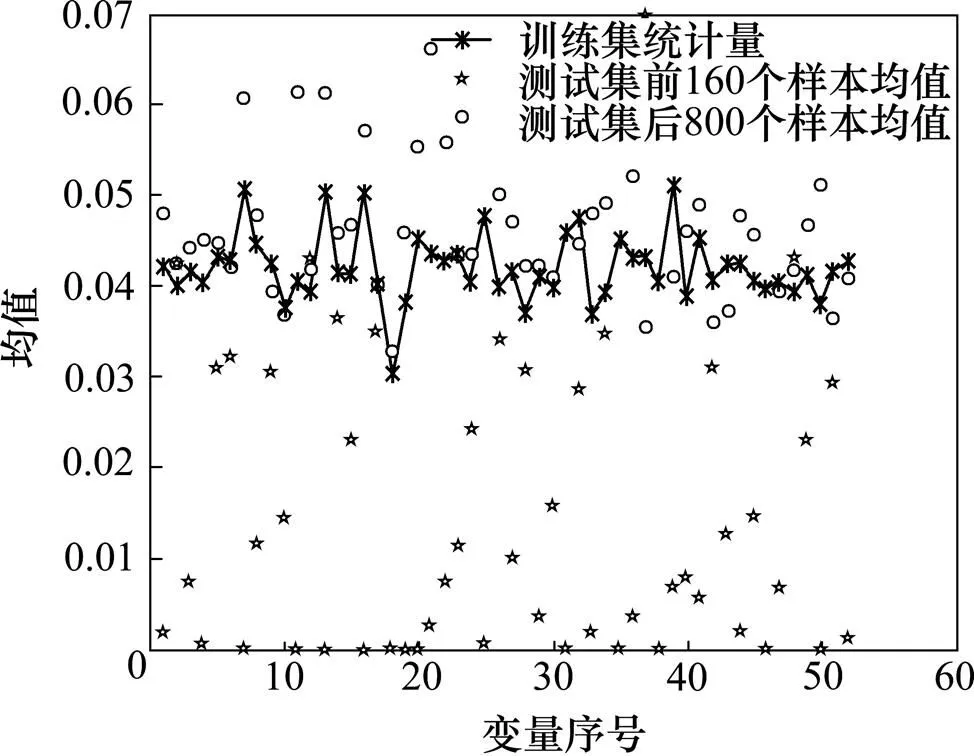
图7 TE过程故障5发生时52个变量的均值分布

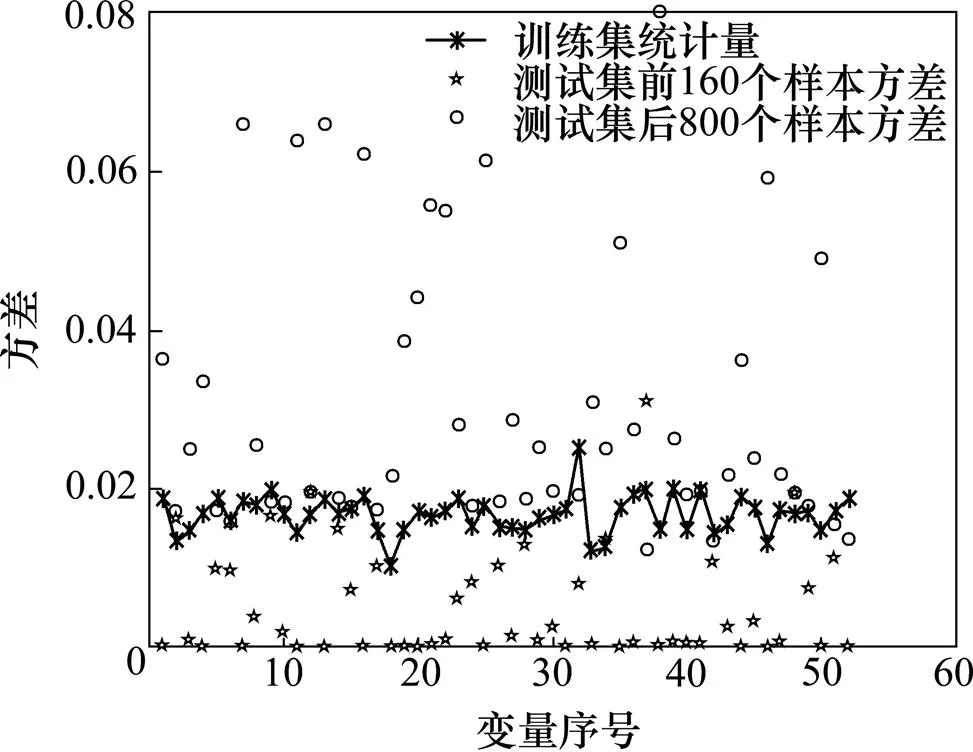
图8 TE过程故障5发生时52个变量的方差分布

从图5~8可以看出：测试集后800个样本均值或方差比训练集统计量的大，而测试集前160个样本均值或方差与训练集统计量的相近或略小，因此，使用这种统计量能够进行过程监测。当观察到超出正常阈值的‘○’点时，可以识别出发生故障的变量，此时低秩矩阵为过程重构矩阵。但因为TE过程有52个变量，而且每个故障出现和不同的变量相关，在故障发生的时候也不一定是全部的变量都超出正常的阈值。因此，在本故障检测中，若某个过程后800个样本点变量的均值方差超过训练集变量的均值方差的个数多于前160个正常样本点变量的均值方差超过训练集变量的均值方差的个数，均值和方差这2个统计量中任何一个超过阈值时则判断发生故障。在TE过程中，利用均值方差统计量能够实现过程监测的4个步骤，这种统计量是可行的。但是在实际的工业生产中，不会存在像TE过程前160个正常样本点这样的数据，所以为了判断某个过程是否出现故障，可以利用前一段时间正常运行非训练集中的数据来代替TE过程中的前160个正常样本点。同样还是比较正常数据超过阈值的变量数和测试数据超过阈值的变量数。

4 结论

1) 利用PCP进行矩阵分解得到的低秩矩阵不包含噪声和故障，它们被放在稀疏矩阵中。因此，PCP方法对过程监测是适用的。

2) 针对使用PCP方法的特点，提出了一种利用均值方差统计指标来构建的统计量。并且在数值仿真和TE过程上面进行仿真，效果良好。

3) 由于PCP算法是一个矩阵分解方法，所以，本文提出的均值和方差统计量方法不能实现在线实时监测，还需要改进统计量。

[1] 葛志强. 复杂工况过程统计监测方法研究[D]. 杭州: 浙江大学控制科学与工程学院, 2009: 5−12. GE Zhiqiang. Statistical process monitoring methods for complex processes[D]. Hangzhou: Zhejiang University. Department of Control Science and Engineering, 2009: 5−12.

[2] 周东华, 胡艳艳. 动态系统的故障诊断技术[J]. 自动化学报, 2009 (6): 748−758. ZHOU Donghua, HU Yanyan. Fault diagnosis techniques for dynamic systems[J]. Acta Automatica Sinica, 2009 (6): 748−758.

[3] QIN S J. Survey on data-driven industrial process monitoring and diagnosis[J]. Annual Reviews in Control, 2012, 36(2): 220−234.

[4] GE Zhiqiang, SONG Zhihuan, GAO Furong. Review of recent research on data-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543−3562.

[5] WANG Youqing, FAN Jicong, YAO Yuan. Online monitoring of multivariate processes using higher-order cumulants analysis[J]. Industrial & Engineering Chemistry Research, 2014, 53(11): 4328−4338.

[6] CANDÈS E J, LI X, MA Y. Robust principal component analysis[J]. Journal of the ACM (JACM), 2011, 58(3): 11.

[7] CHANDRASEKARAN V, SANGHAVI S, PARRILO P A, et al. Rank-sparsity incoherence for matrix decomposition[J]. SIAM Journal on Optimization, 2011, 21(2): 572−596.

[8] ZHOU Z, LI X, WRIGHT J, et al. Stable principal component pursuit[C]// 2010 IEEE International Symposium on Information Theory Proceedings (ISIT). Austin: IEEE, 2010: 1518−1522.

[9] XU H, CARAMANIS C, SANGHAVI S. Robust PCA via outlier pursuit[C]// Advances in Neural Information Processing Systems. Vancouver, 2010: 2496−2504.

[10] CANDÈS E J, RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717−772.

[11] CHANDRASEKARAN V, SANGHAVI S, PARRILO P, et al. Sparse and low-rank matrix decompositions[C]// 47th Annual Allerton Conference on Communication, Control, and Computing. Monticello: IEEE, 2009: 962−967.

[12] BOUWMANS T, ZAHZAH E H. Robust PCA via principal component pursuit: a review for a comparative evaluation in video surveillance[J]. Computer Vision and Image Understanding, 2014, 122: 22−34.

[13] ISOM J D, LABARRE R E. Process fault detection, isolation, and reconstruction by principal component pursuit[C]// American Control Conference. San Francisco, USA: IEEE, 2011: 238−243.

[14] CHENG Yue, CHEN Tongwen. Application of principal component pursuit to process fault detection and diagnosis[C]// American Control Conference. Washington, USA: IEEE, 2013: 3535−3540.

[15] CHEN Dan, LI Zetao, HE Zhiqin. Research on fault detection of tennessee eastman process based on PCA[C]// 25th Control and Decision Conference (CCDC). Guiyang, 2013: 1078−1081.

[16] CAI J F, CANDÈS E J, SHEN Z. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956−1982.

[17] XIE Lei, LIN Xiaozhong, ZENG Jiusun. Shrinking principal component analysis for enhanced process monitoring and fault isolation[J]. Industrial & Engineering Chemistry Research, 2013, 52(49): 17475−17486.

[18] ALCALA C F, QIN S J. Reconstruction-based contribution for process monitoring[J]. Automatica, 2009, 45(7): 1593−1600.

[19] CHIANG L H, RUSSELL E L, BRAATZ R D. Fault diagnosis in chemical processes using Fisher discriminant analysis, discriminant partial least squares, and principal component analysis[J]. Chemometrics and Intelligent Laboratory systems, 2000, 50(2): 243−252.

[20] CHIANG L H, BRAATZ R D, RUSSELL E L. 工业系统的故障检测与诊断[M]. 段建民, 译. 北京: 机械工业出版社, 2003: 125−160. CHIANG L H, BRAATZ R D, RUSSELL E L. Fault detection and diagnosis in industrial systems[M]. DUAN Jianmin, trans. Beijing: China Machina Press, 2003: 125−160.

[21] YIN S, DING S X, HAGHANI A, et al. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process[J]. Journal of Process Control, 2012, 22(9): 1567−1581.

(编辑 杨幼平)

Process monitoring based on principal component pursuit

PAN Yijun, YANG Chunjie, SUN Youxian, ZHOU Zhe, AN Ruqiao

(School of department of Control Science and Engineering, Zhejiang University，Hangzhou 310027, China)

To apply principal component pursuit (PCP) method for process monitoring, a mean variance statistic was proposed for process monitoring. First, the standardized training and testing data matrices were decomposed by PCP. Then the mean and variance of each variable were calculated in corresponding sparse matrix. The numerical simulation and TE process were provided. The results show that this statistic can eliminate the influence of almost noise interference in process. It can accomplish the objectives of model building, fault detection, fault isolation, and process reconstruction simultaneously, and illustrate the effectiveness of proposed statistic.

process monitoring; principal component pursuit; TE process; mean variance

10.11817/j.issn.1672-7207.2017.01.018

TP277

A

1672−7207(2017)01−0127−07

2016−01−10；

2016−03−15

国家高技术研究发展计划(863计划)项目(2012AA041709)；国家自然科学基金资助项目(61290321) (Project(2012AA041709) supported by the National High Technology Research and Development Program (863 Program) of China; Project(61290321) supported by the National Natural Science Foundation of China)

杨春节，博士，教授，从事工业过程建模、过程监测、高炉故障诊断研究；E-mail: cjyang@iipc.zju.edu.cn