牵引策略对动车组运行能耗的影响

喻李葵，沈杰，苏博，马卫武，李立清



牵引策略对动车组运行能耗的影响

喻李葵，沈杰，苏博，马卫武，李立清

(中南大学能源科学与工程学院，湖南长沙，410083)

通过理想化假设，分析曲线、坡道、桥梁、隧道对动车组受力的影响，建立动车组牵引能耗仿真计算模型，并根据实际线路运行结果对模型进行验证。在实际线路参数的基础上，通过能耗模型模拟计算研究启动加速阶段、中间运行阶段以及制动阶段的不同牵引策略对动车组的运行时间、能耗的影响，并提出评价动车组牵引能耗的时间−牵引能耗经济性指标，以考察各种牵引策略的节能、节时潜力。研究结果表明：在惰行终点速度为110 km/h时，动车组牵引能耗达到1个能耗局部最低点。

牵引策略；仿真模型；运行能耗；经济性指标

随着我国铁路的迅速发展，动车组客运量不断增加，动车组的节能问题日益突出。优化牵引策略是列车节能操纵、控制优化的重要途径，能够有效降低动车组运行的能耗水平。一些研究者定性地给出了优化牵引策略的方法。对于短途轨道交通来说，MILROY[1]提出最节能的牵引策略应为“最大启动加速运行—匀速运行—最大减速制动”3个阶段，实验证明这是正确的[2]。在此基础上，针对长途轨道交通，JIAXIN 等[3]认为最优牵引策略应该包括“最大启动加速运行—匀速运行—惰行—减速制动”4个过程。基于最大值原理，KHMELNITSKY等[4]采用数值计算方法求出不同操纵策略下列车牵引和制动的最小能耗。HOWLETT等[5]用局部最小值原理计算大梯度下全局最优策略的临界点并通过把最优转换点反馈给驾驶员，提供驾驶意见。LIU等[6]用一种分析程序确定列车的最优操纵从而确定最小耗能，并且给出了连续的最优控制方程从而找到了控制变化点。BOCHARNIKOV等[7]通过变量权重设计了1个适度函数以找到列车节约能量和更快运行的平衡点，通过运行一系列类似于遗传算法的仿真程序来确定最优牵引策略。张星臣等[8−12]对影响列车牵引能耗的各因素进行了模拟研究，重点分析了线路属性因素的影响以及制动利用率对节能操纵率的影响。荀径等[13−14]对节能操纵优化解法进行了综述，分析了解析方法、数值方法和仿真方法的研究现状与投入应用的情况，并对列车紧急制动距离限值核定的原则进行了探讨。在牵引仿真领域，康熊等[15−19]提出了包含能耗、运行时分和停站精度在内的多目标列车运行仿真模型，对高速铁路使用阶段碳排放量进行核算，并运用基于Web的智能客户端体系结构，开发了列车牵引分析计算系 统，同时对铁路智能运输系统及其应用进行了分析。本文作者结合实验调研所得线路参数，通过对动车组运行过程多因素进行分析，建立动车组牵引能耗仿真模型，研究给定线路条件下不同牵引策略对动车组牵引能耗的影响，并提出动车组牵引能耗评价指标，以评价牵引策略的时间经济性。

1 动车组运行能耗模型与仿真

1.1 动车组运行过程分析

在牵引阶段，当坡道为下坡且坡道阻力大于其他阻力之和时，列车在惰行状态下作加速运动，若达到最大速度max，则需进行制动。为避免这种情况，设列车以惰行工况运行至坡道终点时，达到最大速度max，根据受力情况即可得到列车不进行下坡制动时列车运行速度与路程之间的关系曲线。在列车运行过程中，一旦列车运行曲线与该曲线相交，即转为惰行工况。为避免因桥梁限速使列车进入制动工况增加能耗，根据加算坡道附加阻力得到列车惰行至桥梁起点的惰行曲线。在列车运行过程中，一旦列车运行曲线与惰行曲线相交，即转为惰行工况。

在制动阶段，制动力可以通过制动特性曲线查得，在列车总质量和线路条件已知的条件下，根据牛顿运动学公式可知：

(2)

(3)

式中：为回转质量系数，即回转折合质量与动车组总质量之比，取值0.11[20]；为重力加速度，取值9.8 m/s2；为单位重力所受合力，N/kN；0为单位重力动车组所受基本阻力，N/kN；j为单位重力动车组所受加算坡道附加阻力，N/kN。制动结束时，2为0 km/h，即列车静止，这样就得到列车进站制动时的列车制动−曲线。在列车运行过程中，一旦列车运行曲线与制动−曲线相交，即转为制动工况。

1.2 动车组牵引能耗计算基础

根据能耗计算方法同时结合能量转换理论，推导改进牵规后的计算能耗算法如下：

(5)

其中：为牵引能耗，kW·h；0为制动能耗，kW·h；1为合力能耗，kW·h；2为基本阻力能耗，kW·h；3为附加阻力能耗，kW·h。根据做功公式和功能转换原理，可推得动车组所受合力能耗1：

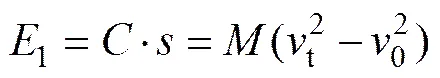
同时有：

(7)

其中：为距离，km；为列车质量，t;t为末速度，km/h；0为初速度，km/h；，和为列车类型相关系数；i，s和r分别为坡道、隧道、曲线附加阻力，N/kN。在运动过程中，加速段和减速段取平均阻力取平均阻力，则基本阻力能耗公式可变为

(9)

在得到动车组机组数据和运行路线参数后，先通过上述方法对线路参数进行预处理，得到限速处惰行曲线和机车进站制动曲线，再根据列车能耗计算方法对列车运行能耗进行计算，得到列车运行能耗。以启动牵引过程为例，该仿真的计算流程见图1。

图1 牵引过程仿真计算流程

2 动车组牵引策略优化

2.1 动车组能耗的线路参数调研选取

线路曲线、坡道、桥梁、隧道等因素会影响列车的运行能耗和时间，现选取这4个因素的调研数据加以分析。长吉(长春—吉林)城际铁路坡度、曲率半径、桥梁、隧道参数见表1~4。

表1 长吉城际铁路坡度参数

表2 长吉城际铁路曲率半径参数

表3 长吉城际铁路桥梁参数

表4 长吉城际铁路隧道参数

2.2 动车组能耗仿真模型的验证分析

为验证上述仿真模型正确性，对D5037次长春—吉林动车组的运行进行模拟计算，将调研得到的运行结果与计算所得结果进行对比，如图2及表5所示。

由图2和表5可知：在运行过程中，牵扯引能耗计算结果能较好地符合调研结果，相对误差为2.9%，在误差允许范围以内。

2.3 不同阶段不同牵引策略对动车组的运行时间和能耗的影响

2.3.1 启动阶段

为研究启动阶段牵引策略对动车组能耗、时间的影响，以长吉线为例，对动车组的运行进行模拟，分60%，80%和100% 3种牵引工况进行牵引，中间运行阶段均采用200 km/h匀速牵引，制动阶段采用最大制动力制动。得到不同牵引启动过程的计算结果如表6所示。

1—调研结果；2—计算结果。

不同牵引启动工况启动阶段−曲线如图3所示。

启动工况：1—100%；2—80%；3—60%。

从表6可知：动车组采用不同启动工况牵引加速，3种牵引工况下动车组在牵引运行和制动阶段产生的能耗、所需时间均基本相同。动车组在不同牵引工况下总体牵引能耗、运行时间的差别主要由于启动工况不同而产生。

在一般情况下，采用不同牵引工况启动加速时，动车组从速度为0 km/h加速至最大速度，100%牵引工况所需时间应为最小且所需加速路程也最小，从而以该工况启动加速会造成动车组在牵引运行阶段所需路程较长。因此，以较大牵引工况启动时，动车组在中间牵引阶段牵引能耗和运行时间会比以较小牵引工况启动时更大。

而在计算过程中，可以发现在不同牵引工况启动加速时，动车组从速度为0 km/h加速至最高速度，3种牵引工况所需时间和所需加速路程差别不大。由图3可知：在80%和60%启动牵引工况下，动车组在距起点13.2 km附近在很短路程内加速至最大速度，使其与100%启动牵引工况用相同路程达到最大速度。造成这一现象的原因是距起点13.1~14.5 km处，存在1个坡度为7.5‰的下坡路段，即动车组在此路段所受坡道的附加阻力起促进作用，造成动车组在此路段以较大加速度完成加速。

表5 能耗计算值及分析结果

表6 不同启动工况下动车组运行时间和能耗

Table 6 Time and energy consumption under different start states

采用启动牵引策略时，应结合线路具体线路情况，考虑动车组安全、快速要求，在节能的基础上进行选择。

2.3.2 中间牵引运行过程

惰行可以有效降低列车能耗，通过选择合适的惰行点可以实现列车的节能运行。为研究中间牵引运行过程的牵引策略对动车组运行能耗的影响，选取100%牵引工况启动加速，中间牵引过程采用惰行−牵引反复进行的策略，分别取惰行终点速度为180，90和0 km/h，制动阶段采用最大制动力制动。得到不同中间牵引过程模拟结果如表7所示。不同中间牵引过程−曲线如图4所示。

惰行终点速度/(km·h−1)：1—180；2—90；3—0。

从表7可知：惰行终点速度为180，90和0 km/h时，牵引能耗与匀速牵引策略相比分别少12.5%，46.7%和70.3%，总能耗分别减少10.3%，36.7%和53.3%，相应运行时间比采用匀速牵引策略分别增加2.8%，24.3%和72.4%。可见：惰行终点速度越小，能耗越小，但时间会增加；在时间允许的情况下，应尽量进行惰性牵引。

由图4可知：在惰行过程中，速度会有增加的区域，这是由于存在下坡道。合理利用线路条件对于节能省时是有利的。

2.3.3 制动阶段

不同中间牵引运行策略制动阶段−曲线如图5所示。在计算中发现，长吉城际铁路在接近终点处，有较大坡度且较长的下坡路段，造成动车组不可能以惰行至终点。由图5可知：在惰行终点速度为130 km/h的工况下，运行曲线与制动曲线在速度为172 km/h处相遇；而当惰行终点速度为140 km/h时，运行曲线与制动曲线在速度为160 km/h处相遇。

惰行终点速度/(km·h−1)：1—130；2—140。

由表8可知：在中间惰行终点速度为140 km/h时，所用牵引能耗反而比中间惰行速度为130 km/h时的小。在计算过程中发现：两者在启动阶段和中间牵引阶段产生的牵引能耗相差很少，只是由于在制动阶段产生的制动能耗差距较大，造成2种工况下总牵引能耗存在差距。

表7 100%启动下不同惰行终点速度时的模拟结果

表8 100%启动下不同中间过程工况的模拟结果

因此，在动车组牵引过程中，应尽量惰行至较小速度进入制动过程，以减少动能损失，降低制动能耗，从而降低运行过程的牵引能耗和总能耗。

2.4 不同牵引策略的时间−能耗经济性评价指标

为更进一步验证上述规律并找到最佳牵引策略，取更多不同惰行终点速度进行计算，计算结果如图6所示。

1—运行总牵引能耗；2—运行总时间。

图6大体反映了惰行终点速度越小，动车组牵引能耗越小而运行时间越长的规律。在制定动车组牵引策略时，应在满足区段对运行时间的要求下，尽量降低惰行终点速度，以尽量减少动车组运行能耗。

从图6可知：在惰行终点速度为110 km/h时，动车组牵引能耗达到1个能耗局部最低点。将该点定义为临界惰行终点速度，超过临界速度后，随着惰行终点速度降低反而能耗增大。这是由于当惰行终点速度小于临界值时，进一步减小惰行终点速度，惰行能力降低，惰行过程减少，能耗幅度减小；同时，由于牵引初速度较小，增大了动车组牵引难度，使中间牵引过程的能耗量大于由于惰行终点速度降低而减少的能耗。所以，在制定牵引策略时，应尽量使惰行终点速度大于临界惰行终点速度。

在不同牵引策略下，动车组运行时间越长，牵引能耗越小，总能耗越小。若从减少能源消耗的方面考虑，则运行时间越长越好，而这与动车组高效、省时的要求不符。因此，在确定动车组牵引策略时，需要找到动车组节能和节时之间的平衡点。为明确两者之间的关系，并为制定动车组牵引策略提供参考，提出给定线路的时间−牵引能耗经济性指标：

其中：为采用任一牵引策略动车组的牵引能耗，kW·h；min为采用不同牵引策略时动车组最小牵引能耗；max为采用不同牵引策略时动车组最大牵引能耗；为采用任一牵引策略动车组运行时间，min；min为采用不同策略时动车组最小运行时间，min；max为采用不同策略时动车组最大运行时间，min。

对牵引启动阶段采用100%启动的牵引策略，分别计算不同惰行终点速度下的，计算结果如表9所示。

由表9可知：随惰行终点速度降低而降低，即动车组继续降低惰行终点速度，在节省相同牵引能耗的条件下，所增加的运行时间随之增加。在惰性终点速度为110 km/h时，有1个局部最小值，表明在该惰性速度下，动车组的时间−牵引能耗经济性较好。对比惰性速度为50 km/h与40 km/h时发现在该速度间隔中，发生了较大变化。图7所示为与预测的惰性终点速度的关系。从图7可知：当惰性速度由50 km/h变为40 km/h时，动车组运行能耗和运行时间均出现大幅度变化。

当0≤＜200 km/h时，对惰行终点速度和相应进行拟合，得到以下规律：

式中：为惰行终点速度，km/h。

与惰行终点速度中拟合曲线的可决系数为0.928 2，误差方差2为265.9，拟合度较高。可以通过上述关系由惰行终点速度估计，以确定最优牵引策略。

表9 不同牵引策略下的T

图7 T与预测的惰行终点速度的关系

3 结论

1) 以较大牵引工况启动时，动车组在中间牵引阶段牵引能耗和运行时间会比以较小牵引工况启动时更大。受下坡道的影响，牵引能耗和运行时间计算结果有所差别。采用何种启动牵引策略，应再结合线路具体线路情况，考虑动车组安全、快速要求，在节能的基础上进行选择。

2) 在模拟线路中，当惰行终点速度为110 km/h时，动车组牵引能耗达到1个能耗局部最低点。在动车组运行的中间牵引过程，采用牵引−惰行策略运行可明显降低动车组能耗，延长动车组运行时间，且惰行终点速度越低，这种影响效果越明显。

3) 在动车组运行的制动阶段，由于吉林—长春段不能采用惰行到终点的策略，因此，采用何种制动工况需结合线路条件考虑。在采用惰行−制动策略进行制动时，应尽量使动车组以较小速度进入制动阶段，以减小动车组动能消耗及制动能耗。

4) 为明确动车组不同牵引策略下动车组运行时间与能耗的关系，研究不同中间惰行速度下的节能、节时潜力，提出牵引能耗的时间−牵引能耗经济性指标，以考察动车组不同牵引策略的节能、节时潜力。

[1] MILROY I P. Minimum-energy control of rail vehicles[M]. Adelaide, Australian: South Australian Institute of Technology, 1981: 103.

[2] BENJAMIN B R, LONG A M, MILROY I P, et al. Control of railway vehicles for energy conservation and improved timekeeping[C]// Conference on Railway Engineering. Perth, Australia: Institution of Engineers, 1987: 41−47.

[3] JIAXIN C, HOWLETT P G. A note on the calculation of optimal strategies for the minimization of fuel consumption in the control of trains[J]. IEEE Transactions on Automatic Control, 1993, 38(11): 1730−1734.

[4] KHMELNITSKY E. On an optimal control problem of train operation[J]. IEEE Transactions on Automatic Control, 2000, 45(7): 1257−1266.

[5] HOWLETT P G, PUDNEY P J, VU X. Local energy minimization in optimal train control[J]. Automatica, 2009, 45(11): 2692−2698.

[6] LIU R R, GOLOVITCHER I M. Energy-efficient operation of rail vehicles[J]. Transportation Research Part A: Policy and Practice, 2003, 37(10): 917−932.

[7] BOCHARNIKOV Y V, TOBIAS A M, ROBERTS C, et al. Optimal driving strategy for traction energy saving on DC suburban railways[J]. IET, Electric Power Applications, 2007, 1(5): 675−682.

[8] 张星臣, 冯雪松, 毛保华, 等. 我国高铁列车牵引能耗影响因素作用效果的模拟分析[J]. 交通运输系统工程与信息, 2011, 11(3): 83−86. ZHANG Xingchen, FENG Xuesong, MAO Baohua, et al. Simulation research on the traction energy consumption of high-speed trains in China[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(3): 83−86.

[9] 冯佳, 许奇, 冯旭杰, 等. 基于灰色关联度的轨道交通能耗影响因素分析[J]. 交通运输系统工程与信息, 2011, 11(1): 142−146. FENG Jia, XU Qi, FENG Xujie, et al. Influencing factors of energy consumption for rail transport based on grey relational degree[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(1): 142−146.

[10] 陈涛. 高速列车运行能耗测算方法及其影响因素量化分析[D]. 北京: 北京交通大学交通运输学院, 2011: 1−30. CHEN Tao. Traction energy consumption measuring methods study and quantification analysis on energy impact factors of high-speed train[D]. Beijing: Beijing Jiaotong University. School of Traffic and Transportation. 2011: 1−30.

[11] 薛艳冰, 马大炜, 王烈. 列车牵引能耗计算方法[J]. 中国铁道科学, 2007, 28(3): 84−87. XUE Yanbing, MA Dawei, WANG Lie. Calculation method of energy consumption in train traction[J]. China Railway Science, 2007, 28(3): 84−87.

[12] 崔恒斌, 冯晓云, 王青元, 等. 制动利用率对高速列车节能操纵策略的影响[J]. 铁道学报, 2012, 34(8): 13−19. CUI Hengbin, FENG Xiaoyun, WANG Qingyuan, et al. Influence of braking efficiency on high-speed train energy-saving driving strategies[J]. Journal of the China Railway Society, 2012, 34(8): 13−19.

[13] 荀径, 杨欣, 宁滨, 等. 列车节能操纵优化求解方法综述[J]. 铁道学报, 2014, 36(4): 14−20. XUN Jing, YANG Xin, NING Bin, et al. Survey on trajectory optimization for train operation[J]. Journal of the China Railway Society, 2014, 36(4): 14−20.

[14] 黄问盈, 杨宁清, 黄民. 我国铁道列车紧急制动距离限值核定原则的探讨[J]. 中国铁道科学, 2003, 24(3): 79−88. HUANG Wenying, YANG Ningqing, HUANG Min. Study on verification principle of emergency brake distance limit of Chinese Railway Train[J]. China Railway Science, 2003, 24(3): 79−88.

[15] 康熊.高速动车组列车牵引仿真计算技术研究[J]. 中国工程科学, 2011, 13(1): 62−68. KANG Xiong. Study on train traction simulation of high speed motor train set[J]. Engineering Sciences, 2011, 13(1): 62−68.

[16] 石红国, 彭其渊.列车运行过程仿真及优化研究[D]. 成都: 西南交通大学交通运输与物流学院, 2006: 1−70. SHI Hongguo, PENG Qiyuan. Study on train operation and movement process simulation and its’ optimization[D]. Chengdu: Southwest Jiaotong University. School of Transportation and Logistics, 2006: 1−70.

[17] 宋晓东, 付延冰, 刘恒斌, 等. 基于生命周期评价的高速铁路减排效果[J].中南大学学报(自然科学版), 2014, 45(9): 3301−3307. SONG Xiaodong, FU Yanbing, LIU Hengbin, et al. Carbon dioxide emission reduction of high-speed railway[J]. Journal of Central South University (Science and Technology), 2014, 45(9): 3301−3307.

[18] 童林军.基于WEB的列车牵引计算研究与软件开发[D]. 长沙: 中南大学交通运输工程学院, 2008: 1−80. TONG Linjun. Developed web-based software system for the train traction calculation[D]. Changsha: Central South University. Traffic and Transportation Engineering, 2008: 1−80.

[19] 贾利民, 秦勇, 张媛. 铁路智能运输系统及其应用[J]. 中南大学学报(自然科学版), 2011, 42(1): 1042−1047. JIA Limin, QIN Yong, ZHANG Yuan. Railway intelligent transportation system and its application[J].Journal of Central South University (Science and Technology), 2011, 42(1): 1042−1047.

[20] 宋锴, 牛会想.回转质量系数对高速列车牵引电算的影响[J]. 铁道机车车辆, 2010, 30(3): 56−59. SONG Kai, NIU Huixiang. Influence of rotary mass coefficient in high speed train traction calculation[J].Railway Locomotive & Car, 2010, 30(3): 56−59.

(编辑 陈灿华)

Impact of traction strategy on traction energy consumption of CRH

YU Likui, SHEN Jie, SU Bo, MA Weiwu, LI Liqing

(School of Energy Science and Engineering, Central South University, Changsha 410083, China)

The effect of curve, ramp, bridge and tunnel on the force of CRH was analyzed to establish a calculation model of traction energy consumption of CRH, which was verified by field results. The calculation model was used to study the effect of traction strategy on traction energy consumption and running time of the CRH in different operation stages. In order to evaluate the energy-saving and time-saving potential of different traction strategies, the traction energy consumption time-economy index was put forward. The results show that the traction energy consumption of the CRH is the lowest when the coasting speed is 110 km/h.

traction strategy; simulation model; energy consumption; time-economy index

10.11817/j.issn.1672-7207.2017.01.035

U266.2

A

1672−7207(2017)01−0262−08

2016−01−10；

2016−03−15

铁道部科技研究开发重点项目(2012Z001-B)；国家科技支撑计划项目(2015BAL04B02)；中南大学中央高校基本科研业务费专项资金资助项目(2014zzts194) (Project(2012Z001-B) supported by the Major Science and Technology Foundation of Ministry of Railway of China; Project(2015BAL04B02) supported by the National Key Technology R&D Program of China; Project(2014zzts194) supported by the Fundamental Research Funds for the Central Universities)

马卫武，博士，副教授，从事铁路节能减排研究；E-mail: maweiwu@csu.edu.cn