烧结矿余热回收竖罐内气体的流动特性
冯军胜,董辉,李含竹,高建业
烧结矿余热回收竖罐内气体的流动特性
冯军胜,董辉,李含竹,高建业
(东北大学冶金学院,国家环境保护生态工业重点实验室,辽宁沈阳,110819)
采用对Ergun型方程量纲一化的方法对气体通过烧结矿床层的压力降和流态进行研究,考察气体表观流速和烧结矿颗粒直径对床层内压力降及流态的影响。研究结果表明:当颗粒直径一定时,床层内单位料层高压力降随气体表观流速的增大呈二次方关系增大。当气体表观流速一定时,单位料层高压力降随颗粒直径的增大呈指数关系衰减。提出床层内临界颗粒雷诺数随颗粒当量直径变化的实验预测关联式,相对误差在±5%以内。提出床层内Forchheimer流区和湍流区的压力降实验预测关联式,相对误差均在±8%以内,显示良好的预测性能。
烧结;填充床;压力降;流态;临界雷诺数
烧结过程余热资源高效回收与利用是降低烧结工序能耗的主要途径之一[1]。烧结矿余热竖罐式回收是针对于传统烧结余热回收系统的弊端[2],借鉴干熄焦炉的结构和工艺提出的一种烧结矿显热高效回收方式[3−6]。就结构特点而言,烧结矿余热回收罐体属于大颗粒随机填充床范畴,竖罐内烧结矿的填充结构近似于多孔介质,罐体内气体通过烧结料层的流动特性是决定烧结余热罐式回收可行性的关键问题。近年来,已有不少学者对流体通过多孔介质的流动特性进行了研究。1856年提出的Darcy关系式描述了多孔介质内单相流速与压力降之间的关系,但此关系式只适合低雷诺数下的流体流动[7]。FORCHHEIMER指出多孔介质中单相流的压力降实际上由黏性力和惯性力2部分组成,并提出了适合求解高雷诺数下多孔介质内流体压力降的非线性方程[8]。随后,许多学者在Forchheimer 研究的基础上,采用球体颗粒或均匀颗粒填充构成的多孔介质骨架,以水或者空气作为介质,进行了多孔介质通道阻力特性的研究,并且拟合出了不同多孔介质单相流体流动阻力的预测模型[9−14],其中以Ergun的研究最具有代表性。ERGUN等[9−10]认为高雷诺数下多孔介质中单相流的压力降为流体表观速度的一次项和二次项之和,提出了著名的Ergun关系式。在Ergun关系式应用的过程中,多位研究人员又对Ergun关系式中的系数提出修正,使其适用于不同的颗粒填充 床[15−18]。随着数值模拟研究在多孔介质内流动和传热过程中的不断深入,流动模型的选择显得尤为重要,因而多孔介质内流体流态的分区也被多位学者所研究。RODE等[19−20]采用电化学探针的技术方法对不同孔隙结构的多孔介质的流态转变进行了大量实验研究。实验主要目的是为了确定不同孔隙结构的多孔介质层流区间的具体划分点,同时考虑了颗粒直径和孔隙率的变化等因素对流态区间划分的影响。FAND 等[21]通过对Ergun型方程进行量纲一化,同时根据床层内量纲一压力降随雷诺数的变化趋势的不同,得到了流态的分区,认为流体通过多孔介质时流态大致可分为:前达西流区、达西流区、Forchheimer流区和湍流区。KECECIOGLU等[22]在FAND等[21]研究的基础上提出了对Ergun型方程量纲一化的新方法,给出了与FAND等[21]研究结果基本一致的流态划分区间。但迄今为止,对多孔介质内流体流动特性的研究还主要集中于球体或者均匀颗粒的填充床内,而关于烧结矿这种形状不均的大颗粒填充床内流体流动特性的研究还鲜有报道,也就是并没有考虑非均匀颗粒的形状因子对填充床内流体流动特性的影响。基于此,本文作者在自制气固流动实验装置的基础上,采用对表征烧结矿床内气体流动特性的Ergun型方程进行量纲一化的方法,研究了气体表观流速和烧结矿颗粒直径对床内气体压力降和流态的影响,并在此基础上,拟合出了不同流态区域描述床层阻力特性的Ergun修正关联式,旨在为烧结矿余热竖罐的设计和优化提供理论 依据。
1 实验方法及装置
1.1 实验方法
由文献[9−10]可知,求解颗粒填充床内流体压力降的Ergun公式如下:

文献[16−18]中所提出的Ergun型关系式只是对原有Ergun公式中表观速度的一次项和二次项系数进行修正,使其求解不同多孔介质空隙结构内流体的压力降。由此可得求解颗粒填充床内流体压力降的普适Ergun型方程为
(2)
考虑到烧结矿为非均匀颗粒,将颗粒形状因子对流体压力降的影响引入到式(2)中,可得到如下非均匀颗粒填充床内的Ergun型方程。

根据文献[21−22]提出的方法,对式(3)进行量纲一化,可得如下关系式。
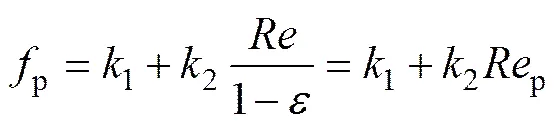
其中:
(5)

(7)
式中:p为颗粒摩擦因子;为颗粒表观雷诺数;p为实际雷诺数。
从式(4)可以看出:对于某一特定的颗粒填充床,当填充床内流体的流态处于达西流区时,也就是此时流体处于低雷诺数时,式(4)右边第二项的值很小,可以忽略不计,即p为一恒定值,此时,式(4)可改写为

因此,可以根据达西流区量纲一压力降p恒定不变这一特点,确定出达西流区的分区范围。当雷诺数逐渐增加时,由式(4)可以看出,量纲一压力降随着雷诺数的增加而线性增加,因此可根据曲线斜率的变化来确定出非达西区中Forchheimer区和湍流区的区域范围。
待填充床内流体不同流态区域确定后,可根据不同区域内流体压力降的变化范围,拟合出不同流态区域描述颗粒填充床层阻力特性的Ergun修正关联式。
1.2 实验装置
气固流动实验装置如图1所示。实验竖罐的横截面为圆形,其内径和高度分别为450 mm和 1 400 mm,在竖罐本体外壁高度400,700和1 200 mm处各有1个测压孔,用来测量此处空气穿过料层的压力值。空气在鼓风机的驱动下,经过调节阀和孔板流量计后进入竖罐料层内,最后从竖罐顶部流出。实验通过调节阀来控制进入竖罐内的空气流量,通过孔板流量计来测量空气流量,通过压力数显表对实验过程中不同位置处的压力进行检测。实验所用烧结矿颗粒直径和形状因子[23],以及床层几何因子和空隙率[24]的变化范围如表1所示。实验过程中,烧结矿床层内空气的温度保持在20 ℃。

图1 气固流动实验装置示意图

表1 烧结矿颗粒相关参数
综合考虑影响烧结矿竖罐内气体流动特性的因素可分为2方面:一是床层因素,另一个是流动介质因素。床层因素包含:烧结矿形状因子,床层空隙率(通过颗粒尺寸来反映);流动介质因素包含:气体表观流速以及流体(动力)黏度。本文综合考虑了颗粒直径和气体表观流速对烧结矿床层内气体流动特性的影响。实验内容可分为2个方面:一方面,首先测量出不同空气流量和不同颗粒直径条件下空气穿过烧结矿床层的压力降,然后采用Ergun型方程量纲一化的方法确定不同烧结矿颗粒直径条件下的流态区域,得出不同流态区域间的临界雷诺数;另一方面,待临界雷诺数确定后,根据不同流态区域内空气压力降的变化范围,拟合出不同流态区域描述颗粒烧结矿填充床层阻力特性的Ergun修正关系式。
2 实验结果及分析
2.1 床层内气体压力降的变化
实验过程中自小到大调节实验竖罐进口空气流量,测定不同烧结矿颗粒直径条件下不同床层高度处的静压力差,然后取其平均值,得出填充床内空气单位高度压力降随气体表观流速和颗粒直径变化示意图,如图2所示。

dp/mm:1—6;2—14;3—24;4—35。
由图2可知:对于特定烧结矿颗粒直径填充床,空气表观流速越大,空气穿过床层的单位高度压力降变化就越大。以p=14 mm的颗粒填充床为例,通过实验数据拟合,得出气体压力降随表观流速的变化关系如下式所示。

由式(9)可知:单位料层高压力损失与颗粒表观流速呈二次方关系,符合Ergun提出的多孔介质内单相流压力降为流体表观速度的一次项和二次项之和的观点。其他颗粒直径填充床内空气压力降也符合这一观点。这一结论说明烧结矿填充床内描述空气压力降的关联式可以用Ergun型方程进行表示。
为了更清晰地表述颗粒直径对床层内空气压力降的影响,选取空气流量为600,800和1 000 m3/h条件下的实验数据作为参考值,得出床层内空气单位料层高压力降随颗粒直径变化示意图,如图3所示。

Q/(m3∙h−1):1—600;2—800;3—1 000。
由图3可知:对于特定空气流量,也就是空气表观流速一定时,烧结矿颗粒直径越小,床层内空气单位料层高压力降增加趋势就越大。以空气流量=800 m3/h为例,通过实验数据拟合,得出气体压力降随颗粒直径的变化关系如下式所示。
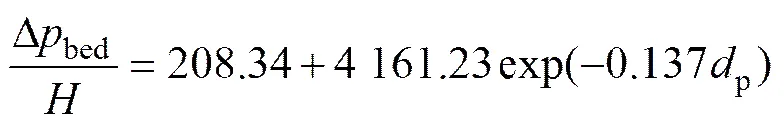
由式(10)可知:床层内空气单位料层高压力降随颗粒直径的增大而呈指数关系衰减。这是由于,当竖罐内径一定时,颗粒直径的增大会导致床层空隙率的增大[22],而描述空气压力降的Ergun型关联式中气体表观速度的一次项和二次项系数均随颗粒直径和床层空隙率的增大而急剧减小。因此,当空气表观流速不变时,颗粒直径越大,空气单位料层高压力降减小的就越快。
2.2 床层内气体流态的判定
根据图2中给出的不同工况下床层内空气压力降的实验数据,依据式(5)和(7),可得出不同烧结矿颗粒直径填充床内空气量纲一压力降p随雷诺数p变化的关系示意图,如图4所示。
由图4可知:随着雷诺数p的增加,量纲一压力降p随雷诺数p之间变化关系曲线,以点为分界点呈现不同的变化规律,即曲线斜率发生变化。而在低雷诺数段,并没出现量纲一压力降p趋近平缓的现象,即p不随雷诺数的增加而变化。由此可以说明,当气体表观流速>0.383 m/s,烧结矿填充床内空气流态已处于非达西流区。在实际操作过程中,考虑到烧结矿显热回收和冷却性能等问题,烧结矿床层内不会出现气体表观流速低于0.383 m/s的情况。为此,在本实验条件下,根据文献[21−22]得出的结论,可将烧结床层内非达西流区划分为2个区域:Forchheimer流动区域和Turbulence流动区域,并且由图4即可以确定出4种烧结矿颗粒直径填充床内Forchheimer流区和湍流区转折点所对应的临界雷诺数p,c分别为:p,c=532.95(图4(a))、p,c=1 871.2(图4(b))、p,c= 2 756.4(图4(c))和p,c=4 493.7(图4(d))。p,c变换为Re后,不同颗粒床层内Re分别为:Re=307.5(图4(a))、Re=1 047.9(图4(b))、Re=1 405.8 (图4(c))和Re=2 111.9(图4(d))。
由图5可以看出:床层内临界颗粒雷诺数Re随颗粒当量直径p的增大而逐渐增大,对Re实验值进行数据拟合,即可得到床层内非达西流区转折点所对应的临界颗粒雷诺数Re随颗粒当量直径变化的实验关联式:

由式(11)可知:床层内临界颗粒雷诺数Re与颗粒当量直径呈现出三次方变化关系,并且该公式的预测值和实验值之间的相对误差在±5%以内。由于本实验中,烧结填充床内颗粒当量直径的最小值为3.78 mm,因此,颗粒当量直径小于3.78 mm的床层内临界颗粒雷诺数不能通过本实验的数据分析得出。但基于本实验所围绕的烧结余热竖罐内颗粒的填充特点,较小的颗粒当量直径可不作考虑。
p/mm:(a) 6;(b) 14;(c) 24;(d) 35
图4 床层内空气量纲一压力降p随雷诺数p变化示意图
Fig. 4 Change schematic of air dimensionless pressure drop in bed layer with Reynolds number

图5 临界颗粒雷诺数随颗粒当量直径变化示意图
2.3 压力降实验关联式的确定
目前已提出许多物理模型对颗粒填充床内流体的压力降进行预测[9−18]。模型通常将球体颗粒或均匀颗粒作为研究对象,并没有考虑非均匀颗粒的形状因子对床层内流体压力降的影响。同时,不同流体介质和颗粒直径所对应的颗粒填充床内流体的阻力特性也不一样[15−18]。另外,不同颗粒雷诺数时,床层内流体所处的流态区域也不尽相同,导致不同流态区域内流体的压力降预测关联式也不一样[21−22]。因此,根据所得不同工况下的实验数据,需要对非均匀烧结矿床层内流体压力降的实验预测关联式进行重新计算。
在确定床层内流态分区的基础上,利用Ergun型方程模型对实验数据进行分区拟合,得到不同颗粒直径和不同流动区间内Ergun型经验公式系数,如表2所示。

表2 分区拟合得到Ergun型方程经验系数
由表2可以看出:由于颗粒直径和流态区域的不同,所得到的Ergun型方程经验系数1和2也不相同,并且1和2随着颗粒直径的增大而增大。考虑到床层几何因子/p对床层空隙率和边壁效应的影响[24],Ergun型方程系数1和2与床层几何因子/p之间关系分别如图6和图7所示。

图6 k1与D/dp关系拟合曲线

图7 k2与D/dp关系拟合曲线
根据图6和图7可得烧结矿填充床内Ergun型方程系数1和2分别为:
1) Forchheimer流动区域:

(13)
2) Turbulence流动区域:

(15)
式中:为罐体床层直径,m;p为床层几何因子。
由式(12)~(15)可知:不同流态区域内,1和2随床层几何因子的增大而呈指数关系衰减,并逐渐趋于平缓。将式(12)和(13)或式(14)和(15)分别代入式(3)中可得冷态工况下描述烧结矿床内气体压力降的Ergun型方程。
1) Forchheimer流动区域:

(16)
2) Turbulence流动区域:

(17)
床层内流体的流态可根据式(11)进行判定。另外,式(16)和(17)的预测值和实验值之间的相对误差均在±8%以内,能够很好地预测烧结矿填充床内空气的压力降。
考虑到热态工况时,气体的密度和动力黏度都会发生变化。为此,针对式(16)和式(17)引入气体状态方程,将式中各参数转换成本实验工况下的值。首先,无论以何种状态作为基准,流过床层的质量流量保持不变,所以

式中:0为热态工况气体密度,kg/m;0为热态工况气体表观流速,m/s;为实验工况下气体密度,kg/m;为实验工况下气体表观流速,m/s。
根据气体状态方程,床层内热态工况下与实验工况下气体状态参数之间关系为

式中:为实验工况下测量高度的平均压力,Pa;0为热态工况条件下测量压力,Pa;为实验工况下大气温度,K;0为热态工况下气体温度,K。
将式(19)代入式(16)和(17)中可得热态工况下描述烧结矿床内气体压力降的Ergun型方程。
1) Forchheimer流动区域:

(20)
2) Turbulence流动区域:

(21)
3 结论
1) 气体表观流速和颗粒直径对床层内空气的压力降有重要影响。当颗粒直径一定时,随着气体表观流速的增大,床层内空气单位料层高压力降与气体表观流速呈二次方关系增大。当气体表观流速一定时,由于竖罐床层内径不变,颗粒直径的增大会使得床层空隙率增大,导致床层内空气单位料层高压力降随颗粒直径的增大而呈指数关系衰减。
2) 根据非达西流区量纲一压力降曲线斜率的变化,得到烧结矿床层内临界颗粒雷诺数随颗粒当量直径变化的实验预测关联式,相对误差在±5%以内。由关联式可知,床层内临界颗粒雷诺数随颗粒当量直径的增大呈三次方关系增大。
3) 在确定床层内流态分区的基础上,对颗粒填充床内描述流体压力降的Ergun型方程进行修正,分别得到冷态工况下烧结矿床层内Forchheimer流区和湍流区的压力降实验预测关联式,相对误差均在±8%以内,表明所得实验关联式具有良好的预测性能。
4) 当烧结矿颗粒有温度变化过程时,引入气体状态方程对冷态工况条件下的气体压力降实验关联式进行修正,得到了热态工况条件下烧结矿床层内Forchheimer流区和湍流区的压力降实验预测关联式。
[1] 蔡九菊, 王建军, 陈春霞, 等. 钢铁工业余热资源的回收与利用[J].钢铁, 2007, 42(6): 1−7. CAI Jiuju, WANG Jianjun, CHEN Chunxia, et al. Waste heat recovery and utilization in iron and steel industry[J]. Iron and Steel, 2007, 42(6): 1−7.
[2] 董辉, 赵勇, 蔡九菊, 等. 烧结−冷却系统漏风问题研究[J]. 钢铁, 2012, 47(1): 95−99. DONG Hui, ZHAO Yong, CAI Jiuju, et al. On the air leakage problem in sintering cooling system[J]. Iron and Steel, 2012, 47(1): 95−99.
[3] MARCELO R E, LUIZ F M. Thermodynamic analysis of a coke dry quenching unit[J]. Energy Conversion & Management, 2000, 41(2): 109−127.
[4] DONG H, JIA F R, ZHAO Y, et al. Experimental investigation on the drying process of the sinter mixture[J]. Powder Technology, 2012, 218: 1−4.
[5] 蔡九菊, 董辉. 烧结过程余热资源的竖罐式回收与利用方法及其装置: 200910187381.8[P]. 2009−09−15. CAI Jiuju, DONG Hui. The method and device of sintering waste heat recovery and utilization with vertical tank: 200910187381.8[P]. 2009−09−15.
[6] 董辉,李磊,刘文军,等. 烧结矿余热竖罐式回收利用工艺流程[J]. 中国冶金, 2012, 22(1): 6−11. DONG Hui, LI Lei, LIU Wenjun, et al. Process of waste heat recovery and utilization for sinter in vertical tank[J]. China Metallurgy, 2012, 22(1): 6−11.
[7] ALBUSAIRI B, HSU J T. Application of shape factor to determine the permeability of perfusive particles[J]. Chemical Engineering Journal, 2002, 89(1/2/3): 173−183.
[8] TENG H, ZHAO T S. An extension of Darcy’s law to non-stokes flow in porous media[J]. Chemical Engineering Science, 2000, 55(14): 2727−2735.
[9] ERGUN S, ORNING A A. Fluid flow through randomly packed columns and fluidized beds[J]. Industrial and Engineering Chemistry Research, 1949, 41(6): 1179−1184.
[10] ERGUN S. Fluid flow through the packed columns[J]. Chemical Engineering Progress, 1952, 48: 89−94.
[11] ROSE H E. On the resistance coefficient–Reynolds number relationship for fluid flow through beds of granular materials[J]. Proceedings of the Institution of Mechanical Engineers, 1945, 153: 154−168.
[12] HICKS R E. Pressure drop in packed beds of spheres[J]. Industrial and Engineering Chemistry Research Fundamentals, 1970, 9 (3): 500−502.
[13] LEE J S, OGAWA K. Pressure drop through packed beds[J]. Journal of Chemical Engineering of Japan, 1974, 27(5): 691−693.
[14] MONTILLET A, AKKARI E, COMITI J. About a correlating equation for predicting pressure drops through packed beds of spheres in a large of Reynolds numbers[J]. Chemical Engineering and Processing, 2007, 46(4): 329−333.
[15] MACDONALD I F, EL-SAYED M S, MOW K, et al. Flow through porous media: the Ergun equation revisited[J]. Industrial and Engineering Chemistry Research Fundamentals, 1979, 18(3): 199−208.
[16] 蔡九菊, 饶荣水, 于庆波, 等. 填充球蓄热室阻力特性实验研究[J]. 钢铁, 1998, 33(6): 57−60. CAI Jiuju, RAO Rongshui, YU Qingbo, et al. Experimental study on resistance of packed ball regenerator[J]. Iron and Steel, 1998, 33(6): 57−60.
[17] TAN K K, SAM T, JAMALUDIN H. The onset of transient convection in bottom heated porous media[J]. International Journal of Heat and Mass Transfer, 2003, 46(15): 2857−2873.
[18] OZAHI E, GUNDOGDU M Y, CARPINLIOGLU M Ö. A modification on Ergun’s correlation for use in cylindrical packed beds with non-spherical particles[J]. Advanced Powder Technology, 2008, 19(4): 369–381.
[19] RODE S, MIDOUX N, LATIFI M A, et al. Hydrodynamics of liquid flow in packed beds: an experimental study using electrochemical shear rate sensors[J]. Chemical Engineering Science, 1994, 49(6): 889−900.
[20] SEGUIN D, MONTILLET A, COMITI J. Experimental characterization of flow regimes in various porous media. I: limit of laminar flow regime[J]. Chemical Engineering Science, 1998, 53(21): 3751−3761.
[21] FAND R M, KIM B Y K, LAM A C C, et al. Resistance to the flow of fluids through simple and complex porous media whose matrices are composed of randomly packed spheres[J]. Journal of Fluids Engineering, 1987, 109(3): 268−273.
[22] KECECIOGLU I, JIANG Y X. Flow through porous media of packed spheres saturated with water[J]. Journal of Fluids Engineering, 1994, 116(1): 164−170.
[23] GELDART D. Estimation of basic particle properties for use in fluid-particle process calculations[J]. Powder Technology, 1990, 60 (1): 1−13.
[24] 冯军胜, 董辉, 曹峥, 等. 烧结竖罐床层内的空隙率分布特性[J]. 中南大学学报(自然科学版),2016, 47(1): 8−13. FENG Junsheng, DONG Hui, CAO Zheng, et al. Voidage distribution properties of bed layer in sinter vertical tank[J]. Journal of Central South University (Science and Technology), 2016, 47(1): 8−13.
(编辑 杨幼平)
Gas flow characteristics in vertical tank for sinter waste heat recovery
FENG Junsheng, DONG Hui, LI Hanzhu, GAO Jianye
(SEP Key Laboratory on Eco-industry, School of Metallurgy, Northeastern University, Shenyang 110819, China)
The dimensionless method of Ergun’s type equation was used to investigate pressure drop and flow regime of gas flow through bed layer. The effects of gas superficial velocity and sinter particle diameter on pressure drop and flow regime were studied. The results show that for a given particle diameter, pressure drop of unit bed layer height in sinter bed layer increases as a quadratic relationship with increasing gas superficial velocity. For a given gas superficial velocity, pressure drop of unit bed layer height increases as an exponential relationship with the increase of particle diameter. Experimental correlation is proposed for predicting the change of critical particle Reynolds number with particle equivalent diameter, and the deviation of the correlation is within ±5%. Experimental correlations are proposed for predicting pressure drop of Forchheimer zone and Turbulence zone in bed layer, and the deviations of the correlations are all within ±8%, showing good prediction.
sinter; packed bed; pressure drop; flow regime; critical Reynolds number
10.11817/j.issn.1672-7207.2017.01.001
TK11+5
A
1672−7207(2017)01−0001−08
2016−01−24;
2016−04−03
国家自然科学基金资助项目(51274065);辽宁省科技计划项目(2015020074-201) (Project(51274065) supported by the National Natural Science Foundation of China; Project(2015020074-201) supported by the Science and Technology Planning Foundation of Liaoning Province, China)
董辉,教授,博士生导师,从事冶金过程余热余能高效回收利用研究;E-mail: Dongh@smm.neu.edu.cn

