岩石随机孔隙结构的三维重构模型与细观渗流分析

赵延林，曹平，唐劲舟，马文豪，李树清，王卫军



岩石随机孔隙结构的三维重构模型与细观渗流分析

赵延林1, 2，曹平3，唐劲舟1，马文豪1，李树清1，王卫军1

(1. 湖南科技大学煤矿安全开采技术湖南省重点实验室，南方煤矿瓦斯与顶板灾害防治安全生产重点实验室，湖南湘潭，411201；2. 中国矿业大学煤炭资源与安全开采国家重点实验室，江苏徐州，221008;3. 中南大学资源与安全工程学院，湖南长沙，410083)

将多孔岩石介质的孔隙视为具有毫米量级的随机细观结构，重构岩石三维随机孔隙结构模型，在细观力学的层面上研究孔隙结构对多孔岩石渗流的影响。引入微管渗流模型，利用统计学原理和FLAC3D软件研究多孔岩石介质随机孔隙结构的重构技术和细观渗流数值模拟方法。研究结果表明：多孔岩石孔隙率越大，流体由非稳定流过渡到稳定流的时间愈短，渗透系数和孔隙率具精度很高的线性关系，岩石介质透水性的孔隙率阈值λ=4.05%，峰前多孔岩石介质的渗透系数主要受体积应力控制，且两者之间具有负指数关系。重构毫米量级的孔隙结构单元，其数值稳定性可以得到保证。

岩石力学；孔隙结构；细观渗流；流固耦合；重构模型

流体通过多孔介质的渗透是许多工程学科的基础。岩石是一种天然的多孔介质，其内部包含着大量不规则、跨尺度的孔隙。研究孔隙结构对渗流特性的影响对于揭示岩石损伤破裂、流固耦合行为的细宏观机理有重要的理论意义和工程应用价值[1−2]。孔隙结构对多孔岩石介质渗透特性产生很大影响。CLAVAUD等[3]分析了不同岩石的孔隙几何结构对渗透率的各向异性的影响，发现砂岩渗透率的各向异性与砂岩固有的层理密切相关，而火山岩的渗透率的各向异性则与孔隙或者裂隙的方位有关。仵彦卿等[4]通过CT 尺度砂岩渗流与应力关系试验研究，发现岩石的渗流取决于其内部孔隙结构的变化。黄先伍等[5]基于破碎砂岩稳态渗透试验得到了渗透率、非Darcy流因子与孔隙率之间的幂函数拟合关系。岩石渗透系数受所处的应力环境的影响。LOUIS[6]根据坝基渗流实验结果提出了渗透系数与应力的负指数耦合关系；赵阳升[7]在大量试验研究的基础上，引入等效孔隙压系数对LOUIS耦合公式进行了合理修正；叶源新等[8]根据理论分析和试验结果建立了孔隙型岩石的渗流应力耦合特性关系式，指出平均有效应力是控制孔隙型岩石渗透系数变化的主要因素。目前，人们对于岩石(体)渗流的宏观流固耦合响应进行了大量的研究而且取得不少研究成果[9−11]，但对于微细层次上的渗流和流固耦合机理的研究积累极少。由于岩石孔隙结构形态复杂且无序分布，再加上目前理论和试验手段的限制，还无法准确地描述岩石内部孔隙结构分布特征，并难以从理论上建立孔隙结构与岩体渗流性质之间的关系。孔隙岩石仍像1个“黑箱”，人们更多关注的是各种表观力学和渗流过程经过这个“黑箱”后的变化，无法定量解析孔隙连通性、流体渗流路径以及流体与孔隙相互作用等对岩体渗流性质起控制作用的内部微细观机制，难以直观、准确地描述孔隙结构并建立这种描述与流体渗流性质之间的内在联系[12]。近些年来，研究者开始寻求天然岩石孔隙结构的三维数值模型即岩石孔隙结构的三维重构，并以此为基础来定量地分析孔隙结构与岩石渗流特性之间的内在关系。LOCK等[13]应用二维图像分析岩石孔隙结构特征，提出了立方体网络的孔隙管模型，用以预测沉积岩岩芯的渗透率；OKABE等[14]基于孔隙岩石的二维切片试验，利用多点统计方法建立了三维孔隙模型，模拟研究了孔隙岩石多相流问题。王金波等[15]基于改进的随机堆积球法，提出了岩石孔隙结构的三维重构方法以研究气体在孔隙岩石内部的渗流行为。通过构建岩石孔隙结构三维模型，并进行渗流分析为打开多孔岩石这个“黑箱”，揭示一系列物理力学化学过程中影响多孔岩石表观性质的复杂内在机制开辟了一条新的途径。本文作者基于细观渗流力学尺度将多孔岩石孔隙视为具有毫米量级的细观结构，重构多孔岩石随机三维孔隙结构，在细观力学的层面上研究孔隙结构对多孔岩石介质渗流的影响。

1 随机岩石孔隙结构三维重构

1.1 岩石(体)渗流研究尺度

宏观尺度的渗流研究是以岩体为研究对象，研究流体在岩体介质内的宏观流动规律及流固耦合响应。在进行渗流计算时，计算的尺度多在千米级，称为宏观水平，它是渗流力学服务于岩体工程的尺度。在宏观尺度下不考虑多孔介质孔隙的形态、分布规律等微观特性，而注重于对岩体裂隙分析、裂隙流量、岩体裂隙渗透系数等宏观渗流力学参数的描述。

微观层次的渗流关注多孔介质体系内流体的流动细节，考虑多相流体之间以及流体与多孔介质表面之间的相互作用，这个层次上的流动发生在微米级尺度上，称为微观孔隙水平，它是渗流力学研究的基础。

本文探讨多孔岩石介质的随机孔隙结构的重构技术，重构的孔隙结构的孔径、体积尺度在毫米量级上。重构的孔隙结构介于宏观尺度和微观尺度之间，可以认为一种细观尺度。

1.2 随机孔隙结构重构

多孔岩石介质中孔隙结构的分布是随机的，假定孔隙在多孔岩石中的位置满足均匀分布，在FLAC3D下三维孔隙结构的随机重构技术可按如下步骤实现。

1) 多孔岩石介质建模。确定重构模型的尺寸，设定孔隙结构的平均孔径，并以此为依据设置模型网格划分精度，以保证每个划分单元的尺寸与孔隙结构的平均孔径相吻合。

2) 在FLAC3D下基于FISH语言编写[1，]的均匀随机整数序列的生产程序。生成个1到之间的均匀分布随机整数序列。其中为计算模型中的网格数目。

3) 将产生的随机整数序列作为网格单元的编号(ID)，将其视为孔隙结构单元，统计所有孔隙结构单元的体积m，则计算模型的孔隙率可由下式得到：

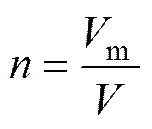
式中：为计算模型单元的总体积。

4) 孔隙和非孔隙单元的赋值。力学分析时将孔隙结构单元设置为model null，将非孔隙单元设置为model mohr；渗流分析时将孔隙结构单元设置为model fl_ iso，而将非孔隙单元视为不透水边界，设置为model fl_ null。

在试验室内岩石的强度和渗透试验大多采用直径×高度为50 mm×100 mm圆柱体试件。重构出来的多孔岩石数值试件应与试验室所用试件尺寸相一致，以方便校核数值研究与试验结果之间的误差。因此，重构多孔岩石试件设定直径×高度为50 mm× 100 mm圆柱体试件。通过设置不同的，获得不同孔隙率的多孔岩石数值试件。运用三维随机孔隙结构的重构技术得到不同孔隙率下岩石孔隙的细观结构及随机分布。图1所示为在孔隙结构细观体积为1.38 mm3条件下，孔隙率分别为3%和19%的多孔岩石试件孔隙结构的数值重构图。

从图1可以看出：当孔隙率=3%时，孔隙结构随机分布于试件中，孔隙连通性较差。当孔隙率=19%时，孔隙结构单元数目远比孔隙率=3%时的大，孔隙连通良好。

(a) 孔隙率n=3%时孔隙分布；(b) 孔隙率n=3%时过试件轴线的剖面；(c) 孔隙率n=19%时孔隙分布；(d)孔隙率n=19%时过试件轴线的剖面

2 多孔岩石介质细观渗流分析

2.1 微管渗流模型

设长为，断面积为的长方体多孔岩石介质的孔隙率为i，将其全部孔隙空间等效为根长为、直径为i的平行等径微管，简化后的“假想岩石”如图2所示。假设多孔介质的渗流通过介质中微管流动，渗径为试件长度。微管的水力梯度i根据渗透压的变化而变化。在稳定渗流的状态下，微管中的流速i可以表示为

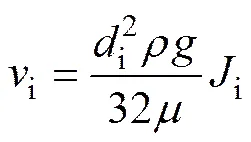
微管的表观渗透系数i为

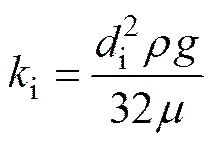
仵彦卿等[4, 16]通过对CT 尺度砂岩渗流与应力关系的试验研究及结果分析得出：微管的表观直径的数量为10−6~10−7 m，若取微管的表观直径i=6.5×10−7m，则由式(3)得微管的表观渗透系数约为

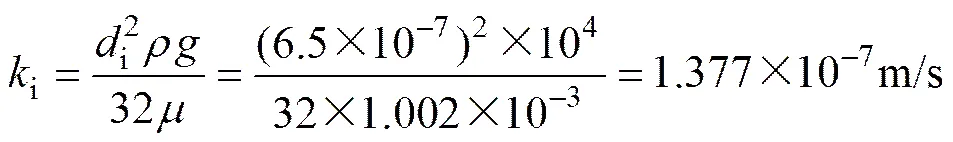
2.2 孔隙率对多孔岩石介质渗透系数的影响

为研究孔隙结构对多孔岩石渗透特性的影响，探讨岩石渗透系数与孔隙率的相依关系，构建不同孔隙率下的多孔岩石试件的渗流数值模型。采用FLAC3D的渗流模块，对数值试件进行渗流分析。

1) 计算模型。数值计算模型见图3。多孔岩石介质计算模型的直径×高度为50 mm×100 mm圆柱体，孔隙结构单元的平均细观体积设定为1.38 mm3。试件上表面固定水压力1=1 MPa，下表面固定水压力2=0.1 MPa。孔隙结构单元的渗透系数等同于微管的表观渗透系数i。在数值计算中，通过记录上、下表面内全部孔隙单元的流量，结合数值试件的尺寸，不同孔隙率时多孔岩石介质的宏观渗透系数为

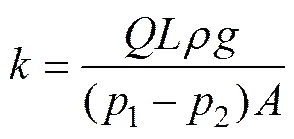
式中：为过上、下表面内全部孔隙单元的流量；为试件长度；1和2分别为试件上、下表面的固定水压；为试件上、下表面的面积。

2) 结果分析。当孔隙率为3%~23%之间，取若干不同孔隙率分别进行渗流分析。渗流计算发现当孔隙率=3%时，试件内孔隙结构单元无连通团，流体无法从一端渗入另一端，孔隙率=3%的岩石试件不具有渗透性。图4所示为孔隙率=3%时，试件的孔隙压分布。由于试件上、下表面之间无孔隙连通团，流体无连通的渗流路径，从而无法渗透过试件。随着孔隙率减小，孔隙结构单元的连通性越差，可以认为在孔隙结构单元平均细观体积为1.38 mm3的条件下，当孔隙率≤3%时，岩石不具有渗透性。

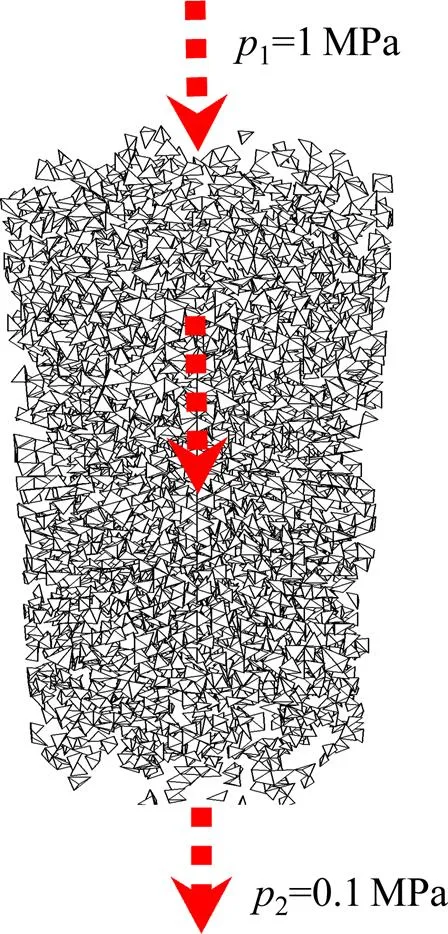
图3 三维随机孔隙细观渗流计算模型

图4 孔隙率n=3%时试件孔隙压分布

图5所示为孔隙率=5%时的孔隙水压的分布。当孔隙率=5%时，流体通过连通的孔隙结构通道中从试件上表面渗流至下表面，孔隙连通团可将高水压和低水压沟通，从而形成稳定的多孔介质渗流。

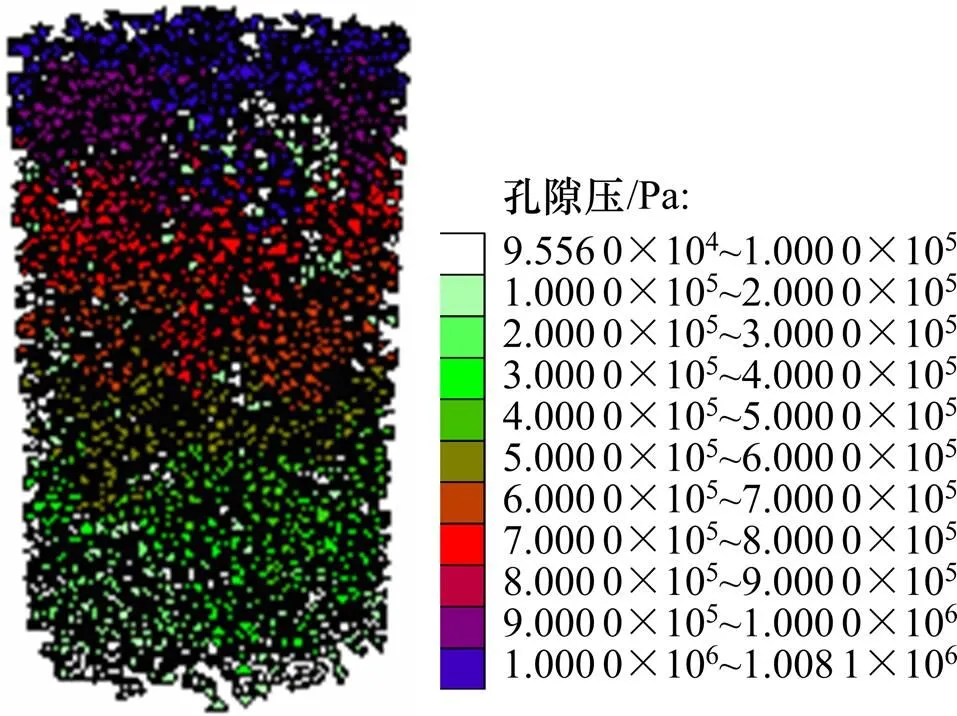
图5 孔隙率n=5%下试件孔隙压分布

为探讨多孔岩石介质具有透水性的孔隙率阈值，在孔隙率为3%~5%时，采用二分法对不同孔隙率进行筛选优化数值分析。获得透水性的孔隙率阈值。ANSELMETTI等[17]采用数字图像分析定量描述碳酸盐岩孔隙体系，发现渗透率主要受大孔隙(孔径大于20 μm的孔隙)之间连通性控制，碳酸盐岩连通的大孔隙是流体主要流动通道。ANSELMETTI等[17]研究认为大孔隙率4%是连通大孔隙控制渗流的门槛值，当大孔隙率小于4%时，流体无法通过大孔隙渗流。本文采用岩石随机孔隙结构的三维重构模型，重构的孔隙结构孔径在毫米量级(大于20 μm)属于大孔隙结构，其岩石透水性的孔隙率阈值，这与ANSELMETTI等[17]的实验研究结果基本吻合。这在一定程度上表明用三维重构模型研究多孔岩石介质的细观渗流规律是可行的。

随着孔隙率增大，连通孔隙结构团体积增大，通过连通团的流量随之增加。图6所示为不同孔隙率下多孔岩石试件流量随渗流时间的变化曲线。从图6可见：孔隙率越大，由非稳定流过渡到稳定流的时间越短，通过断面的流量也愈大。连通孔隙结构团为水流动提供了通道，孔隙率越大，连通孔隙结构团越多，渗流的阻力愈小，因此，流体由非稳定流过渡到稳定流的时间愈短。计算得出孔隙率为23%和5%的非稳定流历时分别为69.4 h和125.0 h。这一结论对于油气储量预测、地下水开发的抽采时间的把握具有一定的指导作用。

将不同孔隙率试件的流量代入式(5)，得到不同渗透率试件的渗透系数。图7所示为多孔岩石介质渗流系数与孔隙率的关系曲线。发现在有效孔隙率的范围内(≥4.05%)渗透系数和孔隙率具精度很高的线性关系。数值试验得到渗流系数(单位为m/s)与孔隙率的关系式可用下式表示：

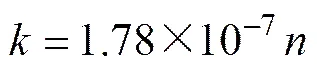
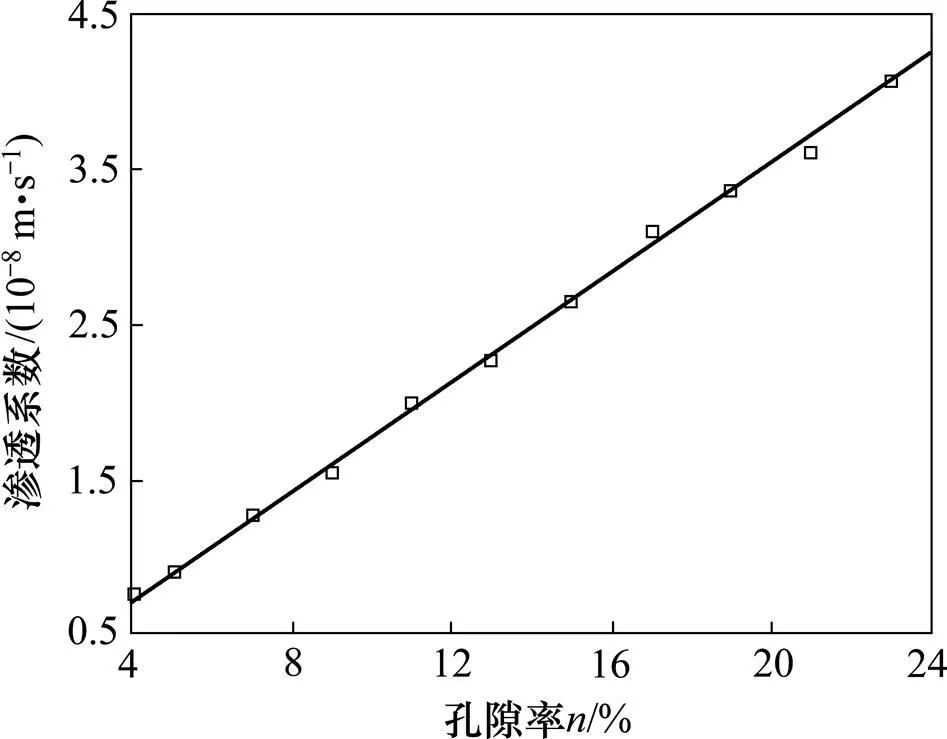
图7 渗透系数随孔隙率的变化曲线

2.3 多孔岩石介质渗透系数的流固耦合方程

多孔岩石介质渗透系数和岩体工程所处的应力水平密切相关，通过对重构模型施加轴向应力和环向应力，可得到不同应力水平下的孔隙结构单元的体积变化；提取不同应力状态下的孔隙结构单元，并对其进行渗流分析，从而得到不同应力状态下多孔岩石介质的渗透系数。以孔隙率=5%和19%为例，从细观力学角度研究多孔岩石介质渗透数和应力水平的关系。

图8所示为多孔岩石试件所处的应力状态的计算模型。试件环向施加围压，试件上下表面施加轴压。数值计算中采用3种不同的围压即1，3和6 MPa，逐步增加轴压，即增加试件的体积应力。数值计算参数如下：岩石弹性模量=10 GPa；泊松比；内摩擦角40°；内聚力=2.5 MPa。调用FLAC3D中的Mohr–Coulomb模型，通过设置大变形模型，跟踪各孔隙单元的体积变化，并其换算成孔隙率的变化，通过对不同围压下的数值模拟，发现峰前多孔岩石介质孔隙率主要受体积应力影响。本数值模型中体积应力用下式表示：

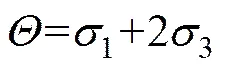
图8 计算模型及应力边界条件

Fig. 8 Calculation model and stress boundary condition

图9所示为当初始孔隙率0分别为5%和19%时，孔隙率随体积应力的演化曲线。由图9可知：随体积应力增大，孔隙体积逐步变小。对于初始孔隙率为5%的试件，加载至体积应力为40 MPa时，试件孔隙率变为4.67%；对于初始孔隙率为19%的试件，当加载至体积应力为40 MPa时，试件孔隙率变为17.2%。

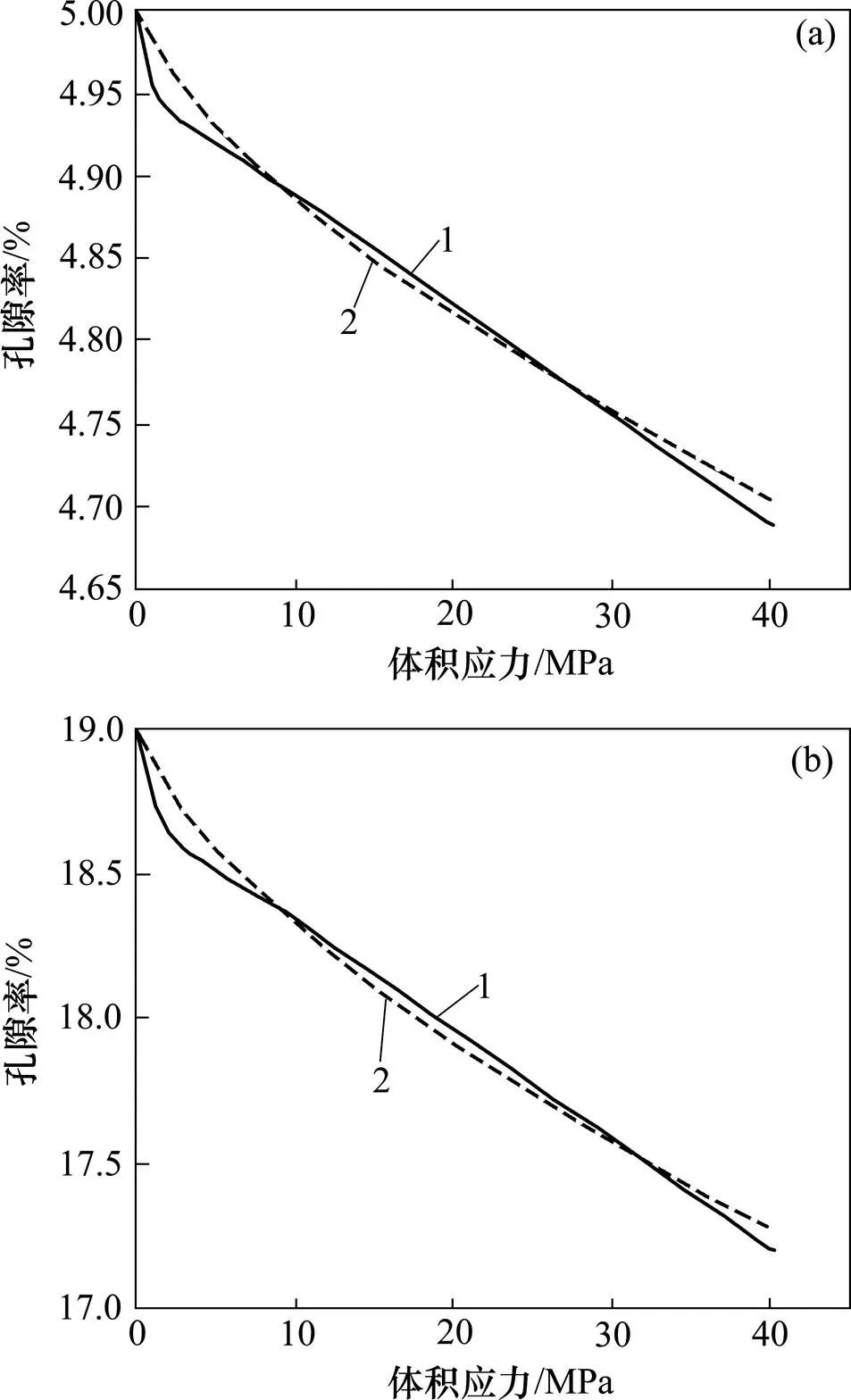
(a) 初始孔隙率n0=3%；(b) 初始孔隙率n0=19%

采用幂函数对体积应力作用下孔隙率的变化进行拟合，得到体积应力作用下峰前多孔岩石介质孔隙率的变化规律：

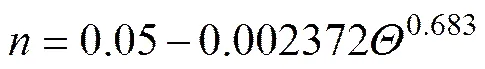
，当0=19%时(9)

体积应力的增加使孔隙率减少，导致多孔介质的孔渗微观通道—微管体积减少，微管直径变窄。根据孔隙率的变化可反演出微管直径的变化。

初始状态下，微管体积0为

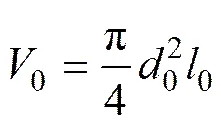
式中：0为微管初始直径；0为微管初始长度。

在体积应力作用下，导致微管体积变为1：

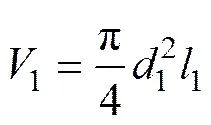
式中：1为体积应力作用下微管直径；1为体积应力作用下微管长度。

将式(10)和式(11)相比，得

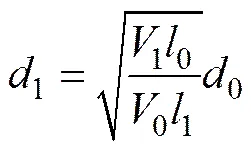
微管径向变形对微管体积的影响要远大于微管轴向变形的影响，在式(12)中可近似取。

在体积应力作用下，孔隙压缩而导致微管直径变窄，进而影响微管的表观渗透系数，体积应力作用下微管的表观渗透系数1表示为

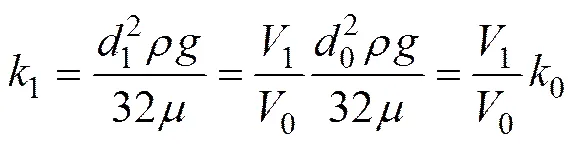
体积应力的增加使孔隙率减少，流体的过水通道的体积减少而导致岩石渗透性降低，而更主要的是由于体积应力导致微管直径变小，从而导致微管的表观渗透系数降低。

在数值分析中通过提取峰前不同应力状态的孔隙结构单元进行渗流分析，其中孔隙结构单元的渗透系数随孔隙率的变化采用式(13)。图10所示为数值实验获到的孔隙率=19%，不同围压下渗透系数随体积应力的变化曲线。由图10可知：在体积应力一定的条件下，围压对渗透系数有一定的影响，随围压增加多孔岩石渗透系数减少，但在不同围压条件下，只要体积应力()恒定，尽管随围压增加，渗透系数减少，但这种减少趋势并不显著(见图10)。渗透系数主要受体积应力控制，对不同围压下的渗透系数进行平均化处理，得到峰前多孔岩石介质渗透系数和体积应力之间的关系，并采用负指数函数对曲线进行拟合得

式中：0为多孔岩石介质的初始渗透系数。

结合式(6)和(14)，峰前多孔岩石介质的渗透系数与孔隙率、体积应力的关系可表示为

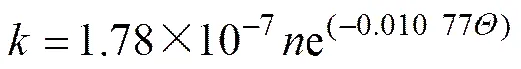
式(14)和(15)表征了多孔岩石介质的渗系数和体积应力的负指数关系。渗透系数和体积应力的负指数关系被大量岩石的渗透试验所验证[18−19]，本文从细观力学的角度出发，使这一经典关系式得到细观数值 验证。

图10 渗透系数随体积应力的变化曲线

Fig. 10 Change of seepage parameter with volumetric stress

2.4 孔隙结构渗透特性的网格稳定性

对于多孔岩石介质孔隙结构的重构，孔隙结构的细观单元必须足够小，才能使重构的孔隙单元能较准确地在细观力学层次上揭示多孔介质的渗流特性；另一方面，若孔隙结构尺寸过小，则计算工作量会急剧增加。为研究孔隙结构单元尺寸对计算结果的影响，采用6.51，3.43，2.15，1.38，0.69和0.37 mm36种不同的孔隙结构单元体积来探讨孔隙结构渗透特性的网格稳定性。下面以孔隙率=4%和19%为例来说明孔隙结构渗透特性的网格稳定性。

采用6个不同尺度的孔隙结构单元进行渗流分析，发现孔隙率=4%时，在6种不同的细观尺度下流体均无法透过试件，岩石不具有渗透性。图11所示为在孔隙结构细观尺度为0.37 mm3，孔隙率=4%时的孔隙水压的分布。由图11可以看出：当孔隙率=4% 时，由于缺少足够多的连通孔隙结构团，流体无法渗过试件。

当孔隙率=19%时，采用上述6种不同的细观尺度进行渗流分析，得到多孔岩石介质渗透系数与孔隙结构细观尺寸的相依关系见图12。由图12可知：孔隙单元体积为0.37~6.51 mm3时，渗透系数随单元体积的增大而稍有下降，但波动幅度很小，波动范围在0.2×10−8 m/s以内；当孔隙单元体积小于1.38 mm3时，多孔岩石的介质渗透系数几乎保持在3.367×10−8 m/s不变。这说明了重构的孔隙结构单元细观尺寸在毫米量级时，孔隙结构单元渗透特性的网格稳定性良好。

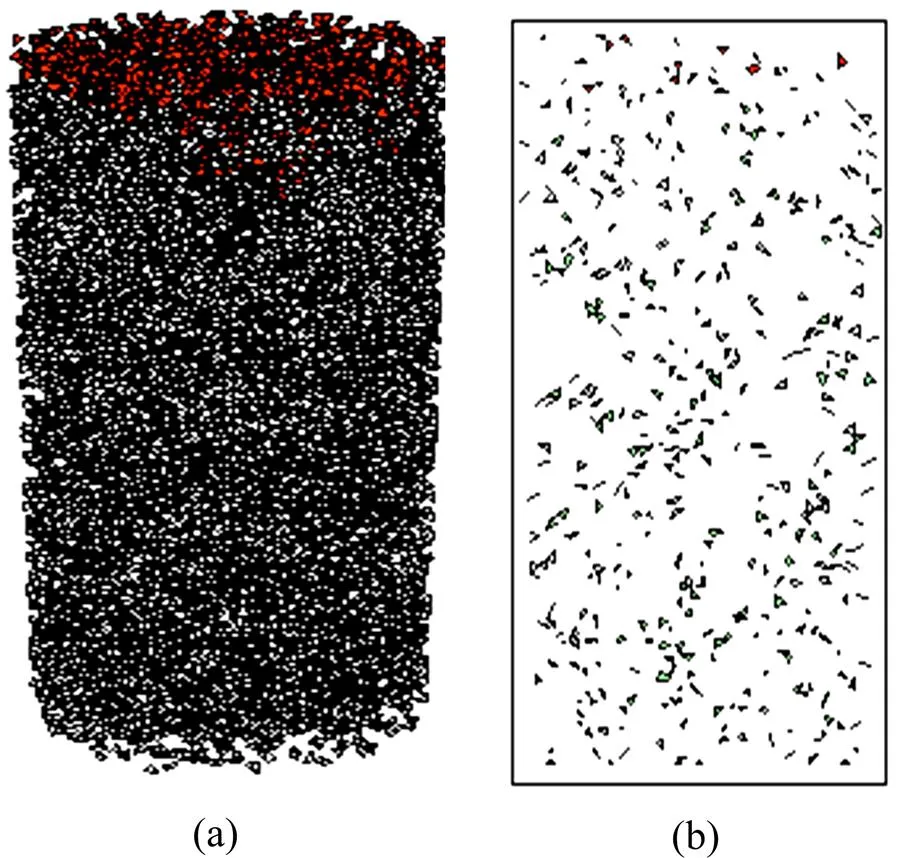
(a) 孔隙率n=4%孔隙压分布；(b)孔隙率n=4%时过试件轴线的剖面

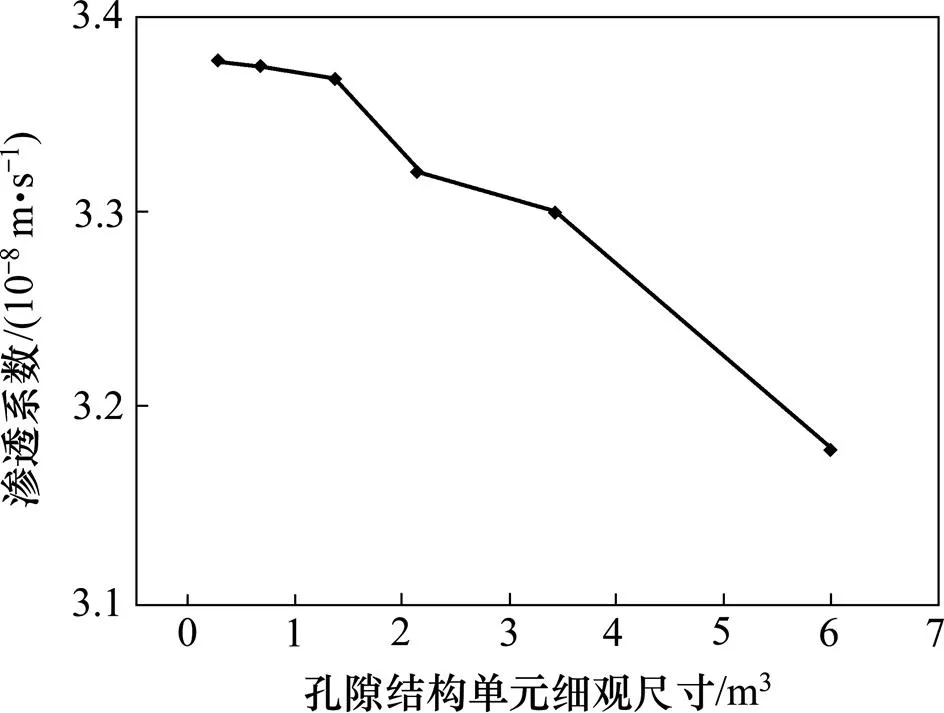
图12 孔隙率n=19%时渗透系数和孔隙单元尺寸的相关曲线

重构多孔岩石介质的孔隙结构研究岩石渗透的细观特性，其数值稳定性可以得到保证。该研究方法在理论和数值上验证多孔岩石介质渗透的流固耦合特性，为研究多孔介质渗流的细观行为、流固耦合细观力学响应提供了一条新的途径。

3 结论

1) 将岩石孔隙结构视为具有毫米量级的细观结构，重构岩石三维随机孔隙结构，在细观力学的层面上研究孔隙结构对多孔岩石渗流的影响。

2) 引入微管渗流模型，通过多孔岩石介质细观渗流分析，发现岩石孔隙率越大，流体由非稳定流过渡到稳定流的时间愈短，渗透系数和孔隙率具精度很高的线性关系，多孔岩石介质透水性的孔隙率阈值λ=4.05%。

3) 峰前多孔岩石介质的渗透系数主要受体积应力控制，渗透系数和体积应力之间具有负指数关系。

4) 当重构的三维随机孔隙单元的平均孔径在毫米量级时，孔隙单元渗透特性的网格稳定性较强。

[1] JU Y, YANG Y M, SONG Z D, et al. A statistical model for porous structure of rocks[J]. Science in China (Series E), 2008, 51(11): 2040−2058.

[2] ZHAO Y L, ZHANG L Y, WANG W J, et al. Transient pulse test and morphological analysis of single rock fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 91(1): 139−154.

[3] CLAVAUD J B, MAINEULT A, ZAMORA M. Permeability anisotropy and its relations with porous medium structure[J]. Journal of Geophysical Research (Part B), 2008, 113(B1): 1202−1212.

[4] 仵彦卿, 曹广祝, 丁卫华. CT尺度砂岩渗流与应力关系试验研究[J]. 岩石力学与工程学报, 2005, 24(23): 4203−4209. WU Yanqing, CAO Guangzhu, DING Weihua. Experimental study on relation between seepage and stress of sandstone in CT scale[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23): 4203−4209.

[5] 黄先伍, 唐平, 缪协兴, 等. 破碎砂岩渗透特性与孔隙率关系的试验研究[J]. 岩土力学, 2005, 26(9): 1385−1388. HUANG Xianwu, TANG Ping, MIAO Xiexing, et al. Testing study on seepage properties of broken sandstone[J]. Rock and Soil Mechanics, 2005, 26(9): 1385−1388.

[6] LOUIS C. A study of groundwater flow in jointed rock and its influence on the stability of rock masses[D]. London: Imperial College, 1969: 120−125.

[7] 赵阳升. 矿山岩石流体力学[M]. 北京: 煤炭工业出版社, 1994: 112−124. ZHAO Yangsheng. Rock fluid mechanics in mine[M]. Beijing: China Coal Industry Publishing House, 1994: 112−124.

[8] 叶源新, 刘光廷. 三维应力作用下砂砾岩孔隙型渗流[J]. 清华大学学报(自然科学版), 2007, 47(3): 335−339. YE Yuanxin, LIU Guangting. Porous seepage in calcirudite rock with 3-D stresses[J]. Journal of Tsinghua University (Science & Technology), 2007, 47(3): 335−339.

[9] 赵延林, 曹平, 汪亦显, 等. 裂隙岩体渗流−损伤−断裂耦合模型及应用[J]. 岩石力学与工程学报, 2008, 27(8): 1634−1643. ZHAO Yanlin, CAO Ping, WANG Yixian, et al. Coupling model of seepage- damage- fracture in fractured rock masses and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1634−1643.

[10] ZHAO Y L, TANG J Z, CHEN Y, et al. Hydromechanical coupling tests for mechanical and permeability characteristics of fractured limestone in complete stress–strain process[J]. Environmental Earth Sciences, 2017, 76(1): 24−42.

[11] 赵延林. 裂隙岩体渗流−损伤−断裂耦合理论与应用研究[D]. 长沙: 中南大学资源与安全工程学院, 2009: 77−118. ZHAO Yanlin. Coupling theory of seepage-damage fracture in fractured rock masses and its application[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2009: 77−118.

[12] 杨永明, 鞠杨, 刘红彬, 等. 孔隙结构特征及其对岩石力学性能的影响[J]. 岩石力学与工程学报, 2009, 28(10): 2031−2038. YANG Yongming, JU Yang, LIU Hongbin, et al. Influence of porous structure properties on mechanical Performances of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10): 2031−2038.

[13] LOCK P A, JING X D, ZIMMERMAN R W, et al. Predicting the permeability of sandstone from image analysis of pore structure[J]. Journal of Applied Physics, 2002, 92(10): 6311−6319.

[14] OKABE H, BLUNT M J. Prediction of permeability for porous media reconstructed using multiple-point statistics[J]. Physical Review E, 2004, 70(6): 1−10.

[15] 王金波, 黄耀辉, 鞠杨, 等.基于三维重构模型的孔隙岩石气体渗流的LBM模拟[J]. 煤炭工程, 2014, 46(5): 77−80.WANG Jinbo, HUANG Yaohui, JU Yang, et al. LBM simulation on gas seepage of porous rock based on 3D reconstructed model[J]. Coal Engineering, 2014, 46(5): 77−80.

[16] 仵彦卿, 曹广祝, 丁卫华. 砂岩渗透参数随渗透水压力变化的CT试验[J]. 岩土工程学报, 2005, 27(7): 780−785. WU Yanqing, CAO Guangzhu, DING Weihua. Permeability experiment of sandstone under variable seepage pressures by using X-ray CT real-time observation[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(7): 780−785.

[17] ANSELMETTI F S, LUTHI S, EBERLI G P. Quantitative analysis of carbonate rock pore system described by digital image[J]. AAPG Bulletin, 1998, 82(10): 1815−1836.

[18] HEILAND J, RAAB S. Experimental investigation of the influence of differential stress on permeability of a lower permian sandstone deformed in the brittle deformation field[J]. Phys Chem Earth(A), 2001, 26(1): 33−38.

[19] 王亮, 马宗武, 毛小虎. 圆柱体轴向点荷载加载破坏机理[J]. 矿业工程研究, 2015, 30(1): 69−75. WANG Liang, MA Zongwu, MAO Xiaohu. Research on failure mechanism of cylinder axial load[J]. Mining Engineering Research, 2015, 30(1): 69−75.

(编辑 杨幼平)

3-dimensional reconstruction model of rock with random pore structure and microscopic seepage analysis

ZHAO Yanlin1, 2, CAO Ping3, TANG Jinzhou1, MA Wenhao1, LI Shuqing1, WANG Wenjun1

(1. Work Safety Key Laboratory on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines, Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China;2. State Key Laboratory of Coal Resources and Safety Mining, China University of Mining and Technology, Xuzhou 221008, China;3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Taking porous rock medium as random microscopic structure with range of millimeters, rock model with 3-dimensional random pores was reconstructed, and the influence of pore structure to porous rock seepage was studied on the level of meso mechanics. By introducing microtubule seepage model, statistics principle and FLAC3Dsoftware were used to develop the reconstruction technology of porous rock medium with random pore structure produced and numerical simulation method of meso seepage. The results show that the time from unsteady flow to steady flow is shortened with the increase of porosity. There exists high accuracy linear relationship between seepage parameters andporosity, and the porosity threshold (n) of permeability of porous rock medium is 4.05%. The permeability of porous rock medium is mainly effected by volumetric stress. Furthermore, during pre–peak process the negative exponential relationship between the permeability and the volumetric stress is also shown. The numerical simulation stability of porous structure unit with range of millimeters can be guaranteed.

rock mechanics; pore structure; meso-scopic seepage; fluid-solid coupling; reconstruction model

10.11817/j.issn.1672-7207.2017.01.024

TU45

A

1672−7207(2017)01−0168−09

2016−01−03；

2016−03−16

国家自然科学基金资助项目(51274097，51434006，51374104)；湖南省自然科学基金资助项目(2015JJ2067)；中国矿业大学煤炭资源与安全开采国家重点实验室开放研究基金资助项目(SKLCRSM16KF12) (Projects(51274097, 51434006, 51374104) supported by the National Natural Science Foundation of China; Project(2015JJ2067) supported by the Natural Science Foundation of Hunan Province; Project(SKLCRSM16KF12) supported by the Open Projects of State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology)

赵延林，博士，教授，从事岩体渗流力学研究；E-mail: yanlin_8@163.com