环境激励下基础隔震结构时变模态频率的温度效应

郑文智 王 浩 杜永峰 茅建校

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)(2兰州理工大学防震减灾研究所, 兰州 730050)

环境激励下基础隔震结构时变模态频率的温度效应

郑文智1王 浩1杜永峰2茅建校1

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)(2兰州理工大学防震减灾研究所, 兰州 730050)

基于实测隔震层温度和结构加速度响应数据,分析了环境温度对基础隔震结构模态频率的影响规律.首先,采用小波变换方法识别了基础隔震结构时变模态频率;然后,分别采用单自由度简化模型和双自由度简化模型推导了环境温度对基础隔震结构模态频率的影响机理,对基础隔震结构模态频率与隔震层温度进行了相关性分析,提出温度对模态频率的影响系数,量化了隔震层温度对隔震结构模态频率的影响,并结合隔震支座温度相关性试验,对相关性分析结果进行了验证;最后,通过参数回归分析,提出模态频率与温度的相关性模型,并给出了温度对基础隔震结构模态频率的影响系数曲线.结果表明,实测温度影响系数曲线与隔震支座温度相关性试验结果表现出较好的一致性,可为基础隔震结构的性能评估提供可靠依据.

基础隔震结构;结构健康监测;小波变换;时变模态频率;温度效应

Abstract: Based on measured temperature and structural acceleration response of a base-isolated structure (BIS), the influence of the ambient temperature on the modal frequency of the BIS is analyzed. First, the wavelet transform method is used to identify the time-varying modal frequency of the BIS. Then, the influence mechanism of the ambient temperature on the modal frequency of the BIS is deduced by using the singular degree of freedom simplified model and the two degree of freedom simplified model, respectively. The correlation analysis between the modal frequency and the temperature of the BIS is investigated. The influence of the temperature on the modal frequency is quantitatively by the proposed influence coefficients. The correlation analysis results are verified by the temperature correlation test of isolation bearings. Finally, the correlation models of the modal frequency with the temperature are presented. The influence coefficient curves of the temperature on the modal frequency are obtained. The results show that the measured influence coefficient curves agree well with the correlation test results, which can provide reliable basis for performance of BISs.

Keywords: base-isolated structure; structural health monitoring; wavelet transform; time-varying modal frequency; temperature effect

在长期环境荷载作用下,隔震结构的自身特性会发生变化,环境温度会对结构的动力特性产生周期性的影响[1-2].地震等突发荷载作用对隔震结构引起的损伤是不可逆的,探究环境温度作用下隔震结构模态参数的演变规律,基于监测数据,建立客观、定量的数值模型,精确描述环境温度对隔震结构模态参数的影响程度,消除环境因素的影响,可准确地评估地震等突发荷载作用而引起的损伤程度,是准确、合理评估隔震结构震后结构性能的依据[3-4].模态参数是描述基础隔震结构动力特性发生变化的依据,准确识别结构的模态参数至关重要.相比随机子空间法(SSI)、自然激励法(NExT)、希尔伯特-黄变换(HHT)等环境激励下的模态参数识别方法,小波变换因其在时-频域都具有表征信号局部特征的能力,以其较高的识别精度与抗噪能力,在结构模态参数识别中得到了广泛的应用[5-7].Kijewski等[5]通过对称延拓,有效抑制了小波变换方法的边端效应;滕军等[7]提出了基于最小标准差的小波中心频率及带宽的自适应选择方法,提高了密集模态的识别精度.与此同时,国内外学者针对隔震支座在不同温度条件下的力学性能进行了试验研究[8-10].刘文光等[8]、李黎等[9]对不同直径的铅芯橡胶隔震支座在不同温度条件下的力学性能进行了试验研究,给出了隔震支座屈服前刚度、等效刚度的修正公式.众多学者探究了桥梁结构模态参数的温度效应[11-13],而隔震结构模态参数的温度效应鲜有研究[14-15].规范关于环境温度对隔震结构的影响尚有空缺[16].为研究环境温度对隔震结构模态频率的影响,基于某基础隔震结构长期监测的隔震层温度、加速度数据[2],采用小波变换方法识别隔震结构的模态频率,研究了环境温度作用下隔震结构模态频率的演变机理,提出了温度相关性模型及温度影响系数曲线,量化分析了环境温度对基础隔震结构模态频率的影响,并结合隔震支座温度相关性试验进行了验证.

1 基于小波的隔震结构模态参数识别

1.1 小波变换的模态参数识别原理

连续的小波变换系数可定义为

(1)

n自由度系统的自由衰减振动信号为

(2)

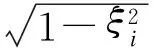
对任意一阶模态频率fi而言,n自由度系统的自由衰减振动信号对应的小波变换系数为

(3)

式中,ai为第i阶模态频率fi对应的尺度参数.则系统的第i阶模态频率fi及模态阻尼比ξi可由下式求得:

(4a)

arg[Wψ(ai,b)]=2πfib+ψ0i

(4b)

小波变换的时频分辨率取决于母小波ψ(t)及相关参数[5],Complex-Morlet小波的时域可描述为

(5)

式中,fb为带宽参数;fc为小波中心频率;为得到最佳频率分辨率并去除边端效应,调整fb,fc使其满足

(6)

式中,Δfi,i+1=fi+1-fi;fi,i+1=(fi+1+fi)/2;Td为待分析信号的长度;α,β,γ为相关参数,当α=2,β=4,γ=0.4时,可充分消除边端效应[17].

1.2 基础隔震结构模态频率识别

基于文献[2]中实测基础隔震结构加速度响应数据与温度数据,数据采集时间为2013-01,2014-01和2014-08,测试环境平均温度分别为-6.6,-1.3,22.8 ℃,每次数据采集时间为30 min.限于篇幅,只列出部分原始数据.2013-01纵向加速度时程曲线如图1所示.对实测加速度信号

图1 2013-01纵向加速度时程曲线

进行连续小波变换,依据式(6)确定相关参数,fb,fc的最优值分别为16和8 Hz,其时频分布见图2.基于模极大值理论提取了小波系数的小波脊曲线,得到基础隔震结构一阶纵向、一阶横向及二阶瞬时模态频率(见图3).该结构的一阶横向、一阶纵向及二阶模态振型如图4所示.

(a) 一阶横向频率

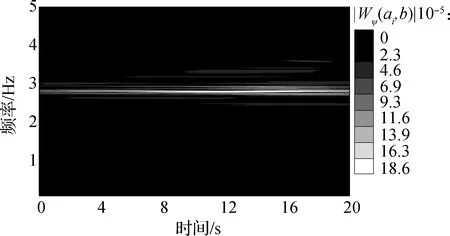
(b) 一阶纵向频率

(c) 二阶频率

2 隔震结构模态频率-温度相关性分析

2.1 隔震支座-温度相关性试验

铅芯橡胶隔震支座的弹性模量、泊松比、性能与单一的叠层橡胶或铅芯大不相同.在环境温差较大的部分地区,低温环境对隔震支座的力学性能有明显影响,冬季极端低温对隔震支座力学性能的影响不可忽略.根据建筑用铅芯橡胶隔震支座温度相关性试验结果[9-10],当环境温度T∈(-40,40) ℃时,温度对隔震支座屈服前刚度、等效刚度(剪应变为100%)的影响系数如图5所示.

(a) 一阶横向频率

(b) 一阶纵向频率

(c) 二阶频率

(a) 一阶横向模态振型

(b) 一阶纵向模态振型

(c) 二阶模态振型

2.2 温度对隔震结构模态频率的影响机理分析

环境温度会对结构动力特性产生较大影响[3-4].由于隔震支座对上部结构的侧向约束较弱,在施工期和服役初期,环境温度引起的上部结构水平变形[15]可通过隔震支座产生水平位移得以释放,使环境温度作用引起的应力释放,而环境温度变化会引起隔震支座材料弹性模量产生改变,导致隔震支座刚度发生变化,从而引起隔震结构模态频率的改变.

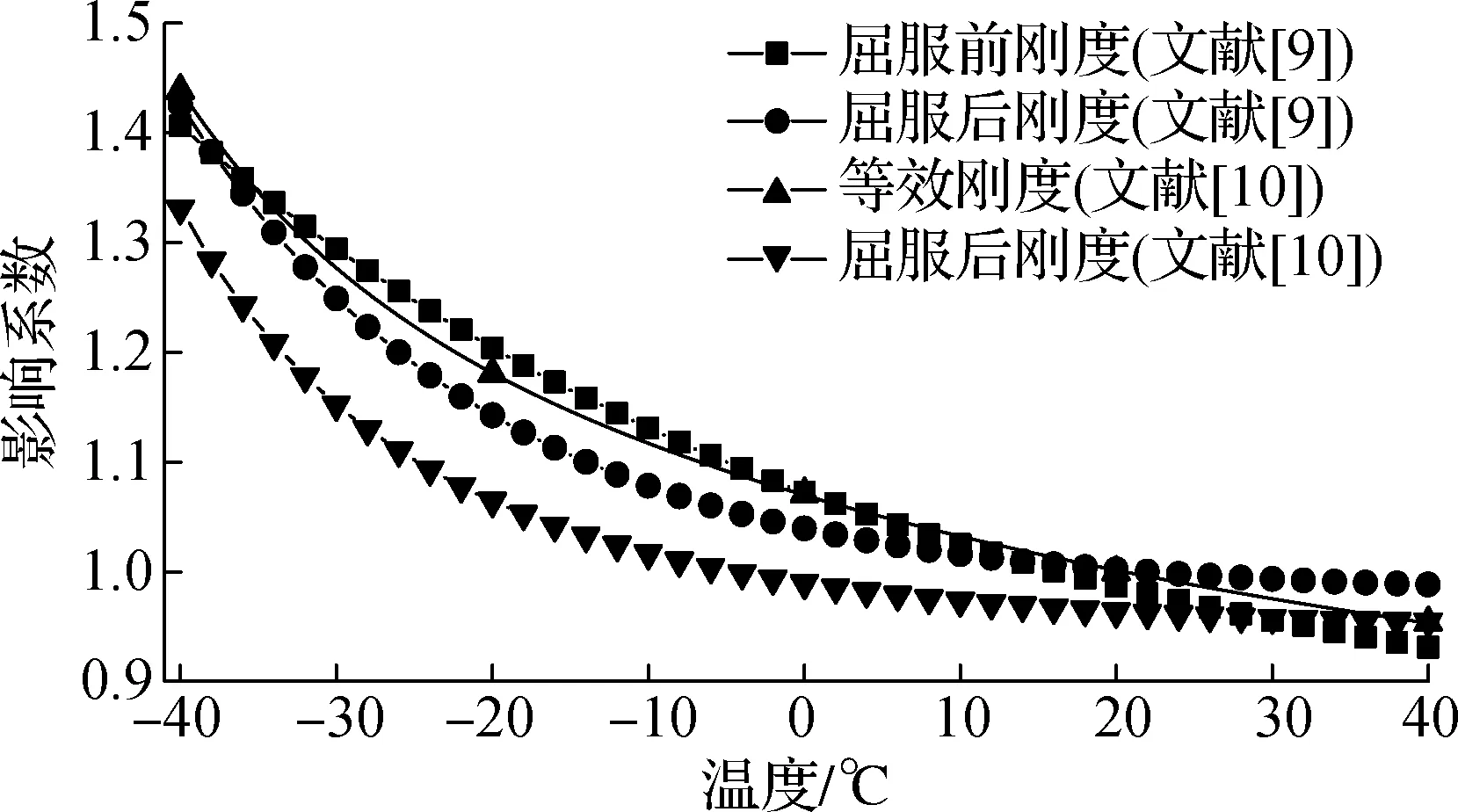
图5 温度对隔震支座刚度的影响系数

存储成本又称持有成本，是企业在一段时间内存储或是持有商品而产生的，一般与企业所持有的平均库存量成正比。

2.2.1 单自由度简化模型

脉动(微振)情况下,结构阻尼比较小,为1%～3%,此时,阻尼对结构模态频率的影响可忽略不计[18].单自由度体系无阻尼自由振动方程为

(7)

由式(7)可得出体系的频率方程为

(8)

由式(8)可得到基础隔震结构自振频率为

(9)

环境温度作用下,铅芯橡胶隔震支座刚度受温度影响程度可定量表述为

(10)

基于隔震支座温度相关性试验,可将温度对支座刚度的影响系数表述为

Rk=c+de-λT

(11)

则结构的自振频率可表述为

(12)

进一步可将式(12)表示为

(13)

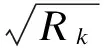
2.2.2 双自由度简化模型

对于层数不太高的隔震房屋,上部结构的弯曲变形和倾覆力矩通常都可忽略,可以简化为隔震系统和上部结构的等效单质点系统串联而成的双自由度剪切型结构[19].双自由度体系的无阻尼振动方程为

(14)

式(14)有非零解,即

(15)

由式(15)得结构的二阶模态频率为

(16)

ω20=

(17)

由式(17)可定义环境温度对隔震结构二阶频率的影响系数为

(18)

任意环境温度条件下,基础隔震结构的模态频率为

(19)

2.3 模态频率-温度相关性分析

(20a)

(20b)

(20c)

式中,Rc为相关性系数.

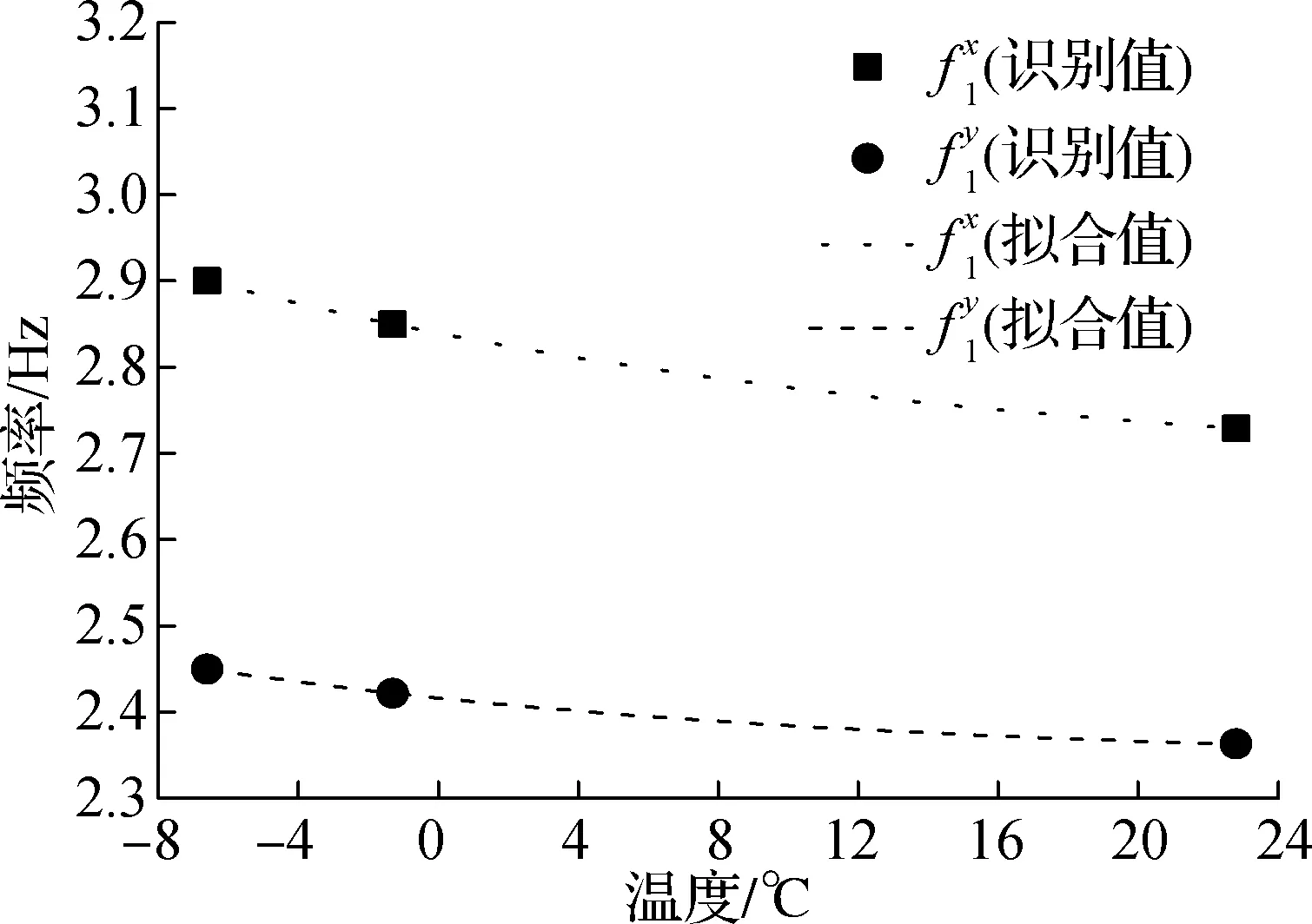
(a) 一阶频率

(b) 二阶频率

(21a)

(21b)

Rf2=0.999 47+0.002 58e-0.08T

(21c)

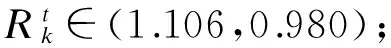
(a) 一阶频率

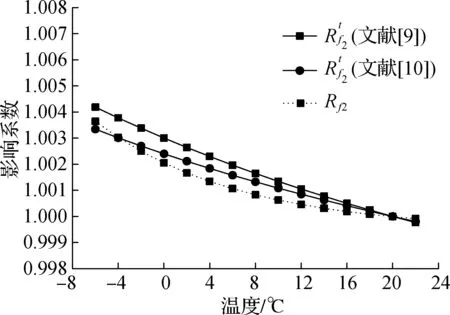
(b) 二阶频率

由图7可知,实测环境温度对结构一阶频率、二阶频率的影响系数与文献[9-10]的试验结果趋势吻合较好.由实测结果可以看出,环境温度对基础隔震结构自振频率有一定影响,但对基础隔震结构高阶频率的影响较小.存在偏差的原因主要在于:① 铅芯橡胶隔震支座温度相关性试验结果直接依赖于支座直径、数量、试验条件,尤其与试验中温度环境的控制密切相关;② 引起隔震结构模态频率发生变化的环境因素包括风荷载、湿度、温度等,需进行更加深入的研究.

3 结论

1) 环境激励下,短时间内基础隔震结构的模态频率基本不变,其模态频率在某一特定值附近上下波动,但波动范围较小.

2)T∈(-6,22) ℃时,环境温度对基础隔震结构的自振频率有一定影响,环境温度越低,影响越大;对基础隔震结构高阶频率的影响很小,可以忽略不计.

3) 通过频率影响系数量化分析环境温度对模态频率的影响,实测分析结果与隔震支座温度相关性试验结果趋势吻合较好.基于识别的时变模态频率建立温度相关性模型,为消除环境温度的影响,合理评估隔震结构性能提供可靠依据.

4) 环境温度是影响基础隔震结构模态频率的主要因素,同时也受到其他因素的影响.对于实际工程问题,需依据实际工程所在地区的环境特点,对众多影响因素(如地震、强风等突发荷载,温度、湿度等)同时进行分析,综合分析主要影响因素.温度相关性模型仍需基于长期监测数据进行修正,准确分离环境温度引起的基础隔震结构模态频率变化与损伤引起的模态频率变化,为准确评估基础隔震结构性能提供依据.

References)

[1] 李万润,郑文智,杜永峰,等.基础隔震结构健康监测系统的设计与实现(Ⅰ):系统设计[J].地震工程学报,2016,38(1):94-102. DOI:10.3969/j.issn.1000-0844.2016.01.0094. Li Wanrun, Zheng Wenzhi, Du Yongfeng, et al. Design and implementation of structural health monitoring system for base-isolated structure (Ⅰ): System design[J].ChinaEarthquakeEngineeringJournal, 2016,38(1): 94-102. DOI:10.3969/j.issn.1000-0844.2016.01.0094.(in Chinese)

[2] 杜永峰,郑文智,李万润,等.基础隔震结构健康监测系统的设计与实现(Ⅱ):系统实现[J].地震工程学报,2016,38(3):344-352. DOI:10.3969/j.issn.1000-0844.2016.03.0344. Du Yongfeng, Zheng Wenzhi, Li Wanrun, et al. Design and implementation of health monitoring system for base-isolated structure (Ⅱ): System implementation[J].ChinaEarthquakeEngineeringJournal, 2016,38(3): 344-352. DOI:10.3969/j.issn.1000-0844.2016.03.0344.(in Chinese)

[3] 闵志华,孙利民,淡丹辉.影响斜拉桥模态参数变化的环境因素分析[J].振动与冲击,2009,28(10):99-105. DOI:10.3969/j.issn.1000-3835.2009.10.020. Min Zhihua, Sun Limin, Dan Danhui. Effect analysis of environmental factors on structural modal parameters of a cable-stayed bridge[J].JournalofVibrationandShock, 2009,28(10): 99-105. DOI:10.3969/j.issn.1000-3835.2009.10.020.(in Chinese)

[4] 邓扬,李爱群,刘扬,等.基于监测数据的大跨度悬索桥频率与环境条件的相关性模型[J].中南大学学报(自然科学版),2014,45(7):2401-2409. Deng Yang, Li Aiqun, Liu Yang, et al. Correlation models of modal frequencies and environmental conditions for a long-span suspension bridge based on monitoring data[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2014,45(7): 2401-2409.(in Chinese)

[5] Kijewski T, Kareem A. Wavelet transforms for system identification in civil engineering[J].Computer-AidedCivilandInfrastructureEngineering, 2003,18(5): 339-355. DOI:10.1111/1467-8667.t01-1-00312.

[6] Lardies J, Ta M N, Berthillier M. Modal parameter estimation based on the wavelet transform of output data[J].ArchiveofAppliedMechanics(IngenieurArchiv), 2004,73(9): 718-733. DOI:10.1007/s00419-004-0329-6.

[7] 滕军,朱焰煌,周峰,等.基于复Morlet小波变换的大跨空间结构模态参数识别研究[J].振动与冲击,2009,28(8):25-29. DOI:10.3969/j.issn.1000-3835.2009.08.006. Teng Jun, Zhu Yanhuang, Zhou Feng, et al. Modal parameters identification of large-span spatial structures based on complex Morlet wavelet transform[J].JournalofVibrationandShock, 2009,28(8): 25-29. DOI:10.3969/j.issn.1000-3835.2009.08.006.(in Chinese)

[8] 刘文光,杨巧荣,周福霖.建筑用铅芯橡胶隔震支座温度性能研究[J].世界地震工程,2003,19(2):39-44. DOI:10.3969/j.issn.1007-6069.2003.02.007. Liu Wenguang, Yang Qiaorong, Zhou Fulin. Temperature properties of lead rubber bearings for building[J].WorldEarthquakeEngineering, 2003,19(2): 39-44. DOI:10.3969/j.issn.1007-6069.2003.02.007.(in Chinese)

[9] 李黎,叶昆,江宜城.橡胶铅芯隔震支座力学性能的温度效应研究[J].华中科技大学学报(城市科学版),2009,26(3):1-3. DOI:10.3969/j.issn.2095-0985.2009.03.001. Li Li, Ye Kun, Jiang Yicheng. Thermal effect on the mechanical behavior of lead-rubber bearing[J].JournalofHuazhongUniversityofScienceandTechnology(UrbanScienceEdition), 2009,26(3): 1-3. DOI:10.3969/j.issn.2095-0985.2009.03.001.(in Chinese)

[10] 刘文光,秦皇婷,何文福,等.极低温度下LRB力学性能及对高层结构地震响应的影响[J].振动与冲击,2012,31(13):85-90. DOI:10.3969/j.issn.1000-3835.2012.13.018. Liu Wenguang, Qin Huangting, He Wenfu, et al. Mechanical properties of LRB in low temperature state and its influence on earthquake response of high buildings[J].JournalofVibrationandShock, 2012,31(13): 85-90. DOI:10.3969/j.issn.1000-3835.2012.13.018.(in Chinese)

[11] Ding Y L, Li A Q, Liu T. Environmental variability study on the measured responses of Runyang Cable-stayed Bridge using wavelet packet analysis[J].ScienceinChinaSeriesE:TechnologicalSciences, 2008,51(5): 517-528.DOI:10.1007/s11431-008-0043-7.

[12] Li H, Li S L, Ou J P, et al. Modal identification of bridges under varying environmental conditions: Temperature and wind effects[J].StructuralControlandHealthMonitoring, 2010,17(5): 495-512. DOI:10.1002/stc.319.

[13] Mosavi A A, Seracino R, Rizkalla S. Effect of temperature on daily modal variability of a steel-concrete composite bridge[J].JournalofBridgeEngineering, 2012,17(6): 979-983. DOI:10.1061/(asce)be.1943-5592.0000372.

[14] 朱文正,张季超.基于智能传感技术的广东科学中心隔震系统实时监测研究[J].土木工程学报,2014,47(5):40-45. DOI:10.15951/j.tmgcxb.2014.05.013. Zhu Wenzheng, Zhang Jichao. Real time monitoring of isolation system of Guangdong Science Center based on intelligent sensor technology[J].ChinaCivilEngineeringJournal, 2014,47(5): 40-45. DOI:10.15951/j.tmgcxb.2014.05.013.(in Chinese)

[15] 杜永峰,郑文智,李万润,等.超长复杂基础隔震结构静动力特性温度相关性研究[J].工程力学,2017,34(7):69-78. Du Yongfeng, Zheng Wenzhi, Li Wanrun, et al. Study on the dependency of static and dynamic characteristics with environmental temperature for long irregular base-isolated structures[J].EngineeringMechanics, 2017,34(7): 69-78. (in Chinese)

[16] 中华人民共和国住房和城乡建设部.GB50011—2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.

[17] Yan B, Miyamoto A. A comparative study of modal parameter identification based on wavelet and Hilbert-Huang transforms[J].Computer-AidedCivilandInfrastructureEngineering, 2006,21(1): 9-23. DOI:10.1111/j.1467-8667.2005.00413.x.

[18] 刘晶波,杜修力.结构动力学[M].北京:机械工业出版社,2005:38-39.

[19] 李中锡,周锡元.规则型隔震房屋的自振特性和地震反应分析方法[J].地震工程与工程振动,2002,22(2):33-41. DOI:10.13197/j.eeev.2002.02.006. Li Zhongxi, Zhou Xiyuan. Simplified analysis method of seismically isolated regular building[J].EarthquakeEngineeringandEngineeringVibration, 2002,22(2): 33-41. DOI:10.13197/j.eeev.2002.02.006. (in Chinese)

Temperatureeffectoftime-varyingmodalfrequencyofbase-isolatedstructureunderambientexcitation

Zheng Wenzhi1Wang Hao1Du Yongfeng2Mao Jianxiao1

(1Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China) (2Institute of Earthquake Protection and Disaster Mitigation, Lanzhou University of Technology, Lanzhou 730050, China)

TU352.12

A

1001-0505(2017)05-0999-07

10.3969/j.issn.1001-0505.2017.05.025

2016-11-25.

郑文智(1992—),男,博士生；王浩(联系人),男,博士,研究员,博士生导师,wanghao1980@seu.edu.com.

国家重点基础研究发展计划(973计划)青年科学家专题资助项目(2015CB060000)、国家自然科学基金资助项目(51578151，51438002)、中央高校基本科研业务费专项资金资助项目(2242015K42028).

郑文智,王浩,杜永峰,等.环境激励下基础隔震结构时变模态频率的温度效应[J].东南大学学报(自然科学版),2017,47(5):999-1005.

10.3969/j.issn.1001-0505.2017.05.025.