单调荷载下钢材延性断裂损伤因子模型及参数校准

李灿军 周 臻 朱亚智 卢 璐

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)(2德州大学奥斯汀分校土木建筑和环境工程系, 奥斯汀 78703)(3国网江苏省电力公司经济技术研究院, 南京 210008)

单调荷载下钢材延性断裂损伤因子模型及参数校准

李灿军1周 臻1朱亚智2卢 璐3

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)(2德州大学奥斯汀分校土木建筑和环境工程系, 奥斯汀 78703)(3国网江苏省电力公司经济技术研究院, 南京 210008)

为提高钢材断裂模型的通用性和实时性,采用延性损伤因子概念,分别建立了基于VGM的VGM-DDF断裂模型和基于Johnson-Cook的JC-DDF断裂模型．结合不同槽口半径光滑圆棒试件的单向拉伸试验和有限元分析,研究了不同试件加载过程中应力三轴度和等效塑性应变的关系,并对国产Q235钢在单调荷载下延性断裂损伤因子模型参数进行了校准．采用校准后的断裂模型计算了各试件断裂损伤因子值,利用Abaqus软件对钢材断裂进行全过程模拟,并对不同的单元网格尺寸模型进行分析．结果表明:损伤因子模型的有效性得到验证,且JC-DDF模型离散性更小;断裂后荷载位移模拟曲线与试验曲线具有较好的吻合度;有限元单元网格尺寸影响断裂预测精度,并建议网格尺寸取0.25 mm．

Q235钢;延性断裂;损伤因子模型;单向拉伸试验;参数校准

Abstract: To promote the applicability and the instantaneity of the steel fracture model, by adopting the concept of the ductile damage factor, the VGM-DDF and JC-DDF fracture predicted models were established based on the void growth model(VGM) and the Johnson-Cook model, respectively. Combining the monotonic tensile test of smooth bars with different notch radii and finite element analyses, the relationship between the stress triaxiality and the equivalent plastic strain during the loading process of various bars was studied, and the ductile fracture damage factor model parameters for China Q235 steels under monotonic tension were calibrated. The ductile damage factor of each component was calculated by using the calibrated models. The whole fracture process of steel was simulated by Abaqus software, and the models with different element mesh sizes were analyzed. The results show that the effectiveness of the ductile damage factor models was validated, and the discreteness of the JC-DDF model is smaller. The predicted displacement-load curves after fracture agree well with the test results. The finite element mesh size affects the fracture prediction accuracy, and the size is suggested to be 0.25 mm.

Keywords: Q235 steel; ductile fracture; damage factor model; monotonic tension test; parameter calibration

在传统抗震设计理念中,钢结构通常被认为具有足够的延性,且主要依靠局部或整体构件的塑性变形来实现[1-2]．但在1994年北岭地震和1995年日本神户地震中出现了大量钢材断裂现象,广大学者开始对钢结构延性断裂展开研究[2-3]．

目前,普遍认为钢材延性断裂与材料微空隙的增长机制有关,材料微观空穴的形核、增长、联合是材料出现延性断裂的主要原因[4]．众多学者基于应力三轴度和等效塑性应变等参数,建立了钢材延性断裂模型．文献[5-6]分别提出了适用于单调荷载下的VGM模型和SMCS模型,文献[7]通过试验和模拟分析验证了这2个模型的有效性．文献[8]提出了适用于常应变率和常温下的Johnson-Cook断裂模型,且模型通用性较强．基于Miner原则,Jia等[9]在VGM模型中引入损伤因子概念,预测了软钢在单向荷载下的延性断裂．

钢材断裂与材料特性等因素相关,不同型号钢材的断裂参数应分别校准．文献[10-12]分别对国产Q345,Q460钢断裂参数进行了较为系统的研究．本文以国产Q235钢为例,引入延性损伤因子,分别建立了基于VGM的VGM-DDF断裂模型和基于Johnson-Cook的JC-DDF断裂模型,并结合试验和有限元模拟,对国产Q235钢的VGM-DDF和JC-DDF断裂模型参数进行了校准．采用校准后的模型模拟钢材断裂全过程,并讨论了有限元模型单元网格尺寸对预测断裂的影响．

1 延性损伤因子模型的通用表达

从损伤的角度来看,延性断裂可认为是损伤累积所致．由于钢材延性断裂机制以等效塑性应变达到临界断裂应变为判定准则,为定量描述材料损伤的累积过程,引入了与塑性应变增量相关的损伤因子增量(dD),其计算式为

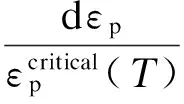
(1)

(2)

式中,σm和σe分别为静水应力和有效应力．

根据线性累计损伤理论[9],累积每一加载步产生的损伤因子增量,则定义总损伤因子D达到1时,材料产生破坏．因此,损伤模型通用表达式为

(3)

在较小的增量步内,认为应力三轴度值不变,但对于不同的增量步,应力三轴度值不同．因此,损伤因子模型考虑了应力三轴度在加载过程中的变化,能更准确地描述每一加载时刻的累积损伤值．

2 不同断裂模型下的损伤因子模型

2.1VGM-DDF模型

根据VGM模型[7],材料达到断裂点时满足

(4)

式中,η为与材料相关的断裂常数．

结合式(3)和(4),VGM-DDF模型可表示为

(5)

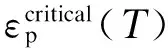
2.2JC-DDF模型

根据Johnson-Cook模型[8],不考虑温度和应变率的影响,材料达到断裂点时满足

(6)

式中,C1,C2,C3为断裂相关的材料参数,可由材料试验校准．

JC-DDF模型可表示为

(7)

式(7)为积分形式,利用试验数据直接校准3个参数C1,C2和C3存在很大困难．本文采取如下步骤对参数进行校准:

① 利用试验断裂应变和应力三轴度数据,对式(6)进行非线性回归,初步校准参数C1,C2和C3．由于式(6)不考虑加载过程中应力三轴度的变化,损伤因子模型的校准存在误差．后续固定C1,C2为初步校准值,对C3进行二次校准,以满足精度要求．初步校准时平均应力三轴度计算式为

(8)

式中,Ti为增量步i的应力三轴度;Δεpi为等效塑性应变增量．

② 令C2为原始校准值,利用式(7),结合加载全过程应力应变数据,计算试件断裂时刻的损伤因子D．

③ 将断裂时刻的损伤因子D与1进行比较,若D>1则调大C2,若D<1则调小C2,然后重新计算断裂时刻的损伤因子D．如此循环,直到断裂时刻D=1,此时的C2即为试件二次校准的参数值．

3 单向拉伸试验及有限元模拟

3.1 试验方案

将同一批Q235B钢材分别加工成光滑圆棒和平滑槽口试件．光滑圆棒试件3根,记为A1～A3;平滑槽口试件按照不同槽口半径(r=1.500,3.125,6.250 mm)各加工2根,分别记为A4～A5,A12～A13,A20～A21．试件设计尺寸如图1所示．试验加载装置为50 t MTS液压伺服材料试验机,引伸计标距分别为50和25 mm．试验按位移加载,试件和引伸计如图2所示．

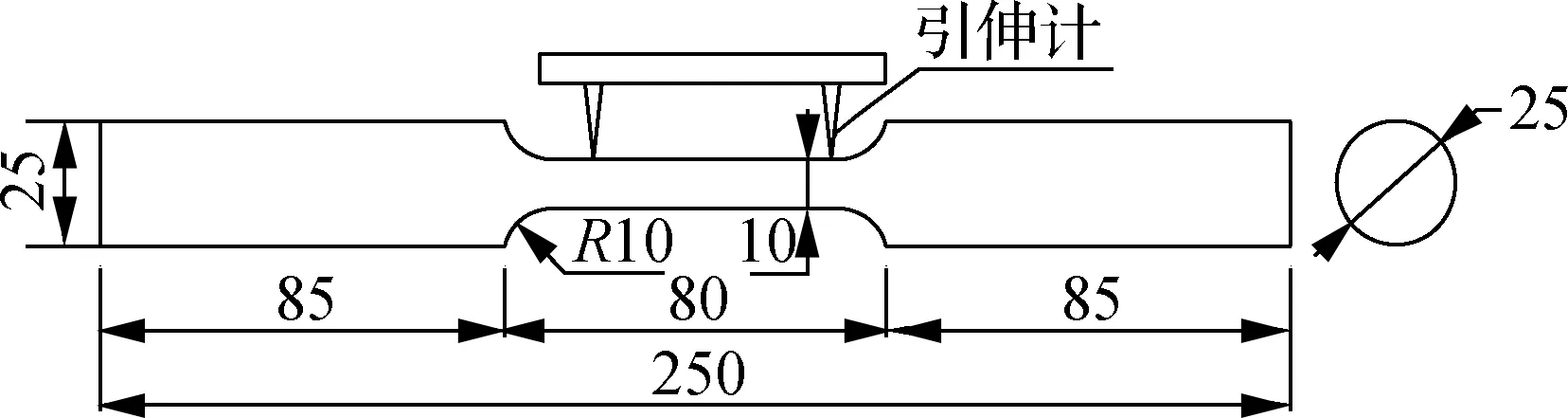
(a) 光滑圆棒

(b) 平滑槽口试件(r=3.125 mm)

图2 试件与引伸计

光滑圆棒单向拉伸试验结果可用于材料本构参数的测定．同时,由于光滑圆棒试件与断裂试验中平滑槽口试件的应力应变状态不同,故此试验结果也可用于后续材料断裂模型参数的校准．

3.2 真实应力-塑性应变曲线的校准

试件颈缩前的真实应力-塑性应变关系基于如下2个假定[9]:① 构件颈缩前引伸计范围内应变沿构件长度方向是均匀的;② 构件颈缩前构件横截面上应力是均匀的．真实应力σtrue和真实应变εtrue分别为

(9)

(10)

式中,Ainitinal为试件初始截面面积;Linitinal为初始引伸计长度;P为某一时刻加载荷载;L为同时刻引伸计范围内试件长度;A为同时刻试件截面面积．

真实应变εtrue是由弹性应变εel和塑性应变εpl两部分组成的．塑性应变为

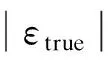
(11)

式中,E为钢材初始弹性模量．

当构件发生颈缩后,上述计算真实应力应变的公式不再适用．采用MWA方法[9]并根据材料荷载位移曲线校准材料颈缩后真实应力应变曲线．颈缩时刻材料的真实应力σneck和颈缩后材料的真实应力σtrue分别为

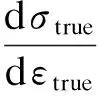
(12)

σtrue=σneck+ωσneck(εtrue-εneck) 0<ω<1

(13)

式中,ω为材料参数,经材料试验确定．

根据MWA方法,在有限元软件Abaqus中按位移控制模拟试验过程．由于试件A1的试验结果相比其他试件差异较大,故不作为有效试件．图3给出了不同ω值对应的荷载-位移模拟曲线和试验曲线．由图可知,当ω=0.977时,有限元模拟曲线和试验曲线吻合较好,由此可校准Q235圆棒真实应力-塑性应变曲线(见图4)．

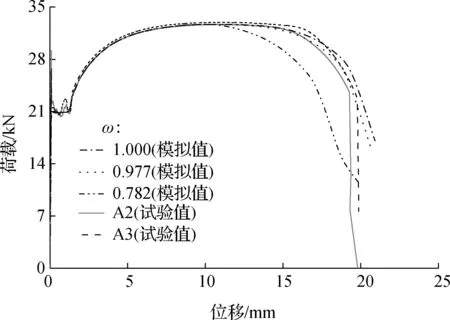
图3 不同ω值对应的荷载-位移曲线

3.3 单向拉伸试验的有限元模拟

鉴于试件形状和加载条件的对称性,利用有限

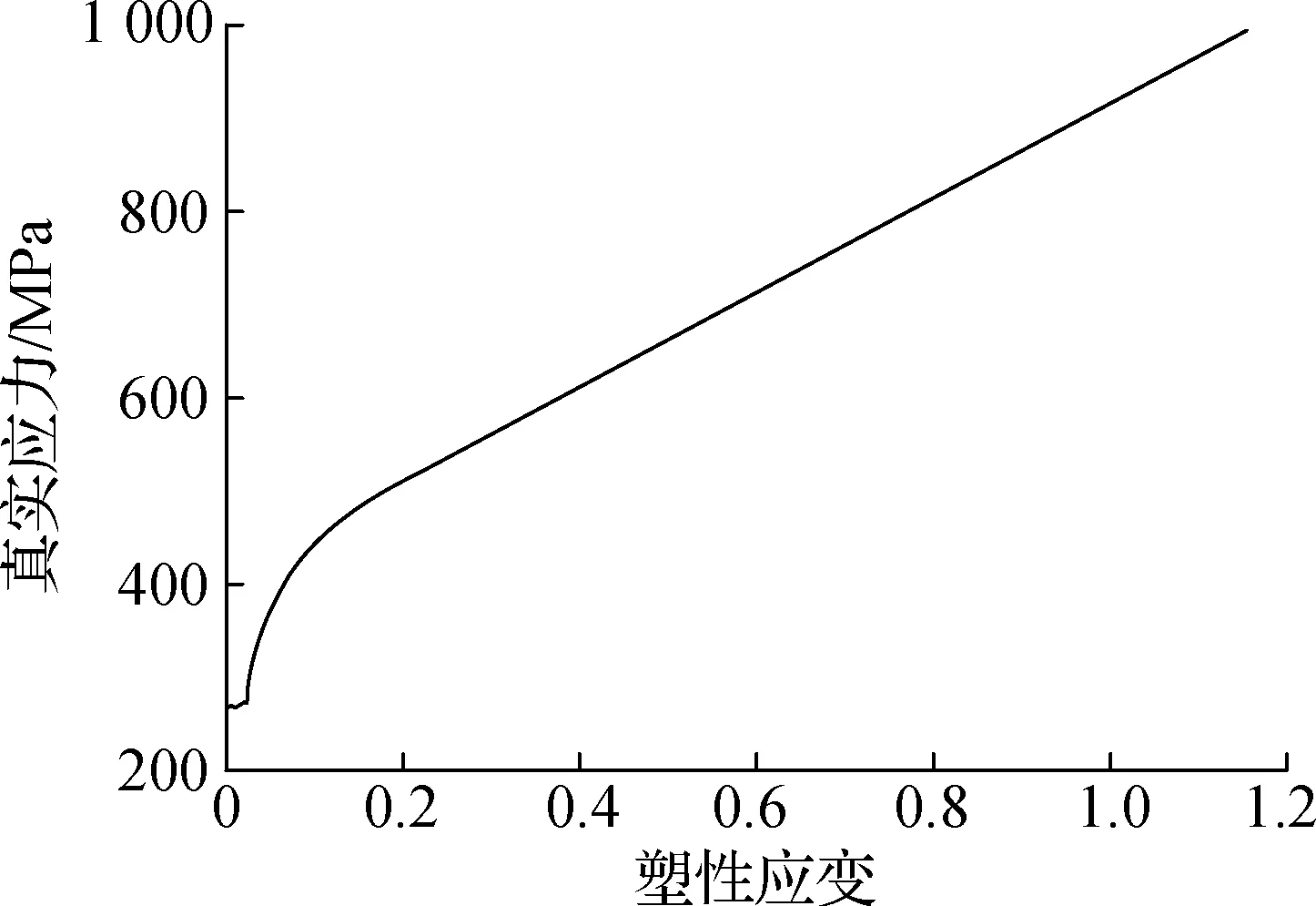
图4 校准的塑性应变-真实应力曲线

元软件Abaqus取构件的1/4进行建模分析,并采用C3D8R单元．引伸计范围内单元网格尺寸取0.25 mm,其余部分取2 mm．以r=3.125 mm为例,网格划分如图5所示．弹性模量取为208 GPa,泊松比取为0.3,塑性应变信息按3.2节校准的真实应力-塑性应变曲线输入．按位移加载,加载端与定义在位于中心轴上的参考点耦合,加载位移通过该参考点间接施加于构件,采用隐式静力分析．

(a) 1/4模型

4 延性损伤因子模型的参数校准

4.1 应力三轴度与等效塑性应变

为进一步分析应力三轴度与等效塑性应变的关系,从有限元软件中提取试件断裂部位的应力、应变信息．图6给出了不同槽口试件应力三轴度和等效塑性应变沿直径的变化趋势图．由图可知,试件槽口半径越大,应力三轴度越小,断裂等效塑性应变越大．即随着应力三轴度的减小,断裂等效塑性应变增大,这与延性断裂机制的理论分析一致．同时,从中心点到边点,应力三轴度明显减小,而等效塑性应变沿直径方向变化较小,因此认为断裂初始点为中心点．

加载过程中试件槽口截面中心点应力三轴度和等效塑性应变的关系如图7所示．由图可知,加载全过程试件的应力三轴度变化较大,尤其在等效塑性应变小于0.1的范围内,三轴度值出现跳跃现象,说明在预测材料断裂过程中应尽可能考虑应力三轴度的实时变化．

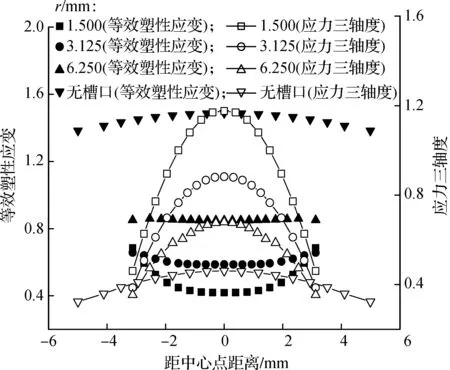
图6 应力三轴度和等效塑性应变变化图

图7 不同槽口试件应力三轴度与等效塑性应变关系

4.2VGM-DDF模型

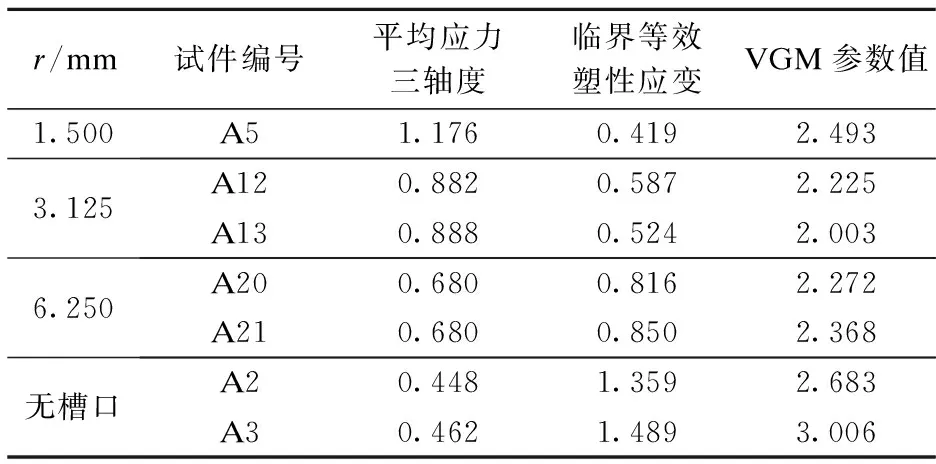
表1 Q235B钢VGM模型参数

取各试件VGM参数值的平均值(2.436)作为校准后的模型参数,则Q235B钢校准后的VGM-DDF断裂模型为

(14)

4.3JC-DDF模型

利用表1中的临界等效塑性应变与应力三轴度值,对式(6)进行非线性指数拟合,初步校准Johnson-Cook模型参数,得到C1=0.302,C2=5.102,C3=-3.344．

固定C1和C3,对C2进行二次校准,可得各试件JC-DDF模型中二次修正的参数．取C2的平均值5.196作为校准后的模型参数,得到Q235B钢校准后的JC-DDF断裂模型为

(15)

4.4 不同模型校准结果比较

用校准后的损伤因子模型确定各试件的损伤因子,结果见表2．由表可知,在进行二次校准JC-DDF断裂模型参数之前,损伤因子平均值为1.009,其误差来源于参数校准过程中未考虑应力三轴度的变化;而VGM-DDF断裂模型在形式上与VGM断裂模型等效,损伤因子平均值为1．为便于循环荷载下断裂模型校准,应尽可能提高损伤因子的校准精度．

表2 单向拉伸试件断裂时各损伤因子模型的损伤因子

为验证损伤因子模型的有效性,用校准后的模型计算各试件断裂时的损伤因子值．图8给出了不同模型计算的损伤因子值分布．由图可知,损伤因子计算值均分布在0.8～1.2之间,且大多数计算值与理论值相近,表明损伤因子模型具有一定的有效性．此外,JC-DDF模型得到的各试件损伤因子值波动性较小,究其原因在于模型参数较多,使模拟结果更接近试验结果,故JC-DDF模型具有较小的离散性．

图8 不同损伤因子模型各试件损伤因子值分布

5 断裂过程模拟及分析

5.1 断裂过程模拟

为得到试件断裂的全过程分析结果,以r=3.125 mm的试件为例,将校准后的JC-DDF模型参数输入Abaqus软件,并采用显示动力分析方法．图9给出了试件槽口断裂模拟形态与试验形态．图10为试件槽口断裂过程的有限元模拟结果．

(a) 模拟形态

(a) 位移1.65 mm

(c) 位移2.11 mm

由图9可知,试件断裂模拟形态与试验断裂形态吻合较好．由图10可知,随着加载位移的增加,试件颈缩区域单元从试件中心处至试件表面依次失效,与试验得到的裂缝由中间向外侧发展的结论相符合．模型中心点失效时位移为1.65 mm,随后失效点向外扩展,当位移为2.06 mm时试件完全断开．

5.2 单元网格尺寸的影响

在断裂模型参数的校准过程中,有限元单元尺寸对断裂失效点的判断及发展产生显著影响．对槽口区域采用3种网格分析,网格尺寸分别为0.15,0.25,0.40 mm．图11给出了相应的荷载-位移曲线．由图可知,网格尺寸为0.15和0.25 mm的模型断裂点时刻接近,加载位移分别为1.64和1.65 mm,且断裂后曲线稳定;单元网格尺寸为0.40 mm的模型断裂时加载位移为1.705 mm,且断裂后曲线抖动大．随着单元网格尺寸的增加,应力较大区域单元平均应力计算值偏小,使断裂时刻延后．同时,单元数目的减少会导致断裂产生和发展的突然性增加,分析时的动力效应增大．Kanvinde[7]和Liao等[10]均对断裂试件的断口进行了电镜扫描分析,得到材料特征长度为0.2～0.3 mm．因此,取单元网格尺寸为特征长度尺寸0.25 mm时,断裂预测结果具有较好的精度．

图11 不同单元网格尺寸对应的荷载-位移曲线

6 结论

1) 结合试验数据和有限元分析,校准了国产Q235B钢在单向荷载下常用延性断裂模型参数,模拟结果与试验结果吻合,且有限元分析表明,随着应力三轴度的减小,断裂等效塑性应变增大,符合钢材延性断裂理论．

2) 基于损伤因子的概念,建立了预测钢材延性断裂的VGM-DDF和JC-DDF损伤因子模型,并校准了模型参数．由损伤因子模型得到各试件断裂损伤因子值,并验证了提出的延性损伤因子模型的有效性．通过比较2种模型下各试件损伤因子的分布可知,JC-UDDF模型由于具有更多模型参数,因而展现出更小的模型离散性．

3) 试件槽口断裂模拟形态与试验形态吻合,表明损伤因子断裂模型能够准确反映钢材断裂的真实状态．不同槽口区域单元网格尺寸对断裂失效点的判别和断裂发展有影响,取单元网格尺寸为特征长度尺寸时,断裂预测结果具有较好的精度．

References)

[1] Ricles J M, Sause R, Garlock M M, et al. Posttensioned seismic-resistant connections for steel frames[J].JournalofStructuralEngineering, 2001,127(2): 113-121. DOI:10.1061/(asce)0733-9445(2001)127:2(113).

[2] Xie Q, Zhou Z, Li C, et al. Parametric analysis and direct displacement-based design method of self-centering energy-dissipative steel-braced frames[J].InternationalJournalofStructuralStabilityandDynamics, 2016: 1750087. DOI:10.1142/s0219455417500870.

[3] 王伟, 廖芳芳, 陈以一. 基于微观机制的钢结构节点延性断裂预测与裂后路径分析[J]. 工程力学, 2014, 31(3):101-108. Wang Wei, Liao Fangfang, Chen Yiyi. Ductile fracture prediction and post-fracture path tracing of steel connections based on micromechanics-based fracture criteria[J].EngineeringMechanics, 2014,31(3):101-108. (in Chinese)

[4] Argon A S, Im J. Separation of second phase particles in spheroidized 1045 steel, Cu-0.6pct Cr alloy, and maraging steel in plastic straining[J].MetallurgicalTransactionsA, 1975,6(4): 839-851. DOI:10.1007/bf02672307.

[5] Rice J R, Tracey D M. On the ductile enlargement of voids in triaxial stress fields [J].JournaloftheMechanicsandPhysicsofSolids, 1969,17(3): 201-217. DOI:10.1016/0022-5096(69)90033-7.

[6] Hancock J W, Mackenzie A C. On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states[J].JournaloftheMechanics&PhysicsofSolids, 1976,24(2/3):147-160. DOI:10.1016/0022-5096(76)90024-7.

[7] Kanvinde A M. Micromechanical simulation of earthquake-induced fracture in steel structures[D]. Palo Alto,California,USA: Department of Civil Environmental Engineering of Stanford University, 2004.

[8] Johnson G R, Cook W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J].EngineeringFractureMechanics, 1985,21(1): 31-48. DOI:10.1016/0013-7944(85)90052-9.

[9] Jia L J, Kuwamura H. Ductile fracture simulation of structural steels under monotonic tension[J].JournalofStructuralEngineering, 2013,140(5): 04013115. DOI:10.1061/(asce)st.1943-541x.0000944.

[10] Liao F, Wang W, Chen Y. Parameter calibrations and application of micromechanical fracture models of structural steels[J].StructuralEngineeringandMechanics, 2012,42(2): 153-174. DOI:10.12989/sem.2012.42.2.153.

[11] 廖芳芳, 王睿智, 李文超, 等. Q460钢基于微观机制的延性断裂判据研究[J]. 西安建筑科技大学学报(自然科学版), 2016, 48(4): 535-543,550. DOI:10.15986/j.1006-7930.2016.04.013. Liao Fangfang, Wang Ruizhi, Li Wenchao, et al. Study on micro mechanism-based ductile fracture criteria for Q460 steel[J].JournalofXi’anUniversityofArchitecture&Technology(NaturalScienceEdition), 2016,48(4): 535-543,550. DOI:10.15986/j.1006-7930.2016.04.013.(in Chinese)

[12] 周晖, 王元清, 石永久,等. 基于微观机理的梁柱节点焊接细节断裂分析[J]. 工程力学, 2015, 32(5):37-50.Zhou Hui, Wang Yuanqing, Shi Yongjiu, et al. Fracture analyses of welded details in beam-to-column connections using micromechanics-based models.[J].EngineeringMechanics, 2015,32(5):37-50. (in Chinese)

Damagefactormodelandparametercalibrationforsteelductilefractureundermonotonictension

Li Canjun1Zhou Zhen1Zhu Yazhi2Lu Lu3

(1Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education,Southeast University,Nanjing 210096,China) (2Department of Civil, Architectural and Environmental Engineering, University of Texas at Austin, Austin 78703, USA) (3State Grid Jiangsu Economic Research Institute,Nanjing 210008,China)

TU391

A

1001-0505(2017)05-0993-06

2017-02-20.

李灿军(1991—)，男，博士生；周臻(联系人)，男，博士,教授，博士生导师，seuhj@163.com.

国家自然科学基金资助项目(51208095)、江苏省“青蓝工程”资助项目、江苏省六大人才高峰资助项目(JZ-003).

李灿军,周臻,朱亚智,等.单调荷载下钢材延性断裂损伤因子模型及参数校准[J].东南大学学报(自然科学版),2017,47(5):993-998.

10.3969/j.issn.1001-0505.2017.05.024.

10.3969/j.issn.1001-0505.2017.05.024