完全图上结构异常的搜索算法——融入量子计算思维的经典算法探讨

陈汉武 李文骞 刘志昊 赵生妹

(1东南大学计算机科学与工程学院, 南京 211189)(2东南大学计算机网络和信息集成教育部重点实验室, 南京 211189)(3南京森林公安学院信息技术系, 南京 210023)(4南京邮电大学通信与信息工程学院, 南京 210003)

完全图上结构异常的搜索算法
——融入量子计算思维的经典算法探讨

陈汉武1,2李文骞1,3刘志昊1,2赵生妹4

(1东南大学计算机科学与工程学院, 南京 211189)(2东南大学计算机网络和信息集成教育部重点实验室, 南京 211189)(3南京森林公安学院信息技术系, 南京 210023)(4南京邮电大学通信与信息工程学院, 南京 210003)

散射量子行走;完全图;结构异常;不变子空间;微扰理论

Keywords: scattering quantum walk; complete graph; structural anomalies; invariant subspace; perturbation theory

搜索问题是计算机科学理论与应用技术领域的重要命题,大数据时代更是如此．AlphaGo算法很好地诠释了随机概念在大数据搜索中的重要性．根据AlphaGo搜索策略核心技术的进化历程可知,即便只从对弈的当前盘面出发去搜索博弈树的枝干,也会在有限步内很快耗尽所有计算资源．AlphaGo算法采取蒙特卡罗树搜索代替穷举搜索,即多次随机选取部分枝干进行搜索,通过计算这些搜索结果的平均值,帮助程序选出最佳走法．这种随机搜索与结果获取的思维,与量子搜索算法[1-4]的思维几乎一样,随机选取部分枝干进行搜索的思想方法在算法实践的解析中随处可见,其物理上的行为可称为随机行走．上述随机行走是经典的随机行走．基于量子力学理论的随机行走称为量子行走[5]．量子行走理论可看成是经典随机行走在量子系统中的自然推广．1993年Aharonov等[6]首次提出量子行走的概念．2003年Shenvi等[7]提出了第1个基于硬币量子行走的搜索算法(SKW算法)．2009～2010年,Childs[8]和Lovett等[9]分别证明了连续量子行走算法和离散量子行走算法可以被看作通用量子计算原型,即任意量子算法都可以被构建为基于量子行走的算法形式．

量子行走算法包括离散时间量子行走算法[10-11]和连续时间量子行走算法[12],前者又包含了硬币量子行走算法[13]和散射量子行走算法[14]．硬币量子行走算法需要一个硬币辅助空间,主要研究在图顶点上的行走;散射量子行走算法主要考察在图边上的行走,不需要辅助空间,每一步行走都在图的顶点处发生散射．硬币量子行走与散射量子行走是酉等价的[15]．2015年刘艳梅等[16]提出了一种基于星图的散射量子行走搜索算法,并证明了星图上硬币量子行走与散射量子行走的酉等价关系．

量子随机行走理论研究初期的热点主要集中在问题的数学建模、概率分布与发散速度、行走的图形拓扑结构等问题上,某些特定问题的理论研究结果指出,行走到达目标的时间较经典随机行走有着指数级加速[17-18]．随着研究的深入,研究者发现量子随机行走异于经典随机行走的一些性质,并逐步被物理实验验证[12,19-20]．随着认知的深入,2007年ACM相关会议上就已提出应将量子计算及其相关理论引入计算机软件理论的实践中．实际上量子随机行走在各种问题的解决方案都有着杰出的理论应用,例如使用量子随机行走解决元素独立性问题[21]、子集查找问题[22],甚至在密码攻击[23]上也有重要的应用．

量子随机行走搜索算法[24-26]是量子随机行走的一个重要应用,目前已有较多关于散射量子行走及其相关搜索算法的研究．文献[27-31]研究了使用散射量子行走算法搜索星图上的结构异常,并给出一般性结论．本文将散射量子行走的计算思维嵌入到完全图结构异常的经典搜索算法中,通过数学解析和Matlab程序仿真,探索经典算法融入量子计算思维的可能性．仿真结果中算法随时间延伸呈现周期性变化的特点完全符合量子计算的特征,说明主导该算法行为的内核包含了量子计算元素．最后,通过与采用邻接矩阵表示法的经典算法进行比较,说明本文算法可获得二次加速．

1 散射量子行走模型

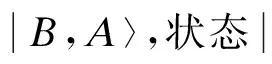
在图G(V,E)中,令V为顶点集合,E为边集合,则图G(V,E)中每个顶点j(j∈V)存在如下2个不同的子空间:

(1)

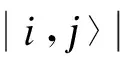
(2)

图上散射量子行走的行为可以看成是在图G中每个顶点j处执行局部酉变换Uj:Ωj→Aj．针对某一状态i,j〉,行走过程在顶点j处发生散射,即

(3)

式中,rj和tj分别表示粒子从端点i出发、在顶点j处的反射系数和透射系数．

假设完全图中包含N个顶点,分别记为1,2,…,N,每个顶点均与其他N-1个顶点相连,顶点的度d=N-1．此完全图中共有N(N-1)/2条边,对应于N(N-1)个状态,则该完全图上散射量子行走Hilbert空间H的维度为N(N-1)．

完全图中散射量子行走酉算子的作用定义为

(4)

(5)

时,此酉算子的作用等价于Grover均值反演算子:

2 悬挂点异常

定义1(悬挂点) 度为1的顶点为悬挂点．

在完全图中加入一个悬挂点(即完全图中某个异常顶点连接到一个悬挂点)时,完全图的对称性被打破,需要针对异常顶点重新定义散射量子行走酉算子．不失一般性,假设完全图中异常顶点1上连接了一个悬挂点0,N=5时完全图结构异常如图1所示．

图1 N=5时完全图的结构异常

由于异常顶点1连接了悬挂点0,顶点的度变为N,则从顶点2,3,4,5向顶点1散射,顶点1的反射系数和透射系数分别为

(6)

对于顶点0,1上发生的散射,利用Oracle查询进行一次相位翻转,以标记目标顶点．Oracle是能够在单位时间内识别特定问题满足条件的解的布尔函数,搜索算法通常以Oracle的调用次数衡量算法时间复杂度．酉算子在顶点0和1上的作用为

(7)

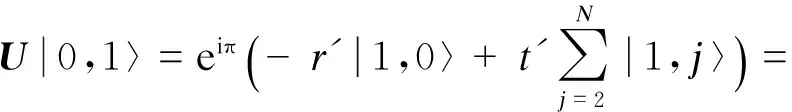
(8)

(9)

对于正常顶点2,3,…,N,顶点的度并未改变,反射系数和透射系数根据式(5)取值．使用散射量子行走搜索结构异常的算法的基本步骤如下:

① 初始化行走初态为均匀叠加态,即

(10)

② 反复执行行走酉算子U,重复n次;

③ 得到系统最终状态为

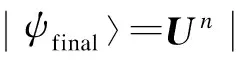
(11)

可见,算法的初始状态为完全图中所有状态的均匀叠加态,不包含关于异常顶点的任何先验知识,因此对所有顶点是等价的．迭代次数n的取值应该使得终态ψfinal〉以最大概率测得异常顶点,需要通过对酉算子U的具体分析得到．

3 算法中模型的代数推演与分析

对散射量子行走搜索算法的一般(通行)分析模式[28-29,31]为:① 找出行走空间的低维不变子空间;② 确定该子空间中酉算子U的形式;③ 通过求解U的特征值和特征向量,将行走初态用特征向量表示;④ 计算在初态上重复执行n次U算子后的终态ψfinal〉;⑤ 分析算法的时间复杂度和搜索成功的概率．

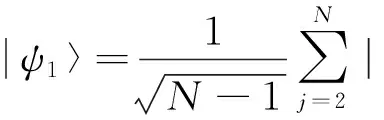
(12)

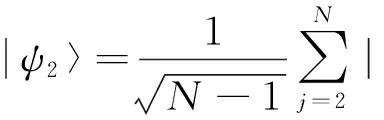
(13)

(14)

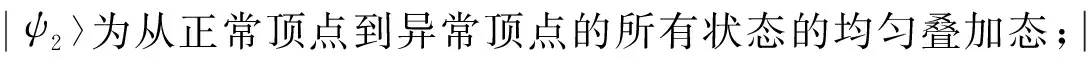
行走酉算子U对这5个状态的作用表示为

(15)

(16)

(17)

(18)

(19)

定义2(不变子空间[19]) 若T表示线性空间V的线性变换,V1表示V的子空间,且对于任意一个x∈V1,都有Tx∈V1,则称V1为T的不变子空间．

US的特征方程为

(20)

(21)

λ=-1是方程的一个根,而式(21)中的系数与N有关,无法求出确定的解．为了求解其他根,需要对其中的四阶多项式使用微扰理论．微扰理论从一个相关简单问题的精确解入手,通过加入一个微扰项到这个精确解上,寻找无法精确求解的复杂问题的近似解．

令N→∞,四阶多项式近似为

λ4-2λ3+2λ2-2λ+1=0

(22)

即

(λ-1)2(λ2+1)=0

(23)

其精确解分别为1,i,-i．取其中的二重根λ0=1进行修正,令λ=1+Δ,并代入四阶多项式中,得

(24)

(25)

(26)

行走的初态为完全图中所有状态的均匀叠加态,即

(27)

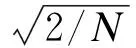
(28)

4 仿真及分析

4.1Matlab仿真

图2 N=100时搜索成功概率

图2中,N=100的完全图上行走11步后进行测量,搜索到的结果最好．在N=4,9,16,25,…,400的完全图中重复实验,找出使成功概率达到极大值所需的步数,该步数即为实验的最佳行走步数．完全图顶点个数与最佳行走步数的关系见图3．

图3 完全图顶点个数与最佳行走步数的关系

表1 行走步后测量的成功概率

4.2 经典算法分析

在经典算法中,通常采用邻接矩阵来表示图的结构．以图1中N=5的完全图为例,其邻接矩阵的表格示意图如表2所示．

表2 N=5时完全图异常的邻接矩阵表格示意图

为找出异常顶点,仅需检测任意一顶点,扫描邻接矩阵中该顶点对应的行,统计该行中出现0和1的次数．结果存在如下3种情况:① 1出现了1次,表明此顶点只与1个顶点相连,则此顶点必然是额外顶点,而与其相连的顶点必然是异常顶点．② 0出现了1次,表明此顶点与其他所有顶点都相连,则此顶点必然是异常顶点．③ 0出现了2次,表明此顶点是正常顶点．其中一次0表示该顶点与自己不通,另一次则表示该顶点与悬挂点未连接,因此可根据此次0对应的列找出悬挂点,然后扫描该悬挂点对应的行即可找出异常顶点．

根据上述分析可知,在经典算法中,扫描邻接矩阵中的任意一行,都可以在O(N)的时间复杂度内找到异常顶点．

5 结语

在计算机程序设计领域,量子随机行走的理论研究及其在搜索算法中的应用还在初期阶段．这类算法的理论设计与数学解析必须服从量子力学演算框架,需要一定的量子计算与矩阵分析的理论支持,其中酉算子(刻画量子系统演化的酉矩阵)分析是难点之一．基于量子计算刻画的任何图和结构都可以简单地写出相应的初始状态、状态空间和酉演化算子,但随着行走的进行,寻找有效的方法去分析就越发困难．因此,目前的研究对象多数只局限于特殊结构的图(包括完全图、完全二分图等高度对称的图形),以便于分析和探索融入量子计算思维的算法构造．

References)

[1] Toyama F M, van Dijk W, Nogami Y. Quantum search with certainty based on modified Grover algorithms: Optimum choice of parameters[J].QuantumInformationProcessing, 2012,12(5): 1897-1914. DOI:10.1007/s11128-012-0498-0.

[2] Liu Y, Zhang F. First experimental demonstration of an exact quantum search algorithm in nuclear magnetic resonance system[J].ScienceChinaPhysics,Mechanics&Astronomy, 2015,58(7): 1-6. DOI:10.1007/s11433-015-5661-z.

[3] Long G L. Grover algorithm with zero theoretical failure rate[J].PhysicalReviewA, 2001,64(2). DOI:10.1103/physreva.64.022307.

[4] Long G, Liu Y. Search an unsorted database with quantum mechanics[J].FrontiersofComputerScienceinChina, 2007,1(3): 247-271. DOI:10.1007/s11704-007-0026-z.

[5] Kempe J. Quantum random walks: An introductory overview[J].ContemporaryPhysics, 2009,50(1): 339-359. DOI:10.1080/00107510902734722.

[6] Aharonov Y, Davidovich L, Zagury N. Quantum random walks[J].PhysicalReviewA, 1993,48(2): 1687-1690. DOI:10.1103/physreva.48.1687.

[7] Shenvi N, Kempe J, Whaley K B. Quantum random-walk search algorithm[J].PhysicalReviewA, 2003,67(5). DOI:10.1103/physreva.67.052307.

[8] Childs A M. Universal computation by quantum walk[J].PhysRevLett, 2009,102(18): 180501. DOI:10.1103/PhysRevLett.102.180501.

[9] Lovett N B, Cooper S, Everitt M, et al. Universal quantum computation using the discrete-time quantum walk[J].PhysicalReviewA, 2010,81(4): 042330. DOI:10.1103/physreva.81.042330.

[10] Ambainis A, Bach E, Nayak A, et al. One-dimensional quantum walks [C]//ProceedingsoftheThirty-ThirdAnnualACMSymposiumonTheoryofComputing. Heraklion, Greece, 2001: 37-49. DOI:10.1145/380752.380757.

[11] Aharonov D, Ambainis A, Kempe J, et al. Quantum walks on graphs [C]//ProceedingsoftheThirty-ThirdAnnualACMSymposiumonTheoryofComputing. Heraklion, Greece, 2001: 50-59.DOI:10.1145/380752.380758.

[12] Childs A M, Farhi E, Gutmann S. An example of the difference between quantum and classical random walks [J].QuantumInformationProcessing, 2002,1(1/2): 35-43.DOI: https://doi.org/10.1023/A:1019609420309.

[13] Ambainis A, Kempe J, Rivosh A. Coins make quantum walks faster [C]//ProceedingsofthesixteenthannualACM-SIAMsymposiumondiscretealgorithms. Philadelphia, USA, 2005: 1099-1108.

[14] Hillery M, Bergou J, Feldman E. Quantum walks based on an interferometric analogy [J].PhysicalReviewA, 2003,68(3):032314. DOI:10.1103/physreva.68.032314.

[15] Andrade F M,da Luz M G E. Equivalence between discrete quantum walk models in arbitrary topologies [J].PhysicalReviewA, 2009,80(5): 052301. DOI:10.1103/physreva.80.052301.

[16] 刘艳梅, 陈汉武, 刘志昊, 等. 星图上的散射量子行走搜索算法[J]. 物理学报, 2015, 64(1): 010301. DOI:10.7498/aps.64.010301. Liu Yanmei, Chen Hanwu, Liu Zhihao, et al. Scattering quantum walk search algorithm on star graph[J].ActaPhysicaSinica, 2015,64(1): 010301. DOI:10.7498/aps.64.010301.(in Chinese)

[17] Childs A M. On the relationship between continuous-and discrete-time quantum walk [J].CommunicationsinMathematicalPhysics, 2010,294(2): 581-603. DOI:10.1007/s00220-009-0930-1.

[18] Kempe J. Discrete quantum walks hit exponentially faster[J].ProbabilityTheoryandRelatedFields, 2005,133(2): 215-235. DOI:10.1007/s00440-004-0423-2.

[19] Travaglione B C, Milburn G J. Implementing the quantum random walk[J].PhysicalReviewA, 2002,65(3). DOI:10.1103/physreva.65.032310.

[20] Wang C, Li Y, Hao L. Optical implementation of quantum random walks using weak cross-Kerr media[J].ChineseScienceBulletin, 2011,56(20): 2088-2091. DOI:10.1007/s11434-011-4545-5.

[21] Xue P, Zhang R, Qin H, et al. Experimental quantum-walk revival with a time-dependent coin [J].PhysicalReviewLetters, 2015,114(14): 140502. DOI:10.1103/PhysRevLett.114.140502.

[22] Ambainis A. Quantum walk algorithm for element distinctness [J].SIAMJournalonComputing, 2007,37(1): 210-239. DOI:10.1137/s0097539705447311.

[23] Childs A M, Eisenberg J M. Quantum algorithms for subset finding [J].QuantumInformation&Computation, 2003,5(7):593-604.

[24] Wang H, Ma Z, Ma C. An efficient quantum meet-in-the-middle attack against NTRU-2005[J].ChineseScienceBulletin, 2013,58(28): 3514-3518. DOI:10.1007/s11434-013-6020-y.

[25] Lee J, Lee H W, Hillery M. Searches on star graphs and equivalent oracle problems [J].PhysicalReviewA, 2011,83(2): 022318. DOI:https://doi.org/10.1103/PhysRevA.83.022318.

[27] Reitzner D, Hillery M, Feldman E, et al. Quantum searches on highly symmetric graphs [J].PhysicalReviewA, 2009,79(1): 012323. DOI:10.1103/physreva.79.012323.

[28] Feldman E, Hillery M, Lee H W, et al. Finding structural anomalies in graphs by means of quantum walks [J].PhysicalReviewA, 2010,82(4): 83-79. DOI:https://doi.org/10.1103/PhysRevA.82.040301.

[29] Hillery M, Zheng H, Feldman E, et al. Quantum walks as a probe of structural anomalies in graphs [J].PhysicalReviewA, 2012,85(6): 062325. DOI:10.1103/physreva.85.062325.

[30] Cottrell S, Hillery M. Finding structural anomalies in star graphs using quantum walks[J].PhysRevLett, 2014,112(3): 030501. DOI:10.1103/PhysRevLett.112.030501.

[31] 薛希玲, 李文骞, 陈汉武, 等. 基于 Grover 硬币算子的量子行走在商图上的演化算子[J]. 电子学报, 2016, 44(3): 555-559. DOI:10.3969/j.issn.0372-2112.2016.03.009. Xue Xiling, Li Wenqian, Chen Hanwu, et al. The evolutionary operator of quantum walks with Grover coin on quotient graph[J]. 2016, 44(3): 555-559. DOI:10.3969/j.issn.0372-2112.2016.03.009.(in Chinese)

Searchalgorithmofabnormalstructureoncompletegraph:Discussionofclassicalalgorithmmergedintothequantumcomputingthinking

Chen Hanwu1,2Li Wenqian1,3Liu Zhihao1,2Zhao Shengmei4

(1School of Computer Science and Engineering, Southeast University, Nanjing 211189, China) (2Key Laboratory of Computer Network and Information Integration of Ministry of Education, Southeast University, Nanjing 211189,China) (3Department of Information Technology, Nanjing Forest Police College, Nanjing 210023,China) (4College of Telecommunications and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210003,China)

TP387

A

1001-0505(2017)05-0866-07

2017-02-20.

陈汉武(1955—)，男，博士，教授，博士生导师，hw_chen@seu.edu.cn.

陈汉武,李文骞,刘志昊,等.完全图上结构异常的搜索算法:融入量子计算思维的经典算法探讨[J].东南大学学报(自然科学版),2017,47(5):866-872.

10.3969/j.issn.1001-0505.2017.05.005.

10.3969/j.issn.1001-0505.2017.05.005