改进蚁群算法在盘磨进退刀控制中的应用

李 茜 佘 都 汤 伟

(陕西科技大学电气与信息工程学院，陕西西安，710021)

·盘磨进退刀控制·

改进蚁群算法在盘磨进退刀控制中的应用

李 茜 佘 都*汤 伟

(陕西科技大学电气与信息工程学院，陕西西安，710021)

在制浆过程中，盘磨进退刀控制直接影响着纸浆的质量。PID控制算法因其结构简单、易实现等优点而被广泛应用于造纸工业中。然而，PID参数不易整定且易产生超调和震荡，这会导致在盘磨进退刀控制中出现碰刀问题，使盘磨磨片遭到磨损，进而影响纸浆正常生产。本课题在基本蚁群算法基础上提出了一种改进蚁群算法并将其用于PID参数整定。MATLAB仿真结果表明，该方法可以快速、准确地找到最佳的PID固定参数，解决了传统PID整定方法过分依赖人工经验、耗时长等问题。

盘磨进退刀控制；PID控制；改进蚁群算法；MATLAB仿真

打浆过程是制浆造纸过程中极为重要的一步，素有“三分造纸，七分打浆”之说。打浆是指通过盘磨对浆料中的纤维进行处理，使其发生物理化学变化从而获得某些方面的特性，以满足纸或纸板生产的工艺指标要求。在自动控制过程中，盘磨控制采用间隙控制方式，通过控制主电机功率、进浆浓度和流量，从而改变盘磨间隙来控制打浆度[1]。在控制中如果整定超调过大，盘磨的进刀过多，容易造成严重的生产事故——碰刀[2]，相反，如果盘磨退刀过多，磨盘间隙变大，间隙中浆料含量过多且盘磨内水流量大，导致一部分浆料不能被剪切，温度升不到位。这种情况下虽然盘磨机功耗降低了，但是纤维的状态不稳，纤维抗拉强度低，外观比较粗糙，会降低纸张质量和使用寿命[3- 4]。盘磨是主要的打浆设备，对其进行准确地自动控制会影响整个生产进程[5]。因此，盘磨间隙的控制算法必须安全可靠。

PID算法具有结构简单、易于实现、适应性强等优点，在我国造纸行业中被广泛采用。传统的PID算法参数主要是通过人工经验调整，不仅参数不易整定，还费时、耗力。常用来整定PID算法参数的方法有临界比例度法、Z-N法、衰减曲线法等。近年来，随着人工智能的发展，这些传统的整定方法逐渐被代替。20世纪90年代初提出的蚁群算法(ant colony algorithm，简称ACO)是基于种群模式的启发式算法，采用分布式正反馈并行机制，具有较强的鲁棒性，编程简单易实现，已成为解决优化问题的一种有效手段。本课题将对基本蚁群算法进行改进，并将其用于优化盘磨进退刀功率控制器的参数中。

1 盘磨进退刀控制原理

打浆过程控制的发展大致可以分为三个阶段：比能量控制、游离度控制和比能量——比边缘负荷控制。典型的比能量控制系统主要有以下三种：恒功率控制、温差控制、单位时间内绝干浆料能耗控制(Hqb/t)[7]。实践证明最理想的控制方式是通过控制盘磨进刀量来直接控制打浆度。然而，这种方法在实践上有一定的技术难度。目前，恒功率控制方式在我国的纸浆生产线上应用仍最为广泛，其控制系统框图如图1所示。

图1 恒功率控制系统流程图

图1中Pset为恒功率控制人为给定的功率设定值，通过安装在主电机柜中的功率变送器反馈功率当前值P，从而计算出功率偏差，输入至功率控制变频器输出进退刀脉冲，从而调节功率，进而间接达到调节盘磨间隙的目的。本课题主要是基于这种控制方式加以改进，从而优化PID算法参数。打浆过程的传递函数可近似看成式(1)[8]。

(1)

PID控制是用于过程控制最有效的方式之一，其控制器具有结构简单，适应性强等优点，PID控制器结构框图如图2所示。

图2 PID控制器原理图

图2中r为设定值，y为系统的输出值，控制量u与偏差e=r-y满足数学表达式(2)。

(2)

式中，Kp为比例因子；Ti为积分时间常数；Td为微分时间常数；Ki=Kp/Ti为积分系数；Kd=Kp*Td为微分系数。

2 基本蚁群算法

蚁群算法由意大利学者M.Dorigo于1991年在他的博士论文中首次提出，并用其成功解决了旅行商问题(TSP)。下面就以TSP说明蚁群系统(AS)[9]。

TSP可以用一个带权完全图G=(N，A)来描述，其中N是城市的节点集合，N={1，2，...n}。A={i，j}，(i，j)表示城市i和j组成的边，d表示城市i和j之间的距离。TSP的目标是寻找一条具有最小成本值的汉密尔顿回路，这里的汉密尔顿回路指的是一条访问G中的每一个节点有且仅有一次的闭合路径。这样，TSP的一个最优解就对应于节点标号为N={1，2，...，n}的一个排列π，并且使得f(π)最小，f(π)定义为式(3)。

(3)

在AS中，m只人工蚂蚁并行地构建TSP路径，在路径构建的每一步中，蚂蚁k按照一个称之为随机比例规则的概率行为选择规则，来决定下一步将移向哪一个城市。当位于城市i的蚂蚁k选择j作为下一个访问城市的概率，具体计算如式(4)所示。

(4)

当所有蚂蚁构建完路径后，各边上的信息素将会被更新。首先，所有边上的信息素都会减少一个常量因子的大小，信息素的蒸发如公式(5)所示。

τij←(1-ρ)τij，∀(i，j)∈A

(5)

式中，ρ为信息素蒸发率，0≤ρ≤1。参数ρ的作用是避免信息素的无限积累，而且还可除去算法之前选用较差的路径。然后，所有蚂蚁根据各自构建的路径长度，在它们经过的边上释放的信息素如式(6)所示。

(6)

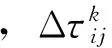
(7)

式中，Ck为第k蚂蚁建立的路径的长度，即所有边的长度之和。

3 改进优化蚁群算法的PID参数整定

3.1传统蚁群算法的改进

基本蚁群算法搜索到一定程度后，所有蚂蚁都会选择同一条路径，这样不利于算法对解空间的进一步搜索，算法会过早地收敛并陷入局部最优的困境[10]。过早出现这种现象的原因是按照固定不变的模式去更新信息量和确定每次路径的选择概率。为此，本课题在基本蚁群算法的基础上对信息素的更新策略进行了改进，改进后的信息素释放规则如式(8)所示。

(8)

式中，Δτbest=Q/Cmin，pk=Ck/Cmax；Cmin为本次优化中最优路径对应的最短路径距离；Cmax为本次寻优中最差路径对应的最长路径距离；Ck为本次寻优中蚂蚁k经过的路径对应的路径距离。

用如式(9)所示的坐标点表示待优化路径上的城市坐标位置，本课题蚁群算法蚂蚁的数目100，算法的最大迭代次数为60，信息素蒸发率ρ=0.3。

(9)

图3 最短路径优化结果

改进前后的蚁群算法优化的结果如图3所示。图3表明，ACO在第8次迭代时已找到最短路径；而改进ACO在迭代次数达到30时，才找到最短路径，且最短路径比ACO优化的最短路径更短，因此，改进ACO在一定程度上解决了算法过早收敛而陷入局部最优的问题。

基于改进蚁群算法的PID控制就是在PID控制的基础上引入改进蚁群算法，通过改进蚁群算法动态调节PID控制参数kp、ki及kd，最终得到良好的控制效果。其控制流程如图4所示。

图4 基于改进蚁群算法的PID控制系统

大量研究表明，通过蚁群算法可将问题以图表形式表示出来，再根据参数kp、ki、kd的取值范围，用5位有效数字表示每一个参数，小数点前一位，小数点后四位，结果如图5所示[11]。

图5 蚂蚁爬行路径图

其中虚线上及虚线内的节点表示蚂蚁可以爬行的节点，其中x和y的交点[x，yx]表示蚂蚁可以到达的节点，其中x为整数，取值范围为[0～15]；y为整数，取值范围为[0～9]，其中每一个整数代表每个有效位的取值。

为了获得合适的过渡过程的动态性能，本课题采用式(10)作为选择参数的最小目标函数。为了防止控制量过大，在目标函数中加入控制器输出的平方项。

(10)

式中，e(t)为系统误差；u(t)为控制器输出；w1、w2和w3为权值。

为避免超调对盘磨造成的碰刀问题，本课题采用惩罚功能，即一旦产生超调，将超调量做为最优指标的一项，此时最优指标的计算按照式(11)。

(11)

式中，w4>>w1；ey(t)=y(t)-y(t-1)。

3.2改进ACO优化PID参数步骤

3.2.1初始条件设定及参数初始化

(1)设蚁群中蚂蚁的数目为m=100，算法最大

迭代次数为NCmax=60，信息素蒸发率ρ=0.3。

(2)设蚂蚁的初始路径(当前最优路径)为：

(0，0)→(1，0)→(2，9)→(3，6)→(4，8)→(5，1)→(6，0)→(7，1)→(8，2)→(9，9)→(10，4)→(11，1)→(12，6)→(13，4)→(14，5)→(15，8)。

(3)设各节点初始信息素浓度τ0(x，yx)为常数。

3.2.2PID参数优化过程

(1)将蚂蚁全部放置起点(0，0)，蚂蚁开始爬行，第k只蚂蚁爬行至下一节点的路径选择概率按公式(4)计算，启发式因子定义为式(12)。

(12)

图6 系统仿真模型

蚂蚁按照上述过程完成一次爬行过程，并将蚂蚁经过的每个有效位上的数值放入数组y中，按式(13)计算PID控制器的3个参数。

kp=y(1)*100+y(2)*10-1+y(3)*10-2+y(4)*10-3+y(5)*10-4

ki=y(6)*100+y(7)*10-1+y(8)*10-2+y(9)*10-3+y(10)*10-4

kd=y(11)*100+y(12)*10-1+y(13)*10-2+y(14)*10-3+y(15)*10-4

(13)

(2)计算每只蚂蚁爬行结果的目标函数值fk。

(3)按照式(8)进行节点信息素更新。

(4)进行第2次循环，如果本次循环有找到更优的kp、ki、kd，就替换原来的参数……，直到全部循环结束。

(5)输出最优结果。

4 仿真结果

在MATLAB中，分别采用工程整定法(Z-N)、ACO和改进ACO整定PID控制器参数，并在simulink中搭建仿真模型，见图6。基于三种方法整定的控制系统阶跃响应及在100 s时加入10%的输入干扰响应的结果如图7所示。

图7 控制系统阶跃响应曲线

三种方法的阶跃响应动态指标如表1所示。从图7和表1中可以看出，相比于ACO和Z-H来说，改进ACO的PID控制系统响应速度快，无超调量，具有优异的动态性能。干扰作用下控制系统动态性能指标如表2所示。

从图7和表2可以看出，三种方法都可以再次达到稳态，但是Z-N曲线和ACO曲线再次返回到稳态的时间长并且出现了较大的超调量。而改进ACO曲线在干扰过程中趋于稳定状态的时间短，且过渡平缓。因此，基于改进ACO的PID参数寻优控制具有较好的抗干扰性能和自适应性能。

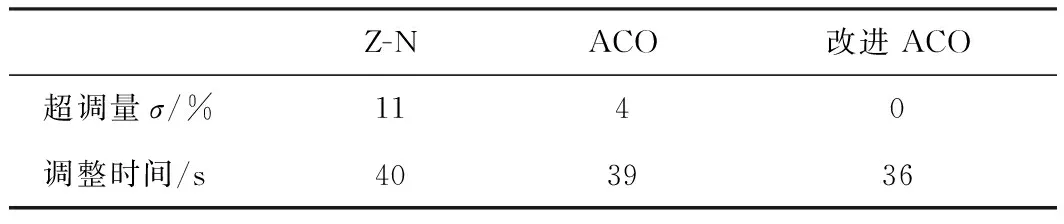
表1 系统阶跃响应动态性能指标

表2 干扰信号下系统动态性能指标

为了进一步研究改进ACO的鲁棒性，针对参数摄动这类情况，改变被控对象参数，比较三种整定方法的鲁棒性。

当被控对象参数K和T同时增加10%，其余参数不变时的控制系统阶跃响应曲线如图8所示。三种方法的动态性能指标如表3所示。

图8 K、T同时增加10%时控制系统阶跃响应曲线

Z-NACO改进ACO超调量σ/%1680调整时间/s403720

图9 K、T和τ同时增加10%时系统响应曲线

当被控对象参数K、T和τ同时增加10%，其余参数不变时的控制系统阶跃响应曲线，如图9所示。三种方法的动态性能指标如表4所示。

表4 K、T和τ增加10%时系统动态性能指标

当被控对象参数K、T和τ同时增加20%，其余参数不变时控制系统阶跃响应曲线，如图10所示。动态性能指标如表5所示。

图10 K、T和τ同时增加20%时系统响应曲线

Z-NACO改进ACO超调量σ/%36215调整时间/s544034

当被控对象参数摄动时，从图8和图9及表2和表4可以看出，改进ACO曲线产生的超调量最小，且到达稳态的调整时间最短，保持了良好的动态性能；而在图10和表5中，Z-N曲线和ACO曲线产生了明显的振荡波动，改进ACO曲线只产生了小幅度的超调量。

通过以上仿真结果的比较，结果表明,基于改进ACO优化的PID参数比其他两种方法具有更快的响应速度、更优的抗干扰性能和鲁棒性能。因此，对于盘磨机进退刀控制的大时滞、大惯性等特点，改进ACO更适用于盘磨进退刀控制的PID参数整定。

5 结 论

通过以上研究表明，基于改进ACO的盘磨机进退刀控制具有响应速度快、较好的抗干扰性能和鲁棒性能，能够很好地确保盘磨进退刀控制的精度，同时也可解决盘磨机碰刀的问题。另外，在一定程度上也可提高打浆效果和产品的生产质量。

[1] WANG Jia-hui, WANG Ping. Research Status and Development Trend of DiscRefiner[J]. China Pulp & Paper, 2014, 33(9)： 51． 王佳辉, 王 平. 盘磨机的研究现状与发展趋势[J]. 中国造纸, 2014, 33(9)： 51．

[2] WANG Ping, LIN Jian-tao, WANG Gao-feng, et al. Plate Collision of Disc Refiner and Its Prevention[J]. China Pulp & Paper, 2014, 33(11): 37． 王 平, 林建涛, 王高峰, 等. 盘磨机的碰盘及其预防措施[J]. 中国造纸, 2014, 33(11): 37．

[3] TANG Wei, QIU Jin-qiang, LIU Qing-li, et al. Application and Implement of Refiner Control System Based on S7- 400 Programmable Logic Controller[J]. China Pulp & Paper, 2016, 35(5): 51． 汤 伟, 邱锦强, 刘庆立, 等. 基于S7- 400PLC的三盘磨浆机控制系统的应用与实现[J]. 中国造纸, 2016, 35(5): 51．

[4] WANG Zhong-feng, TANG Wei, LIU Qing-li, et al. Design and Application of Human-simulated Intelligent PID in APMP Refiner Control[J]. Control and Instruments in Chemical Industry, 2010, 37(12)：11． 王忠峰, 汤 伟, 刘庆立, 等. 仿人智能PID在APMP盘磨控制中的设计与应用[J]. 化工自动化及仪表, 2010, 37(12)：11．

[5] WANG Meng-xiao, MIU Hai-feng, JIANG Li-bo. Improvement of Refiner Control and Application of Expert System[J]. China Pulp & Paper, 2007, 26(1): 37． 王孟效, 缪海峰, 姜丽波. 盘磨控制的改进及专家系统在其中的应用[J]. 中国造纸, 2007, 26(1): 37．

[6] CHEN Shuai-shuai, ZHAO Qian-mei, XIONG Zhi-xin, et al. Application of the PID Parameters Self-tuning Based on IPSO in Headbox Total Pressure Control[J].China Pulp & Paper, 2015, 34(11): 37． 陈帅帅, 赵倩梅, 熊智新, 等. 基于IPSO的PID参数自整定在流浆箱总压控制中的应用[J]. 中国造纸, 2015, 34(11): 37．

[7] QIU Jin-qiang. Research and Implementation of Pulp Refining Control System for Medium and High Speed Tissue Paper Machine[D]. Xi’an: Shaanxi University of Science and Technology, 2016. 邱锦强. 中高速卫生纸机打浆控制系统的研究与实现[D]. 西安： 陕西科技大学, 2016．

[8] Li Ru-lin, ZHANG Gen-bao, Li Qin-yong. Design of Plate Mill Controller Based on Predictive Fuzzy/PID[J]. Control and Instruments in Chemical Industry, 2010, 37(5)： 26． 李如林, 张根宝, 李勤勇.基于预测模糊/PID控制的盘磨控制器设计[J]. 化工自动化仪表, 2010, 37(5)： 26．

[9] M Dorigo, TStützle. Ant Colony Optimization[M]. Cambridge, MA: MIT Press/Bradford Books, 2004.

[10] DUAN Hai-bin. Ant Colony Algorithm and Its Application[M]. Beijing: Science Press, 2005． 段海滨. 蚁群算法原理及其应用[M]. 北京： 科学出版社, 2005．

(责任编辑：吴博士)

ApplicationofImprovedAntColonyAlgorithmintheCutterControlofDiscRefiner

LI Qian SHE Du*TANG wei

(CollegeofElectricalandInformationEngineering,ShaanxiUniversityofScienceandTechnology,Xi’an,ShaanxiProvince, 710021)

In the process of pulping, the cutter control of disc refiner affects the quality of the pulp directly.PID control algorithm is widely used in paper industry because of its characteristics of simple structure and easy to implement. But PID parameter is difficult to set and easy to produce super harmonic and oscillation, which could often cause knife collision problem in disc cutter control, making the disc plate to wear, then influence the normal production of pulp. Based on the basic ant colony algorithm, this paper presented an improved ant colony algorithm and used it to set the PID parameters, this method overcomed the problem of over reliance on artificial experience and time consuming.MATLAB simulation results showed that the method could find the optimal control parameters quickly and accurately．

the cutter control of refiner;PID control; improved ant colony algorithm; MATLAB simulation

李 茜女士，硕士，教授；研究方向：工业自动化与智能控制。

TP273

A

10.11980/j.issn.0254- 508X.2017.09.010

2017- 02- 27(修改稿)

陕西省工业攻关项目(2012K09-10)。

*通信作者：佘 都，在读硕士研究生；主要研究方向：工业自动化与智能控制。

(*E-mail: 1479029841@qq.com)