基于遗传算法优化BP神经网络预测CO2/H2S环境中套管钢的腐蚀速率
万里平,徐友红,冯兆阳,孔 斌,杨 兵
基于遗传算法优化BP神经网络预测CO2/H2S环境中套管钢的腐蚀速率
万里平1,徐友红1,冯兆阳1,孔 斌1,杨 兵2
(1.西南石油大学油气藏地质及开发工程国家重点实验室,成都610500;2.大庆石油管理局松原机械总厂,松原138000)
基于CO2/H2S共存腐蚀环境的复杂性、危险性,以及两者协同与竞争效应的不确定等原因,套管钢在CO2/H2S共存腐蚀环境中腐蚀速率测试存在试验时间长、误差较大且存在不安全隐患等缺陷,现有的单一腐蚀速率预测模型不能满足这方面的研究。利用建立的遗传算法优化BP神经网络模型分别对不同温度、不同CO2分压和不同H2S分压条件下套管钢的腐蚀速率进行预测。与单纯的BP神经网络模型预测相比,遗传算法优化BP神经网络训练收敛速率有所增加,预测效果得到改善;遗传算法优化BP神经网络预测值与实测值吻合较好,此预测模型可靠性很强;该方法为我国高酸性气田开发中快速获取腐蚀速率数值提供了一条新的思路。
遗传算法;酸性气田;腐蚀速率;BP神经网络;H2S腐蚀
Abstract:Due to the complexness,riskiness and uncertainty of coordination and synergic effect of corrosion in CO2/H2Senvironment,the corrosion rate testing of casing steel needs a long time test and shows relatively large error and existence of hidden dangers in CO2/H2Senvironment,and the existing single corrosion rate prediction model cannot meet the demands in the research.The established model of BP artificial neural network optimized by genetic algorithm was used to test the corrosion rates at different temperature,CO2pressure and H2S pressure.Compared to the BP neural network,the BPartificial neural network optimized by genetic algorithm increased the convergence rate of train and improved the effect of forecast,and the values from both prediction and actual measurement of BP artificial neural network optimized by genetic algorithm were in good agreement.This model also had a strong reliability.This method provides us a new way to acquire the figure of the corrosion rates fast in high acidy oil-gas field.
Key words:genetic algorithm;sour gas field;corrosion rate;BP neural network;H2S corrosion
CO2/H2S腐蚀是石油天然气工业中常见的腐蚀类型,也是目前腐蚀与防护领域中重要的研究课题。影响CO2/H2S腐蚀速率的因素很多,如CO2/H2S分压、温度、p H、压力、矿化度、时间以及材质等[1-3]。目前,已有的模型多聚焦于H2S致开裂,而H2S单独作用对腐蚀速率影响的模型较少[4]。此外,有关CO2单独作用对腐蚀速率影响的模型较多。Shell公司的De Waard 95模型[5]将腐蚀环境温度、介质流速、p H等影响因素融入模型,但在高温和高p H条件下预测的腐蚀速率比实测值稍大;Norsok M506预测模型[6]与De Waard 95预测模型的结果相反,此模型在高温和高p H条件下预测结果比实测值稍小。有关CO2和H2S共同作用对腐蚀速率预测的模型也不多,商杰等[7]建立了基于遗传算法的BP(Back Propagation)网络模型,并在预测油管钢腐蚀速率中进行了应用。李强等[8]运用MATLAB编程建立了预测油气管线腐蚀速率的网络模型。本工作在前人研究的基础上利用BP神经网络和遗传算法优化BP神经网络两种模型对CO2/H2S环境中套管钢腐蚀速率进行预测并检验其可靠性。
1 基于BP神经网络预测
1.1 BP神经网络结构
按神经网络的互联结构,误差反向传播神经网络(BPNN)属于前馈型神经网络。1986年RUMELHART,HINTON和WILLIAMS完整而简明地提出这种算法,系统地解决了多层神经网络中隐单元层连接权的学习问题,并在数学上给出了完整的推导。BP神经网络模型是目前人工神经网络中应用最为广泛的模型,一般为三层网络,即输入层、隐含层和输出层,如图1所示。
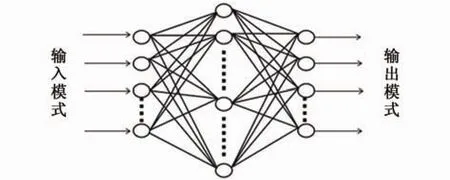
图1 BP神经网络结构Fig.1 The structure of BP neural network
1.2 样本数据
综合考虑各因素对套管钢腐蚀速率的影响程度及实测数据的可获得性,以CO2分压,H2S分压和温度作为输入量,以腐蚀速率实测值作为输出量,基于BP神经网络建立套管钢腐蚀速率预测模型。结合利用中石油管材研究院和河南科技大学共同研究的关于N80套管钢在CO2/H2S环境中腐蚀试验数据[9],一共选取了26组试验数据进行BP神经网络模型的训练和验证,其中有22组数据作为训练样本(见表1),4组数据作为检测样本(见表2)。
1.3 网络结构及参数
采用三层BP神经网络模型,其结构为3-L-1形式,即输入层有3个节点,隐含层有L个节点,输出层有1个节点,已有研究证明隐含层节点数的选择直接影响到BP神经网络的性能,其经验公式如式(1)所示。


表1 训练样本数据Tab.1 Training sample data

表2 测试样本数据Tab.2 Test sample data
式中:L为隐含层节点数;n为输入层节点数;m为输出层节点数;a为1~10之间的调节常数。
关于隐含层节点数的选择迄今没有科学的定论,主要是借助于经验公式和实际经验,可以参照式(1)进行设计。
经过多次不断尝试变化隐含层节点数,当隐层节点为6、7或者8时,与其他不同隐含层节点数值时的网络训练均方误差较小,因此在本次操作中取隐含层节点数为8,此BP神经网络结构简图见图2。
进行网络训练前将各输入参数进行归一化处理,即将数据处理为区间[0,1]之间的数据,本工作中采用Matlab软件工具箱中的mapminmax函数将所有样本数据归一到[0,1]之间。

图2 BP神经网络结构图Fig.2 Structure diagram of BP neural network
网络中输入层到隐含层的传递函数采用S型的logsig函数,隐含层到输出层的传递函数采用purelin函数,网络训练采用trainlm函数。同时,学习速率的选取很重要,在实际操作过程中为了保证系统的稳定性,一般倾向于选取较小的学习速率,通过观察误差下降曲线来判断,最终确定学习速率为0.05。为了要求训练结果达到一定精度又防止网络出现过拟合现象,最终确定目标误差为0.005。为了在网络训练过程中有效减小震荡趋势、改善其收敛性和抑制陷入局部极小值等现象,最终确定动量系数为0.9。最大训练次数为500次。编写程序后,在Matlab中进行仿真。
1.4 仿真结果
1.4.1 BP神经网络的训练误差曲线
通过BP神经网络不断反复学习训练,其训练误差不断降低,当达到预定的误差值时,网络训练便会自动停止。由图3可见:经过228次训练后达到要求的目标误差0.005。

图3 BP神经网络训练收敛过程图Fig.3 The process diagram of convergence training by BP neural network
1.4.2 BP神经网络预测值与实测值对比分析
对之前进行过归一化的测试样本数据进行仿真预测后,需对预测结果进行反归一化处理,然后再与实测值进行比较,其结果如表3所示。
由表3可见:预测值与实测值之间存在误差,但其相对误差小于20%,产生误差是因为训练样本数据量有限,影响了该模型的训练能力和网络的泛化能力。

表3 BP人工神经网络预测值与实测值比较Tab.3 Comparison between prediction and actual measurement of artificial neural network
2 基于遗传算法优化BP神经网络预测
2.1 建立模型
遗传算法优化BP神经网络算法的基本原理是首先利用遗传算法来优选BP神经网络的初始化权值和阀值,并构建初始的网络结构,再把优化后的权值和阈值重新赋给BP神经网络进行学习训练,重复循环,以达到避免网络训练陷入局部极小值的目的。充分发挥遗传算法和BP神经网络的各自优势,将两者结合应用已经逐渐成为一个十分有前景的研究热点[9]。
采用三层网络结构,输入层神经元数为3个,即分别代表H2S分压,CO2分压和温度;隐含层的神经元数为8个;输出层的神经元数为1个,即腐蚀速率,网络的权值和阀值是通过随机函数来初始化的。采用遗传算法优化BP神经网络的初始权值和阈值,其种群规模为10,最大进化代数为15,交叉概率为0.6,变异概率为0.05。和前面单纯的BP神经网络模型一样,网络中输入层到隐含层的传递函数采用S型的logsig函数,隐含层到输出层的传递函数采用purelin函数,网络学习训练采用trainlm函数,确定网络学习速率为0.05,目标误差为0.005,动量系数取值为0.9,最大训练次数为500次。
2.2 预测结果分析
2.2.1遗传算法的训练误差曲线
遗传算法中个体的适应度大小直接影响到遗传算法的收敛速率和能否找到全局最优解,同时还可以评价个体对环境的适应程度,适应度越大说明个体适应性好,反之则表示个体适应性差。由图4可见,经过67次训练后达到要求的目标误差0.005。
2.2.2遗传算法预测值与实测值对比分析
网络训练好后,对测试样本数据进行仿真预测,然后再对仿真预测的结果进行反归一化处理后与实测值进行比较以判断其可靠性,其结果如表4所示。

图4 网络训练收敛过程图Fig.4 The process diagram of convergence training by network
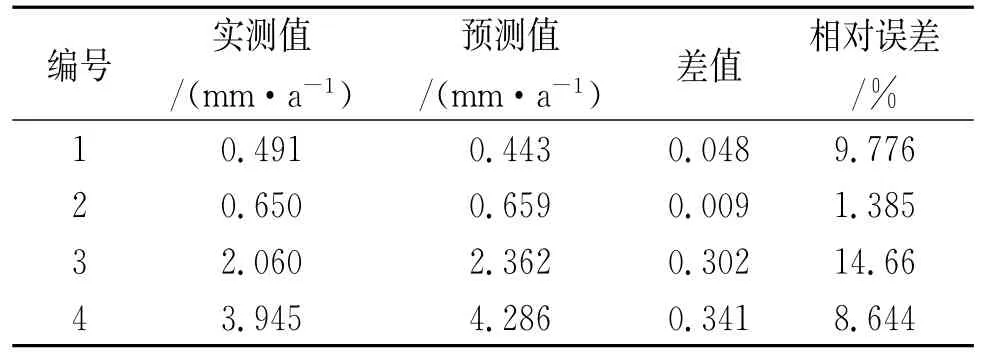
表4 遗传算法优化BP人工神经网络预测值与实测值比较Tab.4 Comparison between prediction and actual measurement of BP artificial neural network optimized by genetic algorithm
2.2.3遗传算法优化结果
经过遗传算法优化BP神经网络的权值和阀值,再通过训练后达到预定的误差要求后,得到最终的权值矩阵和阀值矩阵如下:
(1)输入层到隐含层的权值矩阵:

(2)隐含层的阀值矩阵:

(3)隐含层到输出层的权值矩阵:

(4)输出层的阀值矩阵:
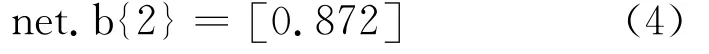
2.2.4温度对套管钢腐蚀速率的影响
设定 CO2分压为1.5 MPa,H2S分压为0.6 MPa,确定旋转装置转速为256 r/min(即高温高压釜内动态流速为1 m/s),考察不同温度条件下(从40℃逐级增加到140℃,每级增加5℃)N80套管钢的液相腐蚀速率变化规律,试验所得值为实测值;利用建立的遗传算法优化BP神经网络模型预测不同温度条件下的腐蚀速率变化,所得值为预测值;将预测值与实测值进行对比,如图5所示。

图5 不同温度条件下的腐蚀速率预测值与实测值对比Fig.5 Comparison between prediction and actual measurement of corrosion rates at different temperatures
由图5可见:实测值与预测值吻合较好,具有较高的相关性。这主要是因为在该网络中参与学习训练的过程中温度变化幅度并没有呈现有突变的趋势,变化曲线相对比较柔和,网络学习训练相对较简单;另一方面,参与网络学习训练的数据相对较多,所以该模型的预测值能够比较精确地展现出温度对腐蚀速率的影响。
2.2.5 CO2分压对套管钢腐蚀速率的影响
设定温度为100℃,确定腐蚀介质流速为1 m/s,H2S分压为0.6 MPa和0.015 MPa时,考察不同CO2分压条件下N80套管钢的腐蚀速率变化规律,试验所得值为实测值;利用建立的遗传算法优化BP神经网络模型预测不同CO2分压条件的腐蚀速率变化规律,所得值为预测值;将预测值与实测值进行对比,如图6所示。
由图6可见:实测值与预测值吻合的比较好,这是因为在该网络中参与学习训练的过程中CO2分压变化曲线并没有呈现有突变的趋势,其变化曲线相对比较柔和,网络能够容易地判断其变化规律,从而预测精度就比较高;且实测值曲线和预测值曲线均呈现出随CO2分压升高而增大,误差也较小。
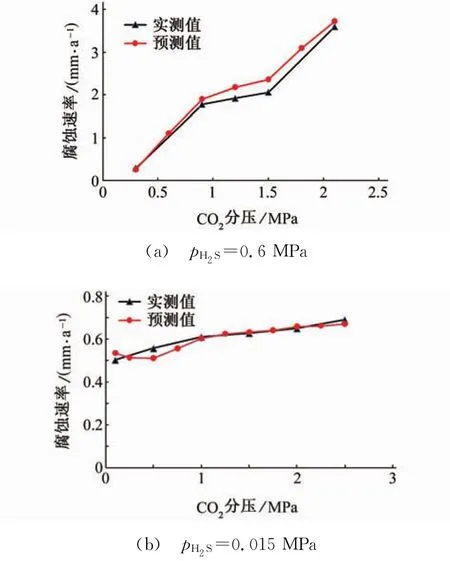
图6 不同CO2分压条件下腐蚀速率预测值与实测值对比Fig.6 Comparison between prediction and actual measurement of corrosion rate under different CO2pressure
2.2.6 H2S分压对套管钢腐蚀速率的影响
设定温度为100℃,确定腐蚀介质流速为1 m/s,CO2分压为1.5 MPa和1.2 MPa时,考察不同H2S分压条件下N80套管钢的腐蚀速率变化规律,试验所得值为实测值;利用建立的遗传算法优化BP神经网络模型预测不同H2S条件下的腐蚀速率变化,所得值为预测值;将预测值与实测值进行对比,如图7所示。
由图7可见:CO2分压为1.5 MPa时,预测值与实测值吻合的较好,即使在变化曲线中出现了腐蚀速率突变,但是网络通过学习训练后仍然能够辨别出其变化规律;CO2分压为1.2 MPa时,预测值和实测值存在较大的误差。这是因为前者的实测数据中有5组数据参与网络的学习训练,而后者的实测数据中只有3组参与网络的学习训练,网络训练过程中由于参与学习训练的样本过少,从而造成了图7(b)中出现的预测情况。同时,这也进一步解释了表3中第3组测试数据在该模型中的预测误差较大的原因。

图7 不同H2S分压条件下腐蚀速率预测值与实测值对比Fig.7 Comparison between prediction and actual measurement of corrosion rate under different H2S pressure
2.2.7 CO2和H2S共存条件下对套管钢腐蚀速率的影响
设定温度为100℃,CO2分压分别为0.3,0.5,0.7,0.9,1.2,1.5,2.0 MPa,H2S分压分别为0.01,0.05,0.1,0.2,0.3,0.4,0.5,0.6 MPa,对所设定的两者分压条件利用遗传算法优化BP神经网络模型进行预测,一共得到56组预测数据,对预测结果进行整理,见图8。
由图8可见:H2S分压较高的区域腐蚀速率较

图8 基于遗传算法优化BP神经网络预测的腐蚀速率分布图Fig.8 The distribution picture of predicted corrosion rates of BP neural network optimized by genetic algorithm
低,而H2S分压较低时,随着CO2分压升高,腐蚀速率明显增加。分析CO2/H2S腐蚀机理时认为两者协同竞争条件下会出现腐蚀速率极大值,从此图中能够清楚地看出两者分压在一定区域范围内出现了腐蚀速率较大值,说明了此预测模型的可靠性很强。
3 结论
(1)鉴于BP神经网络本身具有一些不足之处,结合遗传算法优化BP神经网络再次进行预测,与单纯的BP神经网络模型预测相比,网络训练收敛速率有所增加,预测效果有所改善。
(2)利用建立的遗传算法优化BP神经网络模型分别对不同温度、不同CO2分压和不同H2S分压条件下的腐蚀速率进行预测,发现在CO2和H2S协同竞争腐蚀时由于腐蚀速率变化幅度较大和学习训练样本数据较少,导致该模型存在一定的预测误差。
[1] 周卫军,郭瑞,张勇.CO2分压对SM80SS套管钢在CO2/H2S共存环境中的高温高压腐蚀行为影响[J].全面腐蚀控制,2009,23(8):20-23.
[2] 张玉芳.H2S分压对SM80SS油管钢腐蚀行为的影响[J].腐蚀科学与防护技术,2007,19(4):290-292.
[3] 林学强,李效波,张海龙.温度对N80钢在CO2/O2共存环境中腐蚀行为的影响[J].腐蚀与防护,2014,35(1):56-59.
[4] 刘然克,张德平,郝文魁.H2S分压对N80油套管钢CO2环境下应力腐蚀开裂的影响[J].四川大学学报(工程科学版),2013,6:196-202.
[5] 张国安,陈长风,路民旭.油气田中CO2腐蚀的预测模型[J].中国腐蚀与防护学报,2005,25(2):119-123.
[6] 张继川,张双蕾,段蕴琦.天然气井腐蚀预测研究[J].钻采工艺,2012,35(3):86-88.
[7] 商杰,朱战立.基于遗传算法的神经网络在预测油管钢腐蚀速率中的应用[J].腐蚀科学与防护技术,2007(3):225-228.
[8] 李强,鞠虹,唐晓.基于人工神经网络的CO2/H2S腐蚀速率预测模型[J].腐蚀与防护,2013,1:10-12.
[9] 张清,李全安,文九巴.温度和压力对N80钢CO2/H2S腐蚀速率的影响[J].石油矿场机械,2004,33(3):42-44.
Application of Genetic Algorithms BP Neural Networks to Predicting Corrosion Rate of Carbon Steel in CO2/H2SEnvitonment
WAN Liping1,XU Youhong1,FENG Zhaoyang1,KONG Bin1,YANG Bin2
(1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,China;2.Machinery Plant Songyuan,Petroleum Administration Bureau Daqing,Songyuan 138000,China)
TG174
B
1005-748X(2017)09-0727-05
10.11973/fsyfh-201709014
2016-03-04
国家安监局科技项目(2016GJ-B3-041)
万里平(1972-),博士后,副研究员,主要从事欠平衡钻井、石油管材腐蚀与防护、油气田废水治理方面的研究,15928635619,wanliping72@sohu.com

