已实现类波动测算方法的比较与实证分析
,
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
已实现类波动测算方法的比较与实证分析
孙秋霞,冯佳伟
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
结合国内外研究新进展对金融高频数据波动率的特征进行综述,对比分析了已实现波动、已实现极差波动、已实现双幂次变差、偏差校正已实现双幂次变差、已实现极差四次幂变差等波动测算方法以及考虑日历效应对上述方法进行的赋权修正。从稳健性、有效性、无偏性等角度对已实现类波动的特征进行分析,并对上述成果建立HAR模型完成滚动预测和评价,最后指出赋权已实现极差四次幂变差为这十种高频数据波动率中最优的估计量。
已实现波动;日历效应;HAR模型;滚动预测
基于现代投资组合理论,方差常被用于衡量金融资产价格的不确定性,进而国内外学者对波动率开始深入研究,波动率现已成为金融资产风险度量、金融衍生品定价等方面的重要工具。波动率的测算方法主要分为三类:第一类是基于低频数据(日、周、月收益率)通过ARCH和SV族类模型测算得到的时变波动率,此类方法需要设定收益率序列服从某种分布,故亦称为参数法;第二类为通过倒推BS公式计算出的期权隐含波动率;第三类是高频数据的已实现类波动,Andersen等[1-5]首次提出以日内价格对数收益率的平方和作为真实波动的一致估计量,解决了ARCH类模型维数灾难问题,也不存在BS公式的强假设条件。
近年来ARCH模型的发展主要集中在刻画波动率的长记忆性、非对称性、从聚性等方面;关于隐含波动率的讨论,聚焦于修正假设与现实不符之处;对已实现波动的研究通过改进相关计量模型提高模型的预测精度;而少有学者基于市场真实波动率估计量,对已实现波动在无偏性、有效性、稳健性和日历效应角度的发展进行比较分析,实际上当资产价格存在跳跃和市场微观结构噪声影响下,已实现波动不再是真实波动的一致估计量,我们在此对已实现类波动理论进行系统梳理和实证分析:包括其适用范围、优缺点等,以期对不同市场结构已实现类波动的选择提供参考价值。
一、高频数据波动率测算方法的综述
本文综述内容包括如下10种高频数据波动率:已实现波动、已实现极差波动、已实现双幂次变差、偏差校正已实现双幂次变差和已实现极差四次幂变差,及考虑日内效应的赋权已实现波动、赋权已实现极差波动、赋权已实现双幂次变差、赋权偏差校正已实现双幂次变差和赋权已实现极差四次幂变差。
(一)已实现波动测算方法及其改进
1.已实现波动。Andersen等[5]利用二次变差理论在收益率序列满足零均值和无穷样本的条件下,证明已实现波动(Realized Volatility,简称“RV”)是积分波动(Integrated Volatility,简称“IV”)的无偏估计量。根据Andersen等最早提出的已实现波动率概念:第t天的日已实现波动RVt为日内高频收益率的平方和,即:
其中,yt(i)=100×(lnPt(i)-lnPt(i-1)),i=1,2,…,n
2.已实现双幂次变差。Barndorgg等[6]发现已实现波动不稳健的缺点,提出了更为稳健的已实现双幂次变差(Realized Bipower Variation,简称“RBV”),定义为:
其中,M表示一天内的抽样次数,h=1表示一天,yj,t表示第t天的第j个日内对数价格收益率。当r=0,s=2或者r=2,s=0时,RBVt=RVt,而且当r=s=1时的RBV优于已实现波动RV。
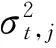
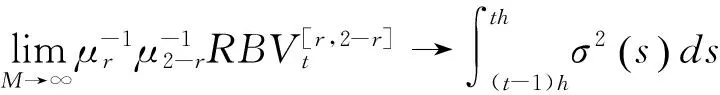
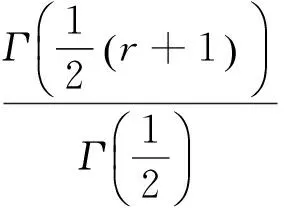
在此离散跳跃过程下,RV包含了跳跃项k2(u),此时的RV是有偏的,而RBV是可以消除这种跳跃带来的偏差。上式中可以看出在发生跳跃情况下,已实现双幂次变差依旧收敛于积分波动,然而已实现波动比积分波动多了跳跃项会导致结果偏大,所以已实现双幂次变差比已实现波动更为稳健。
3.偏差校正已实现双幂次变差。李胜歌等[8]克服已实现双幂次变差RBV受到微观结构噪声影响提出偏差修正的已实现双幂次变差,考虑到在r=s=1时的已实现双幂次变差比其他取值更加精确,在此基础上进行提出了偏差校正已实现双幂次变差(Bias Corrected Realized Bipower Variation,简称“BCRBV”),并用深圳成指不同抽样频率间隔数据实证表明BCRBV优于RBV,定义为:
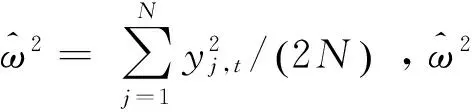
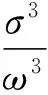
4.已实现极差波动。已实现极差波动是另一种计算思路为日内对数价格极差的平方和,由Christensen等[9]提出,估计积分波动(IV)更精确。所以在计算高频数据波动率方面RRV比RV更有效,已实现极差波动定义为:
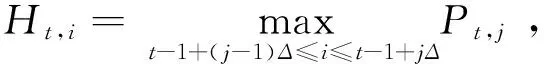
通过对比可以发现,已实现极差波动比已实现波动更具有一定的优势,主要体现在:
①已实现极差波动能够反映取样区间内所有的价格信息,而已实现波动仅考察区间两端点的价格,故已实现极差波动综合了更多日内价格的信息,更有利于估计真实波动率。
②唐勇等[10]53通过数学推导和使用上证综指1分钟数据进行实证,两方面都表明已实现极差波动比已实现波动更有效,Var(RRVt)≈Var(RVt)/5
5.已实现极差多幂次变差与已实现极差四次幂变差。Christensen和Podolskij[11]根据Barndorff-Nielsen[12]等人的多幂次变差思想,提出优于已实现多幂次变差的估计量-已实现极差多幂次变差(Realized Range-based Multipower Variation,简称为“RMV”),定义如下:
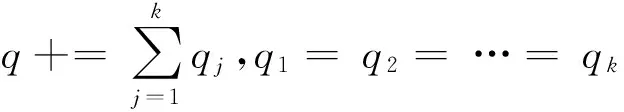
唐勇等[13]2766通过数值模拟的方法在k取值为1-4情况下得到幂次k=4时,已实现极差四次幂变差(Realized Range-based Quadpower Variation,简称“RQV”)在已实现极差二、三、四次幂变差族类波动中表现最好,并且用沪深300指数数据实证表明RQV优于RRV,定义如下:
高频数据波动率的“已实现”测算为非参数估计法,并不需要假定服从某个分布,拥有比低频数据更多的交易信息,但是会受到市场微观结构噪声和资产价格跳跃的影响,此时通过二次变差理论算得的高频波动不再是积分波动IV的一致估计量。上述五个波动中,①已实现波动与已实现极差波动受到微观结构噪声和跳跃影响,不再是一致估计量;②已实现双幂次变差在已实现波动基础上改进,故在资产价格存在跳跃时更为稳健;③偏差校正的已实现双幂次变差在已实现双幂次变差基础上克服了微观结构噪声的影响;④已实现极差四次幂变差在已实现极差波动基础上克服跳跃的影响。但从有效性角度看,极差的测算方法为抽样间隔内最高价减最低价,能反应更多的价格信息表现出方差更小的特征,故即便存在市场微观结构噪声和跳跃,已实现极差波动与已实现极差四次幂变差测算得到的波动率标准差最小。
(二)赋权已实现波动测算方法及其改进
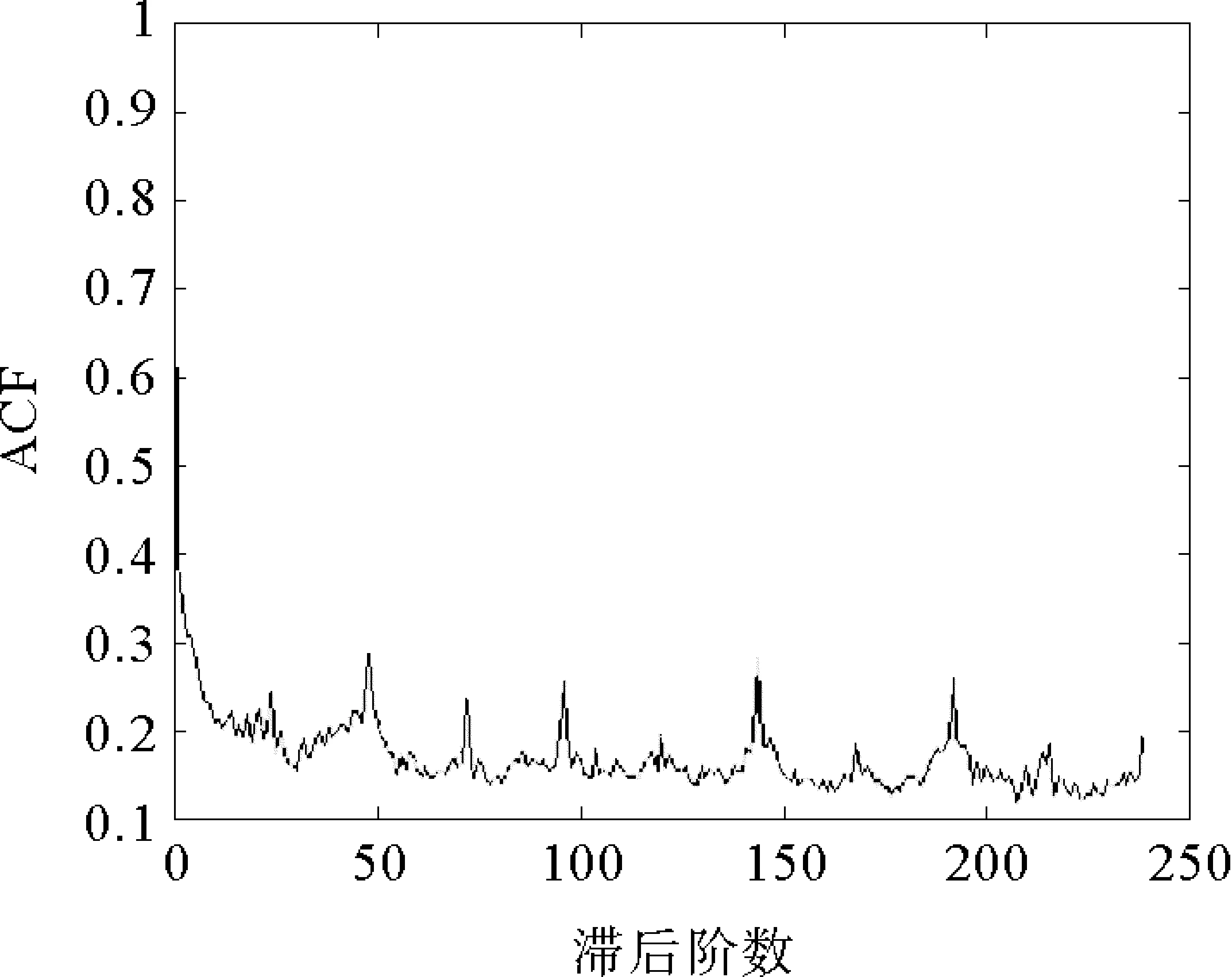
金融资产高频时间序列具有的一个重要特征是,其波动率的自相关函数(ACF)在日内呈现“U”型的变化模式。金融市场的波动情况在开盘和收盘的时候比较高,中间则较低,在这样的情况下必须通过对一天内的日内收益率平方赋予不同的权重以此来消除“日历效应”,有如下学者进行了研究。
1.赋权已实现波动
郭名媛等[14]通过改进已实现波动提出一种更为有效的度量方法-赋权已实现波动(Weighted Realized Volatility,简称“WRV”),即:
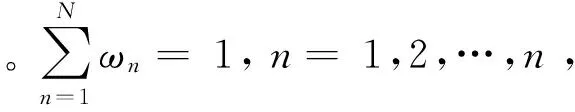
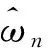
2.赋权已实现双幂次变差
李胜歌等[7]13对已实现双幂次变差进行改进提出赋权已实现双幂次变差(Weighted Realized Bipower Variation,简称“WRBV”),通过对上证综数和深证成指实证研究表明跳跃点上的RV>WRV>RBV>WRBV,WRBV和RBV更加稳健,故WRBV不仅具有RBV的稳健性以及对真实波动率的无偏性和有效性,同时解决了“日历效应”,定义如下:
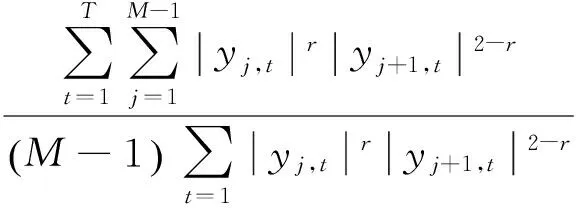
3.偏差校正的赋权已实现双幂次变差
李胜歌在其博士论文[15]中对偏差校正的已实现双幂次变差赋予不同权重消除了日历效应,赋权已实现双幂次变差(Bias Corrected Weighted Realized Bipower Variation,简称“BCRBV”)可以由下式来表示:
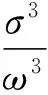
4.赋权已实现极差波动
唐勇,张世英[10]56在已实现极差波动基础上提出赋权已实现极差波动(Weighted Realized Range-based Volatility,简称“WRRV”)充分考虑了“日历效应”,用深圳成指5分钟、10分钟、15分钟、20分钟、30分钟、60分钟数据都验证了WRRV比RRV更有效,公式如下:
5.赋权已实现极差四次幂变差
唐勇,刘徽[13]2774不光证明了已实现极差四次幂变差在已实现极差多幂次变差中为最优的估计量,还对其进行了加权以消除日内偏斜“L”型模式,用沪深300指数10分钟证实了加权的已实现极差四次幂变差(Weighted Realized Range-based Quadpower Variation,简称“WRQV”)均值和标准差都最小、效果最好,WRQV 上述五种赋权已实现类波动分析如下:①权重确定均是根据无偏性和最小方差性求得,在这两个条件的约束下,无偏性可以保证真实波动率估计量的期望值等于积分波动率,最小方差性使得估计量的波动范围收敛于真值附近,并且相差很小。②赋权已实现类波动的权重计算公式具有相似性,分子为所有波动总和,分母为每天同一时刻波动合计,对于开盘和收盘的较大波动相当于被平滑了。表1给出了10种已实现类波动的特征性质比较:①计算方法上赋权的已实现类波动较无赋权已实现类波动更复杂,但可以做到更好的稳健性和有效性;②有效性方面赋权已实现极差四次幂变差最优,极差波动考虑了采样间隔内最高价和最低价能够反应更多的信息,相对于其他已实现类波动标准差更小,但其稳健性最差。 表1 “已实现”类波动特性比较 注:计算方法1-10表示复杂到简洁,稳健性1-10表示最优到最差,有效性1-10表示最优到最差。 (一)波动率的预测模型 本文选用Corsi[16]基于异质市场理论提出的(Heterogeneous Autoregressive)异质市场自回归模型,把高频数据波动率作为解释变量,通过加总不同交易者交易行为的影响可以刻画波动率的长记忆特征(自相关系数呈双曲率衰减)。 (1) (2) (3) 根据Müller等[17]创立的异质市场理论,从投资者的交易行为影响角度分析,表达式可以写成: (4) (5) (6) 把式(4)-(6)进行迭代,具体公式可表示为: (7) (二)预测评价 为了测算上文介绍的十种已实现类波动加入HAR模型的预测能力,本文采用了损失函数法与M-Z回归法两种方法进行评价。 1.损失函数法 损失函数法是一种传统的衡量模型预测能力的方法,且损失函数的值越小,说明预测越精确。本文采用两种常用损失函数:平均绝对误差(Mean Absolute Error,简称“MAE”)和均方根误差(RMSE,Root Mean Squared ErrorT,简称“RMSE”),其中: (8) 2.M-Z回归法 Mince-Zarnowitez回归法主要评价模型预测性的优劣,主要观察式(9)的拟合优度R2,R2越高表明模型预测越准确。 (9) Andersen等[4]权衡测量误差和微观结构噪声影响认为5分钟为最优采样频率,因此本文抽样间隔取为5分钟,且样本空间为:2014年3月6日—2016年3月10日上证综指的交易价格。剔除节假日后的交易天数为493天,这段时期共有48×493=23 664个数据,所使用的语言为Python和Matlab。 (一)日历效应与波动聚集特征 图1 5分钟日内极差RRV的自相关图 图1和图2的滞后阶数为240,日取样频率为48。如图1所见,已实现极差RRV的自相关函数(ACF)呈现出以“日”为周期的规律性“U”型变化,而加权后的已实现极差WRRV测算的结果显然已经消除其日历效应,不再呈现周期性变化(图2)。 图3中实线表示样本期间的上证综指日收盘价,虚线表示日已实现波动RVt。RVt时序图反映出金融高频数据的波动聚集特征,即大的波动发生后紧接着会出现大波动,小波动后接着小波动。通过日收盘价序列与RVt序列图趋势情况发现我国股市在2015年7、8月出现了显著的异常状况,波动幅度非常大。 图2 5分钟日内加权极差WRRV的自相关图 图3 日已实现波动RVt与上证综指日收盘价时序图 (二)已实现类波动测算结果的比较 本文选取的样本期间内中国股市经历了一场规模巨大的人造杠杆牛市,期间发生了三场大股灾令投资者损失惨重,根据行为金融学方面诺奖获得者丹尼尔·卡尼曼教授在其著作《思考,快与慢》[19]实证得到的投资者面对风险勇于激进冒险,面对收益选择保险谨慎的结论,上述情况下存在投资者更愿意在下跌中博反弹、2015年6月中旬开始的融资盘强平以及“国家队”的救市,这三种效应放大了暴跌期间股市的波动,根据上文提到的跳跃扩散过程理论显然在价格出现大幅度跳跃时,RV不再是积分波动的一致估计量,包括了跳跃项故会导致偏大[20,21]。为了便于比较,进行把样本区间细分为稳定期(2014年3月6日-2014年6月);暴涨期(2014年7月-2015年6月12日);暴跌期1(2015年6月15日-2015年9月30日);恢复期1(2015年10月-2015年12月);暴跌期2(2016年1月-2016年1月31日)。 通过表2可以发现:①RV等已实现类波动在稳定期间均值和标准差差距并不大,在所有不同期间中最为稳定准确,稳定期价格是服从连续扩散过程,进行波动率测算时可以选取较为计算方便的波动;②暴涨期间为牛市开始到结束,已实现类波动的均值和标准差有明显的增大,BCRBV、WBCRBV偏差修正的改进实证只是略优于RV、WRV、RBV、WRBV,而包含采样区间内信息更多RRV、WRRV、RQV、WRQV更为稳健;③暴跌期1的波动统计特征达到了最大,这也证实了下跌期间负的收益冲击对波动的影响更大(高频数据波动的不对称特征)。期间两轮大股灾(7月初、8月初)原因为2015年6月中旬证监会开始清理场外配资多米诺骨牌效应连锁放大、股票资产本身的高估值向均值的回归过程,以及这期间“国家队”向银行融资借款直接买入股票,股价有从跌停板拉升到涨停,导致了股票市场的状况变得极端异常,波动幅度大与发生次数多甚至超过了2008年金融危机期间,该期间价格服从跳跃扩散过程,RRV、WRRV、RQV、WRQV明显优于其他已实现类波动,关于极差的波动有效性最优占据着绝对优势;④恢复期1股市经历了三个月的上涨反弹幅度可观,已实现类波动的均值与标准差较为明显下降,在均值方面差距并不十分显著;⑤暴跌期2,2016年初开设的熔断机制到叫停短短4日,频繁触发熔断阀值股票、期货停止交易,由于熔断机制的磁吸效应与股票上涨的反弹结束,期间发生了股灾3.0,已实现类波动的均值标准差增大较为明显,RRV、WRRV、RQV、WRQ统计特征比较相近,WRQV与RQV克服了跳跃影响,在两次暴跌中标准差均为最小,该期间选用这几种已实现类波动进行定价、风险管理合适。 表3 5分钟抽样频率下波动估计量的描述性统计特征 (三)模型预测效果比较 采用滚动时间窗口法进行样本外预测,训练期为373天,验证期为101天,保持373天的长度不变,进行建模并代入数据预测下一天,循环以步长为1天向前滚动,最终将模型预测值与验证期的真实值进行比较评价。 表4 不同已实现类波动模型的预测效果评价 注:M1表示HAR-lnRV模型,M2表示HAR-lnWRV模型,M3表示HAR-lnRBV模型,M4表示HAR-lnWRBV模型,M5表示HAR-lnBCRBV模型,M6表示HAR-lnWBCRBV模型,M7表示HAR-lnRRV模型,M8表示HAR-lnWRRV模型,M9表示HAR-lnRQV模型,M10表示HAR-lnWRQV模型。 从表4中可以看出,①M-Z回归法测得的HAR-lnRV类模型拟合优度R2均在0.3左右,说明了线性模型在刻画非线性的金融市场方面存在些许不足,样本期间股票价格的大幅度跳跃现象也表现出了非线性特征,已实现极差四次幂变差模型的拟合优度最高,受跳跃的影响最小。②从MAE和RMSE两种损失函数计算结果看,赋权已实现类波动的评价值均小于无赋权已实现类波动,表明波动经过赋权后标准差减小、预测精度更高。③受熔断机制影响,2016年1月7日的RQV和WRQV计算结果为0,将该异常值视为缺失值处理,运用HAR模型回归预测进行插补,造成M10的MAE结果大于M9,其余评价指标正常。④由于文章篇幅限制选取常用的日已实现波动RVt与RRVt的预测图,图4和图5可以看出,对于大的波动模型难以捕捉,建立合适的波动率预测模型是时间序列建模者的下一步挑战。 图4 RVt预测值vs RVt真实值 图5 RRVt预测值vs RRVt真实值 [1]ANDERSON T G,BOLLERSLEV T.Answering the skeptics:yes,standard volatility models do provide accurate forecasts[J].International Economic Review,1998(4):885-905. [2]ANDERSON T G,BOLLERSLEV T,DIEBOLD F X,etal.Exchange rate returns standardized by realized volatility are (nearly)gaussian[J].Multinational Finance Journal,2000(4):159-179. [3]ANDERSON T G,BOLLERSLEV T,DIEBOLD F X,etal.The distribution of exchange rate volatility[J].Journal of American Statistical Association,2001(96):42-55. [4]ANDERSON T G,BOLLERSLEV T,DIEBOLD F X,etal.The distribution of realized stock return volatility[J].Journal of Financial Economics,2001(5):43-76. [5]ANDERSON T G,BOLLERSLEV T,DIEBOLD F X,etal.Modeling and forecasting realized volatility [J].Econometrica,2003(2):579-625. [6]BARNORFF-NIELSEN O E,SHEPHARD N.Power and bipower variation with stochastic volatility and jumps[J].Journal of Financial Econometrics,2004(1):1-37. [7]李胜歌,张世英.金融波动的赋权“已实现”双幂次变差及其应用[J].中国管理科学,2007(5). [8]李胜歌,张世英.金融高频数据的偏差校正“已实现”双幂次变差[J].系统工程学报,2008(4):392-397. [9]CHRISTENSEN K,PODOLSKIJ M.Asymptotic theory for range-based estimation of integrated variance of a continuous semi-martingale[R].Aarhus School of Business,2005. [10]唐勇,张世英.高频数据的加权已实现极差波动及实证分析[J].系统工程,2006(8). [11]CHRISTENSEN K,PODOLSKIJ M.Asymptotic theory of range-based multipower variation[J].Journal of Financial Econometrics,2012(3):417-456. [12]BARNORFF-NIELSEN O E,SHEPHARD N.Variation,jumps,market frictions and high frequency data in financial econometrics[C]//Advances in Economics and Econometrics:Theory and Applications,Ninth World Congress,2007,3:328-372. [13]唐勇,刘微.加权已实现极差四次幂变差分析及其应用[J].系统工程理论与实践,2013(11). [14]郭名媛,张世英.赋权已实现波动及其长记性,最优频率选择[J].系统工程学报,2006(6):568-573. [15]李胜歌.基于高频数据的金融波动率研究[D].天津:天津大学,2008:1. [16]CORSI F.A simple approximate long-memory model of realized volatility[J].Journal of Financial Econometrics,2009(2):174-196,2009. [17]MULLER et al.Fractals and intrinsic time-a challenge to econometricians[J].The International AEA Conference on Real Time Econometrics,1993(5),14-15. [18]西村有作.基于高频数据的中国股市波动率研究[M].北京:对外经济贸易大学出版社.2014. [19]丹尼尔·卡尼曼.思考,快与慢[M].北京:中信出版集团股份有限公司,2012. [20]李彩云.“已实现”跳跃检验与跳跃风险测度[D].武汉:华中科技大学,2013:6. [21]王凤华,贾俊艳,等.基于加权已实现极差的中国股市波动特征[J].系统工程,2011(9):66-71. ComparisonandEmpiricalAnalysisofMeasurementMethodsofRealizedVolatility SUN Qiuxia, FENG Jiawei (CollegeofMathematicsandSystemsScience,ShandongUniversityofScienceandTechnology,Qingdao266590,China) The paper summarizes the characteristics of the volatility of high frequency data of the domestic and foreign research progress, and conducts a comparative analysis of fluctuation measuring methods, such as realized volatility, realized range-based volatility, realized bi-power variation, bias-corrected realized bi-power variation, realized range-based quad-power variation, considering the weighted correction given by calendar effect to the above methods. From the perspective of robustness, effectiveness and non bias, the characteristics of the realized fluctuation have been analyzed, and the HAR model is established to complete the rolling prediction and evaluation. Finally, it is pointed out that realized range-based qua-dpower variation is the best estimate of the ten kinds of high frequency data volatility. realized volatility;calendar effect;HAR model;rolling prediction F830 A 1008-7699(2017)05-0078-10 (责任编辑魏霄) 2017-1-14 山东科技大学科研创新团队支持计划资助项目(2015TDJH103);青岛市知识产权软科学研究计划项目(QDISSP-1305) 孙秋霞(1976—),女,山东济宁人,山东科技大学数学与系统科学学院副教授,博士,博士后,硕士生导师;冯佳伟(1993—),男,上海松江人,山东科技大学数学与系统科学学院硕士研究生,本文通信作者.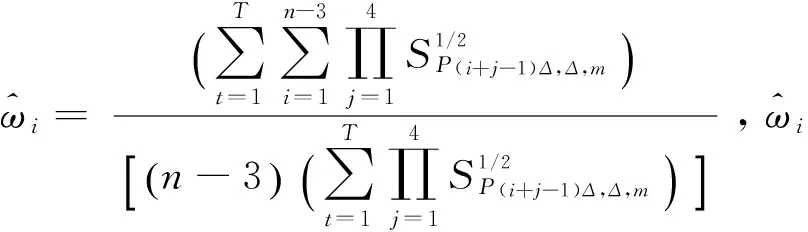

二、波动率的预测模型及其评价方法
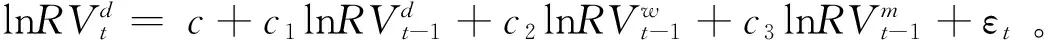
三、实证分析






四、结语