基于快速终端滑模算法的机械手跟踪控制研究
钱东海 黄友昕 董小康 吴 鹏
上海大学机电工程与自动化学院,上海,200072
基于快速终端滑模算法的机械手跟踪控制研究
钱东海 黄友昕 董小康 吴 鹏
上海大学机电工程与自动化学院,上海,200072
提出了一种模糊自适应快速终端滑模控制方法。该控制方法采用多幂次趋近律构造趋近运动,用以提高趋近滑模面的速度,然后对常规的终端滑模面进行改进,提高沿滑模面收敛的速度。为消除控制系统中存在的不确定因素和建模误差,该控制算法还引进模糊自适应方法进行在线逼近。利用李雅普诺夫定理证明了所提出算法的稳定性。最后基于MATLAB与ADAMS联合仿真平台,采用所提出的算法对自行设计的3R型机械手进行轨迹跟踪研究,仿真结果显示,本控制方法具有更快的收敛性和更强的鲁棒性,有效地抑制了滑模控制中存在的振荡。
模糊自适应;快速终端;非奇异终端;机械手控制;联合仿真
0 引言
近年来,多关节机器人智能控制越来越得到人们的关注。多关节机器人是一种十分复杂的多输入多输出的非线性系统,具有耦合、时变、非线性等多种动力学特征,并具有一定的不确定性,因此,模糊控制、自适应控制、滑模变结构控制[1]等智能算法广泛用于多关节机器人控制中。
滑模变结构控制过程分为趋近滑模面阶段和沿滑模面运动阶段。为提高轨迹跟踪速度,需要针对性地减少这两个阶段的时间。文献[2]通过模糊滑模面以减少趋近阶段的时间,但这增加了沿滑模面运动的时间。文献[3]设计了一种多幂次的趋近律,保证了在远离滑模面和趋近滑模面相对较快的趋近速度,但系统中存在的不确定项无法准确地得到。
在沿滑模面运动阶段,由于传统滑模变结构控制的误差以指数级趋于零,故其误差不能在有限时间内趋于零。终端滑模[4]能够解决这一问题,误差可以在有限时间内收敛为零,但若沿滑模面运动的误差较大时,终端滑模速度反而小于传统滑模,同时,终端滑模在平衡点上存在奇异性,这将导致计算出的控制器输出趋于无穷大。可通过增加状态变量高阶项[5],加快误差较大时终端滑模沿滑模面收敛的速度,同时可通过改进滑模面[6],避免终端滑模的奇异性。
对于系统的建模误差和不确定性,传统滑模控制通过引入符号函数来保证系统的稳定性,但由于符号函数的不连续,导致输入力矩振荡。上界(滑模增益)越大,振荡越强烈。为消除振荡,文献[7]通过引入振荡程度系数,并采用模糊控制,来减小振荡。文献[8-11]通过模糊控制、自适应控制、神经网络相互结合的方法对整个系统或不确定项进行逼近,消除不连续项,从而减小振荡。文献[12]对切换函数进行改进以消除振荡。
本文提出一种模糊自适应快速终端滑模控制方法,该方法采用多幂次趋近律提高趋近滑模面的速度,采用快速终端滑模面提高沿滑模面收敛速度;为消除系统中存在的不确定因素,该方法采用模糊自适应的方法对不确定项进行逼近。
1 3R型腕部结构
1.1机械结构
3R型腕部结构[13]如图1所示,包含三个旋转副(revolute),四个杆件。从机器人学角度划分,包括连杆0、连杆1、连杆2和连杆3(法兰盘)。连杆0固定,连杆1相对于连杆0的转动构成关节1,连杆2的相对于连杆1的转动构成关节2,连杆3(法兰盘)的相对于连杆2的转动构成关节3。关节1、关节2和关节3回转轴的轴线两两垂直,且第三个转动自由度的回转轴线与第一个转动自由度、第二个转动自由度的回转轴线相交,不存在偏置。
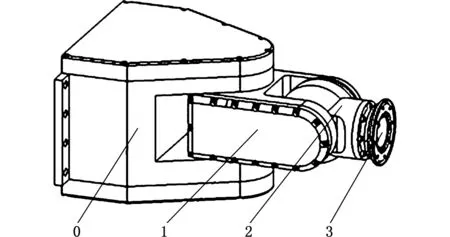
图1 3R型腕部结构Fig.1 3R wrist structure
1.2动力学模型
定义q=[q1q2q3]T为各关节的关节变量,τ=[τ1τ2τ3]T为各关节驱动力矩,其动力学方程[14]为
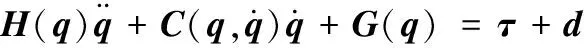
(1)
(2)
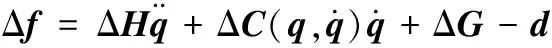
(3)

1.3MATLAB与ADAMS联合仿真
将3R型机械手在Solidworks中建模,导入ADAMS。在ADAMS中,对模型进行简化,设置运动副,定义输入变量、输出变量、质量等参数,最后在ADAMS中生成MATLAB中可以使用的模块。
2 非奇异快速终端滑模控制
2.1快速镇定问题
终端滑模分为趋近阶段和沿滑模面运动阶段,提高这两个阶段的收敛速度可以提高终端滑模的收敛速度。趋近阶段可以看成滑模面si的镇定问题,沿滑模面运动阶段可以看成误差ei的镇定问题。
微分方程:
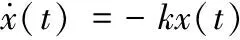
(4)
(5)
(6)
k>0 0
为消除复数运算,令sgna(x(t))=sgn(x(t))|x(t)|a。
式(4)的解为x(t)=x0e-kt,x需要t→∞才能趋于0。式(5)需要有限时间能使x趋于0,式(6)中x需要t→∞才能趋于0。
所以取

(7)
0
这能在有限时间内使x(t)更快地趋于0。
2.2快速终端滑模面的设计
滑模面可设计为
(8)
0
但是以此滑模面设计控制率时,输入项中包含|e|a-1,当e=0时,此项无穷大,造成奇异性。
为避免奇异性,并保证滑模的快速性,将滑模面改为
(9)

(10)
对于3R型腕部结构,滑模面S为一向量:

(11)
γ1=diag(γ11,γ12,γ13)
(12)
γ2=diag(γ21,γ22,γ23)
(13)
A=diag(α1,α2,α3)
(14)
B=diag(β1,β2,β3)
(15)
sgnA-I(e)=diag(sgnα1-1(e1),sgnα2-1(e2),
sgnα3-1(e3))
(16)
其中,S=[s1s2s3]T;γ1i>0,γ2i>0,1<βi<2,αi>βi,i=1,2,3;I为单位矩阵。
2.3趋近滑模面运动的趋近律的设计
由于趋近律不存在避免奇异性问题,故趋近律可设计成
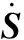
(17)
其中,M=diag(m1,m2,m3),N=diag(n1,n2,n3),0
2.4控制率设计
由式(2),取控制率
τ=τ1+τ2+τ3+τ4+τ5
(18)
其中,τ1、τ2、τ3为关于快速终端滑模的控制器设计输出,τ4、τ5为模糊自适应的控制器设计输出,用于趋近Δf,将在下文介绍。
τ1~τ3的表达式为
(19)

(20)

(21)
3 模糊自适应控制
3.1模糊趋近
以S=[s1s2s3]T作为输入,通过If-Then模糊规则对Δf进行估计。第r条模糊规则为

ThenyrisOr
r=1,2,…,nr
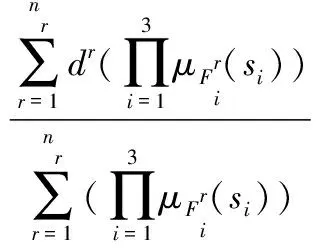
(22)
其中,dr是各个隶属函数为1时的值。y(S)也可以表示为
y(S)=ξTθ
(23)
其中,θ=[d1…dr…dnr]T为系数向量,通过自适应进行逼近最优参数,ξ=[ξ1…ξr…ξnr]T为回归向量,定义ξr:
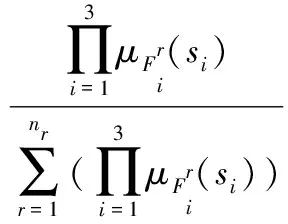
(24)
3.2自适应模糊控制
用于逼近Δf的自适应模糊向量为
其中,
(25)
(26)


(27)
(28)
εf(S)=[εf1(S)εf2(S)εf3(S)]T
(29)
(30)
(31)

(32)
τ5是针对自适应模糊控制保证稳定性的鲁棒项。定义σ0是一个正常数,小于(H0(q))-1的最小特征值,则τ5为
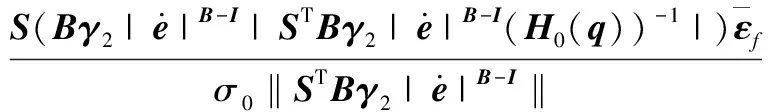
(33)
3.3稳定性验证
取Lyapunov函数为
(34)
(35)
由式(11)得
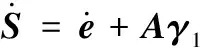
(36)
将式(18)~式(21)、式(26)、式(33)代入式(2),化简得
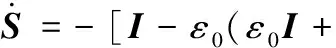
(37)
(38)
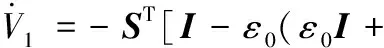
(39)
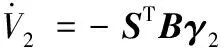
(40)

(41)


STΛH0(q)-1SΛ≥σ0‖STΛ‖
(42)
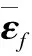
(43)
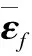
(44)
4 仿真实验
仿真实验采用上文所介绍的3R型机械结构进行轨迹跟踪,模糊自适应快速终端滑模参数如下:
qd=[0.5+sin2πt0.5+sin2πt0.5+sin2πt]
γ1=diag(1,1,1)
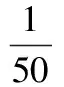
A=diag(9,9,9)
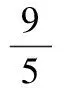

N=diag(5,5,5)
K3=K4=diag(60,60,60)
轨迹跟踪结果如图2所示,可以看出,在0.3~0.5 s,三个关节实际轨迹收敛于理想轨迹。
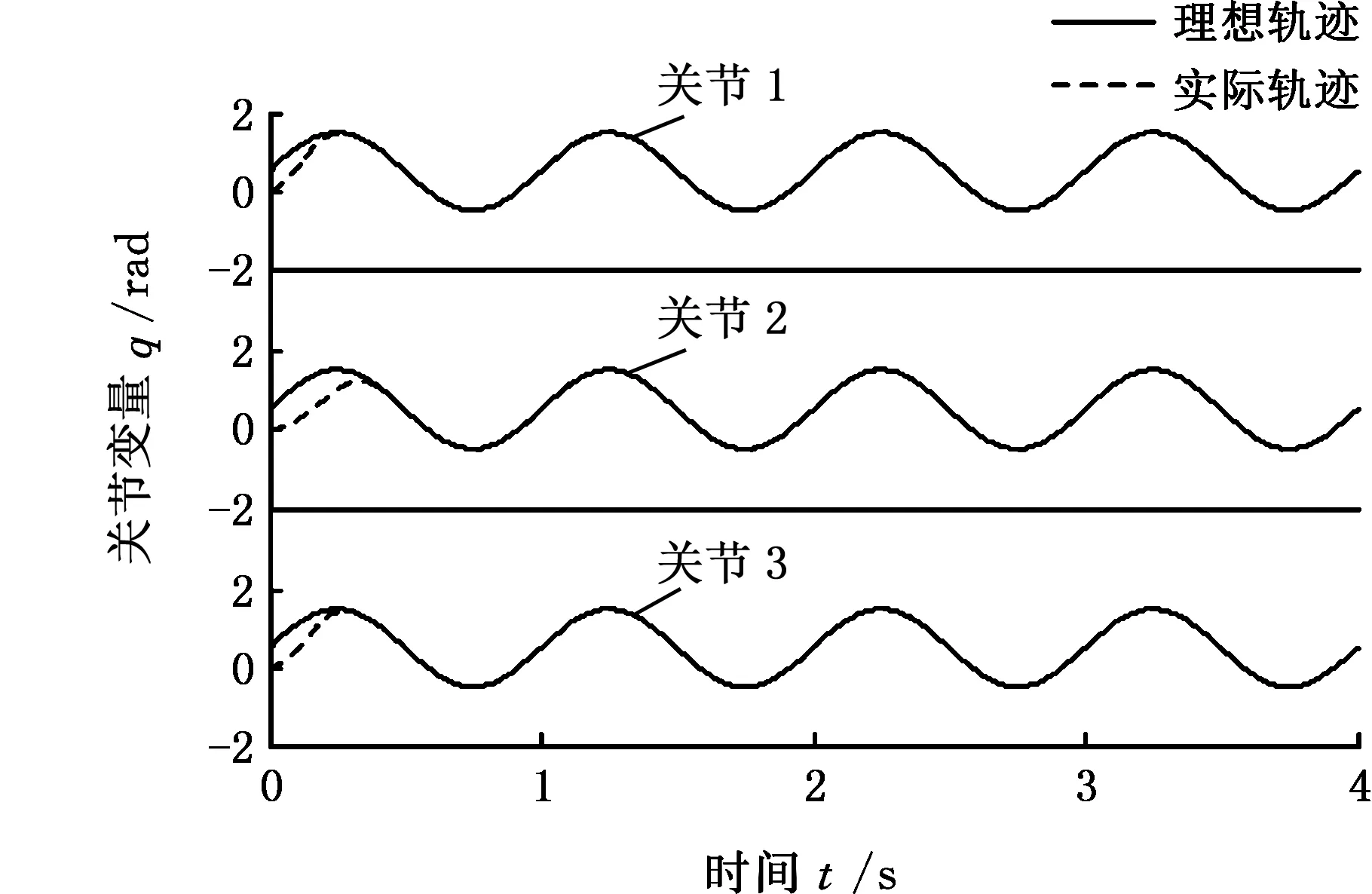
图2 模糊自适应快速终端滑模轨迹跟踪Fig.2 Position tracking of fuzzy adaptive fast terminal sliding mode
同时,将模糊自适应快速终端滑模控制方法与传统滑模变结构方法相比较,误差比较结果如图3所示,可以看出,模糊自适应快速终端滑模控制方法的收敛速度明显优于传统滑模变结构收敛速度。

图3 误差比较Fig.3 Error comparison
输入力矩比较结果如图4所示,可以看出,传统滑模变结构的输入力矩有很强的振荡,而使用模糊自适应的方法对不确定项进行逼近,振荡明显减弱。
5 结论
本文针对传统滑模收敛速度慢且终端滑模存在奇异性的不足,设计了一种非奇异性快速终端滑模控制算法,并针对滑模控制中存在的振荡,采用模糊自适应方法对不确定项进行逼近,从而减轻振荡。同时,对算法的稳定性进行了证明,并通过MATLAB与ADAMS联合仿真对本控制方法的有效性、快速性进行了验证,结果表明,该方法具有更快的收敛速度和更小的输入振荡。
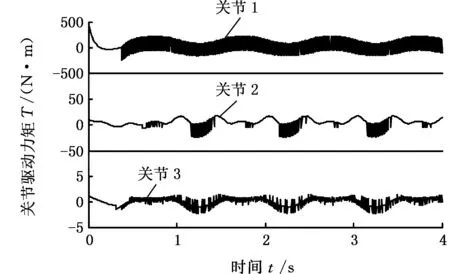
(a)传统滑模变结构
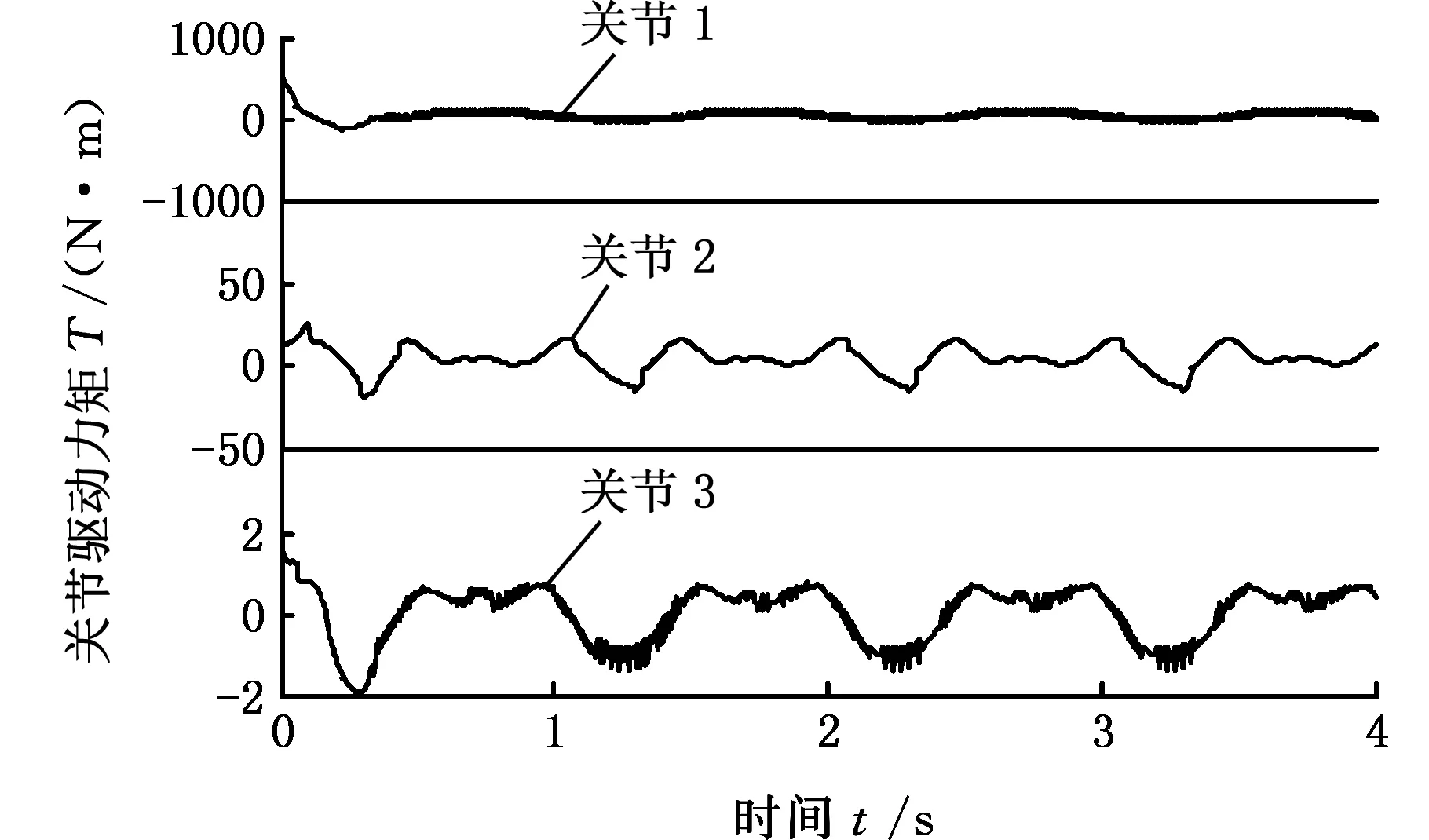
(b)模糊自适应快速终端滑模图4 输入力矩Fig.4 Input torque
[1] HE J, LUO M, ZHANG Q, et al. Adaptive Fuzzy Sliding Mode Controller with Nonlinear Observer for Redundant Manipulators Handling Varying External Force[J]. Journal of Bionic Engineering, 2016, 13(4):600-611.[2] NURKAN Y,YUKSEL H. Robust Control of a Spatial Robot Using Fuzzy Sliding Modes[J]. Mathematical and Computer Modelling.2009,49:114-127.
[3] 张瑶,马广富,郭延宁,等.一种多幂次滑模趋近律设计与分析[J].自动化学报,2016,42(3):466-472. ZHANG Yao, MA Guangfu, GUO Yanning, et al. A Multi Power Reaching Law of Sliding Mode Control Design and Analysis[J]. ACTA Automatica Sinica, 2016, 42(3):466-472.
[4] XIONG J, GAN Q, Ren W. Boundedness of Discretised Non-linear Systems under Fast Terminal Sliding Mode Control[J]. IET Control Theory & Applications,2016,10(16): 2100-2109.
[5] YANG Liang, YANG Jianying. Nonsingular Fast Terminal Sliding-mode Control for Nonlinear Dynamical Systems[J].Int.J.Robust.Nonlinear Control, 2011,21:1865-1879.
[6] MAO Z, ZHENG M, ZHANG Y. Nonsingular Fast Terminal Sliding Mode Control of Permanent Magnet Linear Motors[C]//Chinese Control and Decision Conference. Yinchuan, 2016:649-653.
[7] ABDELHAMEED M M. Enhancement of Sliding Mode Controller by Fuzzy Logic with Application to
Robotic Manipulators[J]. Mechatronics,2005,15: 439-458.
[8] SALEM M, KHELFI M F. Online RBF and Fuzzy Based Sliding Mode Control of Robot Manipulator[C]//International Conference on Sciences of Electronics,Technologies of Information and Telecommunications, IEEE. Sosse, Tunisia, 2012:896-901.
[9] NEKOUKAR V, ERFANIAN A. Adaptive Fuzzy Terminal Sliding Mode Control for a Class of MIMO Uncertain Nonlinear Systems[J].Fuzzy Sets and Systems,2011,179:34-49.
[10] LIU Haitao, ZHANG Tie. Adaptive Neural Network Finite-time Control for Uncertain Robotic Manipulators[J]. J. Intell. Robot Syst., 2014,75:363-377.
[11] XIA K, GAO H, DING L, et al. Trajectory Tracking Control of Wheeled Mobile Manipulator Based on Fuzzy Neural Network and Extended Kalman Filtering[J]. Neural Computing & Applications, 2016,10:1-16.
[12] 常雪剑, 刘凌, 崔荣鑫,等. 永磁同步电机非奇异快速终端可变边界层滑模控制[J]. 西安交通大学学报, 2015, 49(6):53-59. CHANG Xuejian, LIU Ling, CUI Rongxin, et al. A Nonsingular Fast Terminal Sliding Mode Controller with Varying Boundary Layers for Permanent Magnet Synchronous Motors[J]. Journal of Xi’an Jiaotong University, 2015, 49(6):53-59.
[13] 钱其超,钱东海,黄友昕,等. 一种用于直角坐标机器人的新型腕部结构[J].制造业自动化,2015,37(12):67-69. QIAN Qichao, QIAN Donghai, Huang Youxin, et al. A New Robot Wrist Structure Especially for Cartesian Robot[J]. Manufacturing Automation, 2015, 37(12):67-69.
[14] 霍伟.机器人动力学与控制[M].北京:高等教育出版社, 2005. HUO Wei. Robot Dynamics and Control[M]. Beijing: Higher Education Press, 2005
(编辑郭伟)
ResearchonTrackingControlforRobotManipulatorBasedonFastTerminalSlidingModeMethod
QIAN Donghai HUANG Youxin DONG Xiaokang WU Peng
School of Mechatronic Engineering and Automation,Shanghai University,Shanghai,200072
An adaptive fuzzy fast terminal sliding mode control method was proposed herein.In order to improve the the convergence speed,this method usd a multi power reaching law combind with fast terminal sliding-mode control. Adaptive fuzzy method was employed to approximate to the uncertain factor in the system of robotic manipulators. The system stability was proved by Lyapunov principle.The co-simulation of the 3R robotic maniputlators which was desined by authors was performed based on ADAMS and MATLAB. It turns out that the method has better convergence,and enhances robustness and reduces chatter.
adaptive fuzzy; fast teminal slide; nonsingular terminal slide; manipulator control; co-simulation
2016-10-18
TP273
10.3969/j.issn.1004-132X.2017.18.014
钱东海,男,1971年生。上海大学机电工程与自动化学院副教授。研究方向为机器人控制、计算机视觉、最优化方法、机器人及物流自动化应用。发表论文约40篇,获中国专利30项。E-mail:dhqian@126.com。黄友昕,男,1992年生。上海大学机电工程与自动化学院硕士研究生。董小康,男,1992年生。上海大学机电工程与自动化学院硕士研究生。吴鹏,男,1991年生。上海大学机电工程与自动化学院硕士研究生。

