数值模拟碳纳米管增强铝基复合材料的力学性能

，， ，

(1.东北大学 机械工程学院，辽宁 沈阳 110000； 2.沈阳理工大学 机械工程学院，辽宁 沈阳 110000)

数值模拟碳纳米管增强铝基复合材料的力学性能

赵磊磊1，邓永胜1，周丽2，李德治1

(1.东北大学机械工程学院，辽宁沈阳110000；2.沈阳理工大学机械工程学院，辽宁沈阳110000)

本文根据连续介质理论，采用代表性体积元的方法计算了碳纳米管增强铝基复合材料的力学性能。使用有限元软件ABAQUS对代表性体积元模型进行分析，研究了不同碳纳米管体积分数对复合材料弹性模量、屈服强度、泊松比及剪切模量的影响。结果表明碳纳米管体积分数对复合材料力学性能有显著影响，随着碳纳米管体积分数的增加，复合材料的弹性模量、屈服强度及剪切强度都明显提高，泊松比略有下降。

碳纳米管铝基复合材料； 代表性体积元； 力学性能； 有限元

1 引 言

碳纳米管增强铝基复合材料具有质量轻、比强度高、抗疲劳性能好、韧性好、抗冲击性高、耐高温耐磨损等优点[1-4]，已经成为航空航天及其他尖端技术领域重要的高性能材料。20世纪90年代，Kuzumaki[5]等人首次通过简单粉末混合然后进行热压、热挤等工艺制备出碳纳米管增强铝基复合材料，并对复合材料的力学性能进行了测试，结果表明碳纳米管对铝基体力学性能的提高有显著影响。目前，研究人员不断地对碳纳米管增强金属基复合材料制备方法的不断探索，其制备方法主要包括粉末冶金法、熔炼法、喷涂法、化学沉积法等[6]。其中，粉末冶金法工艺简单，对设备要求不高，成为制备碳纳米管增强铝基复合材料的常用方法[7-8]。Esawi[9]等人运用此方法制备出质量分数为2%的CNTs/Al基复合材料，其拉伸强度达到345MPa，比铝基体强度提高了21%。

运用连续介质理论研究微观问题已经取得了巨大的进步[10]，而且连续介质模型已经成功地用于模拟碳纳米管的力学性能，很多计算结果都得到了实验和分子动力学方法的验证，成为研究碳纳米管的重要工具，使得碳纳米管增强复合材料的研究取得了较大的进展。田文龙[11]等人根据连续介质理论，采用随机序列吸收算法产生高体积分数的碳纳米管增强铝基复合材料代表性体积元，运用有限元方法对高体积分数的代表性体积元进行了数值模拟。结果表明，随着碳纳米管体积分数的增加，复合材料的杨氏模量和剪切模量逐渐增加，泊松比逐渐减小。

直至目前，对碳纳米管增强铝基复合材料的研究仍大部分采用实验方法测定复合材料的力学性能，再与铝基体材料做比较[12]，而且碳纳米管的体积分数较低。虽然也有用数值模拟的方法建立较高体积分数的碳纳米管增强铝基复合材料的模型，但其碳纳米管的长度都是短碳纳米管，因此不能充分全面地模拟碳纳米管增强铝基复合材料的性能。本文采用代表性体积元的方法，建立了长碳管高体积分数的碳纳米管增强铝基复合材料的模型，并使用有限元软件对该模型进行模拟分析。

2 不同体积分数的碳纳米管增强铝基复合材料模型的建立

2.1代表性体积元几何模型的建立

复合材料的增强体在基体内具有统计学上的周期性，研究人员为了研究方便提出了复合材料在微观结构上具有周期性的假设[13]。代表性体积元是从复合材料上隔离出的具有代表性的单元，包含了复合材料所有理化性能和力学性能的最小体积单元，复合材料是由这个单元周期性排列构成[11]。当对复合材料施加外载荷时，因为所有的代表性体积元都是相同的，它们表现出相似的理化反应和力学反应，因此可以通过分析一个代表性体积元来预测复合材料的性能。

代表性体积元模型是由一系列中空碳纳米管随机镶嵌在2024铝合金基体中构成的，模型中的碳纳米管互不相交。为了研究不同的碳纳米管体积分数对铝基体的影响，代表性体积元的体积VRVE不变，通过改变碳纳米管的个数N来改变碳纳米管所占基体的体积分数Vf。代表性体积元的形状是一个立方体，其尺寸为400×400×400nm3。根据文献研究[14]，碳纳米管是由单层或多层石墨片卷曲而成的无缝纳米管状壳层结构，相邻层间距与石墨的层间间距相当，约为0.34nm。碳纳米管的直径为零点几纳米至几十纳米不等，长度一般为几十纳米至微米级，也有超长的碳纳米管，长度达2mm[16-17]，本文碳纳米管的外径取d=30nm，厚度t=2nm，长度L=300nm。不同体积分数的碳纳米管的根数N由式(1)得出：

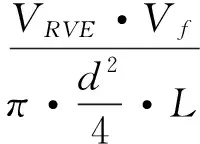
(1)

为了使代表性体积元的模拟效果更接近实际情况，在代表性体积元界面附近的中空碳纳米管被边界面切断时，应该将其移动到该边界面的对面，这样当代表性体积元重复复制构成复合材料时，边界面附近的碳纳米管还能完整地拼接出来，具体说明见图1所示。

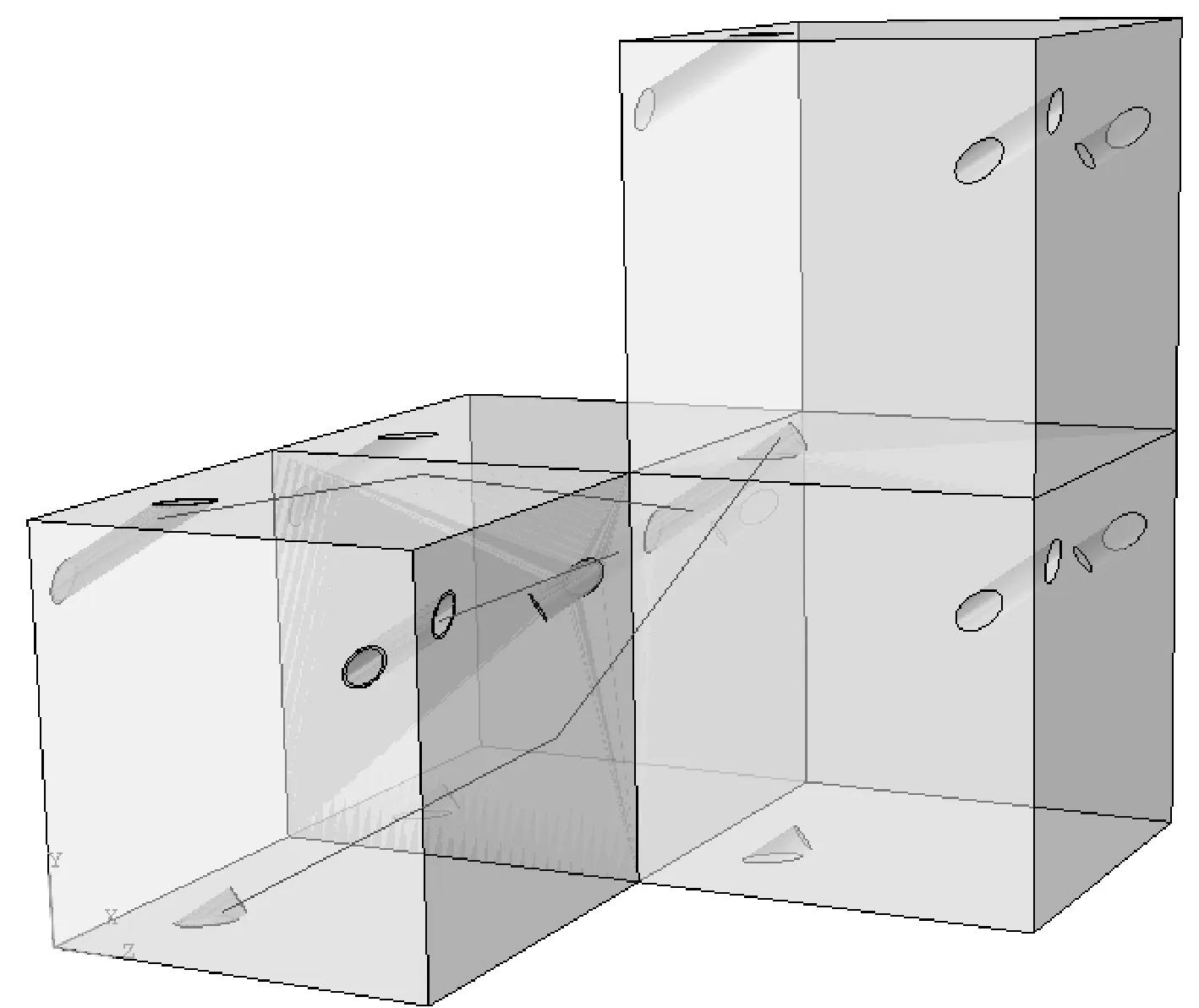
图1 代表性体积元边界面附近的CNT分布图Fig.1 CNT distribution near the edge of the representative volume element

2.2代表性体积元模型的材料

本文复合材料基体采用2024铝合金，系高强硬铝合金，具有强度高、耐热性好、成型优良及耐损伤等特点[15]，是航空航天、轨道交通等高新技术产业的主要结构材料。其力学性能如表1所示。

表1 2024铝合金力学性能

根据张振华等人[18]对碳纳米管弹性模量的测量，碳纳米管的杨氏模量范围0.9～1.14TPa，本文取1TPa，根据Shintani.K等人[19]对碳纳米管泊松比的测量，碳纳米管的泊松比取值范围为0.05～0.28，本文取0.2。

2.3代表性体积元的有限元模型

将在ABAQUS软件part模块创建的几何模型导入到mesh模块生成有限元模型。为了避免铝基体和碳纳米管增强体网格节点啮合不好的问题，铝基体和碳纳米管的网格类型均采用四面体单元。为了使模拟结果更加正确，不同体积分数的基体网格密度都相同。网格密度的选取原则是尽可能地减少不规则的单元同时兼顾铝基体网格密度与碳纳米管网格密度相当。在模型复杂的地方使用较密的局部网格密度以提高划分网格的质量，使计算结果更加正确。代表性体积元的网格划分如图2所示。

为了测出代表性体积元的力学性能，预测整个复合材料的力学性能，在有限元模型上施加了三个约束和一个位移载荷，三个约束分别加在XOY面，XOZ面和YOZ面，XOY面上的约束限制Z轴方向上的自由度，同理XOZ面和YOZ面分别限制Y轴和X轴方向上的自由度。位移载荷加在XOZ面的对面上，方向沿Y轴正方向，位移载荷的大小随着时间的增加而逐渐变大，其大小随时间的变化如表2所示，有限元模型的约束和加载如图3所示。

图2 代表性体积元网格划分模型Fig.2 Mesh of representative volume element

表2 位移载荷随时间的变化 Table 2 Change of displacement load with time

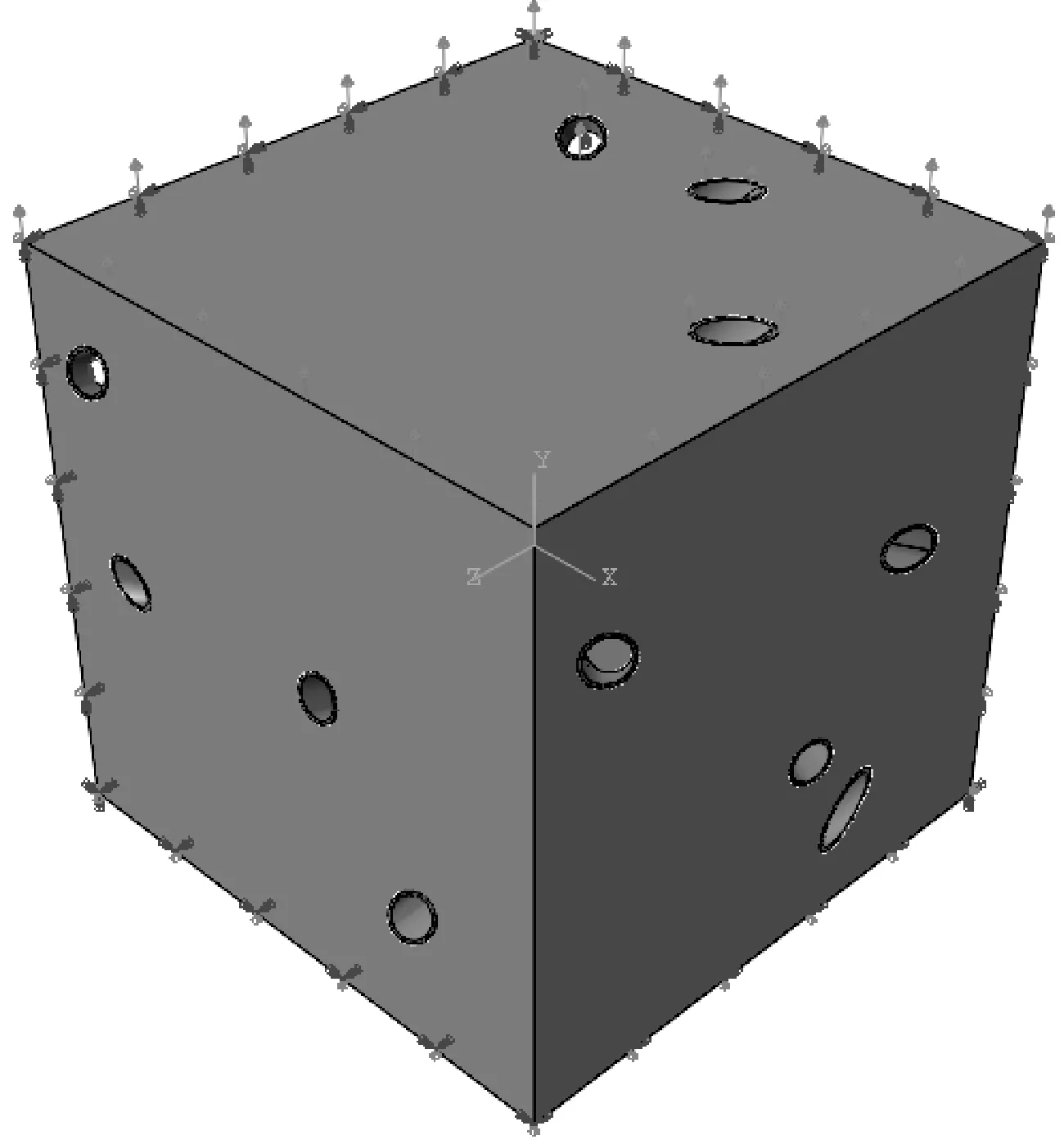
图3 对模型施加载荷和约束Fig.3 Loads and constraints on the model

3.1碳纳米管体积分数对铝基体力学性能的影响

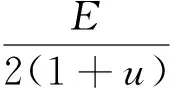
根据屈服强度的定义，金属材料发生屈服现象时的屈服极限通常以产生0.2%残余变形的应力值为其屈服极限，不同体积分数碳纳米管增强的铝基复合材料的屈服强度如图6所示。根据RVE横向应变与纵向应变之比的绝对值得出复合材料的泊松比，泊松比随碳纳米管体积分数的变化如图6所示。

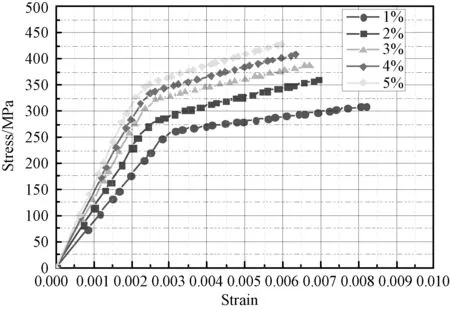
图4 不同体积分数碳纳米管复合材料的应力-应变曲线Fig.4 Stress and strain curves of different volume fractions

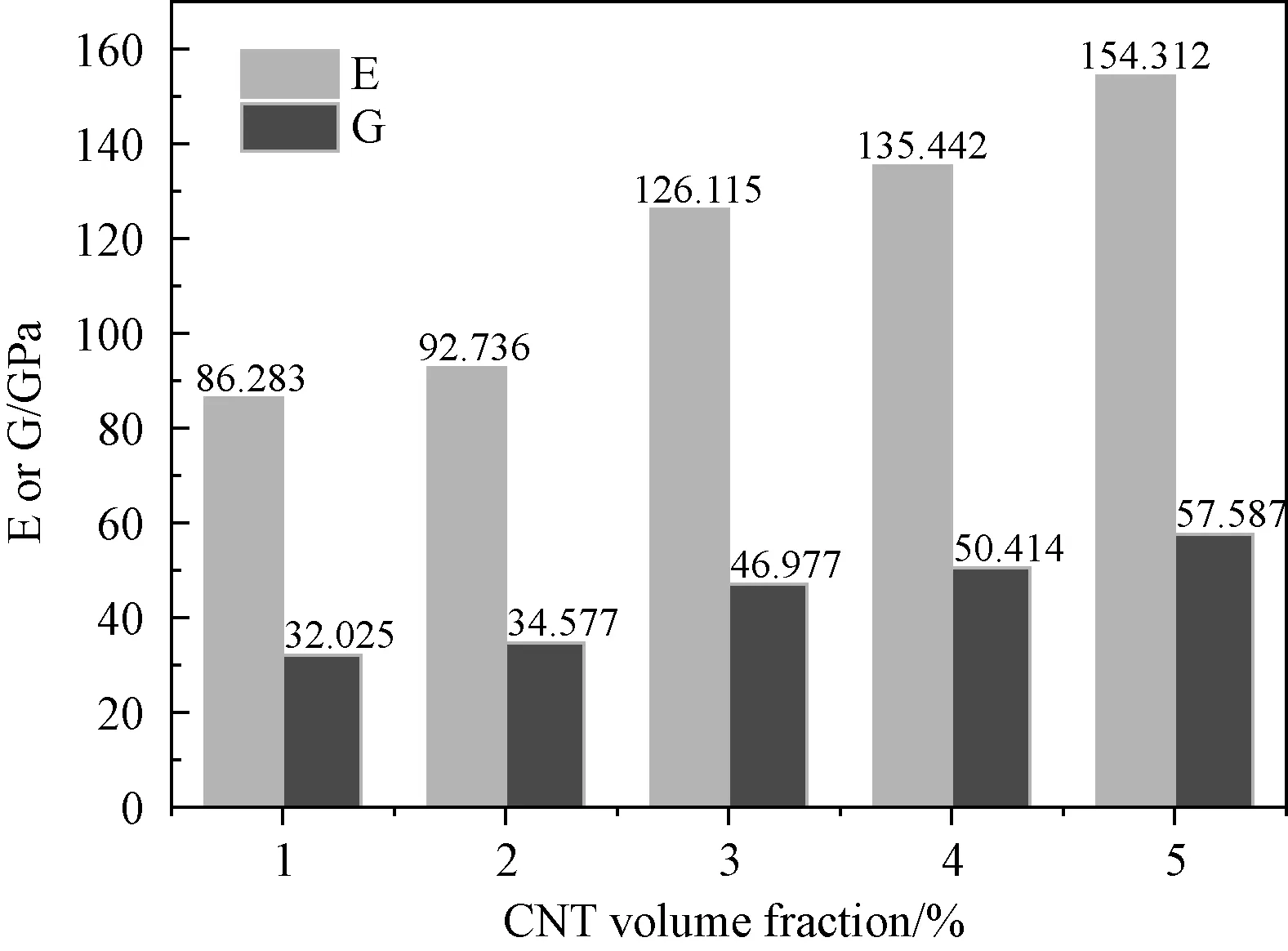
图5 不同体积分数碳纳米管复合材料的弹性模量和剪切模量Fig.5 Different volume fraction of elastic modulus and shear modulus

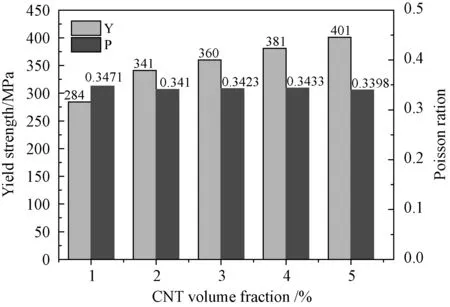
图6 不同体积分数碳纳米管复合材料的屈服强度和泊松比Fig.6 Different volume fraction of the yield strength and poisson ratio

3.2结果与讨论

模拟得到的复合材料和基体力学性能参数及相对变化如表3所示，由表可见，碳纳米管增强的铝基复合材料力学性能得到了显著的改善，当碳纳米管体积分数达到5%时，复合材料的弹性模量、屈服强度和剪切模量分别达到了154GPa、401MPa和57GPa，与铝基体相比分别提高了120%、64%和128%，模拟计算得到的数据与邓春锋等人[20]所做的实验数据基本吻合，实验数据如表4所示。

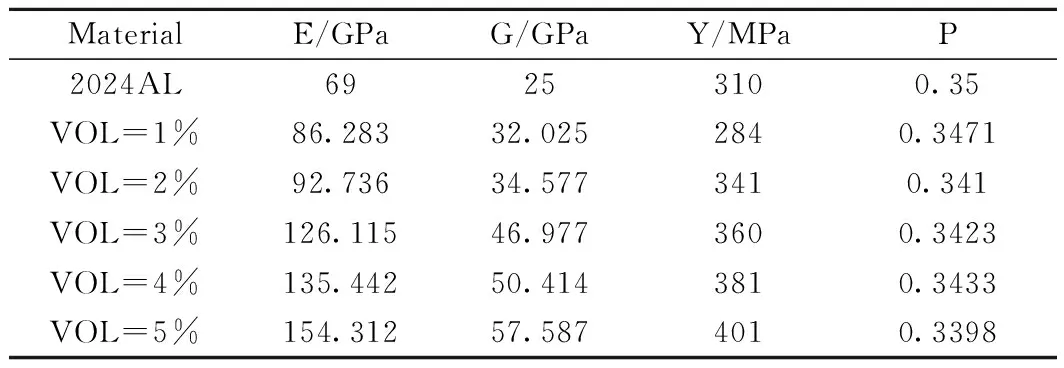
表3 复合材料和基体的力学性能的对比研究

表4 复合材料和基体的力学性能实验数据[20]

因此，随着碳纳米管的加入，复合材料的力学性能都明显提高，说明碳纳米管对铝基体材料起到较好的增强作用。其强化机理可能是碳纳米管优异的力学性能[21-25]，使复合材料在受拉伸时，一方面可以承受较大的应力不易断裂，另一方面碳纳米管在基体内能阻碍裂纹长大与扩展。由于碳纳米管的尺寸较小，可以将碳纳米管等效为细小粒子，这种细小粒子可以起到弥散强化的作用[20]，能抑制基体晶粒的粗化与长大，同时阻碍位错的迁移，提高复合材料的抗变形能力。

4 结 论

采用代表性体积元的方法建立了碳纳米管增强铝基复合材料的模型，运用有限元分析软件ABAQUS对模型的力学性能进行了模拟分析。

1.随着碳纳米管体积分数的增加，碳纳米管增强铝基复合材料的弹性模量、剪切模量和屈服强度都明显增加，但泊松比略有减小。

2.碳纳米管能够明显改善铝基体的力学性能。

[1] 谢桂兰,吴涛,赵锦枭,曹尉南.原位生长碳纳米管增强复合材料风机叶片性能测试[J].材料科学与工程学报, 2014, 32(1):89～92.

[2] Singhal S K, Pasricha R, Jangra M, et al. Carbon Nanotubes: Amino Functionalization and Its Application in the Fabrication of Al-matrix Composites[J]. Powder Technology, 2011, 215/16(1): 254～263.

[3] Bradbury C R, Gomon J K, Kollo L, et al. Hardness of Multi Wall Carbon Nanotubes Reinforced Aluminium Matrix Composites[J]. Journal of Alloys & Compounds, 2014, 585(3):362～367.

[4] 李景瑞,蒋小松,等.碳纳米管增强铝基复合材料的界面特性及增强机理研究进展[J]. 材料导报A(综述篇), 2015, 29(1):31～36.

[5] Kuzumaki T. Processing of Carbon Nanotube Reinforced Aluminum Composite[J]. Journal of Materials Research, 1998, 13(9):2445～2449.

[6] Bakshi S R, Lahiri D, Agarwal A. Carbon Nanotube Reinforced Metal Matrix Composites-a Review[J]. International Materials Reviews, 2010, 55(1):41～64.

[7] 易健宏,鲍瑞. 粉末冶金在CNTs增强金属基复合材料中的应用[J]. 粉末冶金工业, 2015, 25(1):1～7.

[8] 董占青,王筱峻, 等.粉末冶金法制备碳纳米管增强金属基复合材料研究进展[J]. 材料导报A:综述篇, 2014, 28(11):36～41.

[9] Esawi A M K, Morsi K, Sayed A, et al. Fabrication and Properties of Dispersed Carbon Nanotube-aluminum Composites[J]. Materials Science & Engineering A, 2009, 508(1):167～173.

[10] 张晓宇,黄再兴. 连续介质理论在研究碳纳米管力学性能中的应用进展[J].机械强度, 2005, 25(3):324～330.

[11] Tian W, Qi L, Zhou J, et al. Representative Volume Element for Composites Reinforced by Spatially Randomly Distributed Discontinuous Fibers and Its Applications[J]. Composite Structures, 2015, 131:366～373.

[12] 李维学,张胡军,戴剑锋,等.碳纳米管增强镁基复合材料热残余应力的有限元分析[J]. 复合材料学报, 2011, 28(1):166～171.

[13] 章继峰,王振清,周健生,张博明.基于Python_Abaqus复合材料代表性体积元的数值模型[J].宇航材料工艺, 2009, 39(3):25～29.

[14] Chanteli A, Tserpes K I. Finite Element Modeling of Carbon Nanotube Agglomerates in Polymers[C]. Iccs, 2015, 1141～1148.

[15] 黄光杰,汪凌云. 热处理对2024铝合金组织和性能的影响[J].重庆大学学报(自然科学版), 2000, 23(4):99～102.

[16] 辜萍,王宇,李广海.碳纳米管的力学性能及碳纳米管复合材料研究[J]. 力学进展, 2002, 32(4):563～578.

[17] Pan Z W, Xie S S, Chang B H, et al. Very Long Carbon Nanotubes[J]. Nature, 1998, 394(6694):631～632.

[18] 张振华,彭景翠,陈小华.碳纳米管弹性模量的研究[J]. 稀有金属材料与工程, 2004, 33(12):1233～1237.

[19] Shintani K, Narita T. Atomistic Study of Strain Dependence of Poisson’s Ratio of Single-walled Carbon Nanotubes[J]. Surface Science, 2003, 535(03):862～868.

[20] 邓春锋,马艳霞, 等. 碳纳米管增强2024铝基复合材料的力学性能及断裂特性[J].材料科学与工艺, 2010, 18(2):229～232.

[21] 丁志鹏,张孝彬, 等.碳纳米管/铝基复合材料的制备及摩擦性能研究[J].浙江大学学报(工学版), 2005, 39(11):1811～1815.

[22] Wong E W, Sheehan P E, Lieber C M. Nanobeam Mechanics: Elasticity, Strength, and Toughness of Nanorods and Nanotubes[J]. Science, 1997, 277(5334):1971～1975.

[23] Falvo, M. R, Clary, et al. Bending and Buckling of Carbon Nanotubes Under Large Strain. (cover story)[J]. Nature, 1997, 389(6651): 582～584.

[24] Treacy M M J, Ebbesen T W, Gibson J M. Exceptionally High Young’s Modulus Observed for Individual Carbon Nanotubes[J]. Nature, 1996, 381(6584):678～680.

[25] 沈利华,张孝彬, 等. Co/MgO 固体催化剂CVD法合成单壁纳米碳管的研究[J]. 浙江大学学报:工学版, 2003, 37(6): 729～733.

NumericalSimulationofMechanicalPropertiesofCarbonNanotubesReinforcedAluminumMatrixComposites

ZHAOLeilei1,DENGYongsheng1,ZHOULi2,LIDezhi1

(1.NortheasternUniversity,CollegeofMechanicalEngineering,Shenyang110000,China;2.Shenyanguniversityoftechnology,CollegeofMechanicalEngineering,Shenyang110000,China)

In this paper, according to the theory of continuous medium, the method of representative volume element was adopted to calculate the mechanical properties of carbon nanotubes reinforced aluminum matrix composites. The ABAQUS of finite element software was used to analyze the representative volume element model in order to obtain the effects of the different volume fraction of carbon nanotubes on the mechanical properties of the composites. The properties included the elastic modulus, yield strength, poisson ratio and shear modulus. The analysis results show that the volume fraction of carbon nanotubes has a significant influence on the mechanical properties of the composites. With the increase of the volume fraction of the carbon nanotubes, the elastic modulus, yield strength and shear modulus of the composites have obviously improved. The poisson ration decrease slightly.

Carbon nanotubes Aluminum Matrix Composites; representative volume element; mechanical property; finite element

TB331

：ADOI:10.14136/j.cnki.issn1673-2812.2017.04.030

2016-04-21；

：2016-05-30

教育部中央高校基本科研业务资助项目(N140304011)

赵磊磊(1992-)，硕士研究生，研究方向：复合材料。E-mail：leileizhao233@163.com。

周 丽(1971-)，教授，研究方向：复合材料。E-mail：lizhou@imr.ac.cn。

1673-2812(2017)04-0667-05