磁场作用下磁流变液剪切性能的实验分析

，， ，

(山东科技大学 机械电子工程学院，山东 青岛 266590)

磁场作用下磁流变液剪切性能的实验分析

肖林京，王传萍，卫洁，朱绪力

(山东科技大学机械电子工程学院，山东青岛266590)

本文研究了磁流变液的力学性能，制备了羰基铁粉体积分数为20%的硅油基磁流变液，观察了磁流变液在磁场作用下的微观变化，测试了磁流变液的剪切性能。实验表明，无磁场作用下，磁流变液为牛顿流体；在磁场作用下，随着剪切速率的增加，剪切应力趋于稳定，表观粘度呈现指数式下降，磁流变液具有剪切稀化效应，符合广义Bingham模型。磁流变液剪切应力和外加电流的依赖关系为：在电流较小时，剪切应力表现为指数增长，指数值约为1.5；随着外加电流的增大，剪切应力表现为线性增长，最终达到稳定值。

磁流变液； 力学性能； 磁场； 本构模型

1 前 言

磁流变液是微米尺寸的磁极化颗粒分散于非磁性液体(矿物油、硅油等)中形成的悬浮液[1]，其基本特征是在不加磁场时表现牛顿流体特性；在外加磁场时，其微观结构和宏观力学行为会发生显著变化，表现出“类固体”特性，具有一定的抗剪屈服应力。磁流变液具有可控、快速、可逆的优点[2]，使其在振动控制、传动控制、液压控制、抛光、柔性夹具等机械领域显示出了强大的应用潜力[3]。

磁流变材料的制备、流变机理、力学行为一直是该领域的研究热点和重点[4-6]，Bossis等[2]对磁流变液的屈服应力进行了研究，发现屈服应力和磁场之间存在依赖关系；魏齐龙等[5]研究了磁场作用下磁流变液的流变行为；王鸿云等[6]研究了磁场作用下磁流变液的挤压与拉伸特性；易成建[7]对磁流变液的性能进行了测试，并观察了磁流变液的微观变化；Imaduddin等[8]对磁流变液在阻尼器中的应用进行了分析。但目前对磁流变液剪切应力的分析，仅局限于宏观现象，没有将宏观性能变化和磁性颗粒运动的微观机理结合起来。本文通过实验方法，对磁场作用下磁流变液剪切应力和表观粘度的变化进行了测量，分析了磁流变液宏观性能变化的微观运动机理。通过对数拟合方法，研究在不同电流下，磁流变液剪切应力和外加电流的对应关系，对深入研究磁流变液力学性能提供了实验依据。

2 本构模型

基本Bingham模型可表示为：

(1)

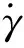
基本 Bingham模型虽然简洁易用，但无法对磁流变液的应力应变过程进行完整的描述，尤其是磁流变液的剪切稀化现象。针对基本Bingham模型的局限性，翁建生等[8]提出了基于Bingham模型的广义Bingham模型。广义Bingham模型可以表示为：

(2)

其粘度与剪切速率的关系为：

(3)

式中：K为磁流变液的塑性粘度系数；n为流动特性指数。

从公式(2)和(3)可以看出，当n>1，流体表征为剪切增稠现象；n<1，流体表征为剪切变稀现象；n=1时，广义Bingham模型就变成了基本Bingham模型。

磁流变液的剪切应力与磁场强度的关系，在剪切应力的计算中，引用最多的是Ginder提出的剪切应力公式[8-10]，它可表示为：

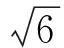
(4)

式中，φ为磁性颗粒的体积分数；μ0为真空磁导率；Ms为磁性颗粒的饱和磁化强度；H为磁场强度。

在本文中，磁性颗粒的体积分数、饱和磁化强度和真空磁导率均为常数，由公式(4)可得出：磁流变液的剪切应力仅与磁场强度相关。

3 实 验

3.1磁流变液样品制备

选用羰基铁粉作为磁性颗粒，二甲基硅油作为基液，硬脂酸作为表面活性剂，制备羰基铁粉体积分数为20%的磁流变液，硬脂酸的质量分数为羰基铁粉的2%，按计算的配比称取羰基铁粉、硬脂酸和二甲基硅油。羰基铁粉的平均粒径为3.3μm，二甲基硅油的粘度为10cst。

磁流变液的制备流程分为3步：(1)磁流变液和硬脂酸混合，放入球磨机进行研磨10h；(2)将二甲基硅油倒入混合物中，继续研磨10h；(3)将混合物取出，放入真空干燥箱进行抽真空。制备的磁流变液样品如图1所示。

图1 磁流变液的样品照片Fig.1 Samples of MRFs

3.2磁流变液的微观观察

实验采用Keyence的VHX-600超景深三维数码显微镜对磁流变液在磁场作用下的微观变化进行观察。

将制备好的磁流变液滴一滴在载玻片上，盖上盖玻片，使液滴铺展均匀。通过永磁铁对磁流变液施加磁场，永磁铁的磁感应强度分别为15mT、75mT和150mT。磁流变液的微观变化如图2所示。

由图2可以看出，当外加磁场较小时，磁流变液中的通链数较少且链长较短，颗粒链多以孤立链和支链的形式存在，随着外加磁场的增大，颗粒链相互聚集形成链柱结构，链的平均长度增加，孤立链的数量减少，通链增多。

3.3磁流变液的剪切测试

实验采用Anton Paar Physica MCR 301平板测试流变仪对磁流变液的剪切性能进行测试。测试时，将磁流变液放入流变仪上、下平板之间，在无磁场的条件下以50s-1的剪切速率剪切150s，以保证磁流变液良好的分散性。然后在不同条件下测量磁流变液的剪切应力。

设置外加电流为0，剪切速率为0～100s-1，温度为25℃，剪切时间为10s，每0.1s取样一次，其他参数采用默认值，测量磁流变液剪切应力的变化。

图2 磁感应强度分别为(a)0，(b)15mT，(c)75mT，(d)150mT时的磁流变液的微观形态变化图Fig.2 Micro-morphological changes of MRFs when magnetic flux density is (a) 0, (b) 15mT, (c) 75mT, (d) 150mT

设置外加电流为1A，剪切速率为100～1000s-1，温度为25℃，剪切时间为10s，每0.1s取样一次，其他参数采用默认值，测量磁流变液剪切应力和表观粘度的变化，然后将外加电流依次增大为2A、3A、4A，其他参数保持不变，依次测量磁流变液剪切应力和表观粘度的变化。

设置剪切速率为300s-1，电流在0.1～4A范围内变化，温度为25℃，剪切时间为10s，每0.1s取样一次，其他参数采用默认值，测量磁流变液剪切应力的变化。

4 实验结果及分析

无磁场时磁流变液剪切应力的拟合结果如图3所示。从图3可以看出：随着剪切速率的增加，剪切应力增大，其范围为0.2～2Pa。从拟合结果可以看出，磁流变液的剪切应力和剪切速率呈线性关系。由此可以得出，无磁场时，磁流变液为牛顿流体。

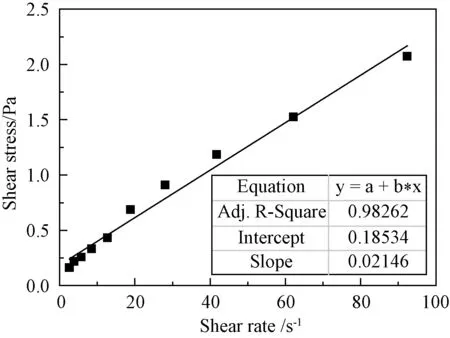
图3 无磁场时剪切应力的拟合曲线图Fig.3 Fitting results of shear stress without magnetic field

磁场作用下，磁流变液剪切应力的变化如图4所示。从图4(a)看出，剪切应力随剪切速率的增加变化并不明显。相同剪切速率下，剪切应力随外加电流的增大而显著增大，范围为8～31kPa。磁流变液表观粘度的拟合结果如图4(b)所示。从图4(b)看出，在双对数坐标下，表观粘度和剪切速率呈线性关系。因此可见表观粘度和剪切速率之间存在指数关系，随着剪切速率的增大，表观粘度呈现指数式下降，范围为10～245Pa·s。

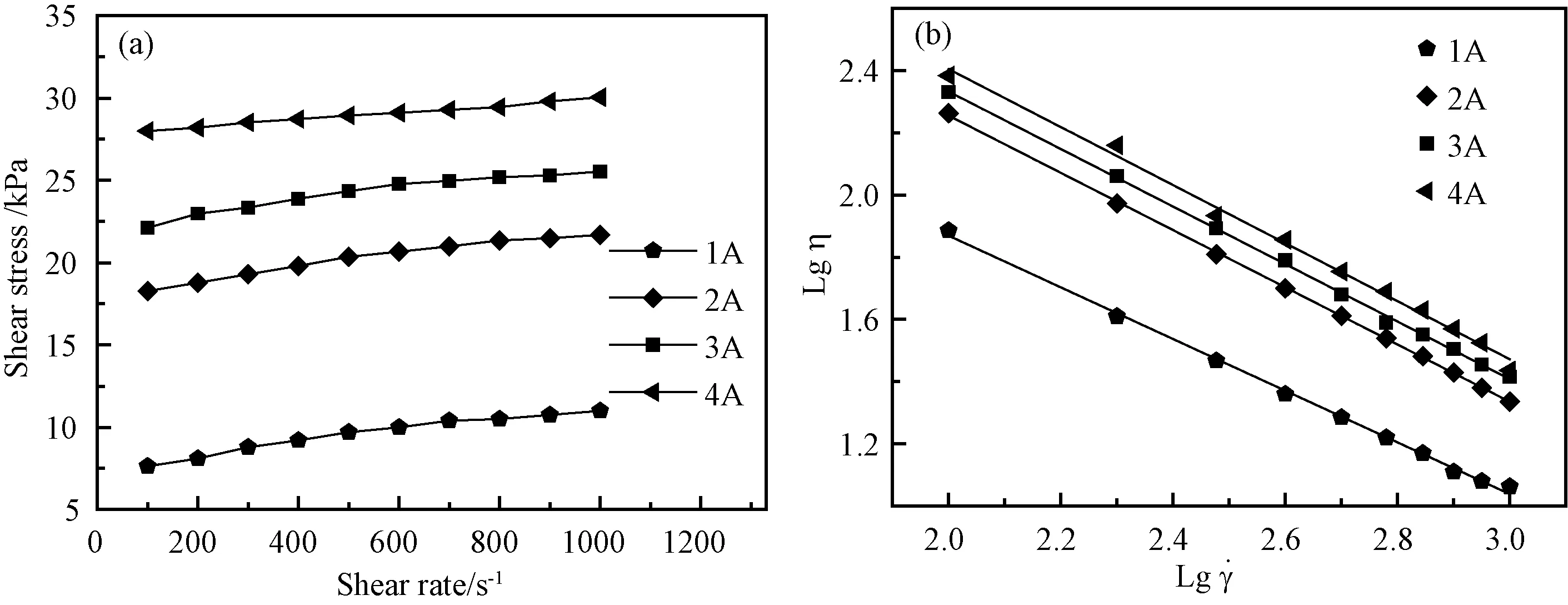
图4 磁流变液的剪切性能 (a) 不同电流下剪切应力变化； (b) 不同电流下表观粘度的拟合Fig.4 Shear behavior of magnetorheological fluids(a) Dependence of shear stress on different current; (b) Fitting of apparent viscosity at different current

运用公式(3)对表观粘度和剪切速率关系进行对数拟合，拟合计算结果如表1所示。由表1可以看出，随着外加电流的增大，磁流变液的塑性粘度系数K增大，流动特性指数n减小。由此可以得出，外加电流越大，磁流变液粘度越大，流动性越小，磁流变液具有剪切稀化效应，符合广义Bingham模型，并且外加电流越大，磁流变液剪切稀化效应越明显。

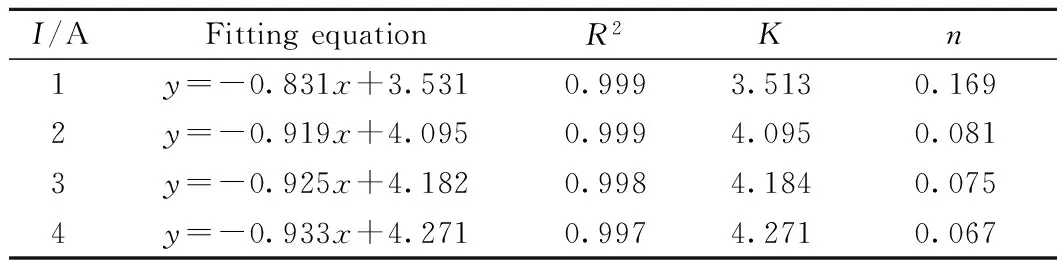
表1 表观粘度的拟合结果

在磁场作用下，磁流变液中的铁磁性颗粒排列成链状结构，当磁流变液开始剪切时，平板之间的颗粒链被拉长后断裂，磁场作用下新的颗粒链形成。随着剪切速率的增加，颗粒链的断裂和形成会达到平衡，剪切应力达到一稳定值。外加电流越大，磁流变液中颗粒链之间相互作用力越强，宏观表现为剪切应力越大。由此可以得出，剪切速率增加时，剪切应力趋于稳定值，剪切应力变化趋势符合广义Bingham模型，存在剪切稀化现象。

磁流变液的剪切应力和外加电流的关系如图5所示。从图5可以看出，随着外加电流的增大，剪切应力显著增大，范围为500Pa～27kPa。磁流变液的剪切应力和外加电流的拟合结果如图6所示，由图6(a)可以看出：剪切应力和电流在双对数坐标下为线性关系。由此可以得出，外加电流在0～1A范围内，磁流变液的剪切应力和外加电流之间存在指数关系，指数值约为1.5。从图6(b)可以看出：剪切应力和电流在普通坐标下为线性关系。由此可以得出，外加电流在1～2A范围内，磁流变液的剪切应力和外加电流之间存在线性关系。

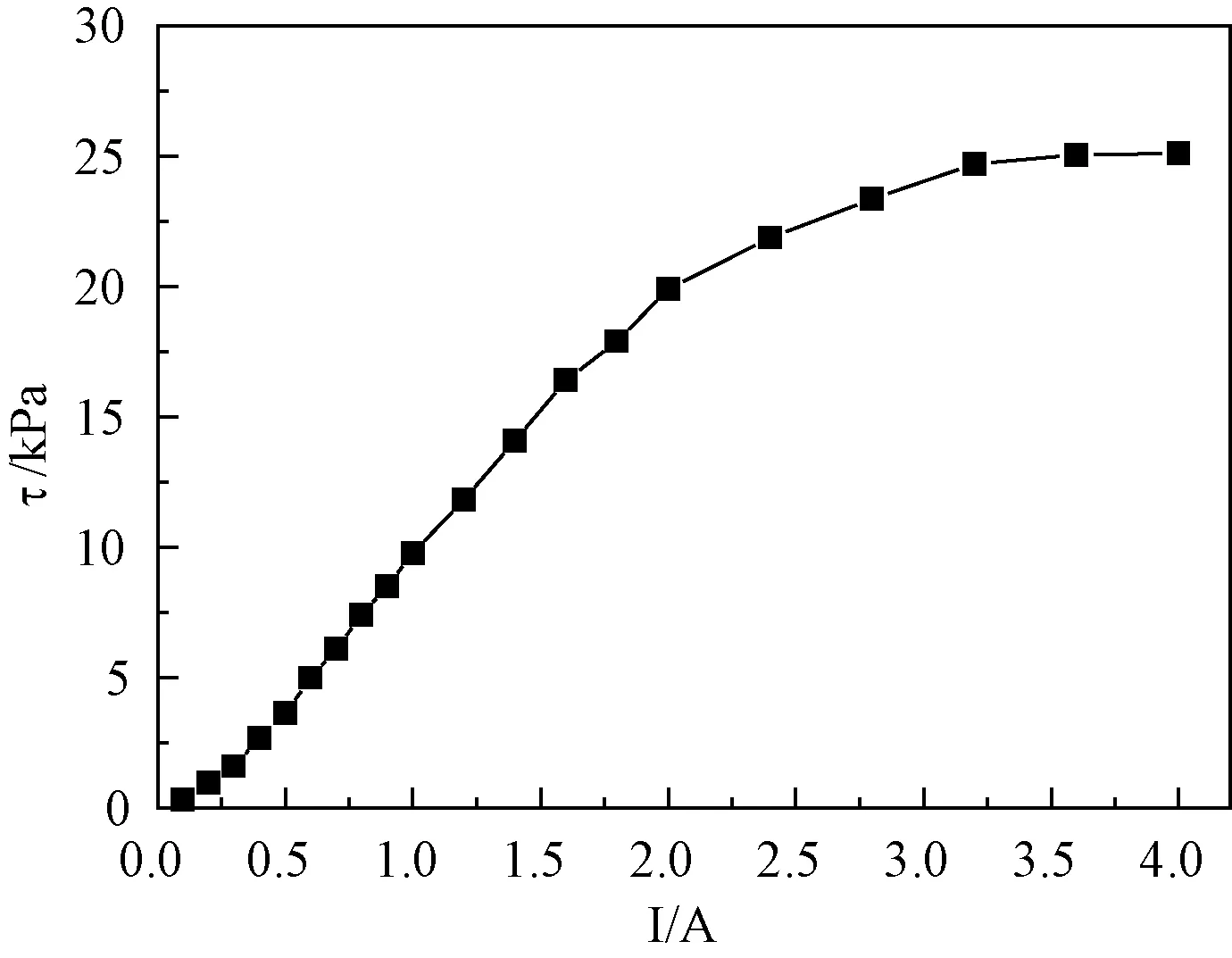
图5 剪切应力和外加电流之间的关系Fig.5 Dependence of shear stress on external current

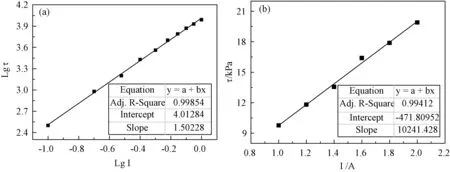
图6 磁流变液的剪切应力和外加电流的拟合曲线 (a) 0～1A； (b) 1～2AFig.6 Fitting curve of shear stress and applied current of magnetorheological fluid (a) 0～1A; (b) 1～2A

磁流变液剪切应力和外加电流的关系可以用颗粒间磁场力来解释[11]。当磁场较小时，磁流变液内的铁磁性颗粒远未达到磁化饱和，在磁场作用下，颗粒相互作用，形成链柱结构，磁流变液的宏观剪切应力增加较快，呈现指数式增长。随着磁场的增大，磁流变液内的铁磁性颗粒局部磁化饱和，磁流变液的宏观剪切应力增加平稳，呈现线性增长。随着磁场继续增大，颗粒接近完全磁化饱和时，磁流变液的宏观剪切应力变化很小，颗粒完全磁化饱和后，磁流变液的宏观剪切应力达到稳定值。由此可以得出，磁流变液剪切应力和外加电流的依赖关系为：在电流较小时，剪切应力表现为指数增长，指数值约为1.5；随着外加电流的增大，剪切应力表现为线性增长，最终达到稳定值。

5 结 论

无磁场时，磁流变液为牛顿流体。在磁场作用下，随着剪切速率的增加，磁流变液剪切应力变化并不明显，而表观粘度呈现指数式下降。相同剪切速率下，随着外加电流的增大，磁流变液剪切应力和表观粘度增大。磁流变液具有剪切稀化效应，符合广义Bingham模型，并且外加电流越大，磁流变液剪切稀化效应越明显。

磁流变液剪切应力和外加电流的依赖关系为:在电流较小时，剪切应力表现为指数增长，指数值约为1.5；随着外加电流的增大，剪切应力表现为线性增长，最终达到稳定值。

[1] H.See. Field dependence of the response of a magnetorheological suspension under steady shear flow and squeezing flow [J]. Rheologica Acta, 2003, 42(1/2):86～92.

[2] G.Bossis, P.Khuzir, S.Lacis, O.Volkova. Yield behavior of magnetorheological suspensions [J]. Journal o f Magnetism and Magnetic Materials, 2003, 258/259(258): 456～458.

[3] 黄炼,查长松. 磁流变弹性体的磁致性能[J]. 材料科学与工程学报, 2016, 34(1):139～141.

[4] 王宇飞,何琳,杨雪,帅长庚. 磁流变弹性体的研究现状及工程应用[J]. 材料科学与工程学报, 2010, 28(4):633～636+632.

[5] 魏齐龙,王超,罗清,何建国.磁场作用下磁流变液的流变行为[J].磁性材料及器件, 2013, 44(1):6～9+43.

[6] 王鸿云,高春甫,阚君武,李泳鲜,王笑.磁场作用下磁流变液的挤压与拉伸特性[J].光学精密工程, 2011, 19(4):850～856.

[7] 易成建,彭向和,孙虎. 基于有限元方法的磁流变液微结构磁化及宏观力学特性分析[J]. 功能材料, 2011, 42(8):1500～1503.

[8] F.Imaduddin, S.Mazlan, H.Zamzuri. A design and modelling review of rotary magnetorheological damper [J]. Materials and Design, 2013, 51(5):575～595.

[9] 翁建生,胡海岩,张庙康.磁流变液体的流变力学特性试验和建模[J].应用力学学报, 2000, 17 (3):1～5+140.

[10] S.M.Fayyad. Experimental investigation of using MR! fluids in automobiles suspension systems[J]. Research Journal of Applied Sciences Engineering and Technology, 2010, 2(2):159～164.

[11] 朱绪力,孟永钢,田煜.磁流变弹性体中颗粒磁场力的简化分析模型[J].功能材料, 2010, 41(10): 1712～1715.

ExperimentalAnalysisonShearPropertiesofMagnetorheologicalFluidsunderMagneticFields

XIAOLinjing,WANGChuanping,WEIJie,ZHUXuli

(CollegeofMechanicalandElectronicEngineering,ShandongUniversityofScienceandTechnology,Qingdao266590,China)

Mechanical properties of magnetorheological fluids (MRFs) were studied. Silicone-based MRFs were prepared with 20% volume fraction of carbonyl iron powder. The Keyence VHX-600 super depth 3D digital microscope was used to observe the microscopic movement of MRFs under magnetic fields. Rheometer Physica MCR 301 was used to test shear properties of MRFs. The experimental results show that MRFs are Newtonian fluids without magnetic field. Shear stress of MRFs remains stable but apparent viscosity decreases exponentially with the increase of shear rate under magnetic fields. MRFs are shear thinning of Bingham fluids in the presence of magnetic field and conform to the generalized Bingham model. Shear stress increases also exponentially with the index value is about 1.5 when the external current is low. With the increase of external current, shear stress increases at a linear trend and eventually reaches a stable value.

magnetorheological fluid; mechanical property; magnetic field; constitutive model

TM271

：ADOI:10.14136/j.cnki.issn1673-2812.2017.04.028

1673-2812(2017)04-0659-05

2016-02-26；

：2016-04-19

山东省自然科学基金资助项目(ZR2011EEM005)，山东科技大学研究生科技创新基金资助项目(SDKDYC170326)

肖林京(1966-)，男，教授，博士，研究方向：机电传动控制。E-mail:1527510435@qq.com。

王传萍(1991-)，女，硕士，研究方向：磁流变减振器设计。E-mail:wangchuanping10@163.com。