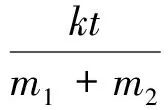判断叠放体是否做相对运动的两种方法
陆群丰(浙江省慈溪市杨贤江中学 浙江 宁波 315300)

判断叠放体是否做相对运动的两种方法
陆群丰
(浙江省慈溪市杨贤江中学 浙江 宁波 315300)
对叠放在水平面上的两个物体在水平方向拉力作用下是否做相对运动问题进行了探讨,提出了临界拉力、临界加速度的概念,导出判断是否相对运动的条件.
相对运动 静摩擦力 临界拉力 临界加速度
叠放在水平面上的物体,在拉力F的作用下,两物体可能一起以相等的加速度运动,也可能分别以不同的加速度运动,两物体之间有相对运动.本文通过引导和讨论,介绍两种判断叠放体是否做相对运动的方法.
1 当拉力作用在叠放体的上层物体上时
1.1当两物体一起以相同的加速度运动时拉力的取值范围
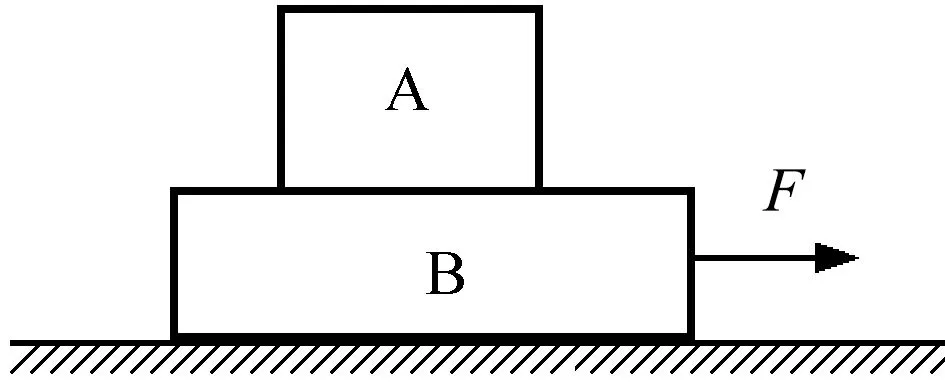
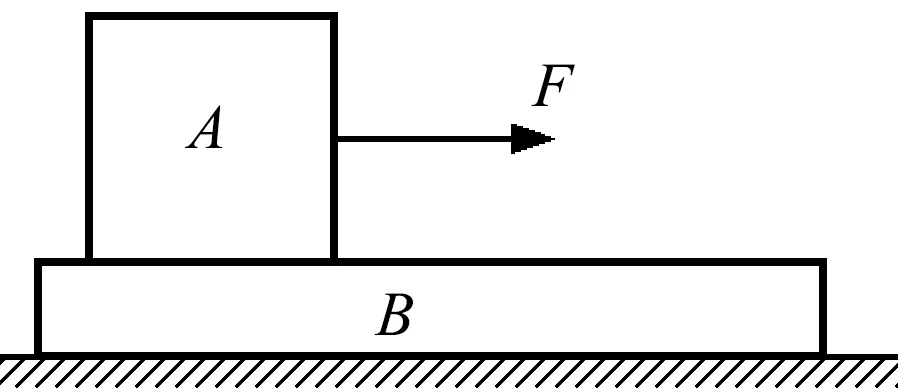
如图1所示,在粗糙的水平面上叠放着两个质量分别为m1和m2的物体A和B,两物体之间以及B与地面之间的动摩擦因数分别为μ1和μ2,现给上层物体A施加拉力F,使两物体一起以相同的加速度运动,根据牛顿第二定律,对整体有
F-μ2(m1+m2)g=(m1+m2)a
(1)
对A
F-Ff=m1a
(2)
对B
Ff-μ2(m1+m2)g=m2a
(3)
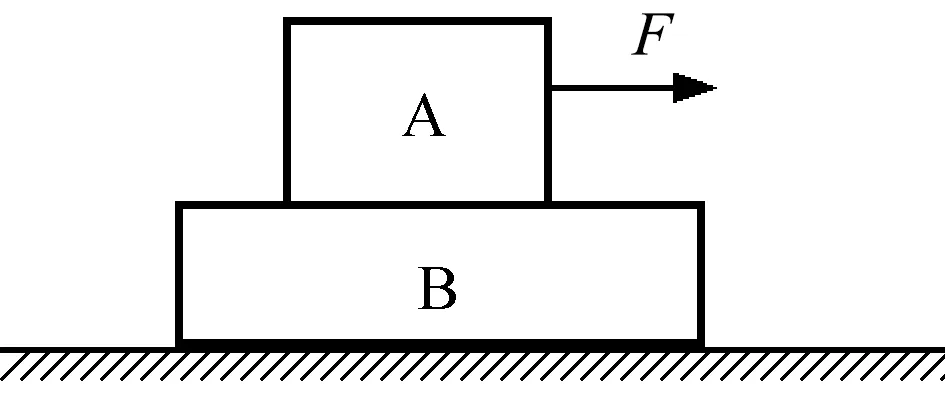
图1 作用力施加于上层物体
当两物体一起运动时,物体之间的摩擦力Ff是静摩擦力,应小于最大静摩擦力,若把最大静摩擦力按滑动摩擦力计算,则两物体刚要发生相对运动时,有
F-μ1m1g=m1a0
(4)
其中a0是临界加速度.对比式(2)可知加速度a>a0.
当两物体一起运动时,考虑下层物体B的受力,一定有物体之间的最大静摩擦力大于物体B与地面之间的最大静摩擦力,即
μ1m1g>μ2(m1+m2)g
这是物体B能够运动的力学前提.
可见,物体之间的静摩擦力Ff应在范围
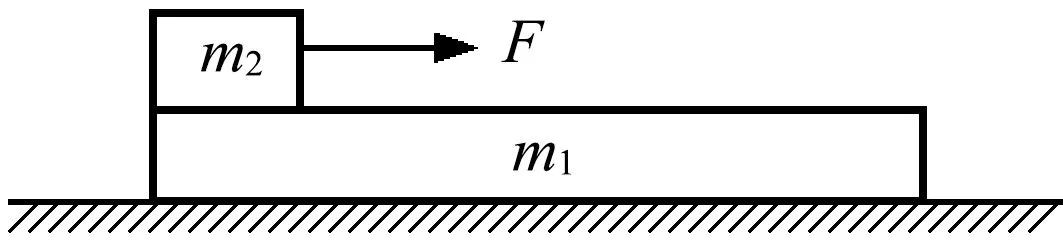
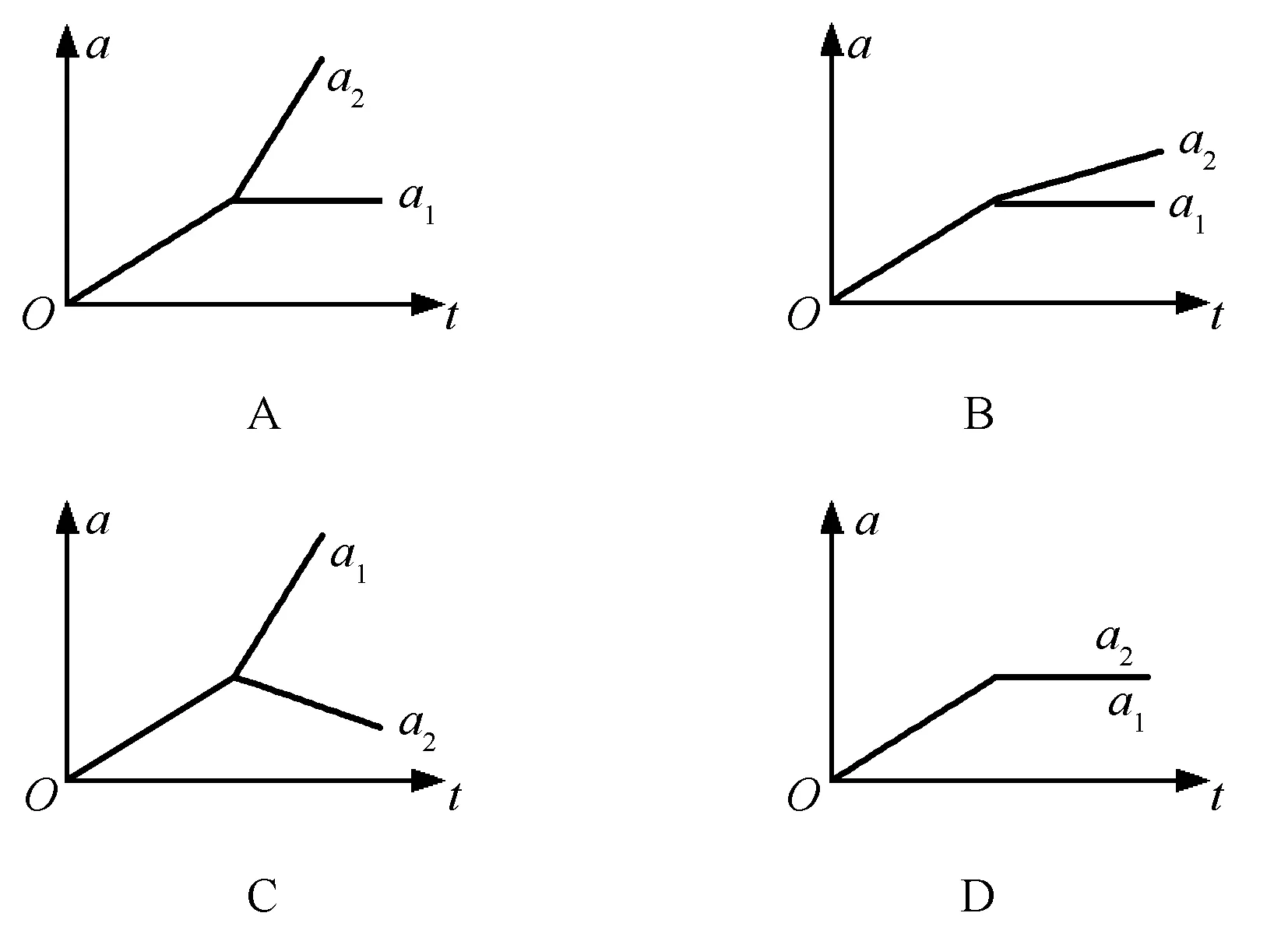
μ2(m1+m2)g 以内. 由式(2)、(3)得 再结合静摩擦力Ff的取值范围,可知当两物体一起运动时,拉力F的取值范围是 (5) 小结1:若拉力作用在叠放体的上层物体上,可得如下结论. (1)当拉力满足式(5)时,两物体一起以相同的加速度运动. (2)当两物体一起运动的加速度大于物体之间的临界加速度(即a>a0)时,两物体一起以相同的加速度运动.计算加速度的方法是式(1),计算临界加速度的方法是式(4). 1.2当两物体以不同的加速度运动时拉力的取值范围 如果在拉力F的作用下,两物体分别以不同的加速度运动,即两物体之间有相对运动时,根据牛顿第二定律,对整体有 F-μ2(m1+m2)g=m1a1+m2a2 (6) 对A F-μ1m1g=m1a1 (7) 对B μ1m1g-μ2(m1+m2)g=m2a2 (8) 根据以上讨论,当 (9) 两物体以不同的加速度运动. 根据实际物理情景,应有两物体A和B的加速度a1>a2. “假设两物体一起以相等的加速度a运动”(强调:这种情况是为了做比较而假设出来的,把这个加速度姑且称为虚拟加速度),则满足式(1). 对比式(6)和式(1)等号右边,有 m1a1+m2a2=(m1+m2)a 可得 a1>a>a2 其中a1就是这种情况下的临界加速度. 小结2:若拉力作用在叠放体的上层物体上,可得如下结论. (1)当拉力满足式(9)时,两物体以不同的加速度运动. (2)当两物体一起运动的虚拟加速度小于物体之间的临界加速度(即a1>a)时,两物体以不同的加速度做相对运动,且上层物体的加速度、虚拟加速度和下层物体的加速度满足关系a1>a>a2.计算虚拟加速度的方法是式(1),计算临界加速度的方法是式(7). 总结1:当拉力作用在叠放体的上层物体上时,可得如下结论. (1)根据拉力判断,若拉力小于临界拉力 则两物体以相同的加速度一起运动.若拉力大于临界拉力F0,则两物体以不同的加速度做相对运动. (2)根据加速度判断,若由式(1)计算得到的加速度大于由F-μ1m1g=m1a计算得到的加速度,则两物体以相同的加速度一起运动.若由式(1)计算得到的加速度小于由式(7)计算得到的加速度,则两物体以不同的加速度做相对运动,且上层物体的加速度、虚拟加速度和下层物体的加速度满足关系a1>a>a2. 图2 例1题图 A.当F<2μmg时,A和B都相对地面静止 C.当F>3μmg时,A相对B运动 解析:根据以上总结1,临界拉力 选项B正确.B具有最大加速度时,由式(8)解得 点评:本题是2014年江苏高考题,试题难度很大,据统计得分率最低,可是如果我们掌握以上结论,便能迎刃而解. 2.1当两物体一起以相同的加速度运动时拉力的取值范围 如图3所示,在粗糙的水平面上叠放着两个质量分别为m1和m2的物体A和B,两物体之间以及B与地面之间的动摩擦因数分别为μ1和μ2,现给B施加拉力F,使两物体一起以相同的加速度运动,根据牛顿第二定律,对整体仍满足式(1),对A Ff=m1a (10) 对B F-Ff-μ2(m1+m2)g=m2a (11) 图3 作用力施加于下层物体 当两物体一起运动时,物体之间的摩擦力Ff是静摩擦力,应小于最大静摩擦力,若把最大静摩擦力按照滑动摩擦力计算,则两物体刚要发生相对运动时,有 μ1m1g=m1a0 (12) 对比式(10)可知,物体一起运动的加速度小于临界加速度a0,即a 当两物体一起运动时,一定有 F>μ2(m1+m2)g 当两物体一起运动时,物体之间的静摩擦力应在范围Ff<μ1m1g以内. 由式(10)、(11)得 再结合静摩擦力的范围,可知当两物体一起运动时,拉力的取值范围是 F<(μ1+μ2)(m1+m2)g 小结3:若拉力作用在叠放体的下层物体上,可得如下结论. (1)当 μ2(m1+m2)g 时,两物体一起以相同的加速度运动. (2)当两物体一起运动的加速度小于物体之间的临界加速度(a 2.2当两物体以不同的加速度运动时拉力的作用范围 如果拉力F较大,两物体分别以不同的加速度运动,即两物体之间有相对运动,根据牛顿第二定律则,对整体仍满足式(6),对A μ1m1g=m1a1 (13) 对B F-μ1m1g-μ2(m1+m2)g=m2a2 (14) 根据以上讨论,当拉力 F>(μ1+μ2)(m1+m2)g 两物体以不同的加速度运动,即两物体之间有相对运动. 根据实际物理情景,应有两物体B和A的加速度a2>a1. “假设两物体一起以相等的加速度运动” (强调:这种情况是为了做比较而假设出来的,把这个加速度姑且称为虚拟加速度),则有满足式(1). 对比式(6)和式(1)等号右边,有m1a1+m2a2=(m1+m2)a,可得a2>a>a1(其中a1就是这种情况下的临界加速度). 小结4:当拉力作用在叠放体的下层物体上,可得如下结论. (1)当F≥(μ1+μ2)(m1+m2)g时,两物体以不同的加速度运动. (2)当两物体一起运动的虚拟加速度大于物体之间的临界加速度(即a>a1)时,两物体以不同的加速度做相对运动,且下层物体的加速度、虚拟加速度和上层物体的加速度满足关系a2>a>a1.计算虚拟加速度的方法是式(1),计算临界加速度的方法是式(13). 总结2:当拉力作用在叠放体下层物体上时,可得如下结论. (1)根据拉力判断:若拉力小于临界拉力 F0=(μ1+μ2)(m1+m2)g 则两物体以相同的加速度一起运动;若拉力大于临界拉力F0,则两物体以不同的加速度做相对运动. (2)根据加速度判断:若由式(1)计算得到的加速度小于由式(13)计算得到的加速度,则两物体以相同的加速度一起运动. 若由式(1)计算得到的加速度大于由式(13)计算得到的加速度,则两物体以不同的加速度做相对运动,且下层物体的加速度、虚拟加速度和上层物体的加速度满足关系a2>a>a1. 【例2】如图3所示,物体A,B质量分别为m1=1 kg,m2=2 kg,两物体之间以及B与地面之间的动摩擦因数分别为0.3和0.1,求以下两种情况下两物体的加速度: (1)当施加在B上的拉力F为5 N; (2)当施加在B上的拉力F为15 N. 解析:(1)由于满足 F>μ2(m1+m2)g 所以B一定会被拉动. 根据以上知识,拉力F又满足 F<(μ1+μ2)(m1+m2)g 可知两物体一起以相等的加速度运动,物体之间是静摩擦力.由式(1)解得 小于临界加速度3 m/s2. (2)由于拉力 F>(μ1+μ2)(m1+m2)g 因此两物体运动的加速度不同,之间有相对运动,摩擦力是滑动摩擦力.由式(6)、式(13)解得 a1=3 m/s2a2=4.5 m/s2 很显然,这两个物体的加速度a2>a1. “假设两物体一起以相等的加速度运动” (强调:这种情况是为了做比较而假设出来的,因此加速度也是虚拟的),则有满足式(1),解得 a=4 m/s2 这个假设出来的加速度介于两物体的加速度之间. 【精彩习题链接】如图4所示,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是( ) 图4 习题题图 解析:答案是A.在达到最大静摩擦力前,摩擦力为静摩擦力,木块和木板相对静止,以相同加速度运动,根据牛顿第二定律有 随着时间的推移,拉力的线性增大,木块和木板之间发生相对运动,根据总结1,本题加速度应满足“上层物体的加速度、虚拟加速度和下层物体的加速度满足关系a2>a>a1”,所以选项A正确. 2017-01-31)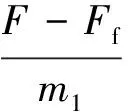
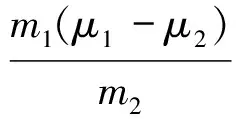
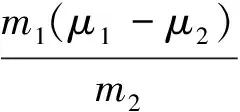

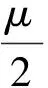
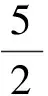
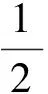

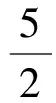
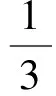
2 当拉力作用在叠放体的下层物体上时