阻尼参数的测量*

姚关心 张彦华 曾宗康(安徽师范大学物理与电子信息学院 安徽 芜湖 241000)

阻尼参数的测量*

姚关心 张彦华 曾宗康
(安徽师范大学物理与电子信息学院 安徽 芜湖 241000)

通过解微分方程和微分等数学手段，给出了滑块通过平衡位置的速度与阻尼因数之间的关系，并利用Origin软件对实验数据进行直线拟合，从而确定振动系统的阻尼因数及其他振动参数.该测量方法容易操作，实验数据易得、可靠且处理简单.

阻尼振动 振动曲线 阻尼因数

振动在自然界中广泛存在，为了研究这方面的问题，我们常常研究物块与弹簧构成的振动系统,以此获得有用的结果.

将两轻质弹簧的一端固定在滑块上，另一端分别固定在气垫导轨的两端，我们在该气轨上可以进行验证简谐振动的周期不变性、研究弹簧质量对振动周期的影响等实验内容[1,2].由于空气阻力的存在，气轨上的滑块是在沿气轨做欠阻尼振动.为了反映空气阻力对滑块振动的影响，我们通常引进半衰期Th，弛豫时间τ,阻尼因数β,粘性阻尼常量γ等振动参数来描述气轨上滑块的阻尼振动.这些振动参数之间满足一定的数学关系，我们可由滑块振动周期T和其他任一振动参数导出其他振动参数.

现行的教材和文献中给出的测量方法[2～6]主要有：(1)半衰期法；(2)弛豫时间法.这些方法中的半衰期测量和振动曲线描绘都存在一定的困难.本文利用严格的数学推导导出欠阻尼振动的速度表达式以及滑块经过无阻尼振动的平衡位置速度与阻尼因数之间的关系，采用直线拟合数据处理方法，得到阻尼振动的阻尼因数β以及其他振动参数,并与拟合Tracker软件获得的振动曲线而得到的阻尼因数β

进行了比较.该测量过程简单易行，数据易得、可靠且处理过程简单，对大学物理实验教学具有一定的借鉴作用.

1 阻尼振动参数的测量原理

1.1阻尼振动的动力学方程

图1所示为气轨上的滑块振动系统，滑块质量为m，其两端分别连接劲度系数为κ1和κ2的轻质弹簧，以系统在无阻尼作用下的平衡位置(后称平衡位置)为x轴坐标原点，水平向右为x轴的正方向，滑块的动力学方程[2]可写为

(1)

式中ω0为振动系统固有频率，β称为阻尼因数

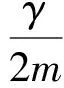
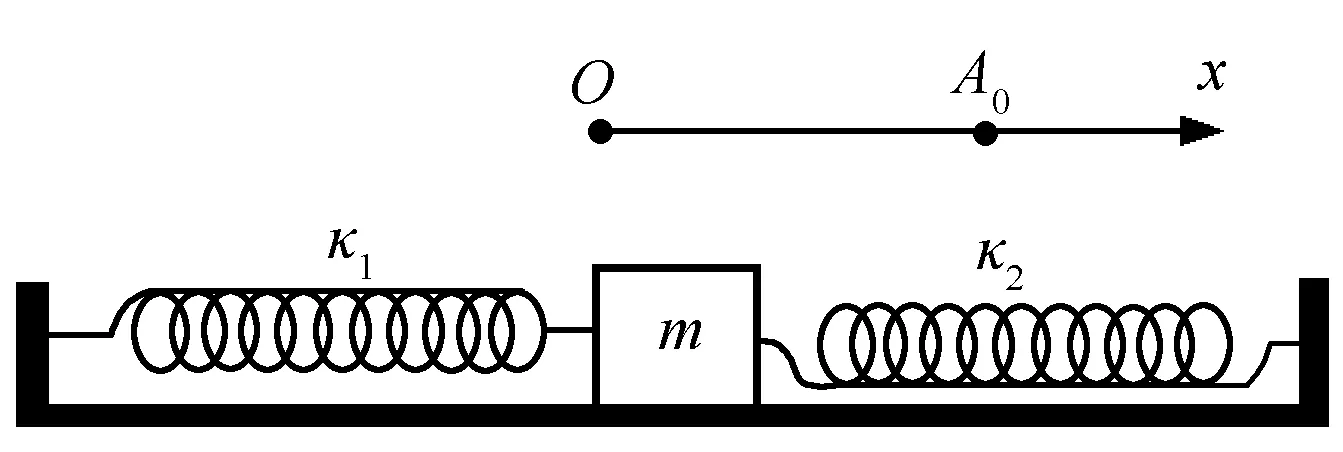
图1 气轨上滑块振动系统

1.2欠阻尼情况下的解及讨论

x=Ce-βtcos(ωft+α)

(2)

式中

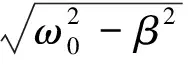
若t=0时,x=A0>0,v=0,关于C和α之间的关系可用下面两个方程来表示

A0=Ccosα

(3)

C(-β)cosα-Cωfsinα=0

(4)

联立式(3)、(4)可求得

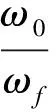
(5)

(6)

将式(5)、(6)代入式(2)可得到弹簧振子的运动学方程，表达式可写成

(7)

对式(7)两边求导可得到弹簧振子的速度方程为

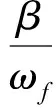
(8)

当x=0时，即

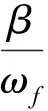
或

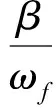
将其代入式(8)可得到平衡位置的速度，其速率方程可表示成

v1=A0ω0e-βt1

(9)

v2=A0ω0e-βt2

(10)

……

vn=A0ω0e-βtn

(11)

式(9)～(11)中v1,v2,…,vn分别表示滑块第一次、第二次……第n次经过平衡位置的速率，t1,t2，…,tn分别表示滑块第一次、第二次……第n次到达平衡位置所需的时间.由式(7)可看出，阻尼振动中的滑块每隔半个振动周期经过平衡位置一次，则式(11)可改写为

(12)

对式(12)两边分别取常用对数有

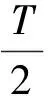
(13)

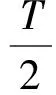
2 实验数据及数据处理

2.1实验数据

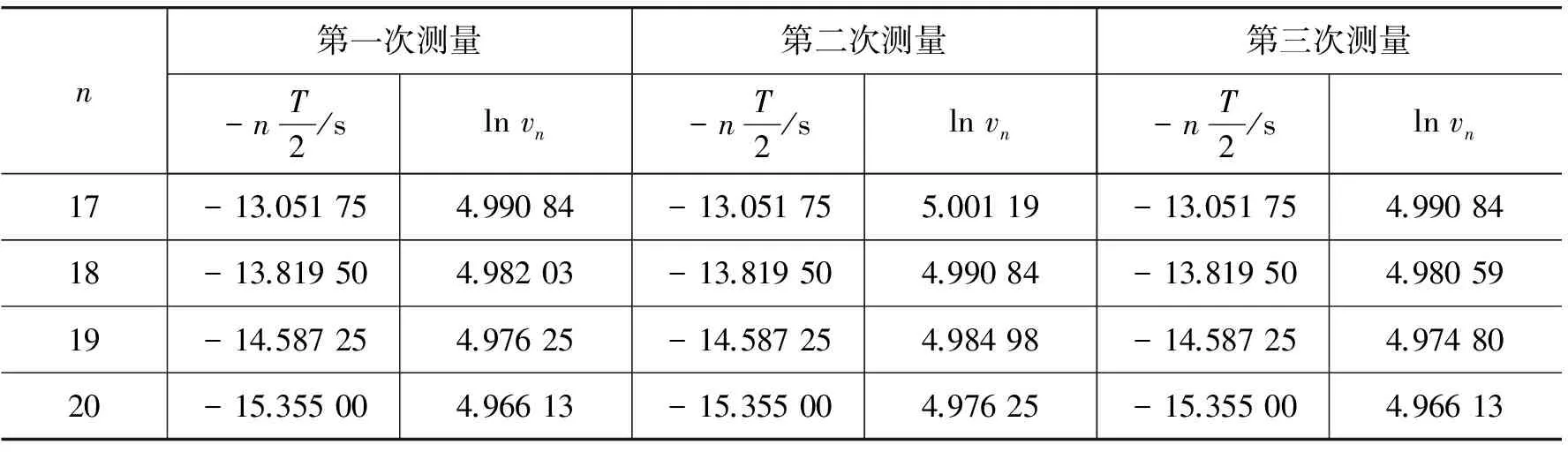
实验过程中，我们测得滑块在气轨上无阻尼作用下的平衡位置在75.97 cm处，在此处放置两个光电门，一个光电门用来测量振动周期，另一个光电门用来测量平衡位置滑块的速率.滑块静止释放位置选择在35.00 cm附近，通过数字计时计数测速仪结合两个光电门一次性测得滑块运动的周期(20个周期)和通过平衡位置的速率(20次)，共测量3次，测得实验数据如表1～3所示.

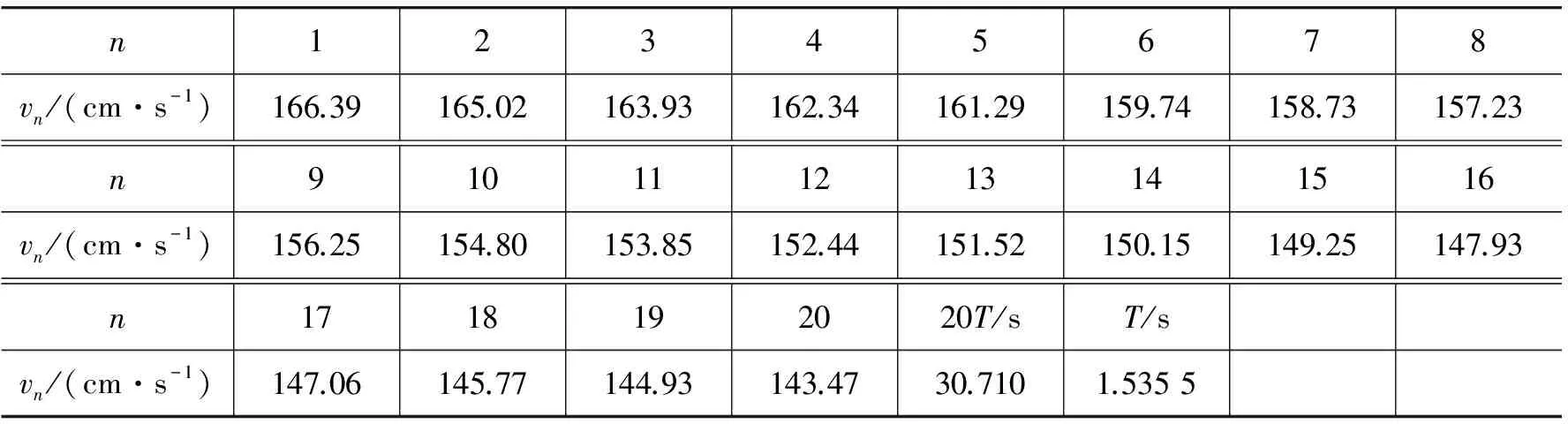
表1 滑块振动周期和经过平衡位置速率测量数据表(第一次)

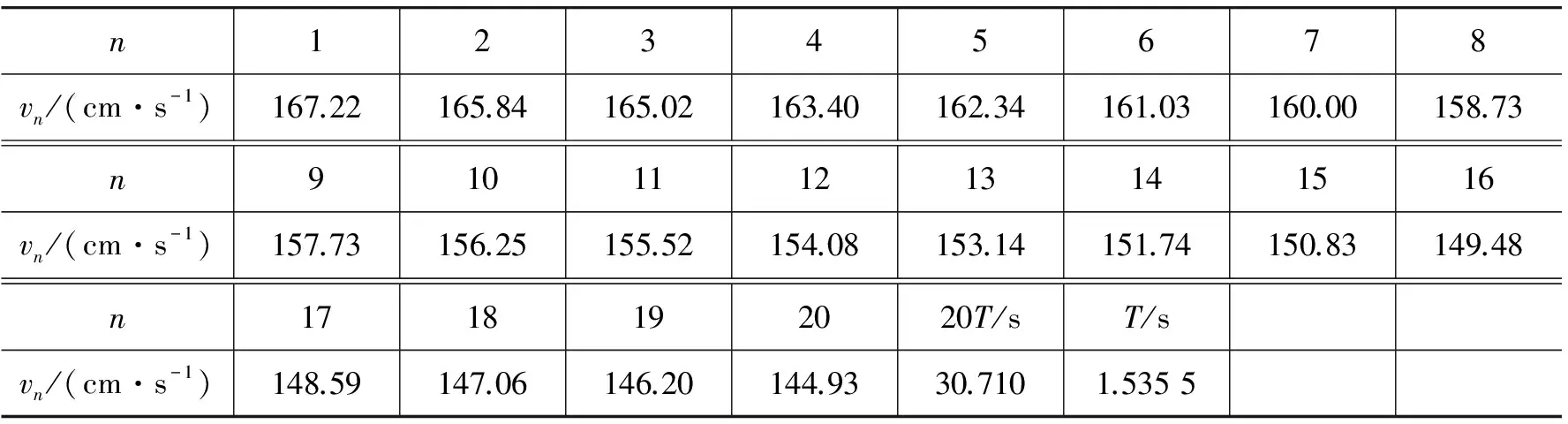
表2 滑块振动周期和经过平衡位置速率测量数据表(第二次)

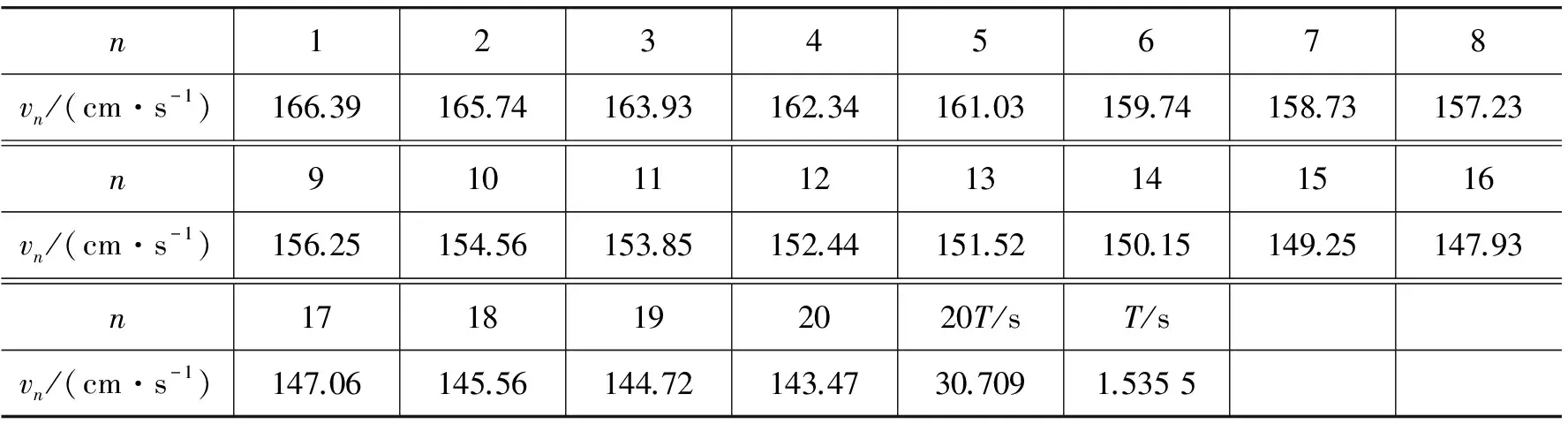
表3 滑块振动周期和经过平衡位置速率测量数据表(第三次)

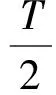
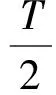
表4 -n与ln vn数值对应表

续表4

2.2数据处理

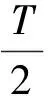
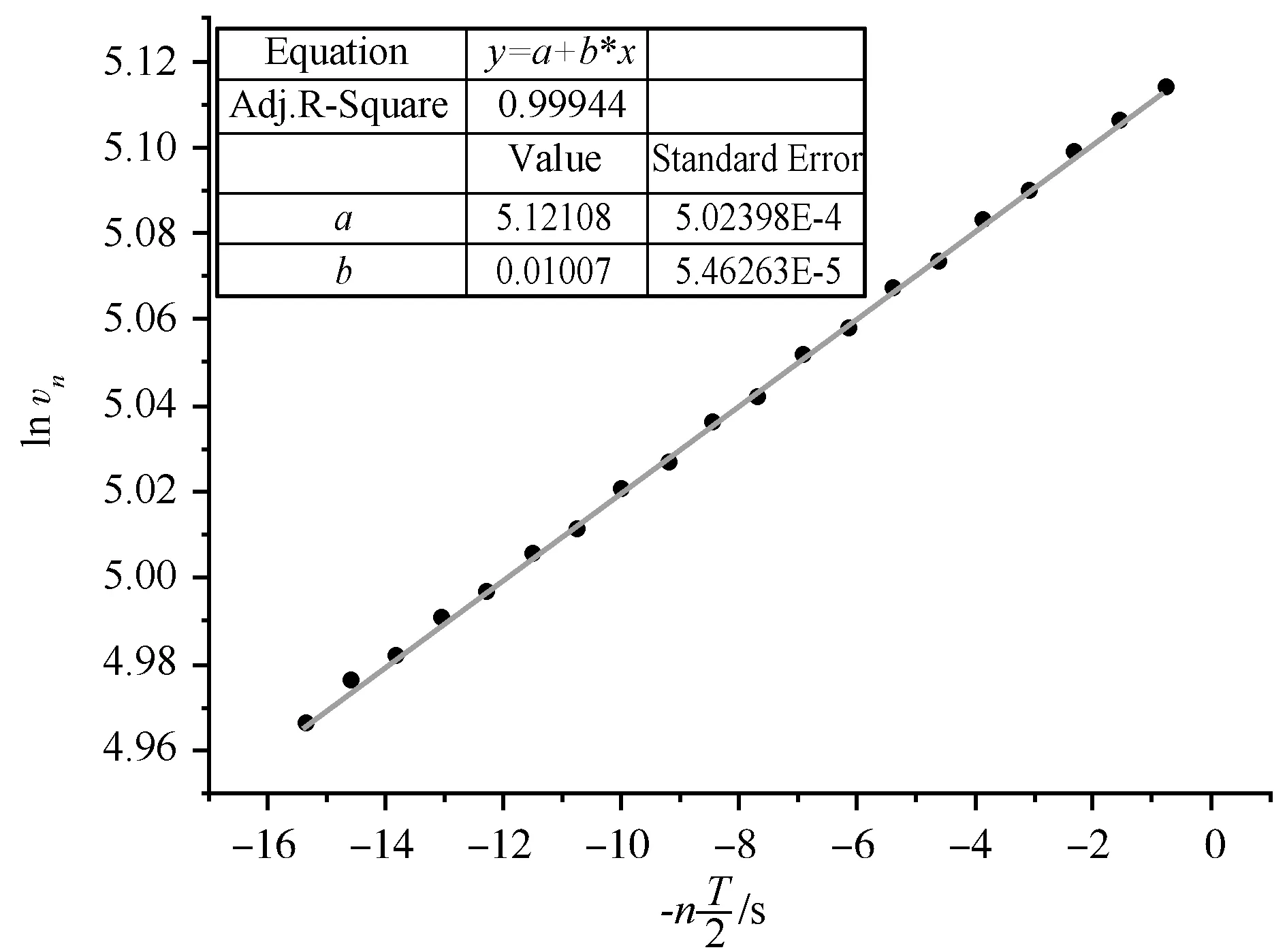
图2 ln vn与-n关系图(第一次测量)

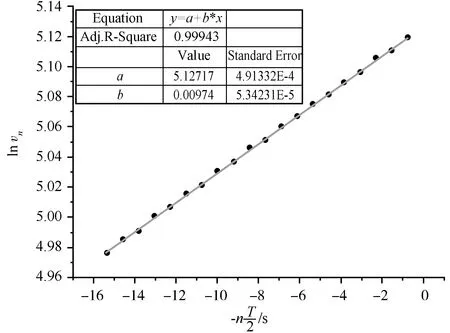
图3 ln vn与-n关系图(第二次测量)

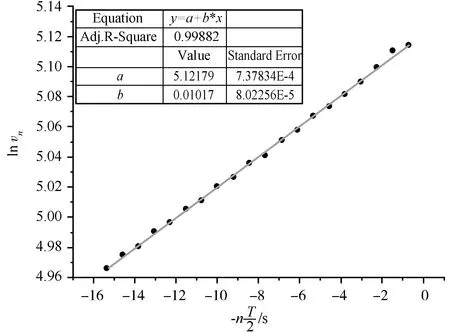
图4 ln vn与-n关系图(第三次测量)

β1=(1.007±0.005)×10-2s-1

(14)

β2=(0.974±0.005)×10-2s-1

(15)

β3=(1.017±0.008)×10-2s-1

(16)

求平均值有

β=(1.000±0.006)×10-2s-1

(17)

实验中，我们也同时测量了滑块的质量m0=171.6 g和弹簧的质量m′=13.1 g，则振子质量可表示为

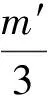
(18)

由于半衰期Th,弛豫时间τ,阻尼因数β,粘性阻尼常量γ,对数减缩λ,品质因数Q等之间满足一定的数学关系[2]，则这些振动参数可分别表示为

λ=βT=1.536×10-2

(19)

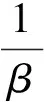
(20)

γ=2mβ=3.520×10-3kg·s-1

(21)

(22)

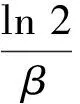
(23)

3 实验结果之间的比较

实验中，我们采取了利用Tracker软件分析气垫导轨上弹簧振子阻尼振动的方法来验证我们所提供的方法的可行性.我们在做上述3个实验时，同时进行了拍摄，利用Tracker软件如何处理视频获得实验数据，具体步骤见文献[3].图5仅给出第三组实验对应的阻尼振动部分曲线.

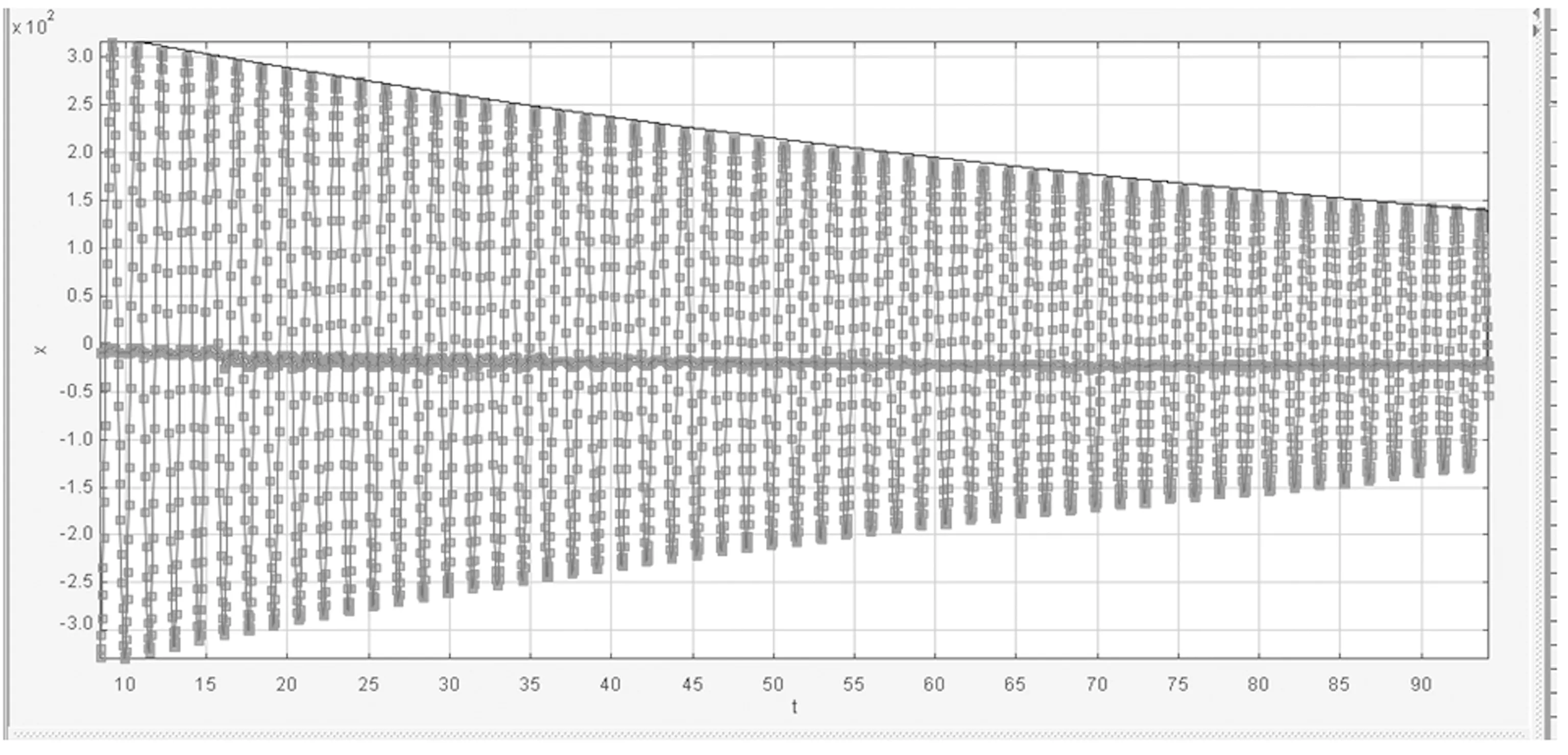
图5 阻尼振动曲线(1)

由(7)式可以看出，阻尼振动的振幅呈单指数衰减，因此，我们可用单指数函数x=Ae-βt分别拟合曲线的极大值点，图中的实线为拟合后得到的曲线.在数据处理中,我们也对上述振动曲线的极小值进行了单指数拟合，相关曲线如图6所示，两次拟合得到的参数A和β如表5所示.

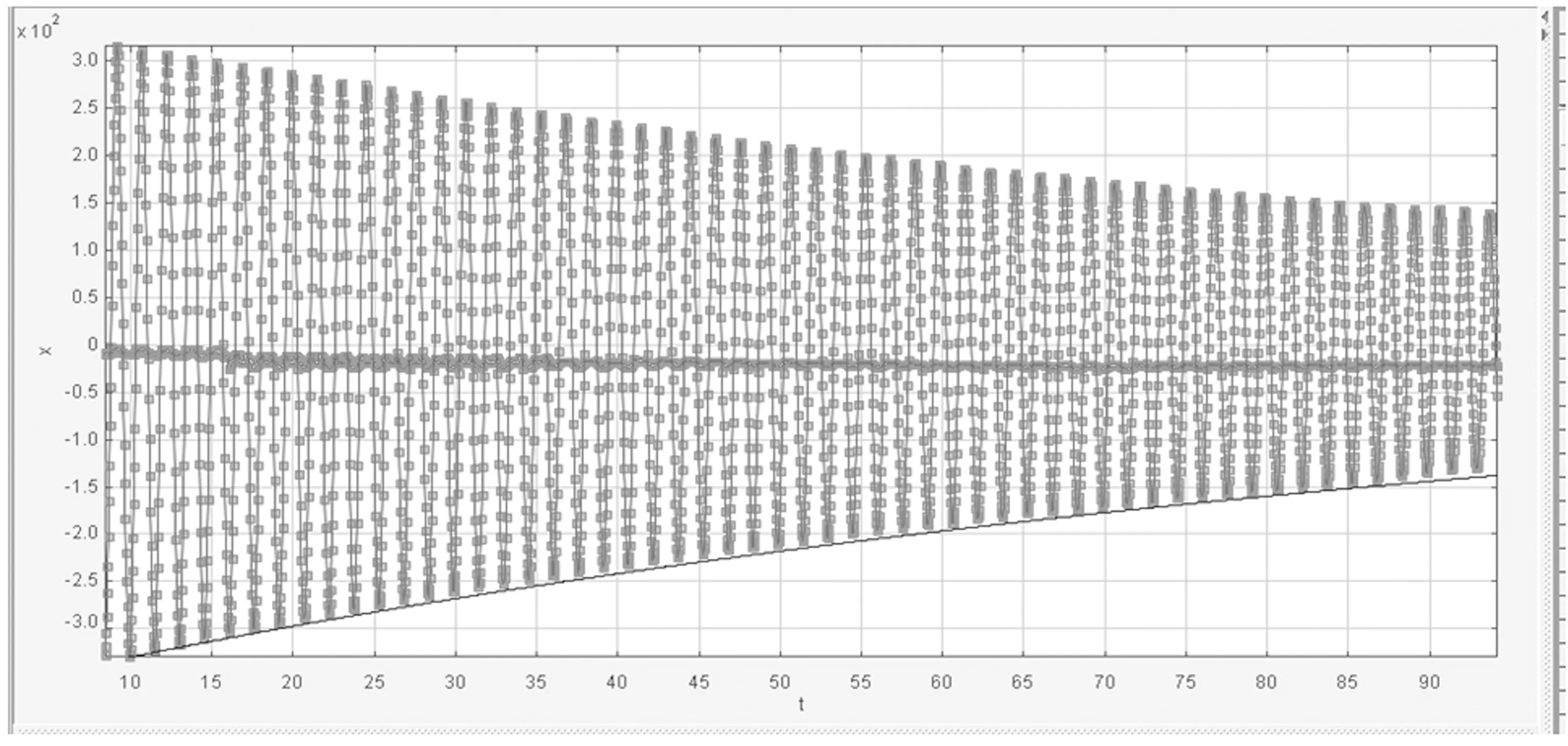
图6 阻尼振动曲线(2)

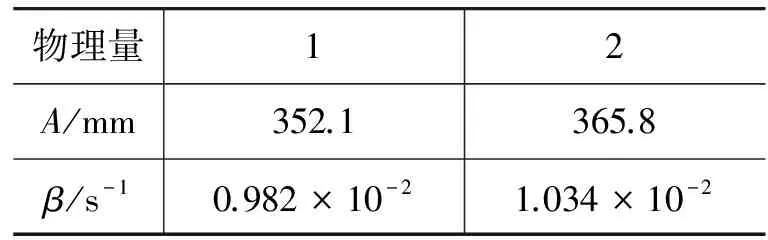
表5 振动曲线极大值和极小值单指数拟合参数记录表

根据表格提供的数据可计算出

(24)

利用振动参数之间的关系，我们可以算出其他振动参数，这里不再一一列出.结合式(17)和式(24)计算结果看出，两者结果非常接近，相对误差约为0.8%.

4 结论

实验中，用Tracker软件或火花记录仪准确测量阻尼振动曲线得到的实验结果非常可靠，但测量起来比较麻烦，实验装置也较为复杂.我们采用的实验方法主要是测量滑块通过平衡位置的速度得到相关的阻尼因数等振动参数，而利用计时计数测速仪器结合光电门测量速度非常容易，且测量效率非常高，可以一次性完成.数据处理可利用Origin软件进行直线拟合也比较简单.同时，我们将实验结果与Tracker软件法测量结果作了一下比较，两者结果的相对误差在0.8%，这些充分说明我们实验方法的可行性和可靠性.

1 方正华. 大学物理实验教程(一级).合肥：中国科技大学出版社，2014.154～155

2 杨述武，赵立竹，沈国土．普通物理实验1：力学、热学部分(第4版)．北京：高等教育出版社，2007.95～99

3 王经淘,程敏熙,贾昱,等. 利用Tracker软件分析气垫导轨上弹簧振子的阻尼振动. 大学物理，2014(4):22～24

4 钟莉,丁益民,黄娇,等. 用DIS位移传感器研究气垫导轨上的阻尼振．物理实验，2011,31(10):26～28

5 喻力华,陈昌胜,刘书龙,等. 用Matlab软件模拟振动实验. 大学物理实验, 2011, 24(3):79～81

6 姚炯,沈小娟．物理课件中阻尼振动图象的绘制．中国教育技术装备， 2008(18):70～72

MeasurementofDampingParameters

Yao Guanxin Zhang Yanhua Zeng Zongkang
(College of Physics and Electronic Information, Anhui Normal University，Wuhu，Anhui 241000)

In this paper, the relationship between the slider’s velocity in balancing position and the damping coefficient was obtained through solving differential equations and differential. A linear fit was then applied to the experimental data by using the origin software, and the damping coefficient was determined including other vibration parameters. The method was easy to operate, and the experimental data is easy to be obtained and reliable, and the processing of the experimental data is very simple.

damped vibration; vibration curve; damping coefficient

2017-03-04)

*安徽省大学物理教学团队项目，项目编号：2016jxtd049

姚关心(1973- )，男，博士，副教授，从事大学物理实验教学工作.