基于认知规律的牵连速度进阶式教学设计

杨海青(阜阳市第三中学 安徽 阜阳 236000 )

基于认知规律的牵连速度进阶式教学设计

杨海青
(阜阳市第三中学 安徽 阜阳 236000 )

在处理绳、杆的牵连速度教学时，基于学生的心理认知规律，多视角构建物理模型，进阶式选取研讨例题，实现学生对本问题的融会贯通，而又引发学生思考，留下思维进阶空间，立足智慧教学，培养学生的学习、探究力.

认知规律 牵连速度 学习进阶 教学思考

物体通过绳(杆)来连接，由于研究对象的运动方向和绳(杆)不在一条直线上，因此速度常常是不同的，这种问题即为牵连速度问题.这类问题是“运动的合成与分解”中非常典型的物理模型，但是因为规律的隐含性，很多学生存在心理认知障碍，甚至对问题产生畏惧感，如若能很好地建构模型，不仅可以帮助理解模型的物理特点和运动规律，还可以提高学生的学习认知能力，在物理教学上是一件很有意义的事情.

1 多维视角 构建模型

1.1展现历史及生活场景创设问题情境

展示历史资料及生活照片，创设问题情境，如图1所示.

图1 以历史资料及生活照片为资源，创设问题情境

意图简析：以历史的著名图片和生活照片为探究资源，创建问题化的教学情境，使学生的认知有情境感，符合学生的心理认知规律.历史名图的使用，使物理课堂更具文化感，更厚重，更符合核心素养下的物理教学理念；生活化的图片使物理教学更具亲切感，更具时代感.双重图片的使用，能引发学生从物理学科视角对历史问题、生活问题的关注与思考，使学生更有时代使命感和强烈的问题意识.

由历史名图、生活照片到物理图片再到物理问题的语言表征，由情景化到问题化，物理问题逐步明晰，多元表征，为问题的解决和物理模型的建立作思维认知定向.

1.2分析方法

1.2.1 宏观——效果分解法[1]

应用物体实际运动效果来分解，取物体和绳的连接点为研究对象，研究对象的实际运动为合运动，方向沿水平面向左，从运动的效果上看，研究对象同时参与了两个方向的运动：沿绳方向的收缩运动，绕以滑轮相切点为旋转点的圆周运动.所以合速度应沿着绳的方向和垂直于绳的方向进行分解，如图2所示.所以

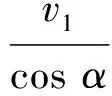
模型得建.

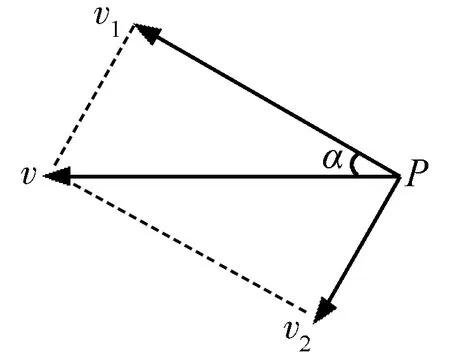
图2 效果分解法分析图

1.2.2 微观——微元极限法

设从该时刻起经过时间Δt，小船从A位置沿水平面向左行驶到C位置，滑轮右侧的绳缩短了Δx1，如图3所示.当时间极短时，△ABC可近似看成直角三角形，所以

Δx1=Δxcosα

由数学推演得

由速度的定义，等式的物理含义就是

v1=vcosα

故有

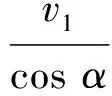
模型得建.

图3 微元极限法分析图

1.2.3 守恒观——能量守恒功率法

师生研讨评析：方法一是基本方法，也是高中阶段很常规、最常用的方法，学生易于掌握，具有推广价值.方法二最本质，是思想方法类的，能引发学生对速度的深层次思考，从微观的视角出发，回归到瞬时速度的物理本质，实现对合速度的分解，最大的价值在于对学生思维方式的启迪.方法三，以守恒的观念、从能量的视角建构，基于深度理解绳的物理属性，对牵连速度的高境界处理，能彰显学生的物理功力.此方法宜在高三一轮复习时研讨，进阶式处理，易于学生对知识融会贯通，深度学习.这类问题的物理本质是理想化的绳杆模型，即具有这样的物理属性：动力属性绳不可伸长，杆不可伸长和压缩且是无质量的，是轻质的；能量属性能传递能量，自身不储存能量.综合比较，教学上立足智慧教学，启迪学生思维，多角度构建物理模型.

2 进阶式教学设计

2.1绳子一端固定一端运动

【例1】如图4所示，一块橡皮用细线悬挂于O点，用铅笔靠着线的左侧水平向右匀速移动，运动中始终保持悬线竖直且悬线总长度不变，则橡皮运动的速度( )

图4 例1题图

A．大小和方向均不变

B．大小不变，方向改变

C．大小改变，方向不变

D．大小和方向均改变

进阶题1.1：如图5所示，一块橡皮用细线悬挂于O点，现用一支铅笔贴着细线的左侧水平向右以速度v匀速移动，运动过程中保持铅笔的高度不变，悬挂橡皮的那段细线保持竖直，则在铅笔碰到橡皮前，橡皮的运动情况是( )

A．橡皮在水平方向上做匀速运动

B．橡皮在竖直方向上做加速运动

C．橡皮的运动轨迹是一条直线

图5 进阶题1.1题图

进阶题1.2：如图6所示，一块橡皮用细线悬挂于O点，用钉子靠着线的左侧，沿与水平方向成30°的斜面向右以速度v匀速运动，运动中始终保持悬线竖直，则橡皮运动的速度( )

图6 进阶题1.2题图

A.大小为v，方向不变和水平方向成60°

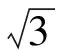
C.大小为2v，方向不变和水平方向成60°

D.大小和方向都会改变

进阶题1.3：如图7所示，斜面体A的倾角为θ，其顶点有一小定滑轮B，绕过定滑轮的细线的一端固定在竖直墙面上C点，B，C间细绳水平，细绳另一端与置于斜面底端的小球D相连，现推动斜面体以速度v匀速向右运动，则下列说法正确的是( )

图7 进阶题1.3题图

A.小球D做匀速直线运动

B.小球D做变速曲线运动

D.小球D的速度方向垂直斜面向上

2.2绳子两端物体都运动

【例2】如图8所示，某人用绳通过定滑轮拉小船，设人匀速拉绳的速度为v0，小船水平向左运动，绳某时刻与水平方向夹角为α，则小船的运动性质及此时刻小船的速度vx为( )

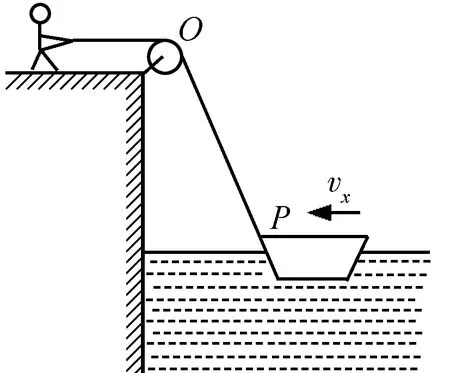
图8 例2题图

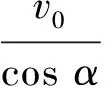
B．小船做变加速运动，vx=v0cosα

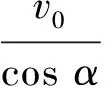
D．小船做匀速直线运动，vx=v0cosα

进阶题2.1：如图9所示，做匀速直线运动的汽车A通过一根绕过定滑轮的长绳吊起一重物B，设重物和汽车的速度大小分别为vB和vA，则( )

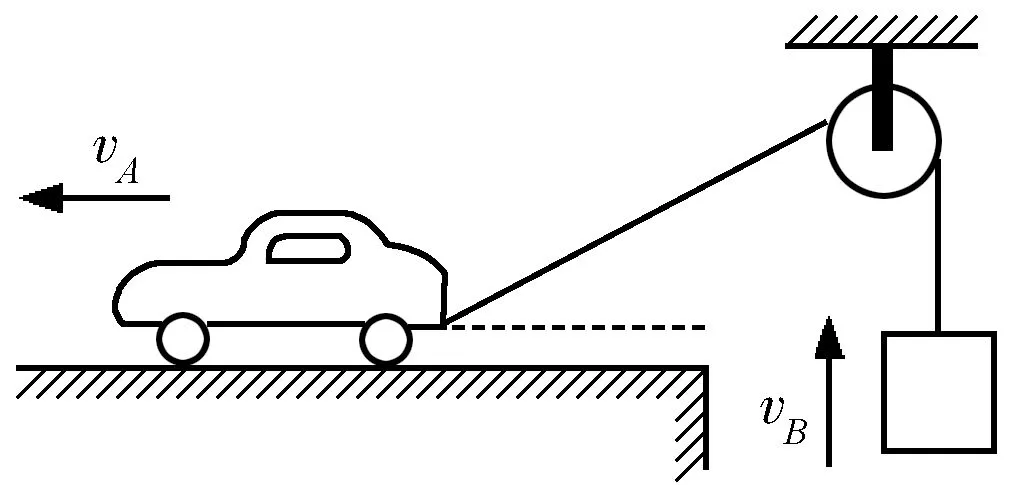
图9 进阶题2.1题图

A．vA=vB

B．vA

C．vA>vB

D．重物B的速度逐渐增大

进阶式追问：请同学们思考，重物B也做匀速直线运动吗？绳子对重物B的拉力与重物B的重力有什么关系？重物B处于什么状态？汽车继续匀速运动，则绳子对重物B的拉力如何变化？

进阶题2.2：如图10所示，在不计滑轮摩擦和绳子质量的条件下，当小车以速度v匀速向右运动到如图所示位置时，物体P的速度为( )

图10 进阶题2.2题图

A．vB．vcosθ

2.3绳子和杆组合

【例3】人用绳子通过定滑轮拉物体A，A穿在光滑的竖直杆上，当以速度v0匀速地拉绳使物体A到达如图11所示位置时，绳与竖直杆的夹角为θ，则物体A实际运动的速度是( )

图11 例3题图

进阶式追问：物体A上升至与定滑轮的连线处于水平位置时，其上升速度v≠0，求这时B的速度v0大小为多少？

进阶题3.1：如图12所示，重物M沿竖直杆下滑，并通过绳带动小车沿斜面升高．当滑轮右侧的绳与竖直方向成θ角，且重物下滑的速率为v时，小车的速度为( )

图12 进阶题3.1题图

进阶式追问：若重物M匀速下滑．设绳子的张力为FT，在此后的运动过程中，小车的运动性质是什么？张力FT和小车的重力下滑分力有什么关系？

进阶题3.2：如图13所示，有一个直角支架AOB，OA水平放置，OB竖直向下，OA上套有小环P，OB上套有小环Q，两环间由一根质量不计不可伸长的细绳相连，小环P受水平向右外力作用使其匀速向右平动，在P平动过程中，关于Q的运动情况以下说法正确的是( )

图13 进阶题3.2题图

A．Q匀速上升

B．Q减速上升

C．Q匀加速上升

D．Q变加速上升

3 师生研讨 思维升华

绳、杆等连接的两个物体在运动过程中，其速度通常是不一样的，但两者的速度是有联系的(一般两个物体沿绳或杆方向的速度大小相等)，我们称之为“牵连”速度．解决此类问题的一般步骤如下：

第一步，先确定合运动，物体的实际运动就是合运动；

第二步，确定合运动的两个实际作用效果，一是沿牵引方向的平动效果，改变速度的大小；二是沿垂直于牵引方向的转动效果，改变速度的方向；

第三步，按平行四边形定则进行分解，作好运动矢量图；

第四步，根据沿绳(或杆)牵引方向的速度相等列方程．

1 杨榕楠.更高更妙的物理——高考高分与自主招生决胜篇．杭州：浙江大学出版社，2013.52

2017-03-24)