基于面板数据分位数回归的商品住宅价格影响因素分析

赵 强，曹炜婷

(南京财经大学公共管理学院，江苏南京 210023)

基于面板数据分位数回归的商品住宅价格影响因素分析

赵 强，曹炜婷

(南京财经大学公共管理学院，江苏南京 210023)

构建全国35个大中城市2005－2014年的面板数据，基于供给需求理论，应用分位数回归的方法剖析房地产价格的影响要素。研究结果发现，人均可支配收入和人均GDP在各分位点上的系数都显著为正，并且人均可支配收入在各分位点上大体呈现出一种上升的趋势，而人均GDP则呈现出下降的态势。总人口在0.25和0.5这两个分位点上对商品住宅的平均销售价格是有显著正向影响的。相反地，商品住宅投资完成额在0.25和0.5这两个分位点上呈现出显著的负向影响。单位面积房屋竣工造价在0.75和0.9这样的高分位点上是不显著的。人均可支配收入在众多影响因素中对房价的影响作用是最大的，而其对高房价的影响又比低房价更大，这也说明了在我国高房价的城市对于购买者的收入要求较高。

住宅价格；面板数据；分位数回归；供给需求理论

0 引 言

住房价格的影响因素是房地产经济学和房地产管理学研究的重要问题。目前，国内外学界对于住房价格的研究主要采用两种方法:一种是以特征价格模型为基础的研究方法，这是一种传统的经典的研究方法；另一种是近年来兴起的分位数回归方法。特征价格模型方法[1]属于住房价格的微观研究方法，适宜于研究具体的住房小区或建筑，主要通过构建区位特征、邻里特征和环境特征三个维度的自变量，通过多元回归模型的方法来揭示住房价格的影响因素及其大小和方向。而分位数回归方法则通过划分不同的分位点，来解释各影响因素在不同的分位点上对住房价格影响的不同效应。由于分位数回归方法在我国的住房价格研究中才刚刚兴起，现有的研究成果还较少，需要更多的实证研究成果来检验该方法在住房价格研究中的应用效果，因此，本文拟基于全国35个大中城市房价的面板数据，应用该方法，研究商品住宅价格的影响因素，并且分析各影响因素在不同分位点上对房价影响效应的差异。

1 文献综述

住房价格的影响因素是房地产经济学界持续关注的热点问题。总结起来看，学者们主要围绕以下问题进行探讨:影响住房价格的因素有哪些?这些因素如何影响住房价格?在对这些问题的研究中，学界提出了一种经典的模型即特征价格模型，该模型把住房价格的影响因素分为三类即区位特征、邻里特征和环境特征。该方法已经广泛应用于西方国家的住房价格研究中，也在我国学界对住房价格的研究中广为采用。

由于经典的特征价格模型主要针对的是微观的住房市场分析，在扩展到以城市为分析单位的住房价格研究中具有局限性，因此，在对城市的房价研究中学者们又提出了其他的住房价格影响因素。刘在军[2]选取北京上海广州深圳这四个国内重点城市商品住宅市场2006－2008年的数据进行回归分析。研究发现，主要成本、人口因素对商品住宅价格的影响显著，其次是房地产开发投资、平均收入因素，相对而言人均GDP增长率对商品住宅价格的影响较弱。张晶等[3]首先验证了美国的房地产价格与利率变动之间存在着长期的反向关系，然后选取我国2000年第1季度到2010年第2季度的数据，得出这一关系在中国也存在。实证结果发现，利率对于房价具有较明显的影响，此外，消费价格指数、居民收入、商品房竣工面积的变动值对房价的影响程度更大。同时，在对以城市为单位的住房价格研究中，也广泛采用了面板数据方法，如廖阳等[4]对西安、重庆、成都等7个西部中心城市2002－2008年的商品住宅价格采用面板数据模型进行研究。结果表明，城镇居民可支配收入水平、商品住宅竣工面积和GDP对商品住宅价格有着重要的影响作用。在分析的计量方法上，也有学者采用自回归模型，如王泳茹[5]选取2011.2－2015.7全国的月度数据，建立自回归模型，分析住房市场的供给和需求与房价之间的动态关系。结果表明，在住房市场中，需求对其的影响是积极的，供给表现出的影响是消极，且就影响程度而言需求大于供给。

近年来，在国外的住房市场研究中，兴起了一种新的计量方法，即分位数回归模型，这种方法可以揭示在不同的分位点上各个影响因素对住房价格影响效应的差异，比传统的研究方法具有一定的优点。我国学界也已开始应用该方法于房地产市场研究中。这种方法的应用中，常常以面板数据为基础。如李顺毅[6]选取2005－2009年中国省级面板数据，结合分位数回归，分析了房价是如何影响消费对经济增长的贡献率的。研究发现，无论是在哪个分位点上，房价对消费贡献率的作用都表现出倒U形状，而且分位点越高，与之对应的倒U曲线的拐点所对应的房价就越高。同时，加大货币供应量会促进房价对消费贡献率的正向影响，而削弱负向影响。罗玉波[7]运用分位数回归方法探讨了住宅特征对于其价格的影响，结果发现，不同的分位数水平上，各个特征要素对于房屋售价的影响程度不同，从而全面描述了不同特征要素对房屋售价的影响。

分位数回归模型和面板数据相结合，形成了房地产市场研究中的面板数据分位数回归的新的发展趋势。林勇等[8]选用全国311个城市2005－2012年的数据，应用面板分位数回归模型深入地探讨了我国房地产市场的财富效应。研究结果发现，就整体而言，房价对城镇居民消费具有显著的弱财富效应，但就分地区而言，各地区之间的影响程度有所不同且相差较大。利用聚类分析法将所有城市分为五线，房价对不同线的城市居民的消费影响作用不同。对一线城市表现出弱挤出效应；对二、三、五线城市表现为弱财富效应；对四线城市则表现为较为显著的财富效应。此外还发现，城镇居民消费的关键要素仍然是人均可支配收入，提高社会保障水平能够明显的推动中低收入人群的消费，且提升城镇化水平也有助于城镇居民增加消费。张所地等[9]选用35个大中城市1999－2011年的面板数据，选用面板分位数回归的方法研究收入、利率对房价的影响作用。结果发现，收入是影响房价上涨的主要因素而非成本，利率变动对房价的影响并不明显；各影响因素在不同分位点水平下的影响程度具有较大的差异，当城市的房价水平越高，房价受收入影响的作用就越大，而受成本、人均GDP等因素的影响就会越小。林海波等[10]等基于2000－2010年的相关数据，利用分位数面板模型，初次探讨移民教育水平和房地产价格之间的关系。结论表明，促使房价上涨的主要移民力量是蓝领或小工商业者，而不是一些高学历的移民。然而房价的持续走高对于移民尤其是大学生而言，并没有成为他们很大的障碍，教育和创业可以让受教育程度高的移民愈加顺应当地经济的升级变迁，融入迁入地。

为了进一步拓展分位数回归模型在房价研究中应用，本文构建了2005－2014年中国35个大中城市的面板数据，运用分位数回归的方法来研究商品住房价格的影响因素。由于分位数回归能够更加详细的反映整个条件分布的全貌，不容易受极端值的影响，所以它不仅能反映出各个影响因素对商品住宅价格的作用，还能详细分析出影响因素在不同分位数水平上对房价的影响作用的差异。

2 分位数回归的基本原理

在传统的回归模型中，我们通常着重关注的是自变量x对因变量y的条件期望E(y｜x)的影响，这实际上是均值回归。但如果条件分布y｜x不是对称分布，则条件期望难以反映整个条件分布的面貌。为了能对条件分布y｜x有一个全面的了解，Koenker和Bassett提出了分位数回归，能够估计出条件分布y｜x的一些重要的条件分位数，如中位数、1/4分位数、3/4分位数等。另一方面，分位数回归把残差绝对值的加权平均(如，)当作最小化的目标函数，解决了均值回归中容易受极端值影响的问题，较为稳定。

分位数回归模型[11]的基本思想可以描绘为:假定连续随机变量Y，它的累积分布函数是Fy(·)，则Y的“总体q分位数”记作yq，有表达式:q＝P(Y≤yq)＝Fy(yq)。即yq正好将总体分布一拆为二，其中小于等于yq的概率为q，反之大于yq的概率为(1－q)。假定q＝0.5，则为中位数，将总体恰好分成两等分，一半在中位数之上而另一半则在中位数之下。

对于回归模型而言，把条件分布y｜x的累积分布函数记为Fy｜x(·)。条件分布y｜x的总体q分位数记作yq，有此表达式:q＝Fy｜x(yq)。设定条件分位数函数是关于自变量x的线性函数，即，其中 βq是q分位数回归下的系数，其估计量可以使用最小化问题来进行定义，如下:

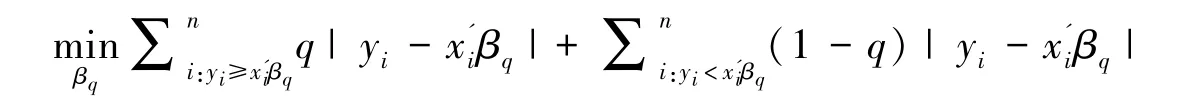
因为分位数回归的目标函数上有绝对值，不能够进行微分，所以可以利用线性规划来计算。

3 数据来源与实证模型

3.1 模型设定

由于能够巧妙地处理遗漏变量问题，能提供更多个体变动行为的信息，提高估计的精确度，面板数据的应用越发广泛。经典的面板数据模型主要有以下三种(见表1):

表1 面板数据模型的主要类型

在本文中，因变量y就是商品住宅的平均销售价格，自变量x代表房价影响因素的向量。本文在选择模型时，可以通过进行F检验、LM拉格朗日乘子检验以及豪斯曼(Hausman)检验，来确定最终模型。

3.2 指标选取

住宅是一种商品，其价格的形成是由供给和需求两方面所确定的。因此，本文在选择影响房价的因素时主要是基于“需求－供给”的框架。参考已有的研究成果，本文选取如下影响因素:

从需求层面出发，主要考虑总人口、人均可支配收入、人均GDP这三个影响因素。总人口[12]是住房需求的影响变量，人口规模的增加很可能会导致住房市场需求的增加，最终会导致住房价格的上涨。人均可支配收入[13]是购买力的直接体现，是将住房的潜在需求转换为实际需求的重要指标。人均可支配收入的增加提高了购买者的支付能力，进而增加住房需求，最终导致房价上涨。人均GDP[14]是经济发展水平的直接体现，一般而言，经济发展水平较高的地方，投资需求就高，包括对房地产的投资需求，最终导致房价上涨。

从供给层面上看，主要考虑房地产投资完成额、房屋销售面积、房屋竣工造价这三个影响因素。房地产投资完成额[15]越多，对住房市场的促进就越大，同时也说明住房需求在增加，短期内会推动房价上涨。但长期来看当住房的投入大于需求时，住房价格又会下降。房屋销售面积越大，表明市场对住房的需求越大，最终导致房价上涨。房屋竣工造价[16]反映了住房建造成本，成本增加必然会导致房价的上涨。

此外，还有同时对住宅供给和需求产生影响的利率因素[17]。一方面，房地产市场对于资金的需求量大，当利率升高时，房地产开发商融资成本加大，房地产投资缺乏吸引力，住房市场供给下降。另一方面，当利率升高时，购买者的资金利息成本也加大，住房市场需求也会下降，最终导致房价发生变动。表2详细说明了本文所使用的变量。

表2 主要变量的说明

现在利用经典的供给需求曲线从理论上来分析本文所选7个指标的变化是如何影响到住宅价格的。如下图1所示，需求曲线D，供给曲线S。譬如，当总人口、人均可支配收入、人均GDP上涨时，即需求增加，需求曲线从D右移到D1，此时假设供给不变，其他条件也保持不变，房价、交易量都会上涨。当房地产投资完成额和房屋销售面积增加，单位面积房屋竣工造价下降时，就会导致房地产市场的供给增加，即供给曲线从S右移到S1，若保持需求不变，此时供过于求，房价下降。

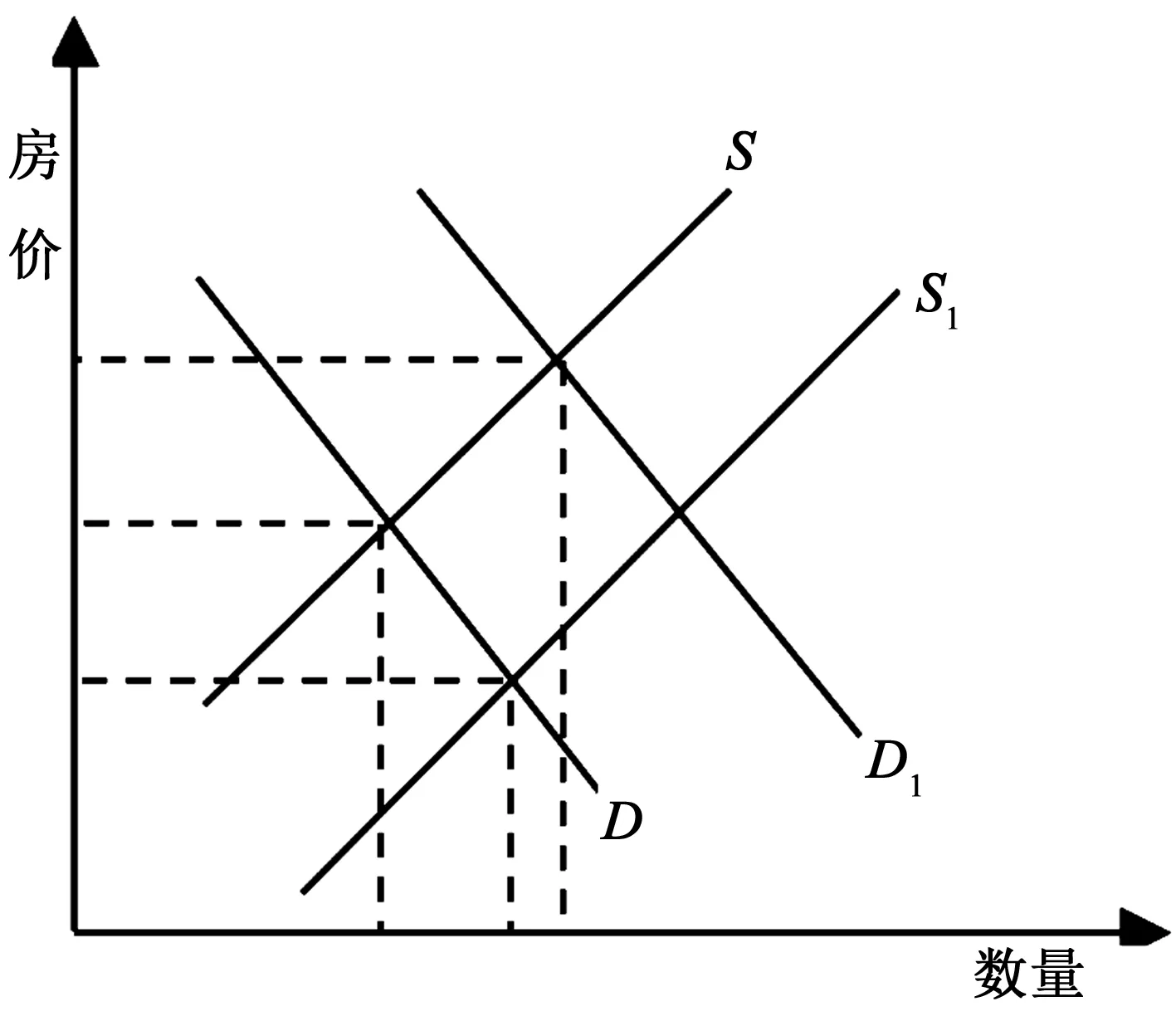
图1 商品住宅供给需求曲线

3.3 数据说明及其描述性统计

本文构建2005－2014年中国35个大中城市的面板数据进行分析，其中总人口、人均可支配收入、人均GDP、商品住宅投资完成额、单位面积房屋竣工造价、商品住宅平均销售面积、商品住宅平均销售价格数据均来自历年的《中国统计年鉴》，5年以上贷款利率来自中国人民银行网站(http://www.pbc.gov.cn/)。需要说明的是，贷款利率在有些年份内被多次调整，本文用其均值替代，并利用相应的通货膨胀率平减转化为实际贷款利率。以2005年为基期，人均可支配收入、商品住宅平均销售价格以及房屋竣工造价的数据都采用CPI指数进行了价格平减；人均GDP的数据采用了GDP平减指数进行价格平减；商品住宅投资完成额的数据采用固定资产投资价格指数也进行了价格平减，为实际值。为了消除异方差的影响，本文将所有的变量都做取自然对数处理。表3反映了各主要变量的描述性统计特征。

表3 主要变量的描述性统计

4 实证研究结果分析

4.1 数据平稳性检验及协整检验

为防止出现伪回归，在参数估计之前首先要对数据进行平稳性检验，即单位根检验。面板单位根检验的方法有很多种，如同质面板数据的LLC检验、HT检验、Breitung检验以及异质面板数据的IPS检验、Fisher－ADF检验和Fisher－PP检验。为防止单一检验可能造成的误差，本文利用Stata12.0软件，选取其中的三种检验方法进行平稳性检验，检验结果见下表4。

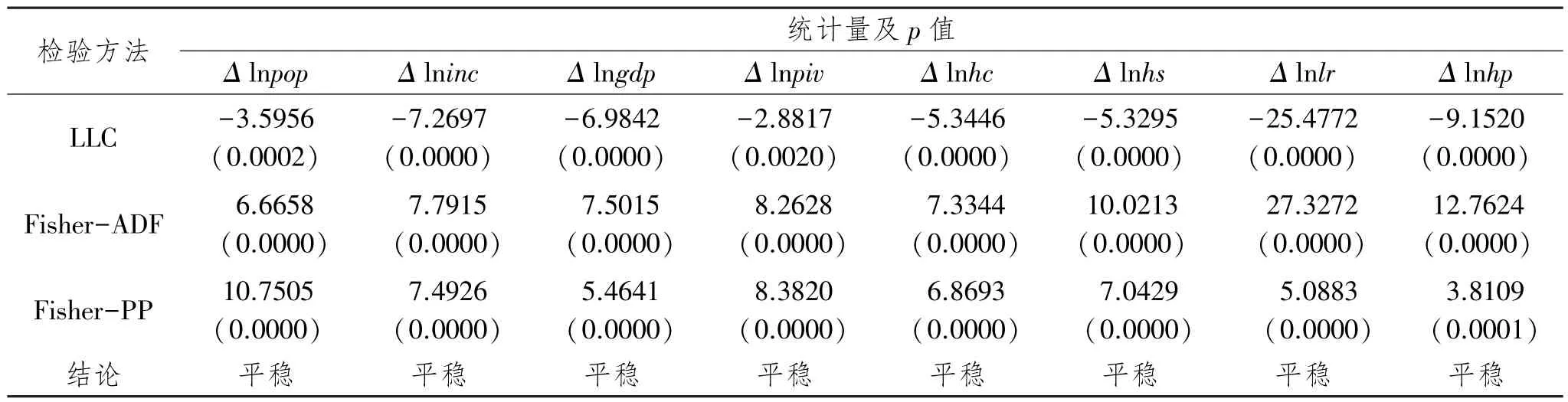
表4 单位根检验结果

从上表的检验结果可以看出，原序列的对数序列都显示是非平稳的。而其一阶差分序列如上表所示可以强烈拒绝包含单位根的原假设，故可认为一阶差分序列是平稳的，原序列的对数序列均为I(1)，即一阶单整。

在满足一阶单整的条件下，接下来要对商品住宅平均销售价格在内的所有变量做协整检验。面板数据协整性检验方法有Pedroni、Kao、Fisher检验三种。本文首先利用Pedroni方法对所有变量进行协整检验，结果发现变量之间并不存在协整关系，于是本文将变量进行多种剔除组合再代入进行协整检验，结果发现当同时剔除贷款利率的对数lnlr和商品住宅平均销售面积的对数lnhs这两个变量时，剩余的变量存在明显的协整关系。为此本文还采用了Kao检验进行验证，检验结果见表5，ADF的统计量很显著，拒绝没有协整关系的原假设。因此本文在下面的面板数据模型和分位数回归的分析中删除lnlr和lnhs这两个扰乱协整关系的变量。

表5 基于Kao检验的协整检验结果

4.2 面板数据模型选择

在模型设定中本文已经分析了面板数据的三种经典模型，每种模型的适用性都是有差异的，本文究竟选择哪种模型进行分析可以通过F检验、LM拉格朗日乘子检验以及豪斯曼(Hausman)检验来加以确定，检验结果见表6。

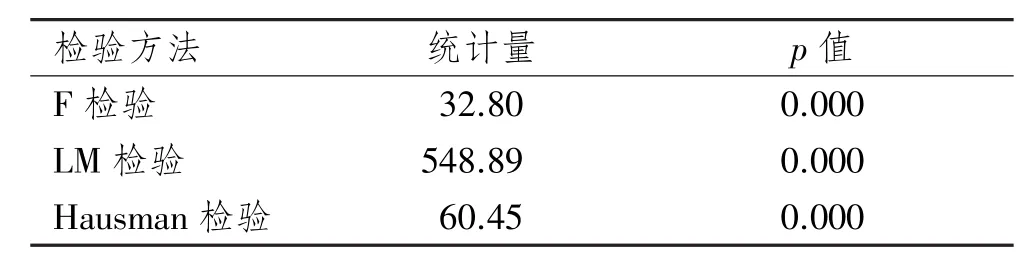
表6 面板数据模型选择检验结果

分析表6的检验结果，F检验的p值为0.000，故在1%的显著性水平下，强烈拒绝“每个个体的常数项都相等”的原假设，认为固定效应模型要明显优于混合回归模型；LM检验的p值为0.000，故在1%的显著水平下，强烈拒绝“不存在个体随机效应”的原假设，认为在随机效应和混合回归两者之间应该要选择随机效应；Hausman检验的p值也是0.000，故在1%的显著性水平下，拒绝“误差项与解释变量不相关”的原假设，则模型最终应该设定为固定效应而非随机效应。

4.3 分位数回归

传统的固定效应面板数据模型固然是可以反映商品住宅价格与其影响因素之间的关系，但是为了详细分析商品住宅价格的影响因素对其不同价位的影响是否有差异，本文接下来又选用了分位数回归的方法进行研究。在此选择了比较有代表性的0.1，0.25，0.5，0.75，0.9这五个分位点，分别代表低房价、中低房价、中等房价、中高房价以及高房价。将35个大中城市的面板数据分别代入这两种模型中，并利用stata12.0软件分别运行面板数据固定效应模型和分位数回归命令进行估计，结果列于表7中。为了能够更加直观的观察分位数回归系数随着分位点的变化情形，将各自变量随着分位点的变化绘制在图2中。

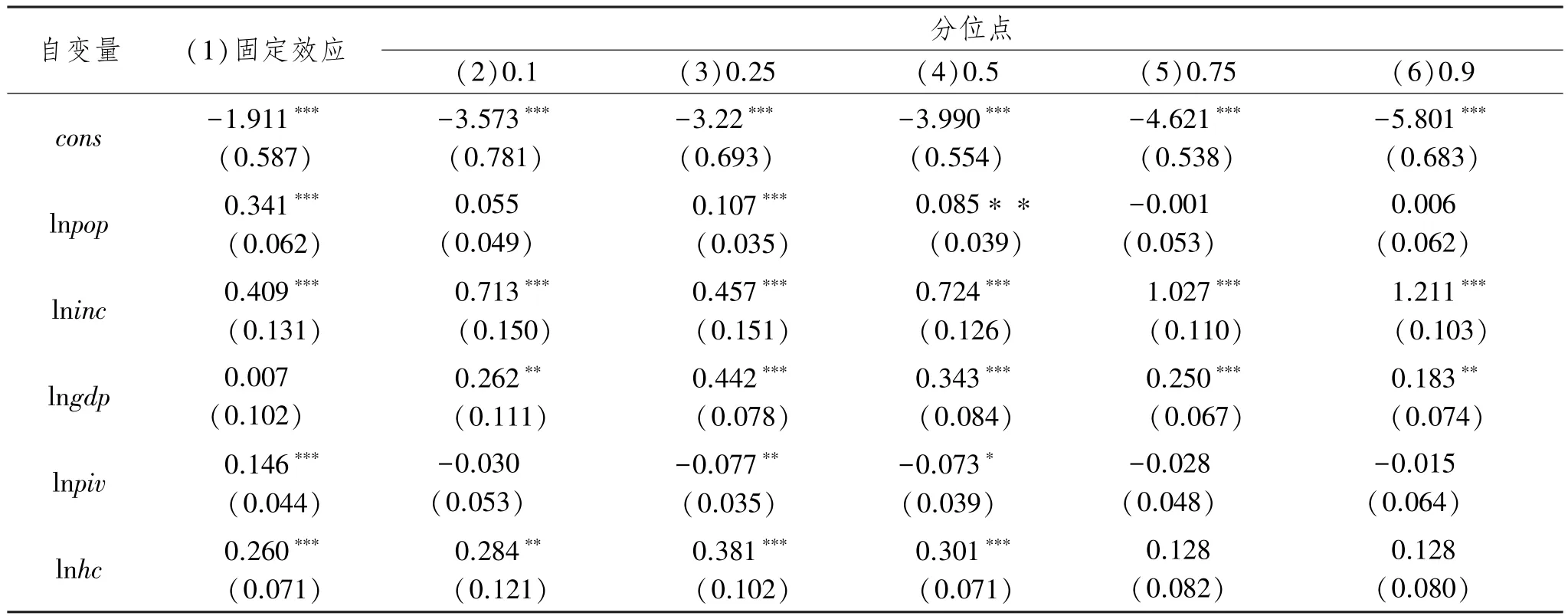
表7 面板数据分位数回归估计结果

观察表7可以看出，面板数据的固定效应模型与分位数回归方法得出的系数的符号大体一致，但是在分位数回归的结果中，我们可观察到在不同的分位点下，各影响因素对房价的影响有差异并呈现出一定的规律，这是在固定效应模型中无法观测到的信息。

第一，表中第(1)列呈现的是固定效应模型的结果，观察发现，除了人均GDP(lngdp)，其余变量都通过了1%显著性水平下的统计检验，且系数都为正，说明这些因素对商品住宅价格有显著的正向影响。其中人均可支配收入(lninc)的弹性系数最大为0.409，其次是总人口(lnpop)变量为0.341，这两个影响因素的增加通常会导致住房需求以及消费能力的提高，进而推动商品住宅价格的上涨。单位面积房屋竣工造价(lnhc)的上涨，会导致住宅建造成本提高，成本的上涨必然会导致价格上涨。此外建造成本上涨还会影响开发商的住宅供应量，按照供需平衡理论，供应量的减少会导致价格的上涨。这些都与前文的理论分析结果相一致，但是关于商品住宅的投资完成额(lnpiv)，与理论分析有所差异，固定效应结果下的系数是正的，但是在分位数回归下的结果却是负的，符合前文的理论分析，所有这有可能是模型不同而带来的差异。

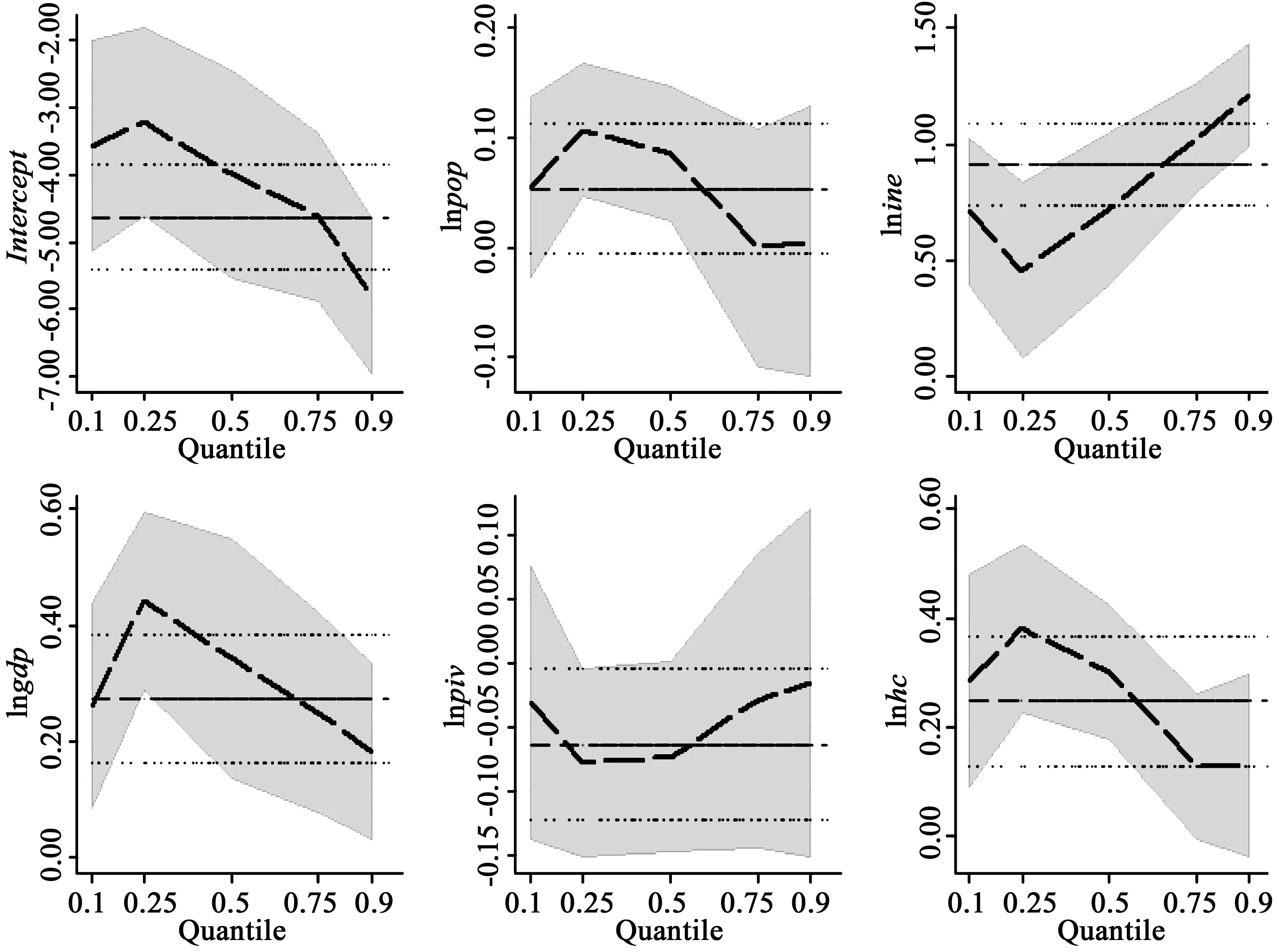
图2 各自变量随分位点变动图

第二，表中第(2)至第(6)列呈现的是分位数回归中不同分位点的估计结果。观察总人口(lnpop)在各分位点的回归结果可以看出，总人口的估计系数只有在0.25和0.5这两个分位点上是显著的，分别为0.107和0.085，这表明总人口只对中低房价和中等房价产生显著正向影响，而对低房价、中高房价和高房价是没有影响的。从某个角度而言，这同时也表明了我国住房的特殊性，它并不能完全等同于普通商品，人口增加导致的需求增加并不能完全影响到房价。在中低和中等房价的城市，相对而言，居民拥有与之相匹配的购买能力，因此这种情况下人口的增加会导致住宅有效需求增加；而对于中高房价甚至是高房价的城市，由于居民的承受能力有限，通常只有部分的较高收入者才是其真正的需求者，所以总人口的增加并不一定会导致这部分城市住宅的有效需求上涨，因此也不会影响其价格。

第三，观察人均可支配收入(lninc)在各分位点的回归结果可以看出，其在各分位点的系数为正且都通过了1%显著性水平下的统计检验，这表明整体而言人均可支配收入对商品住宅价格拥有绝对的正向影响。从低房价到中等房价再到高房价，其估计系数从0.713、0.457、0.724、1.027变动至1.211，可以看出人均可支配收入对商品住宅价格影响较大，且大体呈现一个上升的趋势。人均可支配收入对高房价的影响较之于低房价更大，从另一方面也说明了在我国高房价的城市对于购买者的收入要求更高，收入高者会更倾向于也更有能力在房价高的城市购买住房。

第四，观察人均GDP(lngdp)在各个分位点的回归结果可以看出，人均GDP在各分位点上的系数均为正，且在一定的显著性水平下显著。这表明人均GDP无论是对低房价还是高房价都有明显的正向推动作用，其估计系数从0.262、0.442、0.343、0.250变动至0.183，大体上呈现出先上升后下降的趋势，这与张所地(2015)的研究结果相似，即在我国城市房价上涨的过程中，人均GDP对房价的影响也越来越小。

第五，观察商品住宅投资完成额(lnpiv)在各分位点的回归结果可以看出，其只有在0.25和0.5这两个分位点上是显著的，且回归系数是负的，分别为－0.077和－0.073。这与固定效应的结果相反，与本文之前的理论分析相一致，即商品住宅的投资完成额增加，代表着住宅供应量的增加，按照供需平衡理论，这将会导致住宅价格的下降。但住宅不可等同于普通商品，对于高房价的城市，住宅的投资完成额对其住宅价格并不产生影响。换言之，住宅价格上涨，供应量增加，也许会导致住宅库存量增加，却不一定会导致住宅价格下降。

第六，观察单位面积房屋竣工造价(lnhc)在各分位点的回归结果可以看出，房屋竣工造价的回归系数在0.1，0.25，0.5分位点上是显著的，分别为0.284、0.381和0.301，而在0.75和0.9分位点上表现得不显著，这表明我国大中城市的房价并非单纯的是由房屋竣工造价所构成的。在房价相对较低的城市，住宅建造成本有一定的影响，而对于那些房价较高的城市，建造成本已经不是住宅价格的主要影响因素了。比如北京上海这样的一线城市，其住宅的建造成本并不会比南京等这样的二线城市高出多少，但两者房价却相差很多。所以在房价上涨的过程中，房屋竣工造价的影响来越小。

5 结论与建议

本文选取2005－2014年全国35个大中城市的面板数据，利用面板数据分位数回归的方法进行实证分析并与面板数据固定效应模型进行了对比，研究结果表明:在房地产市场研究中，应用面板数据分位数回归可以得到比固定效应模型更丰富的有关房价影响因素对房价影响效应的新知识。

在固定效应模型中，除了人均GDP，其他所有的变量包括总人口、人均可支配收入、商品住宅投资完成额以及单位面积房屋竣工造价都对商品住宅平均销售价格表现出显著的正向影响。其中人均可支配收入(lninc)的推动作用最大，人均可支配收入平均每增加1%，就会导致商品住宅的平均销售价格上涨40.9%。

面板数据分位数回归分析表明，人均可支配收入(lninc)和人均GDP(lngdp)在各分位点上的系数均为正且在一定的显著性水平下显著，并且人均可支配收入大体上呈现出一种上升的趋势，而人均GDP则呈现出下降的趋势。换言之，在我国城市房价上涨的过程中人均可支配收入对房价的正向推动作用越来越大，相反人均GDP的推动则越来越小。观察它们各系数值也可以发现，人均可支配收入对商品住宅平均销售价格的影响要远远大于人均GDP，且对高房价的影响系数甚至达到了1.211，即高房价城市的人均可支配收入每增加1个百分点，其房价就要增加121.1%。总人口(lnpop)在0.25和0.5这两个分位点上对商品住宅平均销售价格有显著的正向影响。当房价较高时，总人口的增加并不一定会导致有效需求的增加，因而不会对其产生重要影响。相反，商品住宅投资完成额(lnpiv)在0.25和0.5这两个分位点上对商品住宅平均销售价格呈现出显著的负向影响，这与固定效应的结果相反却与本文供给需求的理论分析保持一致。关于单位面积房屋竣工造价(lnhc)，其在0.75和0.9这样的高分位点上不显著，这就说明城市的高房价主要并不是由建造成本引起的。

根据本文的研究结果，我们提出如下政策建议:首先，由于收入在我国城市房价上涨的过程中起着至关重要的作用，因此在确保收入正常稳定上涨的同时，要抑制一部分高收入人群对住宅的需求，尤其是投资投机需求。同时要适当增加城市住宅的供应量，调整住宅供应结构，以缓解收入增加带来需求增加从而导致的房价过快上涨的现象。其次，对于一些房价较低的落后城市，政府应该大力发展经济，努力推进产业转型，提供更多的就业机会，提高居民的收入水平，增强居民的购买能力。再次，政府要增加保障性住房的供给，完善住房保障制度，以确保低收入者的住宅需求尤其是在房价较高的城市。积极建设与低收入人群住房需求相匹配的保障性住房，加快完善准入退出机制，加强住房保障监管。最后，由于各影响因素对不同分位点上的房价推动作用不一样。因此，房价各异的城市在制定房地产调控政策时应该因地制宜，即要充分考虑不同城市的实际情况如城市的经济发展状况、人均收入水平、住宅的开发程度等，从而制定出适合自身房地产市场健康发展的调控政策。例如2016年国庆前后至今各城市出台的调控政策，虽然都是以限贷限购为主，但不同城市政策出台的时间、次数、调控力度、具体的调控细则却不尽相同。这就表明即使是同样的政策，不同的城市出台的时间以及其实施力度都可以根据自身的情况具体落实，以达到更好的调控效果。

参考文献:

[1]张立新，姜吉坤，温海珍.基于特征价格模型的商品住宅价格评估方法应用[J].统计与决策，2010(21):157－159.

[2]刘在军.国内重点城市商品住宅价格影响因素实证研究[J].经济纵横，2010(14):112－114.

[3]张晶，杨萍.中美利率调控政策与房地产价格走势的实证分析[J].山东财政学院学报，2012(1):108－115.

[4]廖阳，焦成才.基于面板数据模型的商品住宅价格上涨作用机理及实证研究——以西部地区7个中心城市为例[J]城市发展与研究，2012，19(2):142－144.

[5]王泳茹.房地产市场供给与需求对房价的影响[J].统计与决策，2015(24):151－153.

[6]李顺毅.房价如何影响消费对经济增长的贡献——基于分位数回归的实证分析[J].消费经济，2011(3):3－6.

[7]罗玉波.房价影响因素分析:分位数回归方法[J].统计与决策，2011(6):158－159.

[8]林勇，吴甜甜.中国房价对城镇居民消费影响的异质性分析——基于311个城市的面板分位数回归[J].消费经济，2015(3):27－32.

[9]张所地，范新英.基于面板分位数回归模型的收入、利率对房价的影响关系研究[J].数理统计与管理，2015(6):1057－1065.

[10]林海波，梁艳，毛程连.房价和知识移民吸引是两难吗?——基于大中城市面板数据的分位数实证研究[J].人口与经济，2016(1):10－18.

[11]李群峰.基于分位数回归的面板数据模型估计方法[J].统计与决策，2011(17):24－26.

[12]谢旦杏，林雄斌.城市住房价格时空间特征及其影响因素研究[J].经济地理，2014(4):70－77.

[13]刘降斌，李亮亮.房地产价格影响因素的实证研究——基于我国各省的面板数据分析[J].经济研究导刊，2014(5):21－22.

[14]戴学珍，马娜.供需因素对城市商品住宅价格的影响及其空间分布[J].城市发展研究，2010(10):46－49.

[15]吴群，高慧琼.供求关系对大都市商品住宅价格作用机理的分析——以南京市为例[J].中国土地科学，2006(2):51－56.

[16]张凌，温海珍，贾生华.中国沿海和内陆城市住房价格波动差异与动力因素[J].中国土地科学，2011(3):77－84.

[17]丁军.北京、上海、深圳房地产价格的影响因素比较研究[J].中国房地产，2016(36):28－35.

Analysis of Commercial Housing Price Influencing Factors Based on Panel Data Quantile Regression

ZHAO Qiang，CAO Weiting
(School of Public Management，Nanjing University of Finance and Economics，Nanjing210023，China)

This paper firstly constructs the panel data of China 35 large and medium cities from 2005 to 2014 and then analyzes the influencing factors of real estate prices based on supply and demand theory and quantile regression method.The results show that the coefficients of disposable per capita income and per capita GDP are significantly positive in every quantile；the disposable per capita income presents an upward trend in every quantile while the per capita GDP presents a downward trend.The total population has a significant positive impact on the average commercial housing selling prices at 0.25 and 0.5 quantiles.On the contrary，the amount of commercial housing investment presents a significant negative impact at 0.25 and 0.5 quantiles while the housing completion cost per unit area presents no significant impact.Among all the influencing factors，the impact of disposable per capita income on housing price is largest while its impact on high housing price is greater than that on low housing price，which indicates that the cities with high housing prices require the buyers to earn a higher income.

house price；panel data； quantile regression； supply and demand theory

F293.3

A

2095－929X(2017)05－0061－09

(责任编辑刘小平)

2017－07－06

赵强，男，山西长治人，博士，南京财经大学公共管理学院副教授，研究方向:政府改革和创新；曹炜婷，女，江苏南通人，南京财经大学公共管理学院硕士生，研究方向:房地产市场与政策，Email:1445136575＠qq.com。